Использование пифагоровых троек чисел при изучении математики

Использование пифагоровых троек при изучении математики.

Использование рациональных вычислений является неотъемлемой частью урока математики. Это позволяет не только рационально использовать время урока, но и развивать у детей память, логическое мышление, способность видеть и развивать числовые закономерности.

Изучая в 8 классе теорему Пифагора, учитель знакомит учеников и с теоремой, обратной теореме Пифагора. В результате этого и вводится понятие «пифагоровых троек чисел». Работая в старших классах, я заметила, что их можно активно использовать не только при решении геометрических задач (нахождение катетов и гипотенузы в прямоугольном треугольнике, диагонали в прямоугольнике, расстояния от оси цилиндра до секущей плоскости, высоты в пирамиде и т.д.), но и в тригонометрии, после чего стала специально обучать учащихся применять их.

Пифагоровых троек существует бесконечное множество, но чаще всего используются следующие:   3,4,5     5,12,13    8,15,17   7,24,25   9,40,41   20,21,29    12,35,37.   Общий вид пифагоровых троек чисел :

Рассмотрим некоторые примеры использования пифагоровых троек чисел при изучении тригонометрии.

Пример 1.

Используя тройку: 8,15,17,  мы сразу находим   (ведь основное тригонометрическое тождество   есть не что иное, как теорема Пифагора.

Пример 2.

Вычислить

=

Можно заметить, что здесь снова «работает» пифагорова тройка чисел : 5,12,13,  что позволяет устно выполнять такие задания:

Пример 3.

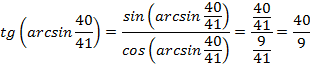
Пример 4.

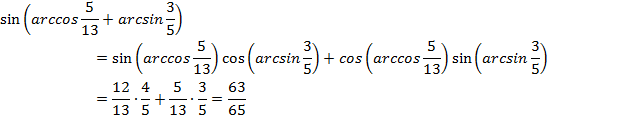
Пример 5.

Решить уравнение:

Это уравнение решается методом введения  вспомогательного угла.

Решая это уравнение, мы делили на  , а значит снова можно использовать пифагоровы тройки чисел и решать такие уравнения устно.

Например:

   (тройка: 8, 15, 17)

Или   

    (тройка: 20, 21, 29)

Пример 6.

Найти множество значений функции:

        (тройка: 7, 24, 25)

Таким образом множество значений функции  будет равно

И для функции

Своим исследованием я хотела показать, что использование пифагоровых троек позволяет устно решать некоторые типы геометрических задач, тригонометрических заданий, очень экономит время при решении подобных заданий, а значит позволит  потратить время на экзамене, в том числе и ЕГЭ, на более сложные задания.

Буду рада, если мое исследование, которое я провела уже более 10 лет тому назад, будет полезно для работы коллег.