ИСПОЛЬЗОВАНИЕ СВОЙСТВ СТЕПЕНИ С ЦЕЛЫМ

Использование свойств степени
с целым показателем для нахождения
значений выражений

Цели: изучить свойства степени с целым показателем; формировать умение применять данные свойства для нахождения значения выражения.

Ход урока

I. Организационный момент.

II. Устная работа.

– Вычислите:

а) 5^–3;                   б) 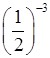;                 в) (–11)^–2;                  г) ;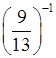    

д) (–3)^–2;              е) 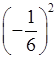;                ж) 2^–5;             з) ;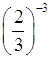

и) (–3)⁴;                к) .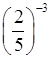

III. Объяснение нового материала.

Объяснение проводить по следующей схеме:

1. А к т у а л и з а ц и я   з н а н и й.

Вспомнить свойства степени с натуральным показателем и продемонстрировать их применение для преобразования и нахождения значений выражений.

2³ · 2² = 2^{3 + 2} = 2⁵ = 32;

3⁴ : 3² = 3^{4 – 2} = 3² = 9;

(2²)³ = 2^{2 · 3} = 2⁶ = 64;

(3 · 4)³ = 3³ · 4³ = 27 · 64 = 1728;

.

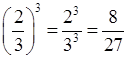2. С о о б щ и т ь  учащимся, что все рассмотренные свойства распространяются и на степени с любым целым показателем. Предполагаем, что основание степени не равно нулю.

На доску выносится запись:

Доказательство утверждений можно рассмотреть по учебнику на с. 207.

3. П р и в е с т и   п р и м е р ы, показывающие применение свойств степени с целым показателем для нахождения значения выражения (с. 207–208 учебника, примеры 1–3).

IV. Формирование умений и навыков.

На этом уроке необходимо начать формирование у учащихся следующих умений:

– непосредственно применять свойства степени с целым показателем для нахождения значения выражений;

– преобразование выражения в степень с «нужным» основанием для рационального применения свойств степени с целым показателем;

– упрощать выражения, используя свойства степени с целым показателем.

1. № 985.

Р е ш е н и е

а) 3^–4 · 3⁶ = 3^{–4 + 6} = 3² = 9;

б) 2⁴ · 2^–3 = 2^{4 – 3} = 2;

в) ;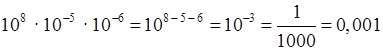

г) ;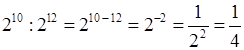

д) 5^–3 : 5^–3 = 5^{–3 – (–3)} = 5⁰ = 1;

е) 3^–4 : 3 = 3^{–4 – 1} = 3^–5 = ;

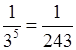ж) (2^–4)^–1 = 2^{–4 · (–1)} = 2⁴ = 16;

з) (5²)^–2 · 5³ = 5^–4 · 5³ = 5^{–4 + 3} = 5^–1 = ;

и) 3^–4 · (3^–2)^–4 = 3^–4 · 3⁸ = 3^{–4 + 8} = 3⁴ = 81.

2. № 987, № 988 – самостоятельное решение, два ученика работают у доски.

№ 989.

Р е ш е н и е

а)  = 3³ = 27;

б) ;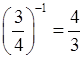

в) 0,01^–2 = 100² = 10000;

г) ;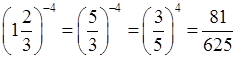

д) 0,002^–1 =  = 500;

е) .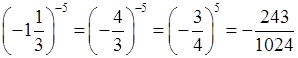

3. № 990, № 992.

Р е ш е н и е

№ 990.

а) ;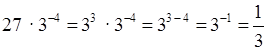

б) ;

в) ;

г) .

№ 992.

а) 5^т · 5^{т + 1} · 5^{1 – т} = 5^{т + т + 1 + 1 – т} = 5^{т + 2};

б) (5^т)² · (5^–3)^т = 5^2т · 5^–3т = 5^{2т – 3т} = 5^–т;

в) 625 : 5^{4т – 2} = 5⁴ : 5^{4т – 2} = 5^{4 – 4т + 2} = 5^{6 – 4т}.

4. № 993.

При выполнении этого упражнения учащиеся должны сами определить в виде степени, с каким основанием им удобно и необходимо представить выражение.

Р е ш е н и е

а) 8^–2 · 4³ = (2³)^–2 · (2²)³ = 2^–6 · 2⁶ = 2⁰ = 1;

б) 9^–6 · 27⁵ = (3²)^–6 · (3³)⁵ = 3^–12 · 3¹⁵ = 3^{–12 + 15} = 3³ = 27;

в) 10⁰ : 10^–3 = 10^{0 + 3} = 10³ = 1000;

г) ;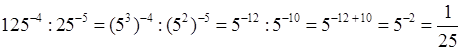

д) 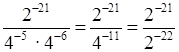 = 2^{–21 + 22} = 2;

е) 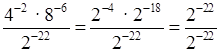 = 1;

ж) ;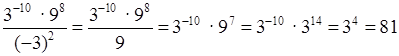

з) .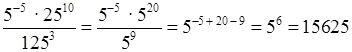

5. Сильным в учебе ученикам можно предложить для решения задание повышенной трудности.

№ 995.

Р е ш е н и е

а) 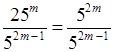 = 5^{2m – 2m + 1} = 5;

б) .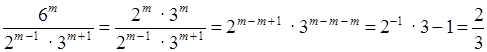

V. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Сформулируйте правила умножения и деления степеней с одинаковым основанием.

– Сформулируйте правило возведения в целую степень произведения и дроби.

– Сформулируйте правило возведения степени в степень.

Домашнее задание: № 986, № 991, № 994, № 1072.