Использование устных упражнений при изучении нового материала на уроках математики

Использование устных упражнений при изучении нового материала

 

Одной из эффективных форм организации коллективной и индивидуальной самостоятельной работы учащихся на уроках математики является систематическое выполнение устных упражнений на всех этапах обучения. Учитель должен ориентироваться на то, что, выполняя устные упражнения, учащиеся не только получают вычислительные навыки, а прежде всего, закрепляют теоретические знания, тренируют внимание и память.

Устные упражнения можно разделить на следующие виды:[3]

1. Условие упражнения воспринимается на слух, и после его выполнения ученики, ничего не записывая, сообщают результат.

2. Ученики читают условие упражнения (из учебника или доски), а решают задачу устно.

3. Учащиеся, рассмотрев рисунок и краткое условие задачи по геометрии, устно находят все необходимые соотношения между элементами изображенной фигуры и дают ответ.

4. По условию задачи ученики составляют соответствующий схематический рисунок геометрической фигуры или графика функции, или краткое условие текстовой задачи, а решения выполняют без записей.

Ученикам с начальным уровнем знаний можно предложить повторить решения задач, которые предварительно были рассмотрены в классе. Такой дифференцированный подход способствует мобилизации внимания и побуждает к активному участию в работе не только сильных, но и слабых, рассеянных учеников.

С помощью устных упражнений по геометрии на готовых чертежах решаются следующие дидактические задачи.

1. Формирование навыков применять соответствующие теоремы к решению задач.

2. Усвоение теоретических знаний по текущему материалу.

3. Организация учебной самостоятельной работы учащихся в процессе решения задач.

4. Развитие речи учащихся.

Устные упражнения по геометрии на готовых рисунках помогают сэкономить время, увеличить объем материала, который рассматривается на уроке, повысить эффективность урока, поскольку не тратится время на выполнение чертежа.

Пример 1. Использования устных упражнений на этапе актуализации знаний (рисунок 1).

 

 

 

 

 

 

 

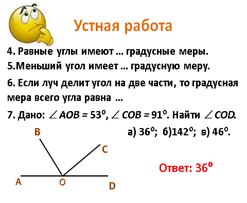
Рисунок 1. Решение задач по готовым чертежам

Таким образом, устные упражнения имеют, разное дидактическое назначение, их можно разделить на следующие три группы:  упражнения для актуализации опорных знаний; упражнения для восприятия и сознательного осмысления материала; упражнения на применение приобретенных знаний.

Упражнения первой группы учитель может использовать перед объяснением нового материала, их можно считать подготовкой к восприятию теоретического материала, они облегчают изучение новых понятий, утверждений, свойств.

Округление десятичных дробей

1. Какие из приведенных величин могут быть точными, а какие приближенными?

а) В школьной библиотеке 5000 книг;

б) в классе 32 ученика;

в) расстояние от Запорожья до Бердянска 200 км;

г) длина спортзала 20 м;

д) в коробке 12 карандашей.

2. Между какими соседними натуральными числами стоит каждая из дробей: 5,97; 1,03; 132,2; 8,75?

3. Округлите:

а) до десятков: 23; 15; 841; 1078;

б) до сотен: 647; 8739; 15981; 986.

Упражнения второй группы способствуют глубокому осознанию изученного материала, помогают учащимся усвоить ту или иную тему. Такие упражнения целесообразно использовать после объяснения нового материала, когда ученик устал и можно поработать устно. Одновременно учитель имеет возможность проверить глубину усвоения нового материала.

Пример 2. Упражнения на восприятие и осмысление нового материала

1. Прочитайте запись и назовите, к какому разряду относятся округленные числа:

а) 9,56927 = 9,5693; б) 0,378102 = 0,4;

в) 12,3631 = 12,36; г) 10,1287 = 10,129;

д) 18,327 = 18; е) 7,021 = 7,0.

2. Округлите:

а) до десятых: 17,25; 0,118; 35,579;

б) до десятков: 11,2; 27,96; 340,8;

в) до сотых: 3,028; 317,834; 112,5018;

г) до сотен: 162,3; 701,79; 5337,325.

Упражнения третьей группы дают возможность применять полученные знания. Выполнение таких упражнений способствует формированию умений и навыков, развивает логическое мышление, творческие способности.

Пример 3. Упражнения на применение полученных знаний

1. Какую цифру можно подставить вместо звездочки, чтобы было верным приближенное равенство?

а) 318 * = 318,6; 736,92 * = 736,92;

б) 23,1 * = 23,1; 736, * = 736;

в) 115,1 * = 115,2; 1 *, 2 = 20.

2. Число сначала округлили до десятков, затем до сотен, затем до тысячных. Всегда ли получим тот же результат, если округлим заданное число сразу до тысячных.

Готовясь к уроку, нужно тщательно отбирать материал, систематизировать его, продумывать переход от одной задачи к другой в целях обучения. При составлении системы задач и определения форм организации устной работы учитель должен учитывать индивидуальную подготовку учащихся, склонность и способность к устным вычислениям.

Необходимо понимать, что особенно большое значение имеют устные упражнения для формирование сознательного усвоения определений, законов и свойств арифметических действий, степеней, логарифмов и тому подобное. На простых, но разнообразных примерах ученики должны отрабатывать навыки использования свойств и законов, которые изучаются. Иногда бывает достаточно только изменить порядок действий, выполнить несколько простейших преобразований, опирающихся на определение, основные свойства математического понятия, и решение примера значительно упрощается. Учитель ставит ученикам следующие вопросы: как проще вычислить? нет ли более рационального пути решения? можно ли выполнить вычисления другим способом? существует ли более простой способ вычисления? какие свойства, законы «работают» при решении той или иной задачи? Учителю необходимо помнить, что фундаментом для дальнейшего усвоения любой темы являются сформированные вычислительные навыки. Формированию вычислительных навыков способствуют рациональные приемы вычисления. [17]

Пример 4. Способы быстрого сложения и вычитания натуральных чисел

Правило 1. Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо вычесть столько же единиц.

364 + 592 = 364 + (592 + 8) -8 = 364 + 600-8 = 964-8 = 956.

Правило 2. Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на столько же единиц, то сумма не изменится.

997 + 856 = (997 + 3) + (856-3) = 1000 + 853 = 1853.

Правило 3. Если вычитаемое увеличить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится.

1351-994 = (1351 + 6) - (994 + 6) = 1357-1000 = 357.

Правило 4. Если от суммы двух чисел отнять разницу этих цифр, то в результате получим вдвое меньшее число, то есть (а + b) - (а-b) = 2Ь.

(47 + 24) - (47-24) = 48.

Правило 5. Если к сумме двух чисел добавить их разницу, то в результате получим вдвое большее число, то есть (а + b) + (а-b) = 2а.

(65 + 34) + (65-34) = 130.

 

Подбор устных упражнений для обучающихся 5 классов.

Тема. Плоскость. Прямая. Луч.

Цель. Введение понятий плоскость, прямая, луч. Ученики должны распознавать прямые и лучи, изображать их с помощью линейки, описывать понятие луч.

Методические советы:

Следует отметить, что так же, как точка и отрезок, плоскость, прямая и луч - объекты абстрактные. С помощью рассматриваемых фигур, формируется представления у учащихся о бесконечности. Важно, чтобы ученики понимали, что в тетради можно изобразить только часть прямой или луча в виде отрезка.

Нередко ученики пытаются выяснить, состоит ли прямая из точек. Здесь лучше объяснить, что прямая есть целое, а точки могут принадлежать прямой либо не принадлежать ей.

Устные упражнения

1. Прочитайте число:

1) 5002030; 2) 7316000000; 3) 40040040004.

2. Удвойте число 26. Найдите половину числа 26. Утройте число 27.

Найдите треть числа 27.

3. Выполните действия

1) 64 + 36: 4; 3) 120-20-4;

2) (64+ 36): 4; 4) (120-20) • 4.

4. В 10 ч утра со станции отправился поезд со скоростью 60 км / ч. На каком расстоянии от станции будет поезд в 15 час того же дня, если двигаться все время с этой же скоростью и без остановок?

5. Сколько можно провести отрезков, концами которых будут:

1) 2 заданные точки; 2) 3 заданные точки; 3) 4 заданные точки?

6. Петя и Миша учатся в одной школе. Петя живет у одной конечной остановки автобуса, а Миша - у другой. Когда они едут в школу, то Петя выходит на пятой остановке, а Миша - на седьмой. Сколько всего остановок на этом маршруте?

 

Тема. Шкала. Координатный луч

Цель. Формирование у учащихся понятия координатный луч, ознакомление их с указанием натуральных чисел на луче. Ученики должны уметь приводить примеры шкал, описывать понятие координатный луч, изображать координатный луч и числа на координатном луче, читать шкалы.

Методические советы:

Желательно как наглядные пособия продемонстрировать на уроке любые приборы со шкалами (амперметр, вольтметр, штангенциркуль и т.п.).

Ученики должны понимать, что координатный луч - бесконечная шкала, для которой единичный отрезок можно выбрать произвольным образом.

Также следует объяснить, что положение точки на луче однозначно определяется ее координатой, и наоборот.

Устные упражнения

Выполните сложение:

1)                18 + 14; 2) 180 + .140; 3) 180 + 14; 4) 18 + 140.

2)                В пять одинаковых мешочков разложено поровну 10 кг конфет. Сколько нужно таких мешочков, чтобы разложить 30 кг конфет?

 

 

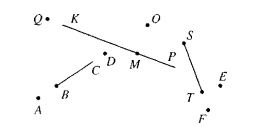
Рисунок 2.

Какие из точек А, В, Q, М, В, S, Т, Е, F, P (рис.2) относятся:

1) прямой КР;

2) лучу ВС;

3) отрезку SF?

Пересекаются ли изображенные лучи, прямые и отрезки на рис.3:

1) луч ВС и прямая КР;

2) прямая КР и отрезок SF;

3) луч ВС и отрезок SF?

Назовите  число, у которого цифра десятков в 3 раза больше цифры единиц и на 3 меньше цифры сотен. Сколько существует таких чисел?

 

Тема. Сравнение натуральных чисел

Цель. Формирование навыков сравнения натуральных чисел. Ученики должны описывать правила сравнения натуральных чисел, решать задачи, в которых предусмотрено сравнения натуральных чисел.

Методические советы:

В предыдущих классах учащиеся сравнивали натуральные числа. Поэтому эта тема не вызывает осложнений. Здесь новым является сравнение чисел с помощью координатного луча.

Нужно обратить внимание, что при сравнении величин их предварительно надо свести к одной единице измерения.

Устные упражнения

1. Какое из чисел 516 и 615 расположено на координатном луче левее?

2. Какое из чисел 405 и 504 расположено на координатном луче правее?

3. Какие натуральные числа лежат на координатном луче между числами 2508 и 2515?

4. Назовите 4 числа, которые лежат на координатном луче:

1) левее числа 16;

2) правее числа 101.

5. Сколько натуральных чисел расположено на координатном луче

правее числа: 1) 0;       2) 999 999 999 999?

6. В 8 ч термометр показывал температуру 4 ° С, а в 14 час - 12 ° С. чему равна цена деления этого термометра, если его столбик поднялся на 4 деления?

7.  Шесть одинаковых бочек вмещает 320 л воды. Сколько литров воды содержат 15 таких бочек?

 

1. Прочитайте запись:

1) 32> 16; 2) 17 <20; 3) 4 <5 <6; 4) 102 <106 <107.

2. Какие из приведенных неравенств являются правильными:

1) 483 <501, 2) 196> 202; 3) 994> 899; 4) 1024> 1204?

3. Назовите четырехзначное число, которое заканчивается цифрой 7 и меньше 1017.

4. Назовите число, которое делится на 5 и меньше 118.

5. Назовите наименьшее натуральное число, которое можно подставить вместо т в неравенство т> 734, чтобы это неравенство стало правильным.

6. Назовите наибольшее натуральное число, которое можно подставить вместо п в неравенство п <3108, чтобы это неравенство стало правильным.

7. Петя и Миша имели поровну денег. Петя купил 7 одинаковых тетрадей, а Миша - 15 таких тетрадей, и у него осталось на 2 р. 40 к. меньше денег, чем у Пети. Сколько стоит одна тетрадь?

 

1. Вычислите:

1) (27 + 13) -8; 3) (82-71) -6; 5) 63: (25 - 16);

2) (56-26) -9; 4) (128 53): 3; 6) 120: (26 + 14).

2. Известно, что 24 * 5> 2475. Какая из приведенных цифр может стоять вместо звездочки:

1) 0; 2) 4; 3) 8; 4) 7; 5) 9?

3. Какие цифры можно поставить вместо звездочек, чтобы было правильным неравенство (рассмотреть все возможные случаи):

1) 4002> * 997; 3) 25998 <25 ***;

2) 9004 <* 009; 4) 2001> 2 ***?

4. В номерах вместо одной или нескольких цифр поставили звездочки, можно ли утверждать, что:

1) 975 <97 * 5; 3) 999 <1 * 00; 5) 99 * 9 <99 * 9;

2) 5246 <52 * 6; 4) 9996 <999 *; 6) 1000> 9 **?

5. Количество воды в бочке ежеминутно удваивается. Бочку можно наполнить за 10 мин. Какая часть бочки наполнится за последнюю минуту? За сколько минут наполнится половина бочки?

6. В коробке лежат 5 красных и 3 зеленых карандаши. Наугад из нее вынимают  по одному карандашу. Сколько карандашей надо взять, чтобы среди них были, по крайней мере, два красных и один зеленый?

 

При составлении заданий для устной работы необходимо учитывать возрастные особенности детей. На уроках в среднем звене можно применить нестандартную запись устного счета, а также устный счет в виде соревнований, устный счет с элементами игровой деятельности.

Несмотря на позитивное содействие устной работы усвоению знаний, формированию умений и навыков, не следует чрезмерно ею увлекаться. Важно, чтобы устная работа была органически связана и сбалансирована с письменными видами работы на уроке. Проведение устной работы является одним из средств обучения математики, а не самоцель.