Использование заданий функциональной грамотности на уроках математики

Использование заданий функциональной грамотности

на уроках математики

    Современная система школьного образования переживает большие изменения в своей структуре, на передний план в данный момент выходят требования общества к выпускникам. Заказ общества - на всесторонне развитую личность, способную принимать нестандартные решения, умеющую анализировать, сопоставлять имеющуюся информацию, делать выводы и использовать творчески полученные знания.

       В новых обстоятельствах процесс обучения школьников должен быть ориентирован на развитие компетентностей, способствующих реализации концепции «образование через всю жизнь». В международном исследовании PISA (Programme for International Student Assessment) термин «функциональная математическая грамотность» означает «способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе».

       И несомненно, что новые требования предъявляются к преподаванию школьных предметов, и математики в частности. Я, как учитель, на уроках математики делаю акцент н формирование навыков приобретения критического мышления, в этом им могут помочь задания по формированию функциональной и читательской грамотности учащихся.

    Понятие «функциональная грамотность» предполагает владение умениями:

- выявлять проблемы, возникающие в окружающем мире, решаемые посредством матем. знаний,

- решать их, используя математические знания и методы,

- обосновывать принятые решения путем математических суждений,

- анализировать использованные методы решения,

- интерпретировать полученные результаты с учетом поставленной задачи.

     Для развития «функциональной  математической грамотности» мною используются разнообразные задания (задачи и кейсы). При отборе содержания заданий, учитываю основные темы традиционного школьного курса математики: числа, измерения, оценка, алгебра, функции, геометрия, вероятность, статистика, элементы теории чисел. В рамках этих тем значительное внимание уделяю ряду вопросов, имеющих высокую практическую значимость (измерение геометрических величин, оценка, проценты, масштаб, интерпретация диаграмм и графиков реальных зависимостей, вероятность, статистические показатели и др.).

     Математическая грамотность напрямую зависит от читательской грамотности, т.к. текст, ситуация и вопрос, только в совокупности они могут развивать умения не пересказа

прочитанного, а поиска и интерпретации информации. В этом смысле полное понимание текста зависит от умения найти необходимую информацию и извлечь ее из общего контекста, сформулировать общее понимание текста и представить собственную точку зрения о содержании и форме текстового сообщения (задачи).

Использую все виды текстов:                                                              

— «сплошные тексты», как правило, это художественные тексты;

— «несплошные тексты», которые содержат информационные единицы (таблицы, графики, диаграммы);

— «смешанные тексты», которые содержат вербальные и невербальные элементы;

— «составные тексты», они соединяют несколько текстов, различных не только по содержанию, но и по формату.

 Таких текстов  или нет  вообще или имеются в недостаточном количестве школьных учебников. Поэтому приходится использовать материалы сайтов и пособий по подготовке к ВПР и ГИА.

      В 5-м и 6-м классах считаю важным научить детей гибкому чтению на уроках математики. Задания к упражнениям по степени сложности могут быть разными:

· определять главное и второстепенное в тексте задачи;

· сопоставлять данные по тексту, соотнести их характеристики;

· уметь формулировать вопросы по данным задачи (текста);

· составлять задачи по схеме (рисунку), используя частичные данные;

· вычленять новую информацию из текста и сформировать ее главную мысль по отношению к тексту;

· развивать механизм формирования научной речи, умение грамотно выражать свои мысли;

   Одно из ведущих мест в «математической грамотности» отводится учебной задаче. Термин «учебная задача» - в широком понимании - это то, что выдвигается самим учеником для выполнения в процессе обучения в познавательных целях. Учебная задача часто рождается из проблемной ситуации, когда незнание сталкивается с чем-то новым, неизвестным, но решение учебной задачи состоит не в нахождении конкретного выхода, а в отыскании общего способа действия, принципа решения целого класса аналогичных задач. Учебная задача решается школьниками путем выполнения определенных действий: знаю – не знаю – хочу узнать.

   Типы учебных задач:

· задания, в которых имеются лишние данные;

· задания с противоречивыми данными;

· задания, в которых данных недостаточно для решения;

· многовариативные задания (имеют несколько вариантов решения).

Задача учителя по формированию новых компетенций при работе с учащимися

предполагает работу применения новых знаний, нового способа по выработанному алгоритму. Для этого я использую для решения ситуационные, практико-ориентированные задания, задачи открытого типа.

    Типы задач:

· Предметные задачи: в условии описывается предметная ситуация, для решения которой требуется установление и использование знаний конкретного учебного предмета, изучаемых на разных этапах и в разных его разделах; в ходе анализа условия необходимо «считать информацию», представленную в разных формах, сконструировать способ решения.

· Межпредметные задачи: в условии описана ситуация на языке одной из предметных областей с явным или неявным использованием языка другой предметной области. Для решения нужно применять знания из соответствующих областей; требуется исследование условия с точки зрения выделенных предметных областей, а также поиск недостающих данных, причем решение и ответ могут зависеть от исходных данных, выбранных (найденных) самими обучающимися.

· Практико-ориентированные задачи: в условии описана такая ситуация, с которой подросток встречается в повседневной своей жизненной практике. Для решения задачи нужно мобилизовать не только теоретические знания из конкретной или разных предметных областей, но и применить знания, приобретенные из повседневного опыта самого обучающегося. Данные в задаче должны быть взяты из реальной действительности.

· Ситуационные задачи: не связаны с непосредственным повседневным опытом обучающегося, но они помогают обучающимся увидеть и понять, как и где могут быть полезны ему в будущем знания из различных предметных областей. Решение ситуационных задач стимулирует развитие познавательной мотивации обучающихся, формируют способы переноса знания в широкий социально-культурный контекст.

  Например, в своей практике  использую задания для 5-6 классов.

Задача 1 «План» Прочитайте внимательно текст и выполните задание.

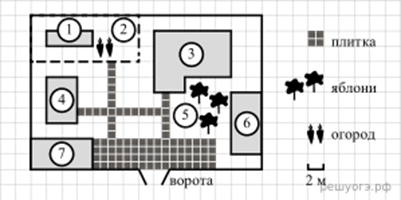На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок справа от ворот находится баня, а слева  — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.

Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.

Все дорожки внутри участка имеют ширину 1м и вымощены тротуарной плиткой размером1м × 1м

 Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.  К домохозяйству подведено электричество. Имеется магистральное газоснабжение.

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр.

Задача 2 «Геометрическая»

2.1. На карте показан путь Лены от дома до школы. Лена измерила длину каждого участка и подписала его. Используя рисунок, определите, длину пути (в м), если масштаб 1 см:10000 см

2.2. Найдите периметр прямоугольного участка земли, площадь которого равна 800м 2 и одна сторона в 2 раза больше другой. Ответ дайте в метрах.

2.3. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см 40 см?

2.4. Из четырёх деревянных досок длиной 90 см, шириной 55 см и толщиной 8 см склеили брусок, как показано на рисунке. Найдите объём этого бруска в куб. сантиметрах.

2.5. Изображённую на рисунке фигуру из кубиков поместили в коробку, имеющую форму прямоугольного параллелепипеда. Какое наибольшее количество таких же кубиков может поместиться в такой пустой коробке?

2.6. Найдите площадь клумбы без дорожки. Ответ дайте в квадратных метрах.

План местности разбит на квадраты. Сторона квадрата равна 1 м. На плане местности изображена клумба, разбитая на две части прямой дорожкой.

2.7. На плане, данном в условии, изобразите прямоугольную клумбу, площадь которой на 4 м² больше площади данной клумбы (без дорожки).

Задача 3 «Таблицы, диаграммы»

3.1.В каком году в Большом театре балет «Щелкунчик» шёл больше раз, чем в другие годы? На диаграмме показано, сколько раз в Большом театре шли балеты «Щелкунчик» и «Лебединое озеро» в течение пяти лет.

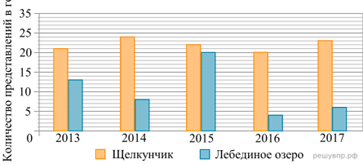
3.2. Сколько всего раз шёл балет «Лебединое озеро» в Большом театре в течение трёх лет,с 2013 по 2015г.? На диаграмме показ.,сколько раз в Большом театре шли балеты«Щелкунчик» и «Лебединое озеро»за 5лет.

3.3. В таблице показаны результаты работы четырёх принтеров. Сколько страниц в минуту печатает принтер с самой большой скоростью печати?

31.10.2024      ШМО учителей естественно- математ.дисциплин                  Учитель Митрофанова Н.В.