Исследовательская работа

Целинная средняя школа

филиал Муниципального бюджетного общеобразовательного учреждения

«Ключевская средняя образовательная школа № 2»

Ключевского района Алтайского края

 

 

Исследовательская работа

по дисциплине

 «Естественно – научное»

(математика)

«Математика и поэзия»

 

Автор работы: Котов

Даниил Максимович

ученик 7 класса

Целинная СОШ  филиал МБОУ «КСОШ № 2»

Ключевского района

Алтайского края

пос. Целинный,

ул. Спортивная 22

Научный руководитель:

Карпучева Ирина Владимировна

 

 

пос. Целинный 2019

 

Содержание

Введение. 3

Глава 1. Теоретическая часть работы. 5

1.1  Великие математики и поэты..…………………………………………..5

1.2   Цифровая поэзия.……………………………………………………….10

1.3   Математические правила: в стихах или прозе?....................................15

Глава 2. Практическая часть работы..……………………………………...19

2.1  Стихи в цифрах и без единого слова. 19

2.2  Рифмованные правила  и определения по математике..…….….....….21

Заключение. 22

Литература. 24

Приложения..………………………………………………………………..26

 

 

Введение

Актуальность работы:

Математика всегда сопровождала человека в жизни. Однако отношение людей к слову «математика» двоякое: одни почти ненавидят и считают, что она не пригодится в жизни, другие испытывают радостное чувство от решения трудной задачи. Ясно одно: равнодушных к математике нет.

Математика есть часть общего образования. Ныне ни одна область человеческой деятельности не может обходиться без математики – как без конкретных математических знаний, так и интеллектуальных качеств, развивающихся в ходе овладения этой учебной дисциплиной. Огромно значение математического образования в воспитании всесторонне развитой личности, ведь оно способствует: овладению конкретными знаниями, необходимыми для ориентации в современном мире; приобретению навыков логического и алгоритмического мышления; развитию воображения и интуиции; формированию мировоззрения; формированию нравственных черт; воспитанию способности к эстетическому восприятию мира; обогащению запаса историко-научных знаний.

Математическое образование является неотъемлемой частью гуманитарного образования в широком понимании этого слова, существенным элементом формирования личности.

Многим известна фраза «Физики-лирики», подчеркивающая, насколько отличаются точные науки, в частности, математика, от гуманитарных наук. Однако в последнее время все чаще можно услышать, что математика – это язык, наш второй язык, который нельзя не учить. «Первый язык – родной, второй – математический, а потом идет иностранный язык. То есть математику нужно учить для того, чтобы понимать существующие тексты любого рода. Не будешь знать математику, не поймешь и половины сюжетов, не уяснишь, что написано или нарисовано» – говорил в интервью журналу «Математика в школе» вице-президент Российской академии образования, доктор педагогических наук Болотов Виктор Александрович. На языке математики говорят не только все точные науки. Математическое языковедение – новая наука, связанная с машинным переводом, стихами, сочиненными машинами, расшифровкой языков исчезнувших народов.

Математика неисчерпаема и многозначна. Математика достойна того, чтобы о ней слагали стихи и пели песни, ведь и она обогащает великий и могучий русский язык. Трудно представить литературные произведения, тексты песен без цифр, чисел, числительных. А сколько загадок, поговорок, пословиц потеряли бы свой смысл, не будь в их содержании цифр и чисел!

Поэзия математики представляет своего рода сплав науки и искусства. 

В 90 – е годы прошлого века начали говорить о необходимости сочетать серьезное естественнонаучное и техническое образование с гуманитарным. Сейчас все большую популярность завоевывает такая, на первый взгляд, парадоксальная идея: лучшее усвоение знаковой информации, которую несет математика, происходит при помощи лучшего усвоения образной информации – музыки, поэзии, фольклора, живописи.

Избежать односторонности в изучении математики может помочь широкое применение метода аналогии.

С помощью математико-гуманитарной аналогии можно перевести математику, ее правила, методы, проблемы, задачи, теоремы на язык гуманитарной культуры, на язык образов, символов и эмоций. В качестве исследования рассмотрим поэтические произведения: цифровую поэзию, рифмованные правила. Сквозь призму математических знаний, попытаемся найти то, что объединяет их с математикой (установить ассоциацию по схожести), интерпретировать математику языком поэзии.

 

Объект исследования: стихи поэтов, проявляющих интерес к математике, математические определения и правила.

 

Предмет исследования: для чего нужны цифровые стихи, рифмованные правила в математике.

 

Цель работы: доказать связь математики и поэзии, показать важность  использования правил в стихотворной форме на уроках математики для лучшего усвоения материала.

Задачи:

1.     установить связь между математикой и поэзией;

2.     выяснить появление цифровых стихов;

3.     выяснить, влияет ли заучивание стихов на развитие памяти;

4.     подобрать стихи поэтов для перевода в цифровые;

5.     подобрать изученные правила курса математики;

6.     сформулировать некоторые правила в стихотворной форме;

7.     сделать подборку рифмованных правил других авторов;

 

В процессе работы были использованы следующие методы научного исследования:

1.     сбор информации в литературных источниках и сети Интернет;

2.     анализ изученных правил курса математики;

3.     аналитический;

4.     обобщение.

Гипотеза: математика тесно связана с поэзией, а использование рифмованных математических правил способствует развитию памяти и лучшему усвоению материала.

 

Глава 1. Теоретическая часть работы

 

1.1  Великие математики в поэзии[1]

Математика и поэзия. Что роднит их?  Кажется, нет никакого смысла в связи математики и поэзии. Математика и поэзия. Слова, которые редко стоят рядом. Когда речь заходит о поэзии - чаще подразумеваются уроки литературы, музыки, изобразительного искусства. О математике же говорят, как о науке абстрактной и сухой. Разумеется, у этой науки свой особый язык: язык рассуждений и доказательств. Но это не означает, что в математике не найдется место поэзии.

Многие ученые, помимо своей научной деятельности, занимались чем-то еще. Как показывает история науки, еще со времен пифагорейцев выдающиеся математики увлекались поэзией и даже сами пробовали писать.  Большое математическое дарование нередко сочетается с проявлением творческого интереса к поэзии. Многие поэты и писатели все-таки являются математиками в душе и многим математикам свойственны поэтические таланты.

Женщина математик Софья Васильевна Ковалевская говорит о математике так: «Это наука, требующая наиболее фантазии, нельзя быть математиком, не будучи в то же время поэтом в душе».

Ковалевская внесла огромный вклад в развитие математической науки. Ее работы известны во всем мире, ее именем названа «теорема Коши-Ковалевской» и частный случай в задаче о вращении твердого тела вокруг неподвижной точки.

Она - великий математик, она - признанный писатель и поэт. Вся ее прекрасная жизнь есть образец служения науке. Могучий русский талант, настойчивость, постоянное стремление вперед, непрерывный многолетний труд – все до конца было отдано науке. История знает мало имен женщин, которые бы могли сравняться с русской ученой Софьей Васильевной Ковалевской.

Одним из крупнейших математиков, который был замечательным поэтом, является Омар Хайям.

Омар Хайям завершил построение геометрической теории кубических уравнений. В алгебре он построил классификацию кубических уравнений и дал их решения с помощью конических сечений.

Параллельно с занятиями наукой Хайям создавал свои четверостишия («Рубаи»).

Омар Хайям навсегда вошел в историю всемирной культуры не только как блестящий ученый - энциклопедист, но и как прекрасный поэт. Его мудрые лирические четверостишия, наполненные глубоким философским смыслом.

Рене Декарт ­ французский философ, математик, физик и физиолог. 
Вообще­ то он и начал свою творческую жизнь с поэзии и много работал в этом
жанре. Увековечил он себя в области математики и философии, а всё же его 
последней работой была пьеса в стихах. 

Гениальный русский ученый Михаил Васильевич Ломоносов является творцом идей новой науки во многих областях. Он величайший химик, физик, геолог и в то же время историк, языковед и даже поэт. Научная деятельность Ломоносова была весьма разносторонней и протекала в непрерывной борьбе за процветание самостоятельной русской науки (разработал проект Московского университета, впоследствии названного в его честь). Первый великий русский учёный-естествоиспытатель мирового уровня.

Великий русский ученый М.В. Ломоносов говорил о математике так: «Математику уже затем учить надо, что она ум в порядок приводит».

«У каждого свой исходный постулат, на котором построена его геометрия жизни. Нужно только пристальнее приглядеться к человеку, определить этот исходный постулат и тогда всё станет ясно, все поступки окажутся логически обоснованными. Можно даже наперёд предсказать, как поступит тот или иной человек». Так говорил Николай Иванович Лобачевский.

Лобачевский получил ряд ценных результатов в других разделах математики: так, в алгебре он разработал, метод приближённого решения уравнений, в математическом анализе получил ряд тонких теорем о тригонометрических рядах, уточнил понятие непрерывной функции, дал признак сходимости рядов и др. В разные годы он опубликовал несколько содержательных статей по алгебре, теории вероятностей, механике, физике, астрономии и проблемам образования.

В 1834 году Лобачевский рискнул опубликовать свое стихотворение «Разлив Волги при Казани».

Брюсов Валерий Яковлевич - русский поэт, прозаик, драматург, основоположник символизма, критик, переводчик, литературовед.

В.Я. Брюсов изучал статистические закономерности в произведениях поэзии. Он писал: «Математику как олицетворение рассудочности обычно противопоставляют поэзии, постигающей мир иными, не рассудочными средствами».

Михаил Юрьевич Лермонтов постоянно искал новую деятельность и никогда не отдавался весь тому высокому поэтическому творчеству, которое обессмертило его имя и которое, казалось, должно было поглотить его всецело. Постоянно меняя занятия, он со свойственной ему страстью, с полным увлечением отдавался новому делу.

Лермонтов был большим любителем математики и одно время исключительно занимался математикой, в своих вольных переездах из одного места службы в другое 
всегда возил с собой учебник математики. Однажды, он до поздней ночи сидел над решением какой-то математической задачи. Не решив ее, Лермонтов, измученный, заснул. Задачу эту он решил во сне.

Александр Сергеевич Пушкин.

Русский поэт, драматург и прозаик, заложивший основы русского реалистического направления, критик и теоретик литературы, историк, публицист; один из самых авторитетных литературных деятелей первой трети XIX века. 

Широко распространено мнение, что А.С.Пушкин был не совсем в ладах с математикой, что она не давалась ему с детства и поэтому он ее не любил. На самом деле, интересы Александра Сергеевича были разносторонними.

Вяземский П.А. писал о Пушкине, что тот был «страстен и к наукам естественным и особенно математическим, которые составляли значительнейший капитал его знаний, и были до конца любимым предметом его учебных занятий и глубоких исследований».

А.С.Пушкин был страстным игроком в карты. Возможно, что страсть Пушкина к картам являлась дополнительной причиной его повышенного интереса к теории вероятностей. Совпадение кульминационных моментов в произведениях прозы у Пушкина удивительно близкое с золотой пропорцией. Всматриваясь в математически 
строгие и точные композиции крупнейших пушкинских произведений, 
начинаешь по-настоящему понимать всю неслучайность пушкинского 
утверждения, что «вдохновение нужно в поэзии, как и в геометрии».  Размеры стихов распределены совсем не равномерно, выделяются предпочтительные и редко встречающиеся размеры. Проявляется вполне закономерная тенденция в творческой манере поэта, он явно предпочитает стихотворения, размер которых близок к числам ряда Фибоначчи. И это никак нельзя признать случайностью, игрой слепой вероятности. Наличие этих чисел выражает одну из фундаментальных закономерностей творческого метода поэта, его эстетические требования, чувство гармонии. Таким образом,  
прослеживается «странное сближение» Пушкина и математики.

 

1.2   Цифровая поэзия

Цифровая поэзия – стихи, записанные цифрами.

Цифровые стихи – числовые ритмические абстракции, звучащие как стихотворения.

Цифровые стихи обладают особым обаянием, ритмом и своеобразной энергетикой. 
Их обязательно надо читать с выражением и вслух. 
Цифровые стихи ближе к музыке, ведь ни там, ни там нет слов и готовых образов.

Дигитальная литература,  дигитальная поэзия (от англ. digital — цифровой) — совокупность литературных произведений, созданных с использованием компьютерных технологий таким образом, что без этих технологий такое произведение существовать не может.

Современный цифровой век принес нам новый вид поэзии — цифровые стихи. Вы можете удивиться: как это стихи в цифрах и без единого слова? Именно!

Цифровые стихи тем и отличаются от традиционных, что в них вместо слов зарифмованы различные цифры.

         Когда точно появился этот вид поэзии сказать трудно. Одни утверждают, что цифровые стихи появились благодаря креативу программистов, которые стремятся все оцифровать. Другие утверждают, что мода на стихи в числах пришла к нам с Запада в 90-е годы XX века. Третьи говорят, что баловались написанием веселых цифровых стихов еще в школе задолго до всеобщей компьютеризации. Тогда они назывались «дигитальными стихами» или «авральным стихотворчеством» и их написанием было увлечено огромное количество людей.

         В цифровой поэзии используют только числительные. А для экономии места так числами и записывают. Однако по форме это настоящие стихи. В цифровых стихотворениях сеть и рифма, и ритм, и размер. Единственное, что в них может отсутствовать — это смысл. Но в цифровой поэзии смысл далеко не главная составляющая, поэтому без него можно вполне обойтись. С одной стороны, они полностью абстрактны – практически всегда непонятно, о чём, собственно в них говорится. С другой стороны, в них хорошо чувствуются ритм и настроение автора. И этим цифровая поэзия похожа на музыку. Может быть,  именно  эту музыку цифр имел в виду знаменитый поэт Иосиф Бродский, когда однажды написал: «В цифрах есть нечто, чего в словах, даже крикнув их, нет».

Читать цифровые стихи надо вслух и с выражением. Достаточно произносить написанные числа и уловить ритм. Не стоит думать, что цифровые стихи примитивнее традиционных стихотворений. Стихи в числах разделяют на жанры, определяют размер и прочее. Бывают веселые цифровые стихи, грустные цифровые стихи, стихи классиков в числах и т.д.

Цифровые стихи обладают особым обаянием. Они намного ближе к музыке, нежели обычные стихотворения. Цифровые стихи развивают воображение, поскольку в них нет готовых, созданных поэтом, образов. Читателю дается полная свобода мысли. Поэтому цифровые стихи полезно читать вместе с детьми, так они научатся чувствовать ритм и разовьют воображение. Главное, почувствовать ритм.

Кстати, цифровые стихи — это прекрасная основа для постижения тонкостей теории стихосложения. Мелодичность стихотворения зависит от порядка чередования в нем ударных и безударных гласных. От того ударный или безударный первый слог зависит род стопы.

Всего существует пять стоп: ямб (1 — ударение на втором слоге), хорей (8 — первый слог ударный), дактиль (1000 — ударение на первом из трех слогов), амфибрахий (13 — ударение на втором из трех слогов) и анапест (50 — ударение на последнем из трех слогов).

Примеры

 

 

В. Маяковский 2 46 38 1  116 14 20 15 14 21 14 0 17...  2 46 38 1 116 14 20 15 14 21 14 0 17	В. Маяковский (Стихи о Советском паспорте)  Я волком бы выгрыз бюрократизм.  К мандатам почтения нету.  К любым чертям с матерями катись  любая бумажка. Но эту...  Я достаю из широких штанин Дубликат бесценного груза. Читайте, завидуйте, я — гражданин Советского Союза.
В.Маяковский 47 3 9 5 3 4 20 220 305 2 105 17 ?	В.Маяковский Крошка сын к отцу пришел,  и спросила кроха:  - Что такое хорошо  и что такое плохо?
А.С. Пушкин 17 30 29 128 35 133 149 516 2 105 5020 6 108 15 30 47 127 5 2 08 2000 0 27	А.С. Пушкин (из поэмы "Руслан и Людмила") У лукоморья дуб зеленый; Златая цепь на дубе том: И днем и ночью кот ученый Всё ходит по цепи кругом; Идёт направо - песнь заводит, Налево - сказку говорит. Там чудеса: там леший бродит, Русалка на ветвях сидит;
С. Есенин 45 132 17 27 16 32 2 4 10 220 340 5 4 2 18 7 4 8 915 45 327 6 48 28 3 4 5	С. Есенин (Письмо матери) Ты жива еще, моя старушка? Жив и я. Привет тебе, привет! Пусть струится над твоей избушкой Тот вечерний несказанный свет. Пишут мне, что ты, тая тревогу, Загрустила шибко обо мне, Что ты часто ходишь на дорогу В старомодном ветхом шушуне.
Жили у бабуси… 40 38 2 128 1 10 1 10 2 128	Жили у бабуси… Жили у бабуси  Два весёлых гуся,  Один - серый, другой - белый,  Два весёлых гуся.
Гимн Советского Союза 16 13 12 4 17 15 14 2 13 16 4 12 15 14 132!	Гимн Советского Союза Союз нерушимый  республик свободных  Сплотила навеки Великая Русь. Да здравствует созданный  волей народов Единый, могучий Советский Союз!
А.Фет 40 18 42 06 20 8 20 219 300 40 6	А.Фет Ласточки пропали,  А вчера зарей  Всё грачи летали  Да как сеть мелькали  Вон над той горой
Считалка 1 40 9 3 15 30 8 2 17 20 10 60 7 13 50	Считалка 1 Вышел месяц из тумана,  Вынул ножик из кармана.  Буду резать, буду бить – Всё равно тебе водить.
Частушки 1 2 4 37 42 15 230 5 6 7 29 20	Частушки 1
Частушки 2 10 40 5 15  1.000.000 14, 39 8 20,  25 11…	Частушки 2

 

 

            У цифровых стихов ещё много возможностей. Например, можно использовать цифры,  перемешанные  со словами, знаки математических действий (+, -, : и т.д.) и разные поэтические хитрости. С помощью таких стихов запоминают телефонные номера, правила или шифруют дату кого-то важного события.

 

Примеры

 

Телефонный номер 288 – 53 – 27 поможет запомнить легче стишок:

Два весёлых великана

Пьют «Тархуна» два стакана

В нем использованы слова, начинающиеся на те же буквы, что очередная цифра в номере телефона (два – 2, весёлых – 8(восемь), великана – 8(восемь), пьют – 5(пять), тархуна – 3(три), два – 2, стакана-7(семь)).

 

1.3   Математические правила: в стихах или прозе?

 

В математике встречаются понятия, правила, запоминание которых даже осознанное происходит тяжело. А между тем известно, что одна удачно подобранная фраза, различные мнемонические приёмы позволяют легко запомнить то, что требует усиленной работы памяти. Школьники быстро и легко запоминают рифмованные строчки правил и определений.

Карл Вейерштрасс утверждал, что «нельзя быть математиком, не будучи одновременно поэтом в душе». А С.В. Образцов уверял: «Человек не может понимать окружающий его мир только логикой мозга, он должен ощутить его логикой сердца, т.е. эмоцией».

В 7-м классе на уроках геометрии вводятся понятия “медиана, биссектриса и высота треугольника”, но только биссектрису знает прочно не одно поколение школьников и их родственников. Почему? Всё очень просто! Потому, что «биссектриса – это крыса, которая бегает по углам и делит угол пополам». А нельзя ли придумать что-нибудь аналогичное? И вот появляется «медиана – обезьяна, «высота похожа на кота», которые если ещё и сопроводить забавными картинками с «геометрическими» зверятами, то данные понятия прочно засядут и в головах и в душах учащихся.

В рамках исследовательской работы среди учащихся школы было проведено анкетирование (приняли участие 60 респондентов). (Приложение А, Б).

Результаты опроса (2 респондента решили, что математические правила «хороши» и в стихах, и в прозе):

.

 

 

Математические правила
в стихах	в прозе
66 – 74%	16 – 16%

 

 

 

 

 

 

 

 

 

 

 

 

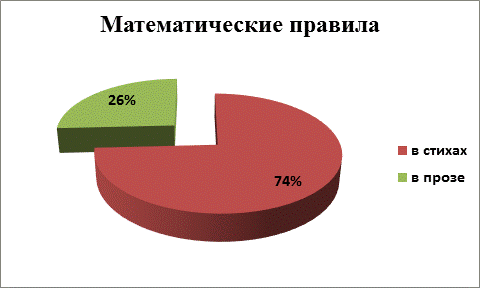
           Чаще всего рифмованные правила используются на уроках математики и русского языка.

 

           Математические правила в стихах

 

МЕДИАНА – обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас.

 

ВЫСОТА похожа на кота,
Который, выгнув спину,
И под прямым углом 
Соединит вершину 
И сторону хвостом.

 

Вам стишок читаю новый,
Кто запомнит – молодец.
У ОТРЕЗОЧКА любого 
Есть начало и конец.

 

Вдруг на небе из-за серых тёмных туч
Показался долгожданный солнца ЛУЧ, 
У которого, открою вам секрет,
Есть начало, а конца, ребята, нет

Всё, что в жизни нашей свято,
Мы не вправе отрицать.

У ПРЯМОЙ же нет, ребята,
Ни начала, ни конца.

У человека два плеча,
А в сутках день да ночка.

УГЛОМ назвали два луча –
С началом в общей точке.
Там, где труд не знает лени,
Хорошо идут дела!

 

Там, где числа и деленья,
Получается ШКАЛА.
Длина каждого деления – 
Единица измерения.

 

ДРОБЬ ОТ ЧИСЛА хотим найти,
Не надо никого тревожить.
Нам надо данное число 
На эту дробь умножить.

 

            Нахождение длины или ширины прямоугольника по его площади можно зарифмовать следующим образом:

 

Если ищем ШИРИНУ,
Делим площадь на длину. 
Хочешь ты найти ДЛИНУ –
Раздели на ширину.

 

            Правила сложения отрицательных чисел и чисел с разными знаками звучат так:

Правила сложения 
Надо детям знать.
Как и умножение –
Выучить, понять.
ЗНАКИ РАЗНЫЕ У ЧИСЕЛ?
Поступаем так:
Модули мы вычитаем,
Большего ставим знак.
ДВА ОТРИЦАТЕЛЬНЫХ?

Мало будет заботы о том:
Минус поставим вначале,
Модули сложим потом 
Если же правила эти
Будете вы выполнять,
Значит вам обеспечено,
Не сомневайтесь, пять!

 

            Правила умножения отрицательных чисел и чисел с разными знаками помогут тоже запомнить рифмованные строчки:

 

Плюс на минус, минус, плюс!
Умноженья не боюсь!
Перемножить модули – это же пустяк.
Самое главное – не забыть про знак.
ПЛЮС НА МИНУС умножая,
Ставим минус не зевая.
ПЛЮС НА ПЛЮС – и плюс в ответе.
Всем пятёрки будут, дети! 
МИНУС С МИНУСОМ умножу,
Плюс в ответе будет тоже.
Выучи стихотворенье –
Веселей пойдёт ученье!

 

            Конечно, математика – наука серьёзная, и учить её надо вдумчиво, но все перечисленные приёмы помогают «учению с увлечением», а значит, и успеху в учении, без которого обучение становится безрезультатным.

 

Глава 2. Практическая часть работы

 

2.1  Стихи в цифрах и без единого слова

 

Цифровые стихи автора работы

 

С. Д. Дрожжин Улицей гуляет Дедушка Мороз. Иней рассыпает По ветвям берез. Ходит, бородою Белою трясет. Топает ногою, Только треск идет.

25   13 306   500 70  15 200  800 37 и 9 225 1012 100 и 35

 

Александр Блок Ветхая избушка Вся в снегу стоит. Бабушка-старушка Из окна глядит. Внукам-шалунишкам По колено снег. Весел ребятишкам Быстрых санок бег... Бегают, смеются, Лепят снежный дом, Звонко раздаются Голоса кругом...	248 325 628 545 74 121 804 901 60 15 232 40 30 20 82…
Сергей Есенин Умей смеяться, когда грустно,  Умей грустить, когда смешно,  Умей казаться равнодушной,  Когда в душе совсем нетто.		149 5 и 8 138 3 и 6 123 и 48 504 26

 

 

Александр Пушкин Под голубыми небесами Великолепными коврами, Блестя на солнце, снег лежит; Прозрачный лес один чернеет, И ель сквозь иней зеленеет, И речка подо льдом блестит.

12 20 39 108 349 108 42 501338 147028 704 3 5 2

 

Цифровые стихи учащихся школы (Приложение В)

 

Агния Барто «Слон» Спать пора! Уснул бычок, Лег в коробку на бочок. Сонный мишка лег в кровать, Только слон не хочет спать. Головой качает слон, Он слонихе шлет поклон.	43  64               49  7  0  8 46  701             309  308 104  48             503  0  25 48  101             45  5  35  60  4  0            607  13  0 3  4  000           9  10  8  0
Расул Гамзатов «Журавли» Мне кажется порою, что солдаты,  С кровавых не пришедшие полей,  Не в землю эту полегли когда-то,  А превратились в белых журавлей.	14  126  17         780  9  30 133  16  37         902  4  27 16  42  517         14  70 и 20 704  97              602  0  57
Владимир Маяковский «Стихи о Советском паспорте» Я достаю из широких штанин Дубликат бесценного груза. Читайте, завидуйте, я — гражданин Советского Союза.	20  08  03 41  800  11 39  600  503 0  400  111

 

 

2.2  Рифмованные правила  и определения по математике

 

Рифмованные правила автора работы

 

Что такое медиана?

Лишь отрезок линии.

От вершины к стороне

Точно посредине.

 

Всем известна биссектриса –

И совсем она не крыса!

Делит угол пополам

И не бегает по углам!

 

Высота – это отрезок,

Что под прямым углом стоит.

Выходит точно из вершины

И свысока на всех глядит.

 

Рифмованные правила учащихся школы (Приложение Г)

 

Сравнение  положительных и отрицательных чисел	Сравнивать я не боюсь  ̶   меньше, чем же + !
Умножение  десятичных дробей	Умножаю дроби десятичные. Умножая, по пути запятую перенеси!
Формула пути	Чтобы рассчитать свой путь, Скорость на время умножать не забудь!
Формула площади прямоугольника	Умножаем a на b назло всякой ерунде. Формулу запоминай, Площадь прямоугольника вычисляй!

 

 

 

Заключение

 

В результате проведенной исследовательской работы, можно сделать следующие выводы:

Связь между математикой и поэзией существует. Математика и поэзия не так далеки друг от друга, как многие думают. Математик подобен художнику, композитору или поэту, он творит и создаёт образы. Его образы - это зашифрованные символами идеи.

Служение науке многие математики 
представляют себе неотрывным от служения поэзии. Поэт должен видеть 
то, чего не видят другие, видеть глубже других. А это должен и математик.

Могущество и красота математической мысли – в предельной чёткости её логики, изяществе её конструкций, искусном построении абстракций. И вместе с тем математические высказывания – определения, теоремы, формулы – сопоставлены с поэзией по силе воздействия на воображение, по целенаправленной плотности языка.

Математические цифры могут «говорить» не только сухим языком математики и помогать в решении примеров и задач, а также выражать радость, грусть в стихах. Цифровые стихи обладают особым обаянием, ярко выраженным ритмом, какой-то необычной энергетикой и, при желании, большой информативностью.

Язык математики - это язык идей, которые со временем изнашиваются меньше, чем слова. Математика всегда гармонична и красива, пожалуй, красота - это самый первый критерий математики. Хотя увидеть математическую красоту трудно, но тоже самое можно сказать и о любой другой красоте, ведь мы не знаем с «абсолютной, объективной» точностью, что подразумеваем под красивой поэмой, но это не мешает нам увидеть ее, когда мы соприкасаемся со стихами, написанными гением. Александр Блок однажды заметил, что самая истинная поэзия, самые настоящие стихи - это «математика слова».

Поэзия математики, как некий сплав искусства и науки. Можно ли быть просто ученым, не будучи творцом? Пожалуй, нет. Для нового нужны идеи, поэтому, не владея идеей невозможно создать нового. И в поэзии красота строки зависит от значимости той идеи, которая заложена в ней. Истинную красоту невозможно приобрести только красивостью слов, равно, как и в музыки, живописи и архитектуре.

Практическая значимость работы:

Ø Активизация и развитие интереса у учащихся к изучению математики в школе.

Ø Использование материала работы на уроках математики, во внеурочной деятельности по математике.

 

Литература

     1.            Агеева И.Д. Занимательные материалы по информатике и математике. – М.: Творческий центр, 2006.

     2.            Allbest – выбери лучшее – Заголовок с экрана - [Электронный ресурс] – Режим доступа   https://allbest.ru/ 

     3.            Большая энциклопедия «Кирилл и Мефодий » – Заголовок  с экрана - [Электронный ресурс] – Режим доступа www.KM.ru

     4.            Волошинов А.В.  «Математика и искусство». «Просвещение» 1992.

     5.            Еженедельная учебно–методическая газета «Математика». Издательский дом «Первое сентября» – Заголовок  с экрана - [Электронный ресурс] – Режим доступа www.1september/ru  

     6.            Журнал «Компьтерра», Москва, 2011, №1 – Заголовок  с экрана - [Электронный ресурс] – Режим доступа https://old.computerra.ru/offline/

     7.            Журнал «Математика для школьников», 2010, №3

     8.            Журнал «Фокус», 2009, №9

     9.            Карпушина Н.М. Любимые книги глазами математика. – М.: Редакция журнала «Наука и жизнь», 2011

 10.            Кодемский Б.А. «Великие жизни в математике». «Просвещение» 1995.

 11.            Методическая газета для учителей математики «Математика», №10, 2011.

 12.            Научно-теоретический и методический журнал «Математика в школе», №8, 2012.

 13.            Панишева О.В. Математика в стихах: задачи, сказки, рифмованные правила. – Волгоград, 2013

 14.            Шейнина О.С., Соловьева Г.М. Математика. Занятия школьного кружка. 5-6 классы. – М.: НЦ ЭНАС, 2001.

 15.            Шустеф Ф.М. Материал для внеклассной работы по математике. – Минск: Народная асвета, 1984.

 16.            Цифровые стихи – Заголовок  с экрана - [Электронный ресурс] – Режим доступа http://mooseum.ru/Iskusstvo/Literatura/Stix/st-02-cifra/cifra-001.html

 17.            Энциклопедия для детей. Математика / Ред. Коллегия: М. Аксёнова, В. Володин –   М.: «Аванта +» , 1998.

   18.          Яндекс.Карточка – Заголовок  с экрана - [Электронный ресурс] – Режим доступа https://yandex.ru/search/?text=Ломоносов%20Михаил%20Васильевич&nomisspell=1&ento=0oCgdydXcxMDI0Eg5ydXczOTc2NTphc3NvYxgCQiHQodC-0YTRjNGPINCa0L7QstCw0LvQtdCy0YHQutCw0Y9FEFY6&source=yobject&clid=2244047&lr=11251&noreask=1

 

 

 

 

Приложение А

 

Математические правила
в стихах	в прозе

 

 

 

 

 

 

 

 

 

 

 

            Приложение Б

 

Рифмованные правила применяются на уроках:

часто

иногда

никогда

предметы

 

 

 

 

 

 

 

Приложение В

Стихи поэтов	Математические стихи
ПРИМЕР  Александр Пушкин из письма Татьяны Евгению Онегину
«Я к вам пишу — чего же боле? Что я могу еще сказать? Теперь, я знаю, в вашей воле Меня презреньем наказать...»		17 20 48 140 10 01 126 138 140 3 501
Агния Барто «Слон» Спать пора! Уснул бычок, Лег в коробку на бочок. Сонный мишка лег в кровать, Только слон не хочет спать. Головой качает сон, Он слонихе шлет поклон.
Расул Гамзатов «Журавли» Мне кажется порою, что солдаты,  С кровавых не пришедшие полей,  Не в землю эту полегли когда-то,  А превратились в белых журавлей.
Сергей Есенин «Береза» Белая береза Под моим окном Принакрылась снегом, Точно серебром. На пушистых ветках Снежною каймой Распустились кисти Белой бахромой. И стоит береза В сонной тишине, И горят снежинки В золотом огне. А заря, лениво Обходя кругом, Обсыпает ветки Новым серебром.
Самуил Маршак «Два кота» Жили-были Два кота - Восемь лапок, Два хвоста. Подрались между собой Серые коты. Поднялись у них трубой Серые хвосты. Бились днем и ночью Прочь летели клочья. И остались от котов Только кончики хвостов.
Владимир Маяковский «Стихи о Советском паспорте» Я достаю из широких штанин Дубликат бесценного груза. Читайте, завидуйте, я — гражданин Советского Союза.
Николай Некрасов «Снежок» Снежок порхает, кружится, На улице бело. И превратились лужицы В холодное стекло. Где летом пели зяблики, Сегодня - посмотри! - Как розовые яблоки, На ветках снегири. Снежок изрезан лыжами, Как мел, скрипуч и сух, И ловит кошка рыжая Веселых белых мух.
ександр Пушкин Мороз и солнце; день чудесный! Еще ты дремлешь, друг прелестный - Пора, красавица, проснись: Открой сомкнуты негой взоры Навстречу северной Авроры, Звездою севера явись!
Роберт Рождественский «Моя бабушка» Со мною бабушка моя, И значит, главный в доме — я, Шкафы мне можно открывать, Цветы кефиром поливать, Играть подушкою в футбол И полотенцем чистить пол. Могу я есть руками торт, Нарочно хлопать дверью! А с мамой это не пройдет. Я уже проверил.
Константин Симонов «Жди меня, и я вернусь» Жди меня, и я вернусь. Только очень жди, Жди, когда наводят грусть Желтые дожди, Жди, когда снега метут, Жди, когда жара, Жди, когда других не ждут, Позабыв вчера.
Федор Тютчев «Умом Россию не понять» Умом Россию не понять, Аршином общим не измерить: У ней особенная стать - В Россию можно только верить.
Омар Хайям Кто понял жизнь тот больше не спешит, Смакует каждый миг и наблюдает, Как спит ребёнок, молится старик, Как дождь идёт и как снежинки тают…
Марины Цветаевой «Родина» О, неподатливый язык! Чего бы попросту — мужик, Пойми, певал и до меня: «Россия, родина моя!»
Корней Чуковский «Телефон»  У меня зазвонил телефон. - Кто говорит? - Слон. - Откуда? - От верблюда. - Что вам надо? - Шоколада. - Для кого? - Для сына моего. - А много ли прислать? - Да пудов этак пять Или шесть: Больше ему не съесть, Он у меня еще маленький!
Григорий Остер «Вредные Советы» Заведи себе тетрадку И записывай подробно, Кто кого на переменке Сколько раз куда послал, С кем учитель физкультуры Пил кефир в спортивном зале, И что папа ночью маме Тихо на ухо шептал.
Эдуард Асадов Берёзка, река, под окном смородина, Друзей — будто звёзд бесконечный свет… Когда тебя знает и помнит Родина, То большего счастья на свете нет!

 

 

 

 

 

 

 

Приложение Г

 

Рифмованные правила

Необходимо сочинить стишок для лучшего запоминания математического правила.

Например:  Умножение и деление чисел с разными знаками:

Умножать я не боюсь,

--  на   --   будет   + !

--    на   +   или   +   на    -- 

какая разница,

будет   --   !

Правила	Рифмованные правила
Сравнение  положительных и отрицательных чисел
Умножение  десятичных дробей
Деление  десятичных дробей
Решение линейных уравнений
Формула пути
Формула периметра
Формула площади
Определение биссектрисы
Определение медианы
Определение биссектрисы
Определение высоты треугольника
Определение прямоугольника
Определение параллелограмма
Определение квадрата
Определение ромба
Определение трапеции
Теорема Пифагора
Другое….

 

 

Скачано с www.znanio.ru

---