Исследовательская работа "Математическая индукция"

Муниципальное образовательное учреждение

«Средняя школы № 93 Советского района г. Волгограда»

«Математическая индукция»

Руководитель: Березенцева И.И.

учитель математики

2021

Оглавление:

Введение………………………………………………………………..2

Глава 1. Теоретическая часть

1.1 История возникновения индукции………………………………..4

1.2 Полная и неполная индукция……………………………………...6

1.3 Метод математической индукции…………………………………8

Глава 2. Практическая часть

2.1 Задачи…..………………...…………………………………..…….9

Заключение......……………………………………………...……….16

Вывод………...…………………………………...…………………..17

Список использованных источников и литературы.........……..18

Введение

Актуальность темы

В математике индукция часто позволяет угадать формулировку теорем, а в ряде случаев и наметить пути доказательств.  Для исследования я выбрал тему «Метод математической индукции», так как в школьной программе с методом математической индукции знакомятся только поверхностно. Знакомство с этим методом полезно учащимся не только из-за расширения их кругозора, но также и потому, что на его принципе основано решение многих задач. Мною был изучен принцип математической индукции, а также его широкое применение в решении задач на суммирование, доказательстве тождеств, доказательстве и решении неравенств (в частности неравенства Бернулли), решении вопроса делимости,  при изучении свойств числовых последовательностей, при решении геометрических задач.

Цель работы

Познакомиться с методом математической индукции, систематизировать теорию по данной теме и применить её при решении математических задач и доказательстве теорем, обосновать и наглядно показать практическое значение метода математической индукции, как необходимого фактора для решения задач.

Задачи работы

1.     Проанализировать литературу по данной теме.

2.     Обобщить и систематизировать знания по данной теме.

3.     Исследовать применение метода математической индукции к решению задач.

4.     Совершенствовать знания, умения, навыки по данной теме.

5.     Развивать творческий подход к решению задач.

6.     Рассмотреть задачи различных видов, применяя в их решении данный метод.

7.     Сформулировать  выводы по данной теме.

8.     Сформировать представления о математики как части общечеловеческой культуры, понимать значимость математики.

1.1 История возникновения индукции

Чтобы познакомится с историей, надо сначала узнать, что же такое математическая индукция. Математическая индукция— один из методов доказательства. Используется, чтобы доказать истинность некоего утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером       n + 1. Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход) . Тогда, если мы толкнём первую косточку (это база индукции) , то все косточки в ряду упадут. Индукция (лат. inductio -- наведение) -- процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не строго через законы логики, а скорее через некоторые фактические, психологические или математические представления. Дедукция (лат. deductio — выведение) - Логическое умозаключение, переход от общих положений к частному, конкретному выводу. Теперь вы знакомы с понятием математическая  индукция.

Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем. Он создал полный список простейших правильных рассуждений, силлогизмов – «кирпичиков» логики, одновременно указав типичные рассуждения, очень похожие на правильные, однако неправильные.

Осознание метода математической индукции как отдельного важного метода восходит к Блезу Паскалю и Герсониду, хотя отдельные случаи применения встречаются ещё в античные времена у Прокла и Эвклида. Современное название метода было введено де Морганом в 1838 году.

Только к концу XIX века сложился стандарт требований к логической строгости, остающейся и до настоящего времени господствующими в практической работе математиков над развитием отдельных математических теорий.

1.2 Полная и неполная индукция

Индуктивное умозаключение – такая форма абстрактного мышления, в которой мысль развивается от знания меньшей степени общности к знанию большей степени общности, а заключение, вытекающее из посылок, носит преимущественно вероятностный характер.

Учитывая зависимость от характера исследования различают полную и неполную индукцию.

Полная индукция - это умозаключение, в ко­тором общее заключение делается на базе изу­чения всех предметов или явлений данного клас­са. В этом случае рассуждение имеет следующую схему:

Полная индукция дает достоверное знание, так как заключение делается только о тех предметах или явлениях, которые перечислены в посылках. Но область применения полной индукции весьма ограничена.

Полную индукцию можно применить, когда появляется возможность иметь дело с замкнутым классом предметов, число элементов в котором яв­ляется конечным и легко обозримым. Она предполагает наличие следующих условий:

а) точное знание числа предметов или явлений, подлежащих изу­чению;

б) убеждение, что признак принадлежит каждому элементу класса;

в) небольшое число элементов изучаемого класса;

г) целесообразность и рациональность.

Вот почему полная индукция чаще всего используется при расследова­нии уголовных дел, связанных с недостачей материальных ценностей. Здесь вывод осуществляется на базе подсчета всех без исключения содержащих­ся на складе или в хранилище предметов путем инвентаризации.

При этом в большинстве случаев юристу приходится иметь дело с такими однородными фактами, количество которых не ограничено или которые не все доступны в настоящее время для непосредственного изучения. Вот поче­му в таких случаях прибегают к использованию неполной индукции, кото­рая на практике применяется значительно шире, чем полная.

Неполная индукция - это умозаключение, в котором на базе повторя­емости признака у некоторых явлений определенного класса делается вывод о принадлежности этого признака всему классу явлений. Неполная индук­ция имеет следующую схему рассуждения:

Неполная индукция часто применяется в реальной жизни, так как позво­ляет делать заключения на базе анализа определенной части данного класса предметов, экономит время и силы человека. Правда, в данном случае мы получим вероятностное заключение, которое исходя из вида не­полной индукции будет колебаться от менее вероятностного к более вероят­ностному.

1.3 Метод математической индукции

Метод математической индукции можно сравнить с прогрессом: мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению логически развивать свою мысль, а значит, сама природа предначертала ему размышлять индуктивно.

Алгоритм:

1.     база - показываем, что доказываемое утверждение верно для некоторых простейших частных случаев n=1;

2.     предположение - предполагаем, что утверждение доказано для первых k случаев;

3.     шаг – доказываем утверждение для случая n=k+1;

4.     вывод - утверждение верно для всех случаев, то есть для всех n.

Заметим, что Методом математической индукции можно решать не все задачи, а только задачи, параметризованные некоторой переменной. Эта переменная называется переменной индукции.

2.1 Задачи

Задача 1. Поставим перед собой такую задачу: составить формулу, выражающую нечетное число u_n через его номер n.

Выпишем в порядке возрастания нечетные положительные числа 1, 3, 5, 7, … Обозначим первое из них  u_1, второе u₂ ,третье u₃ и  т.д., т.е.

u₁ =1,

u₂ =3,

u₃ =5,

u₄ =7,

……..

Решение. Первое нечетное число x₁ можно записать так:

u₁ =2*1-1;                                                  (1)

второе нечетное число u₂ можно записать так:

u₂ = 2*3-1;                                                 (2)

третье нечетное число u₃ можно записать так:

u₃ = 2*3-1.                                                (3)

Внимательно рассматривая равенства (1), (2), (3), можно высказать гипотезу, что для получения любого нечетного числа достаточно от удвоенного номера его отнять 1, т.е. для n-го нечетного числа имеем формулу

                                                             u_{n =} 2n-1.                                                   (4)

Докажем, что формула эта справедлива.

1^°. Равенство (1) показывает, что для n= 1 формула (4) справедлива.

 2^°. Предположим, что формула (4) справедлива для n= k, т.е. k-е нечетное число имеет вид

u_k = 2k-1.

Докажем, что тогда формула (4) обязана быть справедливой и для (k+1)-го нечетного числа, т.е. что (k+1)-е нечетное число имеет вид

u_k+1 = 2(k+1) -1,

или, что все равно,

u_k+1 = 2k+1.

Для получения (k+1)-го нечетного числа достаточно к k-му нечетному числу прибавить 2, т.е.

u_k+1 = u_k+2.

Но, по условию, u_k = 2k-1. Значит,

u_k+1 = (2k-1) +2 =2k+1,

что и требовалось доказать.

Ответ: u_{n =} 2n-1.

Задача 2. Доказать, что сумма квадратов n первых чисел натурального ряда равна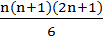 

Решение. Пусть

S₂(n) = 1²+2²+3²+…+n².

1^°. S₂(1) = 1² = .

Значит подставив в правой части за место n, (n+1) получаем

S₂(n+1) = 1²+2²+3²+…+n² + (n+1)² =  ^.,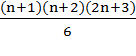

2^°. Предположим, что

S₂(n) = .

Тогда левая часть будет:

S₂(n+1) = 1²+2²+3²+…+n² + (n+1)²  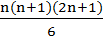=  + (n+1)².

Разложив на множители 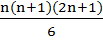 + (n+1)² получаем 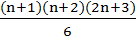 , значит левая часть равна правой. Равенство доказано

Задача 3. Доказать, что любое целое число рублей, больше 7, можно уплатить без сдачи денежными билетами, достоинством в 3 и 5 рублей. Решение. 1^°. Для 8 рублей утверждение справедливо (ибо 8 руб. = 3 руб. + 5 руб.).

2^°. Пусть утверждение верно для k рублей, где k-целое число, больше или равное 8.

Возможны два случая: 1) k рублей уплачивают одними трехрублёвыми билетами и 2) k рублей уплачиваются денежными билетами, среди которых есть хоть один билет пятирублёвого достоинства.

         В первом случае трёхрублёвых билетов должно быть не менее трёх, так как в этом случае k >8. Для того чтобы уплатить k+1 рубль, заменим три трёхрублёвых билета (3+3+3=9) двумя пятирублёвыми (5+5=10). 

         Во втором случае для уплаты k+1 рубля заменим один пятирублёвый (5=5) билет двумя трёхрублёвыми (3+3=6).

Переходы доказаны.

Задача 4.  Доказать, что

2^n-1(aⁿ+bⁿ) > (a+b)²,                                            (1)

где a+b >0, a ≠ b, n-натуральное число, больше 1.

         Решение 1^°. При n=2 неравенство (1) принимает вид

 2(a²+b²) >(a+b)².                                               (2)

Так как a ≠ b, то справедливо неравенство

(a-b)² > 0.                                                         (3)

Прибавив к каждой части неравенства (3) по (a+b)², получим неравенство (2).

Этим доказано, что при n=2 неравенство (1) справедливо.

         2^°. Пусть неравенство (1) справедливо при n=k, где k- некоторое натуральное число, т.е.

2^k-1(a^k+b^k) >(a+b)^k.                                        (4)

Докажем, что тогда неравенство (1) должно быть справедливо и при   n= k+1, т.е.

   2^k(a^k+1+b^k+1 ) >(a+b)^k+1.                                               (5)

         Умножим обе части неравенства (4) на a+b. Так как, по условию,       a+b >0, то получаем следующие справедливое неравенство:

2^k-1(a^k+b^k)(a+b) >(a+b)^k+1.                                          (6)

         Для того чтобы доказать справедливость неравенства (5), достаточно показать, что

2^k(a^k+1+b^k+1) >2^k-1(a^k+b^k)(a+b),                                   (7)

или, что все равно,

a^k+1 + b^k+1 >a^kb + ab^k.                                                  (8)

Неравенство (8) равносильно неравенству

(a^k-b^k)(a-b) >0.                                                            (9)

         Если a >b, то a^k >b^k, и в левой части неравенства (9) имеем произведение двух положительных чисел. Если a < b, то a^k< b^k, и в левой части неравенства (9) имеем произведение двух отрицательных чисел. В обоих случаях неравенство (9) справедливо.

         Этим доказано, что из справедливости неравенства (1) при n=k следует его справедливость при n= k+1.

Задача 5. Доказательство теоремы:

Теорема: Число сочетаний из m элементов по n может быть вычислено по формуле

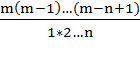= .                                            (1)

         1^°. Прежде всего заметим, что = m и, таким образом, при n=1 формула (1) верна.

         2^°. Допустим, что

= .

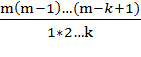Докажем, что

= .

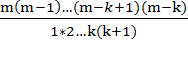         Для получения всех сочетаний из m элементов по k+1 выпишем все сочетания из m элементов по k и к каждому из них в качестве (k+1)-го элемента присоединим каждый из m-k оставшихся элементов.

         Ясно, что таким путём будут получены все сочетания из m элементов по k+1, но каждое из них получится k+1 раз.

         Действительно, сочетание a₁, a₂, …, a_k, a_k+1 получится, когда к сочетанию a₂, a₃, …, a_k, a_k+1 присоединится элемент a₁, когда к сочетанию     a₁, a₃, …, a_k, a_k+1 присоединится элемент a₂ и т.д., когда, наконец, к сочетанию a₁, a₂, …, a_k присоединится элемент a_k+1. Таким образом,

=  =.

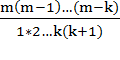Заключение

Итак, индукция (от лат. inductio — наведение, побуждение) — одна из форм умозаключения, приём исследования, применяя который от знания отдельных фактов приходят к общим положениям. Индукция бывает полная и неполная. Метод неполной индукции состоит в переходе к универсальной формулировке после проверки истинности частных формулировок для отдельных, но не всех значений n. Применяя полную индукцию, мы лишь тогда считаем себя вправе объявить об истинности универсальной формулировки, когда убедились в её истинности для каждого без исключения значения n. Метод математической индукции – метод доказательства, основанный на принципе математической индукции. Он позволяет в поисках общего закона испытывать гипотезы, отбрасывать ложные и утверждать истинные.

Метод математической индукции является одной из теоретических основ при решении задач на суммирование, доказательстве тождеств, доказательстве и решении неравенств, решении вопроса делимости, при изучении свойств числовых последовательностей, при решении геометрических задач и т. д.

Знакомясь с методом математической индукции, я изучал специальную литературу, консультировалась с педагогом, анализировал данные и решения задач, пользовался ресурсами Интернета, выполнял необходимые вычисления.

Выводы

В ходе работы я узнал, чтобы решать задачи методом математической индукции нужно знать и понимать основной принцип математической индукции.

Достоинством метода математической индукции является его универсальность, так как с помощью этого метода можно решить многие задачи, а его пошаговость и хорошая алгоритмизированность говорит о простоте применения при доказательстве, что полностью подтверждает нашу гипотезу. Недостатком неполной индукции является то, что порой она приводит к ошибочным выводам.

Обобщив и систематизировав знания по математической индукции, я убедился в необходимости знаний по теме «метод математической индукции». Кроме того эти знания повышают интерес к математике, как к науке. Так же в ходе работы приобрел навыки решения задач по использованию метода математической индукции. Считаю, что эти навыки помогут мне в будущем.

Список использованной литературы

1.     Соминский, И.С. Метод математической индукции [текст]/ И.С. Соминский, Л.И. Головина, И.М. Яглом. Москва 1967

2.     Соловьев, Ю. Математическая индукция [текст]/ Ю.Соловьев, Огюстен Луи Коши, Квант 1991

3.     Виленкин, Н.Я. Индукция. Комбинаторика [текст]/ Н.Я. Виленкин. Москва 1976

4.     Ларин, С.В. Числовые системы [текст]/ С.В. Ларин. Красноярск 2001

5.