
МЕТОД РАЦИОНАЛИЗАЦИИ ПРИ РЕШЕНИИ УРАВНЕНИЙ И НЕРАВЕНСТВ.
Сведения об авторе (авторах):
Верховский Иван Васильевич, МБОУ «СОШ п. Опытный», 11класс
Научный руководитель:
Маряхичева Ольга Александровна, учитель МБОУ «СОШ п. Опытный»
В современном мире каждый человек хочет получить хорошую, престижную профессию, чтобы в дальнейшем обеспечить свою жизнь. Для этого нужно осваивать не только учебный материал, чтобы имея прочные знания получить высокие баллы на ЕГЭ.
Я для себя выбрал инженерно-технический профиль. А это значит, что математика мой профильный предмет. Поэтому мне необходимо, имея прочные знания, набрать как можно большее количество баллов на ЕГЭ, чтобы поступить в престижный ВУЗ на бюджет. Добиться этого довольно непросто: учебного времени не хватает для углубленной подготовки к заданиям высокого уровня сложности, одним из которых является задача 15, приемы и способы решения которой в школьном курсе хоть и рассматриваются, но они слишком объемные и требуют много времени для решения.
Я исследовал решаемость задачи 15(С3) в 2015-2019 годах и вот, что у меня получилось:
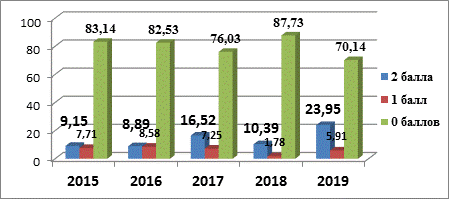 Из диаграммы видно,
что решаемость данной задачи даже в самом лучшем случае не превосходит 24 %.
Конечно задача сложная, но ведь решаемая. Почему же тогда такой низкий %
решаемости?
Из диаграммы видно,
что решаемость данной задачи даже в самом лучшем случае не превосходит 24 %.
Конечно задача сложная, но ведь решаемая. Почему же тогда такой низкий %
решаемости?
Поэтому я решил изучить данную тему, попробовать научиться решать задания 15методом, который был бы легче стандартного . В связи с этим, мною в данной работе рассмотрены способы решения и ряд примеров, большая часть которых взята из вариантов ЕГЭ по математике прошлых лет.
Гипотеза моего исследования заключается в том, что существует метод, позволяющий намного упростить решение задачи 15.
Объект исследования: методы решения уравнений и неравенств.
Предмет исследования: метод рационализации.
Цель данной работы заключается в следующем: научиться решать задания уравнения и неравенства методом рационализации. Для достижения цели я поставил следующие задачи:
1. Изучить математический метод рационализации, используемый при решении задания №15 и выявить плюсы и минусы данного метода.
2.Выбрать типы задач, при решении которых удобнее всего использовать метод рационализации.
3. Создать методическое пособие, содержащее рекомендации по решению задач методом рационализации.
Результатом исследования станут мои высокие баллы по итогам ЕГЭ и приобретение умения решения неравенств методом рационализации, что мне поможет и в дальнейшем обучении в ВУЗе.
Мне стало интересно узнать, существует ли метод решения сложных неравенств (неравенства, содержащие логарифмические, показательные, иррациональные выражения и выражения с модулями) путем замены множителей. Оказалось, что такой метод есть. Называется он – метод рационализации.
При решении неравенств мы используем следующие методы:
1) переход к равносильной системе неравенств или совокупности систем;
2) метод перебора;
3) метод интервалов;
4) метод замены переменной;
5) использование свойств функции: область определения, ограниченность, монотонность.
6) метод рационализации;
Метод рационализации мы используем реже по сравнению с другими методами.
Идея этого метода заключается в том, что неравенства повышенной сложности сводятся к решению рациональных неравенств. Причем достаточно большое количество неравенств можно решить данным методом. Решение неравенства – это объединение конечного числа непересекающихся промежутков. Их легко задать одним рациональным неравенством, что во многих ситуациях позволяет быстрее двигаться к ответу, а иногда получать более эффективные схемы решения типовых неравенств.
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]() h(x)> 0
h(x)> 0
![]()
![]()
Если посмотреть на эти формулы внимательно, то можно заметить, что знак разности g(x) – h(x) совпадает со знаком разности logf(x)g(x) – logf(x)h(x) в случае возрастающей функции (f(x) > 1, т.е. f(x) – 1 > 0) и противоположен знаку разности logf(x)g(x) – logf(x)h(x) в случае убывающей функции (0 < f(x) < 1, т.е. f(x) – 1 < 0). На этом и основан метод рационализации.
Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x), при котором неравенство G(x) ᴠ 0 равносильно неравенству F(x) ᴠ 0 в области определения выражения F(x). (Под знаком ∨ подразумевается один из знаков >, <, ≥, ≤.)
Можно выделить некоторые выражения F и соответствующие им рационализирующие выражения G, где f, g, h, p, k – выражения с переменной x (h>0; h≠1; f>0; g>0), a – фиксированное число (а>0; a≠1).
|
Выражение F |
Выражение G |
|
log ₐ f – logₐ g log ₐ f - 1 log ₐ f |
(a - 1)(f – g) (a - 1)(f – a) (a - 1)(f – 1) |
|
log h f – loghg log h f – 1 log h f |
(h −1)( f − g) (h −1)( f − h) (h − 1)( f − 1) |
|
Log f h – logg h (g≠1, f≠1) |
( f −1)(g −1) ×(h − 1)(g − f ) |
|
hᶠ - hᶢ (h>0) hᶠ - 1 |
(h −1)( f − g) (h −1) f |
|
f ⁿ- gⁿ ( f > 0; g > 0) |
( f − g)h |
|
|f| - |g| |
( f − g)( f + g) |
Тогда имеют место следующие выражения:
logh f · log p q ↔ (h - 1)(f - 1)(p - 1)(q - 1)
logh f + log h g ↔ (fg - 1)(h - 1)
√f - √g ↔ (f - g)
(hᶠ - hᶢ) /(hᵖ - hᵏ) ↔ (f - g)/(p - k) .
Алгоритм метода рационализации
1. Рассмотреть ОДЗ неравенства.
2. Заменить исходное неравенство неравенством из второй колонки таблицы.
3. Упростить полученное неравенство
4. Решить полученное рациональное неравенство.
5. Записать ответ исходного неравенства, учитывая ОДЗ.
Решить
неравенство: ![]()
|
(метод рационализации)
Решение:
Ответ:
|
( традиционный метод)
Решение: 1)
ОДЗ:
a)
б)
Ответ:
|
Решение неравенств, содержащих модули, методом интервалов с применением метода рационализации.
Пример №1. Решить неравенство
![]()
По формуле |f(x)| - |g(x)| ó (f(x))2 – (g(x))2
![]()
![]()
![]()
![]()
Решаем неравенство методом интервалов, получаем
Ответ: (-∞; -2), [ -1; 1], (2; 4).
Решение иррациональных неравенств.
Решить неравенство
![]()
2x2+x+1≥0
x2+x+1≥0
![]()
![]()
![]()
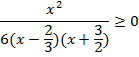
Решаем методом интервалов и получаем:
Ответ: (-∞; -3/2), {0}, (2/3; +∞).
Решение логарифмических неравенств.
Решить неравенство:
![]() Решение этого неравенства см. выше.
Решение этого неравенства см. выше.
Решение показательных неравенств.
Решить неравенство:
![]()
Я просмотрел задачи задания 15(С3) за 2015-19 годы. В реальных экзаменационных вариантах я нашел следующие задачи:
2015-2016 г
Решите неравенство ![]()
![]()
![]()
2016-2017 г.
Решите неравенство 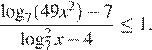
Решите неравенство: ![]()
Данные неравенства легче всего решаются методом замены переменной, а решить их методом интервалов достаточно сложно.
2017-2018 г.
Решите
неравенство ![]()
2018-2019 г.
Решите неравенство 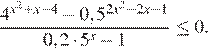
Решение этих задач методом рационализации см в Приложении 1.
Конечно, сразу видно, что решение неравенства методом рационализации гораздо короче и проще. Но среди неравенств, которые я разбирал в реальных вариантах ЕГЭ предыдущих лет, есть и такие, которые сложно решить методом рационализации или проще решить другим методом.
Например
неравенство ![]() удобнее решить
методом замены переменной.
удобнее решить
методом замены переменной.
Это говорит о том, что Метод рационализации – не панацея, а всего лишь один из методов решения. И пользоваться им или нет, каждый решает сам.
Умение решать показательные, иррациональные и логарифмические неравенства очень важно для успешной сдачи ЕГЭ по математике.
Итак, работая над темой, я пришел к следующим выводам:
1. В процессе исследования темы я нашел такой способ решения неравенств, как метод рационализации, с помощью которого можно заменить сложные неравенства, более простыми - рациональными неравенствами. Метод рационализации позволяет существенно упростить решение сложных неравенств в задании 15 ЕГЭ профильного уровня по математике, но не для каждого неравенства он является наиболее удобным способом решения.
2. Методом рационализации удобнее всего решать логарифмические, показательные, иррациональные неравенства и неравенства с модулем.
3. Я создал методическое пособие для решения неравенств методом рационализации, которое, я надеюсь, позволит мне и моим одноклассником успешно решить задание 15.
Используемая литература:
1. https://shkolkovo.net/catalog/reshenie_neravenstv/_metodom_racionalizacii
2. https://egemaximum.ru/metod-racionalizacii-chast-1/
3. https://yourtutor.info/
4. https://ege.sdamgia.ru
Метод рационализации при решении неравенств.
Пособие для учеников 10-11 классов.
Составители : ученик 11 а класса МБОУ «СОШ п. Опытный»
Цивильского района Чувашской республики
Верховский Иван Васильевич
Учитель математики «СОШ п. Опытный»
Цивильского района Чувашской республики
Маряхичева Ольга Александровна
Содержание
1. Пояснительная записка 1
2. Метод рационализации при решении неравенств, содержащих логарифмические функции. 2
3. Метод рационализации при решении неравенств, содержащих иррациональные выражения. 10
4. Метод рационализации при решении неравенств, содержащих модули. 13
5. Метод рационализации при решении неравенств, содержащих показательные функции. 16
6. Заключение. 18
7.Список литературы. 18
Пояснительная записка.
Самым легким способом решения неравенств является способ решения рациональных неравенств методом интервалов, но не все неравенства имеют структуру, которая позволяет решать их этим методом. Поэтому цель работы – предложить метод решения сложных неравенств (неравенства, содержащие логарифмические, показательные, иррациональные выражения и выражения с модулями) путем замены множителей. Идея этого метода заключается в том, что неравенства повышенной сложности сводятся к решению рациональных неравенств. Оказывается, достаточно широкий класс неравенств подобную попытку допускает. Решение неравенства – это объединение конечного числа непересекающихся промежутков. Их легко задать одним рациональным неравенством, что во многих ситуациях позволяет быстрее двигаться к ответу, а иногда получать более эффективные схемы решения типовых неравенств.
Метод рационализации при решении неравенств, содержащих логарифмические функции.
Разность логарифмов по одному и тому же основанию всегда по знаку совпадает с произведением разности чисел этих логарифмов на отклонение от единицы. Другими словами выражение вида (logaf – logag) имеет тот же знак (в области существования логарифмов) что и выражение (f-g)(α-1)
Выделим некоторые выражения и соответствующие рационализирующие выражения, позволяющие исключительно эффективно решать многие логарифмические неравенства, которые можно отнести к разряду повышенной сложности.
|
Выражение F |
Выражение G |
|
log ₐ f – logₐ g log ₐ f - 1 log ₐ f |
(a - 1)(f – g) (a - 1)(f – a) (a - 1)(f – 1) |
|
log h f – loghg log h f – 1 log h f |
(h −1)( f − g) (h −1)( f − h) (h − 1)( f − 1) |
|
Log f h – logg h (g≠1, f≠1) |
( f −1)(g −1) ×(h − 1)(g − f ) |
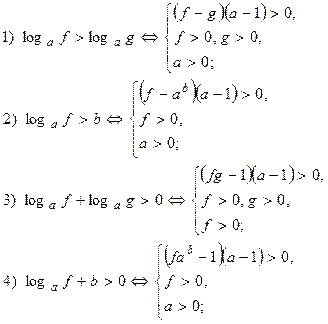 Или
так
Или
так
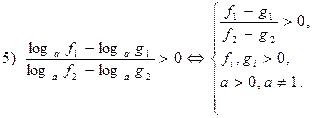
Примеры решения
логарифмических неравенств методом рационализации.
Приведем сравнение решения неравенства традиционным методом и методом рационализации:
№1. Решить неравенство:
![]()
|
(метод рационализации) ( традиционный метод) |
||
|
№2. Решить
неравенство:![]()
Решение:
![]()
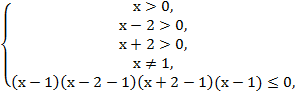
![]()
2![]()
![]() 2
2![]()
№3.Решить неравенство:![]()
Решение:
![]() ,
, ![]()
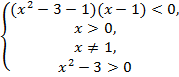
![]()
![]()
![]()
Ответ: (![]()
№4. Решить
неравенство ![]()
Решение:
![]() ,
,![]() ,
,
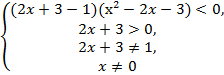
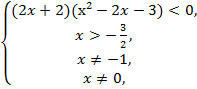
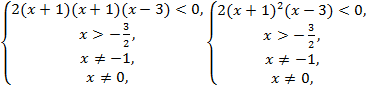
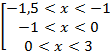
Ответ:
(-1,5;-1)![]() (-1;0)
(-1;0)![]() (0;3)
(0;3)
№5. Решить
неравенство ![]()
Решение:![]()
![]() ,
,
![]() ,
,
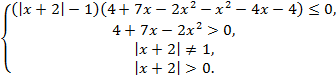
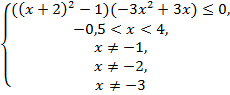
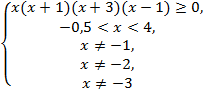
Ответ: (-0,5;![]()
№6. Решить
неравенство
![]() Решение:
Решение:
![]()
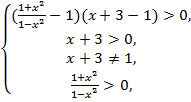
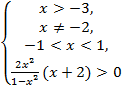
![]()
![]()
Ответ:
(-1;0)![]()
№7. Решить
неравенство :![]() .
.
Решение:
![]() ,
,![]() ,
,
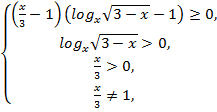
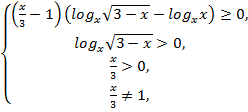
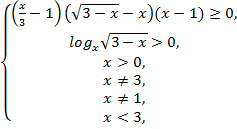
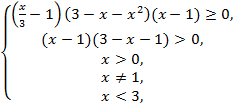
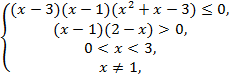
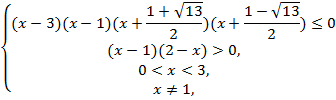
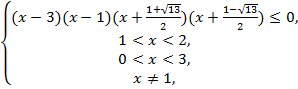
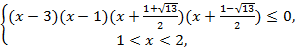
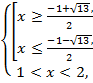
![]()
Ответ:
![]()
№8. Решить
неравенство ![]()
Решение:
![]() ,
,
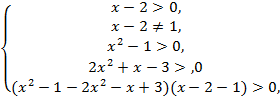
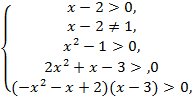
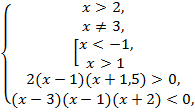
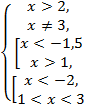
![]()
![]()
Ответ: ![]()
№9. Решить неравенство ![]()
Решение:
![]()
а)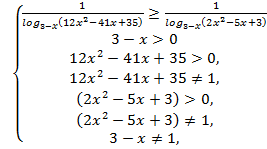
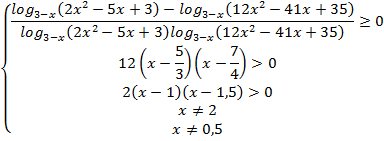
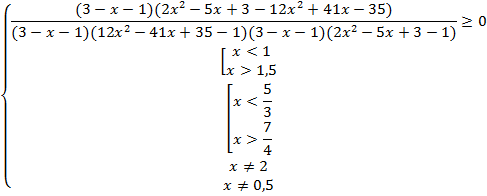
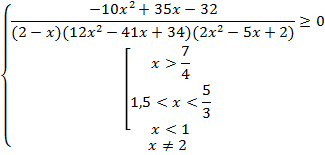
![]()
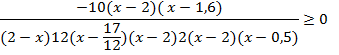
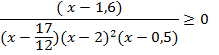
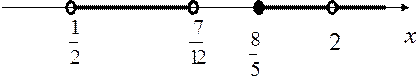
0,5![]() , 1,6
, 1,6![]()
Имеем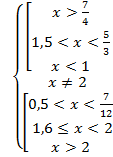
следовательно ![]() ;
;![]() ;
;![]()
б) если x-3=1,
x=2- не является решением (при x=2
![]() ) .
) .
Ответ:![]() ;
;![]() ;
;![]()
№10. Решить
неравенство![]()
Решение:
![]()
![]() ,
,
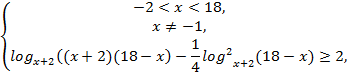
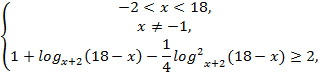
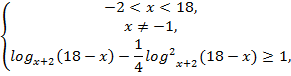
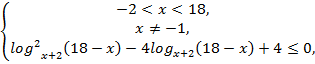
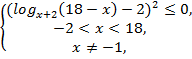
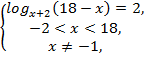
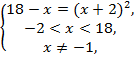
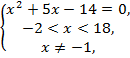
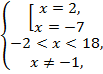
![]()
Ответ: ![]()
№11. Решить
неравенство ![]()
Решение:
![]()
![]()
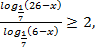
![]()
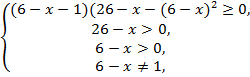
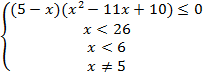
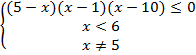 1
1![]()

Ответ: 1![]()
№12. Решить
неравенство ![]()
Решение:
![]()
![]()
![]() )
)![]()
![]()
![]()
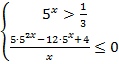
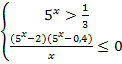
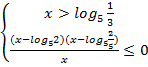
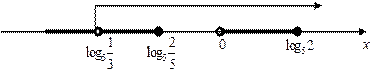
![]() ; 0
; 0![]()
Ответ:![]() ; 0
; 0![]()
№13. (Применение метода рационализации при решении неравенств с параметрами)
Решить неравенство.
![]()
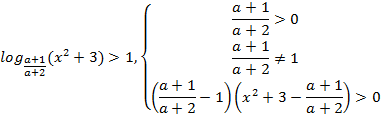
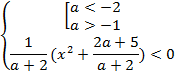
Рассмотрим два случая.
1)Пусть ![]() . Тогда получим, что
. Тогда получим, что ![]() и
и ![]() следовательно,
следовательно,
![]() для
любых x, что не удовлетворяет
условию задачи.
для
любых x, что не удовлетворяет
условию задачи.
2) Пусть теперь ![]() . В этом случае
. В этом случае ![]() и, для того чтобы
неравенство
и, для того чтобы
неравенство ![]() было верно для любых x
, необходимо и достаточно, чтобы выполнялось условие
было верно для любых x
, необходимо и достаточно, чтобы выполнялось условие ![]() .
.
Получим систему:
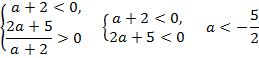
Ответ: (![]() )
)
Метод рационализации при решении неравенств, содержащих иррациональные выражения.
При решении неравенств, содержащих иррациональные
выражения, используем следующее правило ![]() -
-![]() (на области определения)
(на области определения)
№1.Решите неравенство:
![]()
Решение.
![]()
![]()
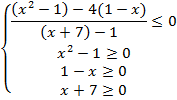
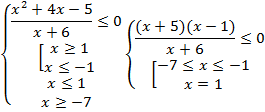
-7![]()
Ответ:
-7![]() 1
1
№2.Решите неравенство
![]()
Решение:
![]()
![]()
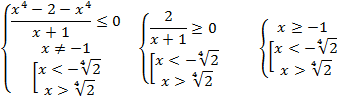
![]()
Ответ:
![]()
№3Решите неравенство
![]()
Решение:
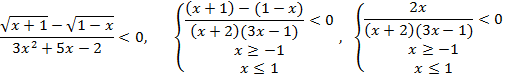
![]()
Ответ:
0![]()
№4Решить неравенство:
![]()
Решение:
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
№5 Решить неравенство:
![]()
Решение:
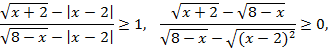
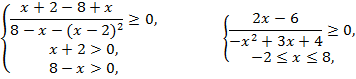
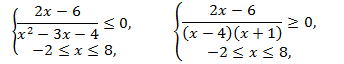
![]()
![]()
Ответ:
![]()
№6.Решить
неравенство:
![]()
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Метод рационализации при решении неравенств , содержащих модули.
Опорная информация, позволяющая указать удобные замены, заключается в двух основных свойствах модуля:
│m│2 = m2 и │m│≥0 для всех m,
а также в монотонном возрастании на множестве неотрицательных чисел функции y=t2.
Приведем типы замен:
![]() ,
,
![]() ,
,
![]()
![]()
![]()
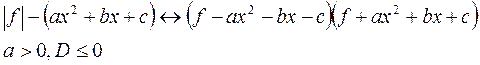
№1.![]()
![]() :
: ![]()
![]()
(![]() ,
,
(10x+32)(2![]() (10x+32)2x(x+5)
(10x+32)2x(x+5)![]() ,
,
-5![]()
![]()
Ответ:
-5![]()
Для
решения дробных неравенств, содержащих модули удобно использовать следующее
правило:
![]()
![]()
![]()
Решение:
![]()
![]()
-6![]()
Ответ:
-6![]()
№3.Решить
неравенство:
![]()
Решение:
![]()
![]()
![]()
![]()
-9![]()
Ответ:
-9![]()
№4.Решить
неравенство:
![]()
Решение:
![]()
![]()
![]()
![]()
x![]() , 2
, 2![]() 4
4![]()
Ответ:
x![]() , 2
, 2![]() 4
4![]()
№5.Решить
неравенство:
![]()
Решение:
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
x![]()
№6. Решить неравенство:
Решение:
![]()
![]()
![]()
![]()
![]() x
x![]() , 3
, 3![]()
Ответ:
x![]() , 3
, 3![]()
№7. Решить
неравенство:
![]()
![]()
![]()
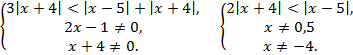
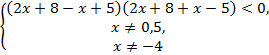
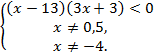
-13![]()
Ответ:
-13![]()
![]() Решить неравенство:
Решить неравенство:
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Метод рационализации при решении неравенств, содержащих показательные функции
Можно установить, что разность степеней по
одному и тому же основанию всегда по знаку совпадает с произведением разности
показателей этих степеней на отклонение основания степени от единицы. Другими
словами, выражение вида ![]() имеет
тот же знак, что и выражение
имеет
тот же знак, что и выражение
(f –g)(а – 1) при а> 0
(если а=1, то выражения равны нулю)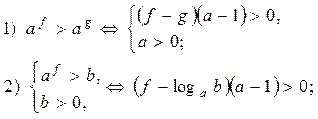
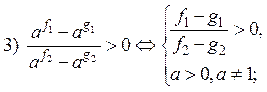
№1.Решить неравенство:
![]()
Решение:
![]() ;
;
![]()
Ответ:
![]()
№2.Решить неравенство:
![]()
Решение:
![]()
![]()
Ответ: ![]()
№3.Решить неравенство:
![]()
Решение:
![]()
![]()
![]()
Ответ: ![]()
№4.Решить неравенство:
![]()
Решение:
![]() ;
;
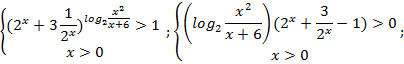
![]()
![]()
Ответ:
![]()
№5.Решить
неравенство:![]()
Решение:![]() . На множестве
. На множестве ![]()
исходное
неравенство равносильно ![]()
x(2x+1)(3x-7)![]()
Получим
![]()
Ответ:
![]()
№6.Решить неравенство
![]()
Решение:
Область определения неравенства: ![]()
![]()
Применим метод рационализации неравенства:
![]()
![]()
(x+1)x(x-1)![]()
![]()
Ответ:
![]()
№7.Решить неравенство
![]()
Решение:
Первый множитель в числителе заменяем на ![]() , второй на
, второй на ![]() , третий на
, третий на![]() , четвертый на
, четвертый на
![]() , пятый на
, пятый на ![]() .
.
Первый множитель в знаменателе заменяем на![]() , а второй на
, а второй на ![]() .
.
Получаем в области допустимых значений рациональное неравенство, равносильное исходному:
![]()
Область существования
всех множителей в исходном неравенстве представляет собой два промежутка: ![]() . В этой области множители
. В этой области множители ![]() знакопостоянны, и поэтому их знаменяем
соотвестственно на (-1) и 1.
знакопостоянны, и поэтому их знаменяем
соотвестственно на (-1) и 1.
Знакопостоянны
и трехчлены ![]() , поэтому их заменяем также, соответственно
на (-1) и 1.
, поэтому их заменяем также, соответственно
на (-1) и 1.
![]()
Решая последнее стандартное рациональное неравенство в указанной области существования всех множителей исходного неравенства, получаем ответ:
![]() .
.
Заключение.
При составлении пособия мы проанализировали сборники по подготовке к ЕГЭ по
математике. Многие задания части ![]() содержат неравенства, содержащие
неизвестное в основании логарифма, решение которых требует громоздких
выкладок и больших затрат времени. Метод рационализации. позволяет сократить
время при решении такого типа неравенств. Этот способ распространяется и на
решение других неравенств - показательных, иррациональных и неравенств,
содержащих модули). Самым основным можно считать следующее:
содержат неравенства, содержащие
неизвестное в основании логарифма, решение которых требует громоздких
выкладок и больших затрат времени. Метод рационализации. позволяет сократить
время при решении такого типа неравенств. Этот способ распространяется и на
решение других неравенств - показательных, иррациональных и неравенств,
содержащих модули). Самым основным можно считать следующее:
1) Основная идея метода рационализации состоит в замене любого множителя А на знакосовпадающий с ним и имеющий одни и те же корни(в области определения) множитель B.
2) Преобразованные таким образом неравенства всегда равносильно исходному в области определения последнего.
3) Указанная замена возможна только тогда, когда заменяемый множитель находится в числители или знаменателе дроби, которая сравнивается с нулем.
4) По внешнему виду неравенства легко определяется возможность применения метода рационализации.
Эта работа может быть использована при подготовке к ЕГЭ. Здесь собрано достаточное количество формул и решенных неравенств, которые помогут любому выпускнику изучить этот метод.
Список литературы.
1) В помощь абитуриентам/Составители В. И. Голубев, А. А. Егоров, В. А. Тихомирова.- М.: Бюро Квантум,2009( приложение к журналу КВАНТ)
2)Егэ-2013. Математика: типовые экзаменационные варианты:30 вариантов / под ред. А. Л. Семенова, И. В. Ященко. –М.: Издательство «Национальное образование»,2012.-192с.-(ЕГЭ-2013. ФИПИ – школе.)
3) Задачи вступительных экзаменов/ Составители А. А. Егоров, В. А. Тихомирова.- М.: Бюро Квантум,2008(приложение к журналу КВАНТ)
4) «Квант» 2006/№4, В.Голубев, «Метод замены множителей»
5)Математика. ЕГЭ: сборник заданий: методическое пособие для подготовки к экзамену / Ю. А. Глазков, Т. А. Корешкова, В. В. Мирошин, Н. В. Шевелева. – 3-е изд., испр.- М.: Издательство «Экзамен»,2010.-287с. ( Серия « ЕГЭ. Сборник заданий. »
6) Подготовка к ЕГЭ по математике в 2012 году. Методические указания/Ященко И. В., Шестаков. С. А., Трепалин А. Сю, Захаров П.И.-М.: МЦНМО,2012.
7)Самое полное издание типовых вариантов реальных заданий ЕГЭ:2010: Математика/ авт.-сост. И. Р. Высоцкий, Д. Д. Гущин, П. И. Захаров и др.; под ред. А. Л. Семенова, И.В. Ященко. – М,:АСТ: Астрель,2010.- 93с.-( Федеральный институт педагогических измерений.)
8)«Сборник задач по математике для поступающих в Вузы». Уч. Пособие / под ред. М. И. Сканави.- М.: Высшая шк.,1988.
9)«Эффективные пути Решения неравенств». Уч. Пособие / под ред. В. И. Голубева , В. А. Тарасова.1992.
10) www.alexlarin.narod.ru – Корянов А. Г., Прокофьев А. П. Метод решения неравенств с одной переменной.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.