Исследовательская работа "Практическое применение теоремы Пифагора"

Государственное учреждение образования

«Гимназия № 38 г. Минска»

 

 

Исследовательская работа

по математике

 

«Практическое применение теоремы Пифагора»

Выполнили: Матвеева Алёна, 8 «Г» класс,

                                                                                   Бруева Элеонора, 8 «Г» класс

Руководитель: Милевская Т.Е.

 

 

2021 год

       

 

  Пояснительная записка

«Геометрия владеет двумя сокровищами:

одно из них –  это теорема Пифагора»  Иоганн Кеплер

 

Актуальность: по выражению известного ученого Иоганна Кеплера, «геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».

Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что с ее помощью можно вывести большинство теорем геометрии.

Один американский математик, наш современник, около 20 лет собирал различные способы доказательства теоремы Пифагора, и сейчас его «коллекция» содержит около 300 различных доказательств. Это говорит о том, что древняя теорема актуальна и интересна людям до сих пор.

Новизна: в школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. К сожалению, вопрос о практическом применении теоремы Пифагора не рассматривается.

         В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

Объект исследования:  теорема Пифагора.

Предмет исследования: различные интерпретации и  способы доказательства теоремы Пифагора, ее применение  при решении практических задач.

Изучая дополнительную литературу по выбранной теме, были  выдвинуты гипотезы:

    1)существуют другие интерпретации теоремы Пифагора;

    2)теорема Пифагора применяется при решении многих практических задач.

    3) За красоту и гармонию в природе «отвечает» математика. То есть, особые числовые

       закономерности существуют во всем, что нас окружает.

    4) С помощью теоремы Пифагора можно решать не только математические задачи.

Цели исследования:

- внимательно изучив формулировку  теоремы Пифагора, проанализировав доказательства и используя обобщение, рассмотреть иные интерпретации теоремы Пифагора;

- выяснить области применения теоремы Пифагора

Для достижения цели были поставлены следующие задачи:

1.      Провести анализ истории возникновения теоремы Пифагора и творческой деятельности Пифагора.

2.      Исследовать различные способы доказательства и рассмотреть иные интерпретации теоремы Пифагора.

3.      Показать практическое применение теоремы Пифагора.

Практическая  значимость:

•        Использование  приобретенных знаний и навыков исследовательской работы  при изучении других школьных предметов.

•        Расширение и углубление знаний учащихся по данной теме.

•        Формирование навыков исследовательской деятельности учащихся.

•        Развитие познавательной активности учащихся, повышение интереса к предмету.

•        Совершенствование навыков работы с математической литературой.

Умения и навыки:

•        Организация  и проведение   эксперимента.

•        Использование  специальной литературы.

•        Приобретение  умения  делать обзор  собранного материала (доклад, презентацию, реферат).

•        Оформление работы    рисунками, диаграммами, фотографиями.

•        Активное  участие   в обсуждении  своей работы.                                            

       

 

Оглавление

 

 

     I  Введение. ……………………………………………………………………стр.4 – 5

 

    II Основная часть………………………………………… стр. 6 – 23

 

1. Немного о Пифагоре………………………………………………………стр.6 - 8

2. История возникновения теоремы Пифагора………………………………стр.8 - 9

3. Различные способы доказательства теоремы Пифагора.. …………стр.10-15

4. Исторические задачи………………………………………………………стр.15-16

5. Теорема Пифагора в

·        строительстве и архитектуре……………………………………………стр.17-19

·        мобильной связи…………………………………………………………стр.20

·        литературе………………………………………………….тр.20-21

 

III. Заключение …………………………………………………………………стр.22

 

      IV. Литература…………………………………………………………………стр.23

 

 

 

      

 

 

 

 

 

 

 В школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. Вопрос о практическом применении теоремы Пифагора почти не рассматривается. В связи с этим, целью нашей  работы было выяснить области применения теоремы Пифагора.

         В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство.

Гипотеза:

1)  Существуют другие интерпретации теоремы Пифагора;

2) С помощью теоремы Пифагора можно решать многие практические задачи.

Цель: выяснить области применения теоремы Пифагора.

Задачи:

1.     Собрать информацию о практическом применении теоремы Пифагора в различных источниках и определить области применения теоремы.

2.     Изучить некоторые исторические сведения о Пифагоре и о его теореме.

3.     Показать применение теоремы при решении исторических задач.

4.     Обработать собранные данные по теме.

5.     Оформить наработанный материал в виде проекта.

 

 

 

 

 

 

 

 

 

 

Пифагор  и его теорема

       В Интернете мы самостоятельно ознакомились с практическим применением теоремы и историческими задачами. Вопрос о практическом применении теоремы Пифагора и о самом Пифагоре в школьном учебнике геометрии В.В.Казакова, по которому занимались мы,  не освещен. Упоминается лишь немного о биографии Пифагора и о том, как древние египтяне строили прямые углы с помощью веревки, разделенной на 12 равных частей (3,4,5).

    

      Великий ученый Пифагор родился около 570 г. до н.э. на острове Самос (откуда и пошло прозвище Пифагор Самосский), одном из самых цветущих островов Ионии, у берега Малой Азии,  в семье богатого ювелира. Он был очень красив и с детства отличался разумом и справедливостью. С юных лет Пифагор стремился проникнуть в тайны Вечной Природы, постичь смысл Бытия.        

       Пифагор – это греческий ученый, религиозный и политический деятель. Трудно сказать, какие научные идеи принадлежали Пифагору, какие – его воспитанникам. Но рассказывают, что Пифагор, доказав свою знаменитую теорему, отблагодарил богов, принеся им в жертву 100 быков. 

   

 

 

 

 

 

 

 

 Другие формулировки теоремы.

     У Евклида эта теорема гласит (дословный перевод):

   "В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".

   В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так :

"Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".

   Во времена Пифагора формулировка теоремы звучала так: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах» 

Современная формулировка теоремы гласит:

«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Различные способы доказательства теоремы Пифагора

   Существует более 500  доказательств теоремы Пифагора. Она даже занесена в книгу рекордов Гиннеса!  Простейшее доказательство теоремы есть у древнегреческого математика Евклида. Ученые считают, что это доказательство теоремы Евклид придумал сам. В древности, теорему Пифагора знали лишь отдельные ученые, посвященные в таинства математики, теперь ее учат все.

Пифагором сначала был доказан лишь частный случай теоремы: им рассматривался равнобедренный прямоугольный треугольник. Чертеж, который используют для доказательства этого случая, в шутку называют «пифагоровы штаны» и добавляют: во все стороны равны.

Знакомясь с разными способами доказательства теоремы Пифагора, мы заметили, что одни из них основаны на свойстве равносоставленных фигур,  другие – на дополнении до равных фигур, а третьи - на свойстве равновеликих фигур (имеющие равные площади).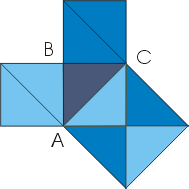

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Например, для такого треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по 2. Теорема доказана. 

 

 

 

 

 

 

 

 

 

 

 

 

Теорема Пифагора в исторических задачах

Предлагаем несколько исторических  задач, найденных в древних источниках.

 Задача Бхаскари

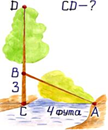
 «На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
 У тополя как велика высота?»

Решение: По теореме Пифагора АВ²= ВС²+АС² ;9+16=25, АВ=5 Футов; СD=3+5=8 футов. Ответ: высота тополя 8 футов.

Задача из китайской «Математики в девяти книгах»

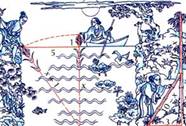«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды, и какова длина камыша?».   Решение: По теореме Пифагора (x+1)²=x²+25; 2x=24, x=12 чи.; 12+1=13 чи.

Ответ: глубина воды-12 чи, длина камыша-13 чи.

Задача из учебника «Арифметика» Леонтия Магницкого 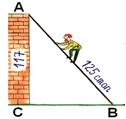                                      «Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать». Решение: ВС²=АВ²-АС²; ВС²=15625-13689=44 стоп. Ответ: ВС=44 стоп. (Приложение№3). 

Теорема Пифагора в  строительстве и архитектуре

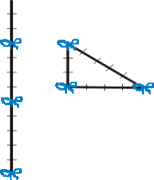             Очень легко можно воспроизвести способ построения

"натягивателями веревок" прямых углов при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным

между сторонами длиной в 3 и 4 метра. 

Мы попробовали сами применить этот метод для получения прямого угла на местности.

 

Строительство крыши

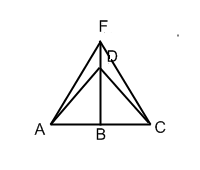     При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.      Решение:     Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда из треугольника DBC: DB=2,5 м.,  из треугольника АВF:  АF=√4²+4²=√32≈5,7 м. 

     

Мы знаем теперь, что для строительства крыши дома обязательно надо применить теорему Пифагора. При проектировании любых строительных объектов возникает необходимость вычислять стороны прямоугольных треугольников по известным сторонам. Подобные задачи решаются и в нашей повседневной жизни.

 

Теорема Пифагора в реальной жизни

Когда мы проводили на дачу свет, нам надо было рассчитать длину  электрического провода от домика высотой 2,5м  до столба высотой 8,5м.

«Выручила»  теорема Пифагора . (Расстояние от  столба до домика 8 м)

 

 

 

Установка  ёлки

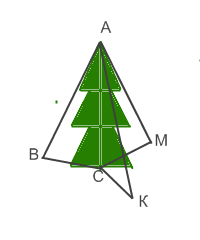На Новый год всюду устанавливают елки. Ёлка стоит неустойчиво (это проблема) и под воздействием природных явлений (чаще сильного ветра) накреняется и может  упасть. Нужно установить ёлку высотой 8м. и закрепить её в вертикальном положении. Для этого от вершины ёлки надо сделать проволочные натяжки АВ, АМ, АК одинаковой длины и закрепить на земле на расстоянии 6м от основания елки.

 

Длина натягивающей проволоки должна 10м., т.к. по теореме Пифагора АВ²= АС²+ВС²;

АВ==10 м.

 

В мобильной связи

         В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе.

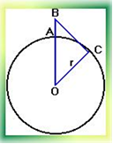
Задача: Какую наименьшую высоту должна иметь вышка мобильной связи, поставленной в аг Колодищи, чтобы микрорайон Уручье попал в зону связи (расстояние от вышки до Уручья по прямой 10 км.)?  Радиус Земли около 6380 км.

Решение: Применив теорему Пифагора, получили уравнение

(х+6380)²=10²+6380²;

х²+12760х-100=0;

D=162817600+400=162818000;

≈12760,016;

х≈0,008км.

 

В  литературе

      Мало кто знает, что Пифагор имел отношение не только к математике, но и к литературе. Он и его теорема воспеты в литературе. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист  Плутарх, греческий ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.

Так, например, немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в кругосветном путешествии на корабле "Рюрик", написал следующие стихи:

Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье.

За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать.

От страха, что вселил в них Пифагор.

        Теоремой Пифагора и пифагорейской школой восхищается человечество на протяжении всей истории, им посвящают стихи, песни, рисунки, картины.

Так художник Ф.А. Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу»

Картина передает пафос преклонения учеников легендарной школы перед единой гармонией, царящей в мироздании («космосе»), музыке и числе.

Практико-ориентированные задачи:

    Мы попробовали составить свои задачи, которые можно предложить на уроке при изучении теоремы Пифагора, чтобы подчеркнуть её практическую значимость.

Задача 1 Пожарная лестница длиной 12,5 м приставлена к стене так, что расстояние нижнего конца лестницы от стены равно 3,5 м. Хватит ли этой лестницы, чтобы пожарники могли попасть в окно, находящееся на высоте 11,5 м от земли? 

Задача 2 Вертикальная мачта поддерживается четырьмя канатами. Прикрепленными к ней на расстоянии 16 м от земли и к земле на расстоянии 12 м от основания мачты. Сколько метров каната потребовалось монтажникам для укрепления мачты, если на узлы пошло 5 м? 

 Задача 3 Для монтажа крыши, строителям надо установить стропила на балке. Какой длины надо взять стропила, чтобы длина балки составляла 8м, а стропила образовывали прямой угол?

Задача 4  От столба высотой 9 м к дому электрики натянули провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину данного провода.

Задача 5*   ПРОЕКТ   

  1. Определите примерную длину лестницы, которая идёт к окну второго этажа дома, если расстояние от этого этажа до земли 6 м, а расстояние от фундамента дома до основания лестницы равно 3 м.

2. Подсчитайте, сколько метров бруска пойдёт на изготовление такой лестницы, если у неё 18 ступенек и ширина лестницы равна 50 см.

3. Рассчитайте стоимость изготовления такой лестницы, если цена 1 метра бруска составляет 6 рублей 40 коп.

     

 

 

 

 

 

 

 

Заключение

       В результате проведённого исследования мы выяснили некоторые области применения теоремы Пифагора. Нами собрано и обработано много материала из литературных источников и интернета по данной теме. Мы изучили некоторые исторические сведения о Пифагоре и его теореме, решили ряд исторических задач на применение теоремы Пифагора.

Значение теоремы Пифагора состоит в том, что с ее помощью можно вывести большинство теорем геометрии и решить множество задач.  Благодаря такому количеству доказательств, теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и  идей.

Результатом нашей работы является:  

1.      приобретение навыка работы с литературными источниками;

2.      приобретение навыка поиска нужного материала в Интернете;

3.      научились работать с большим объёмом информации, отбирать нужную информацию;

4.     собранный нами материал может быть полезен при изучении теоремы Пифагора в курсе геометрии;

5.   мы подтвердили гипотезу, что теорема Пифагора имеет широкое практическое применение.

     Было интересно почувствовать себя исследователем, но главное нас заинтересовал процесс познания. Работа над проектом помогла нам реально применить полученные на уроках знания, навыки, опыт в практической деятельности, в соответствии с нашими интересами.

 

Скачано с www.znanio.ru