Исследовательская работа "Божественная пропорция, или как измерить гармонию".

Аннотация

На протяжении тысячелетий человек старается находить различные методы достижения идеальной красоты.   Один из таких способов - золотое сечение. Области, в которых мы можем встретить использование золотой пропорции, многообразны.   

 Целью  работы является исследование    различных областей жизнедеятельности человека,   в которых встречается гармоническая  пропорция. Для достижения этой цели  изучена литература по  теме, проанализированы уже доказанные экспериментально факты. Некоторые из них проверены путём измерений и математических расчётов.

 Проведены эксперименты по выявлению пропорций прямоугольников Фехнера и на наличие золотого сечения конкретной  картины. Сконструирован циркуль Фибоначчи и с его помощью произведены измерения. В ходе работы использованы межпредметные связи.

 Работа над данной темой формирует гармоничное представление об окружающем мире, о практической значимости математики.

Список ключевых слов

1.      «Золотое сечение»;

2.      «Золотой прямоугольник»;

3.      «Золотая спираль»;

4.      Циркуль Фибоначчи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Оглавление

 

Введение…………………………………………………………………….............3-5

 

Основная часть

 1. Божественная мера красоты вокруг нас.

 

1.1.            История «золотого сечения»……………………………………………….6

 

1.2.            Понятие «золотое сечение»………………………………………………..6-9

 

1.3.            «Золотое сечение» в живописи……………………………………………9-11

 

1.4.            «Золотое сечение» в природе……………………………………………..11-13

 

 2. Практическая часть.

2.1. Эксперимент по выявлению пропорций прямоугольников Фехнера…….14

2.2. Исследование наличия золотой пропорции в человеческом теле……........14-16

2.3. Исследование картин на наличие золотого сечения…………………….......16

2.4. Циркуль Фибоначчи……………………………………………………...........17

 

Заключение…………………………………………………………………………..18

 

Библиографический список…………………………………………………………19

 

 

 

Введение

                                                                                  Ничто не нравится, кроме красоты,  

                                                                                  в красоте – ничто, кроме форм,
                                                                                  в формах – ничто, кроме пропорций,

                                                             в пропорциях – ничто, кроме числа.

 

                                                                                                       А. Августин

                                                                         

Есть вещи, которые нельзя объяснить. Вот вы подходите к пустой скамейке и садитесь на нее. Где вы сядете — посередине? Или, может быть, с самого края? Нет, скорее всего, не то и не другое. Вы сядете так, что отношение одной части скамейки к другой, относительно вашего тела, будет равно примерно 1,62. Простая вещь, абсолютно инстинктивная... Садясь на скамейку, вы произвели «золотое сечение».

О золотом сечении знали еще в древнем Египте и Вавилоне, в Индии и Китае. Великий Пифагор создал тайную школу, где изучалась мистическая суть «золотого сечения». Евклид применил его, создавая свою геометрию, а Фидий — свои бессмертные скульптуры. Платон рассказывал, что Вселенная устроена согласно «золотому сечению». А Аристотель нашел соответствие «золотого сечения» этическому закону. Высшую гармонию «золотого сечения» будут проповедовать Леонардо да Винчи и Микеланджело, ведь красота и «золотое сечение» — это одно и то же.

Вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле. Неживая природа не знает, что такое «золотое сечение», однако оно используется  в архитектуре и скульптуре, в живописи и математике, в музыке и поэзии…

Моё исследование направлено на выявление связи между многими точными и естественными науками, на формирование представления о «золотом сечении» как средстве познания красоты, порядка и гармонии окружающего мира.

 Объект исследования: «золотое сечение».

Предмет исследования: предметы обихода, архитектуры, живописи, природы, человеческое тело.

Гипотеза: золотое сечение является отображением окружающего мира.

Цель работы: Исследовать, в каких областях жизнедеятельности человека встречается «золотое сечение».

Для достижения своей цели, я выдвинула следующие задачи:

1)      Изучить понятие и историю возникновения золотого сечения.

2)      Рассмотреть применение золотого сечения в различных областях жизнедеятельности человека.

3)      Подобрать материал о ручных инструментах, которые помогают увидеть и изучить золотые пропорции.

4)      Исследовать окружающие предметы обихода, членов моей семьи на соответствие идеальным пропорциям золотого сечения.

5)      Проанализировать полученные результаты и сделать выводы.

Методы исследования: 

1)      теоретический (изучение текстовой информации по данной теме, абстрагирование, анализ, обобщение);

2)      эмпирический (сравнение, сопоставление полученных данных);

3)      математические расчёты пропорциональных отношений;

4)      метод проектов.

Вид проекта: творческий, исследовательский, практико-ориентированный.

Проблема данного исследования носит актуальный характер в современных условиях. Об этом свидетельствует частое изучение вопроса о «золотом сечении» в различных сферах жизнедеятельности человека. Актуальность работы для меня заключается в том, что в ходе исследования расширится моё представление о применении золотой пропорции в жизнедеятельности человека.

Научная значимость работы состоит в оптимизации и упорядочивании существующей научно-методологической базы по исследуемой проблеме.

Практическая значимость темы открытия «золотой пропорции» заключается в её использовании во всех областях жизнедеятельности человека (строительстве, дизайне, живописи, поэзии, бизнесе и т. д)

            Источниками информации для написания работы послужили базовая учебная литература, фундаментальные теоретические труды крупнейших мыслителей в рассматриваемой области, результаты практических исследований видных отечественных и зарубежных авторов, статьи и обзоры в специализированных и периодических изданиях, посвящённых тематике открытия и применения «золотого сечения», справочная литература, прочие актуальные источники информации. Всего в библиографическом списке 14 источников.

            В книге Васютинского Н.А. «Золотая пропорция» в доступной форме  дана информация о золотой пропорции, лежащей в основе гармонии природы и произведений искусства. Рассказано о сути этого замечательного соотношения, истории его открытия и исследований. Описано проявление закономерностей золотой пропорции в архитектуре, музыке, поэзии, а также в химии, биологии, ботанике, геологии, астрономии, технике.

            Основу  книги Ковалёва В. Ф.   «Золотое сечение в живописи» составляет цикл лекций, прочитанных автором  в Киевском государственном художественном институте. Рассматривается множество конкретных примеров применения золотой пропорции в живописи.

Книга Коробко В. И., Коробко Г. Н. «Золотая пропорция и человек» знакомит читателей со многими проявлениями золотого сечения и чисел Фибоначчи в человеке: пропорциях частей тела, физиологических ритмах и функциях организма, оптимальных параметрах внешней среды, эргономике, творчестве (архитектуре, изобразительном и прикладном искусстве, поэзии, музыке, кинематографе и др.). На многочисленных примерах из различных областей знаний о человеке показано, как свойства и закономерности золотого сечения и чисел Фибоначчи проявляются в человеке.     

Планируемый результат: После завершения работы над проектом моё представление о математическом понимании гармонии как соразмерности частей и целого расширится и я смогу связать понятие «золотого сечения» с различными областями жизнедеятельности человека, смогу видеть его примеры вокруг меня, то есть доказать, что математика помогает человеку понять окружающий его мир и воспринять его красоту и гармонию.

Практический результат исследовательской работы:

1)      Презентация «Божественный закон красоты».

2)      Эксперимент по выявлению пропорций прямоугольников Фехнера.

3)      Исследование  наличия золотой пропорции в человеческом теле.

4)      Исследование картин на  наличие золотого сечения. 

5)      Циркуль Фибоначчи.

 

 

  

 

 

 

 

 

 

 

 Основная часть

 1. Божественная мера красоты вокруг нас.

1.1.  История «золотого сечения».

 Историю возникновения и развитие теории о «золотом сечении» можно представить в следующем хронологическом порядке.

VI век

До н.э. считается, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик.

III век

До н. э. впервые встречается в "Началах" Евклида.

Конец 15 –нач.16 веков Леонардо да Винчи ввёл термин "ЗОЛОТОЕ СЕЧЕНИЕ".

1202 математический труд “Книга об абаке” Фибоначчи.

1509 в Венеции издана книга Луки Пачоли “Божественная пропорция” с иллюстрациями предположительно сделанными Леонардо да Винчи.

Эпоха Возрождения широко применяется в науке, искусстве, архитектуре.

1855 немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд “Эстетические исследования”.

Начало 1900-х американский математик Марк Барр (Mark Barr) использовал греческую букву ПСИ (phi) для определения золотой пропорции.

До 1900-х годов термин Phi не применялся, пока американский математик Марк Барр (Mark Barr) не использовал греческую букву ФИ (phi) для определения этой пропорции. К этому времени эта вездесущая пропорция была известна как золотое деление, золотое сечение и золотое соотношение, а также как Божественная пропорция. Phi – первая буква слова-имени Phidias (The Divine Proportion : A Study in Mathematical Beauty by H. E. Huntley), который использовал золотое сечение в своих скульптурах. Phi – это также греческий эквивалент буквы "F", являющейся первой буквой имени Фибоначчи (Fibonacci).

1.2.Понятие «золотое сечение».

В математике пропорцией (лат. proportio) называют равенство двух отношений: a : b= c : d.

Отрезок прямой АВ можно разделить на две части следующими способами:

- на две равные части – АВ : АС= АВ : ВС;

- на две неравные части в любом отношении (такие части пропорции не образуют); Таким образом, когда АВ:АС=АС:ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части,  при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

a : b= b : c или с : b= b : а.

Рис.1.
Геометрическое изображение золотой пропорции.

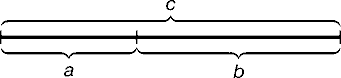
Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

Рис. 2. Деление отрезка прямой по золотому сечению. BC= 1/2 AB; CD= BC

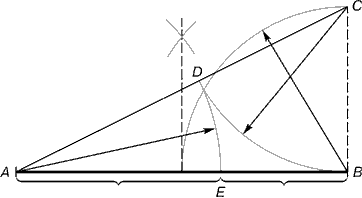
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE= 0,618..., если АВ принять за единицу, ВЕ= 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

Свойства золотого сечения описываются уравнением:

x² – x – 1= 0

Решение этого уравнения:

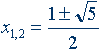
Свойства золотого сечения создали вокруг этого числа романтический ореол таинственности и чуть ли не мистического поклонения.

Для нахождения отрезков золотой пропорции восходящего и нисходящего рядов можно пользоваться пентаграммой.

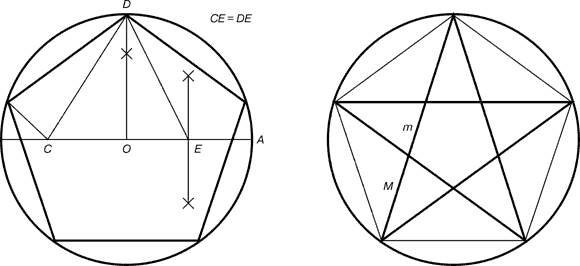
Рис. 3. Построение правильного пятиугольника и пентаграммы.

Для построения пентаграммы необходимо построить правильный пятиугольник. Способ его построения разработал немецкий живописец и график Альбрехт Дюрер (1471...1528). Пусть O – центр окружности, A – точка на окружности и Е – середина отрезка ОА. Перпендикуляр к радиусу ОА, восставленный в точке О, пересекается с окружностью в точке D. Пользуясь циркулем, отложим на диаметре отрезок CE = ED. Длина стороны вписанного в окружность правильного пятиугольника равна DC. Откладываем на окружности отрезки DC и получим пять точек для начертания правильного пятиугольника. Соединяем углы пятиугольника через один диагоналями и получаем пентаграмму. Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией.

Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Рис. 4. Построение золотого треугольника.

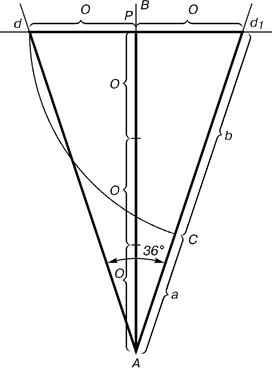Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к линии АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения. Линиями Ad1 и dd1 пользуются для построения «золотого» прямоугольника.(12.)

Построение «золотого прямоугольника».

Вырежьте из бумаги прямоугольник со сторонами 10 см и 16 см. Отрежьте от него квадрат со стороной 10 см. Останется прямоугольник, стороны которого 6 см и 10 см, т. е. одна больше другой тоже примерно в 1,6 раза. Затем от этого прямоугольника отрежьте квадрат со стороной 6см. Останется прямоугольник, одна сторона которого тоже примерно в 1,6 раза больше другой. Этот процесс можно продолжать и дальше.  Форму «золотого сечения» придавали книгам, столам и т.д.   Если провести диагонали первого и второго прямоугольников, то точка их пересечения принадлежит всем получаемым «золотым прямоугольникам».

1.3. «Золотое сечение» в живописи.

Художник, не вооруженный знаниями золотого сечения, всегда будет в плену всяких случайностей и просчетов, которые неминуемо уменьшат художественные достоинства его работ.

При переносе геометрического способа деления на картину или эскиз поступают так: половину длины картины или эскиза откладывают на высоту или продолжение высоты, если эскиз узкого формата. Полученную точку С соединяют с левым нижним углом картины и т. д. (рисунок  5). Линия золотого сечения в левой части картины будет находиться на таком же расстоянии от левого края, как и в правой от правого (показано пунктиром). Указанные выше две пропорции золотого деления — равные величины и неравные, при этом пропорциональные, широко используются в искусстве.

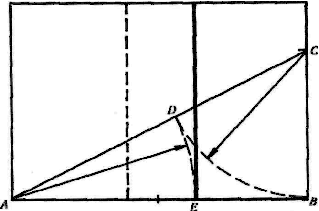
Рисунок 5. Определение линии золотого сечения на картине геометрическим способом.

Если необходимо найти линию золотого сечения на картине или эскизе по горизонтали, то новое деление геометрическим способом высоты картины производить нет необходимости. Достаточно провести диагонали картины. Их пересечения с линиями золотого сечения по вертикали укажут точки, через которые следует провести горизонтальные линии золотого сечения (рисунок 6). Эти линии могут понадобиться при построении пейзажа. Художники-пейзажисты из опыта знают, что нельзя отводить половину плоскости холста под небо или под землю и воду. Лучше брать или больше неба, или больше земли, тогда пейзаж «лучше смотрится».

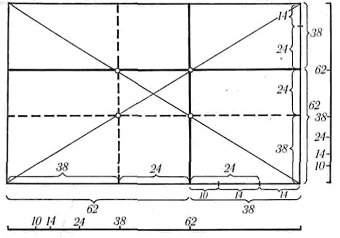
Рисунок 6. Линии золотого сечения и диагонали на картине

 

Из пропорции золотого сечения вытекает, что если высоту или ширину картины разделить на 100 частей, то больший отрезок золотой пропорции равен 62, а меньший — 38 частям. Эти три величины позволяют нам построить нисходящий ряд отрезков золотой пропорции: 100 - 62 = 38; 62 - 38 = 24; 38 - 24=14; 24 - 14=10.

100, 62, 38, 24, 14, 10 — это ряд величин золотой пропорции, выраженных арифметически. Так же находят отрезки золотой пропорции и на картине, если линия золотого сечения по вертикали уже проведена (рисунок 6). Переносим линию золотого сечения в левый край картины. Расстояние между линиями золотого сечения в середине картины равно 24 частям. Отрезок, равный 24 частям, откладываем на отрезок, равный 38 частям, и получаем остаток, равный 14 частям. Последний отрезок накладываем на отрезок, равный 24 частям, и получаем отрезок, равный 10 частям. Все отрезки нисходящего ряда золотой пропорции для данной картины мы получили. Ту же операцию проводим и с высотой картины. Полученные отрезки переносим на полоску плотной бумаги или картона — для ширины с лицевой стороны и для высоты с оборотной. Этот простейший инструмент назовем пропорциональной линейкой. Такая пропорциональная линейка пригодна только для данного эскиза или эскиза такого же размера. Изготовление ее занимает несколько минут, но в дальнейшем облегчит работу над эскизом в поисках интервалов между фигурами или группами фигур, между предметами, поможет найти их размеры и, в конечном итоге, гармонизовать линейное построение картины.

 1.4 «Золотое сечение»  в природе.

            Характерной чертой строения растений и их развития является спиральность. Еще Гете, который был не только великим поэтом, но и естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. Спирально закручиваются усики растений, по спирали происходит рост ткани в стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно,  в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровнях.

            Существует несколько способов листорасположения. В первом  листья побега располагаются строго один под другим, образуя вертикальные ряды – ортостихи. Условная спираль, соединяющая места расположения листьев на побеге, называется генетической, или основной спиралью, точнее, винтовой линией и делится на ряд листовых циклов. Генетическим этот винт называется потому, что расположение листьев в нем отвечает порядку появления в нем листьев. Проекция на плоскость листорасположения позволяет в долях окружности выразить угол расхождения листьев.

            Винтовое расположение листьев выражают дробью, числитель которой равен числу оборотов по стеблю воображаемого винта одного листового цикла, а знаменатель -  числу листьев в данном цикле, совпадающему с числом ортостих на стебле. Эта дробь позволяет рассчитать и угол расхождения листьев.

            Оказалось, что каждое растение  характеризуется своим листорасположением. Так у липы, вяза, бука, злаков листорасположение описывается формулой 1/2, у дуба и вишни – 2/5, у малины, груши, тополя, барбариса – 3/8, у миндаля, облепихи – 5/13 и т.д. Нетрудно видеть, что в формулах листорасположения встречаются числа Фибоначчи, расположенные через одно.

            Посмотрим на сосновую шишку. Чешуйки на ее поверхности расположены строго закономерно -  по двум спиралям, которые пересекаются приблизительно под прямым углом. Число таких спиралей у сосновых шишек равно 8 и 13  или 13 и 21 . Такие же спирали видны в поперечных разрезах почек; здесь числа спиралей относятся как  числа 3/5, 5/8, 8/13. В корзинках подсолнечника семена также расположены по    двум спиралям, их число составляет обычно 34 и 55, 55 и 89. Здесь вновь мы видим закономерное сочетание чисел Фибоначчи, расположенных рядом: 2/3, 3/5, 5/8, 13/21 и т.д. Их отношение в пределе стремится к числу j = 0,61803…

            Рассмотренную закономерность расположения листьев, чешуек, семян называют филлотаксисом.

             Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНК закручена двойной спиралью. Гете называл спираль «кривой жизни». Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.

Рисунок 7. Цикорий.

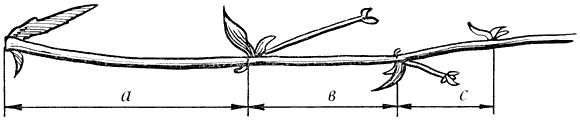
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

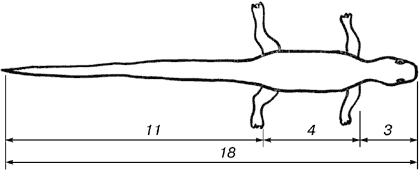
Рисунок 8. Ящерица живородящая.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.

Рисунок 9. Золотые пропорции в частях тела человека.

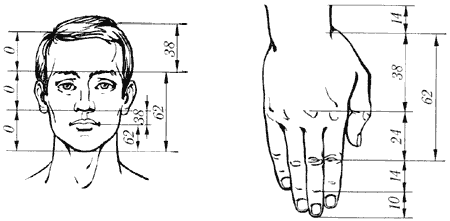
Рисунок 10. Золотые пропорции в фигуре человека.

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

 

 2. Результаты исследования.

2.1.  Эксперимент по выявлению пропорций прямоугольников Фехнера.

    Прямоугольники Фехнера  могут ассоциироваться с самыми различными реальными объектами — форматы картин, поля фасадов зданий, форматы поздравительных открыток или буклетов и т.д. Прямоугольники «вытянуты» как по горизонтали, так и по вертикали. Предлагается, опираясь на свое внутреннее интуитивное ощущение, выбрать прямоугольники, имеющие пропорции, наиболее приятные для глаза. Одним из них был "золотой" прямоугольник с отношением сторон 21:34 (что весьма близко к "золотому" прямоугольнику). Испытуемым предлагалось посредством сравнения упорядочить прямоугольники по степени привлекательности для восприятия, отобрав один из прямоугольников, наиболее удовлетворяющих "эстетическому критерию".

Я провела исследование среди учащихся 6 класса (12 человек), 9 класса (19 человек) и  среди некоторых учителей нашей школы (8 человек).   Вот результаты эксперимента: «золотой» прямоугольник выбрали 2 человека из 6 класса (16,6%); 8 учащихся 9 класса (42,1%); 6 учителей (75%).

Опыты оказались чрезвычайно благоприятными для "золотого" прямоугольника.  Можно сделать заключение, что, по-видимому, ощущение прекрасного в его наиболее тонких и глубоких сторонах присуще больше человеку зрелому.

2.2.  Исследование наличия золотой пропорции в человеческом теле.

Я провела необходимые измерения  тела своей подруги, чтобы доказать, что человеческое тело подчинено закону золотого сечения.  

№ п/п	Измерения и вычисления	Результат
1.	Полный рост (см)	163
2.	Расстояние от пупка до подошвы (см)	101
1:2	163:101	1,61 Золотое сечение есть
3.	Расстояние от макушки головы до пупка (см)	62
2:3	101:62	1,62 Золотое сечение есть
4.	Расстояние от макушки головы до кончиков рук (см)	95
5.	Расстояние от кончиков пальцев и до стопы (см)	68
3:4	95:68	1,39 Золотое сечение отсутствует
6.	Расстояние от плеча до локтя (см)	27
7.	Расстояние от локтя до кончиков пальцев   (см)	43
7:6	43:27	1,59 Близко к золотому сечению
8.	Расстояние от локтя до начала кисти руки (см)	26,5
7:8.	43:26,5	1,62 Золотое сечение есть
9.	Расстояние от начала кисти руки до кончиков пальцев (см)	16,5
8:9	26,5:16,5	1,60 Золотое сечение есть
10.	Вся голова (см)	22,5
11.	Расстояние от бровей до подбородка (см)	14
12.	Расстояние от макушки головы до бровей (см)	8,5
10:11	22,5:14	1,65 Золотое сечение есть
11:12	14:8,5	1,64 Золотое сечение есть
13.	Расстояние от кончика носа до подбородка (см)	5,2
14.	Расстояние от губ до подбородка (см)	3,2
15.	Расстояние от кончика носа до губ (см)	2
13:14	5,2:3.2	1,62 Золотое сечение есть
14:15	3,2:2	1,60 Золотое сечение есть
16.	Расстояние от начала кисти руки и до конца первого фаланга пальцев (см)	13
17.	Расстояние от начала кисти руки до костяшек (см)	8
18.	Расстояние от костяшек до конца первого фаланга (см)	5
16:17	13:8	1,62 Золотое сечение есть
17:18	8:5	1,60 Золотое сечение есть

 

 Выполнив измерения, можно убедиться, что не все части человеческого тела имеют пропорции золотого сечения.

2.3.  Исследование картин на наличие золотого сечения.

Предмет исследования – картина, подаренная выпускниками школы. Она висит на стене коридора нашей школы.

Замысел картины: Летний пейзаж. Река, через которую перекинут кирпичный мостик.

Формат картины: длина 800мм, ширина 500мм.

Путем вычисления я находила величину отрезков нисходящего ряда золотой пропорции. Зная ширину или высоту репродукции, можно легко их проанализировать. Для этого я брала всю ширину или высоту, как 100 частей. Затем находила от нее 1 сотую часть. После этого получившееся значение умножала на соответствующую величину золотой пропорции - 62, 38, 24, 14, 10, 4. Произведения я представляла в буквенных значениях:

62 части – a=496мм по длине, 310мм по ширине

38 частей – b=304мм по длине, 190мм по ширине

24 части – c=192мм по длине, 120мм по ширине

14 частей – d=112мм по длине, 70мм по ширине

10 части – e=80мм по длине, 50мм по ширине

4 части – f=32мм по длине, 20мм по ширине

Результат откладывала на картине с помощью нити. Оказалось, расположение объектов и их величина на картине является не случайным. Мост расположен на линии золотого сечения. Происходит чередование равных (природа по краям картины) и неравных (облака вверху и река внизу) величин в пропорции золотого сечения.   Все это создает гармоничное восприятие картины.

 

 

2.4. Циркуль Фибоначчи.

Но может быть «золотое сечение» забыто, и в наши дни совсем не используется современными дизайнерами, художниками, архитекторами? Как  же это проверить? Я решила создать свой инструмент для определения «золотой пропорции». Мой циркуль помог  сделать мне дедушка.   Мы взяли четыре деревянные рейки следующих размеров: две по 340 мм, одну 210 мм и одну длиной 80 мм. Просверлили в больших  рейках отверстия и соединили с рейками поменьше шурупами (Приложение 1). Отношения длин отрезков  равно золотому сечению (1,61). Этот циркуль  позволит  выбрать правильный дом, в котором есть золотое сечение, ковёр, бассейн..  да что угодно.

Я с помощью циркуля проверила соотношения золотых пропорций на теле своих друзей. Установила с его помощью, что комод сделан с учётом золотых пропорций. Упаковка масла сливочного – золотой прямоугольник.

Таким образом, существуют несложные инструменты измерения пропорций золотого сечения, пользуясь которыми, можно с уверенностью сказать о гармоничном содержании измеряемых объектов нашей жизни.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Заключение

Всегда интересно познавать что-то новое, открывать для себя то, что может быть увлекательным. Такой стала для меня эта работа.

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы.

Таким образом, в ходе моей работы я изучила литературу по данному вопросу, познакомилась с произведениями искусства и пришла к выводам:

- Форма, в основе построения которой лежит закон «золотого сечения», способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии.

- Золотая пропорция – понятие математическое. Но она является критерием гармонии и красоты, а это уже категории искусства.

- Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому.

- Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве,   природе, окружающем нас мире.

- Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.

- Законам «Золотого сечения», то есть абсолютной гармонии, подчиняются не только плоды человеческой деятельности, но и сам человек — его внутренние органы и системы, его душа, его мысли.

- С рождения человеку предписано находиться в гармонии с собой и с внешним миром. Как только эта гармония нарушается, человек «выпадает» из универсальных структур мироздания, сотворенных неведомым и загадочным Вселенским Разумом. У человека начинаются всевозможные проблемы. И прежде всего — проблемы со здоровьем, поскольку болезнь есть не что иное, как отклонение от классических пропорций, дарованных природой.
 Метод «Золотого сечения» каждому по силам. Он доступен и эффективен, несмотря на свою простоту.

Действительно, «золотое сечение» - драгоценный камень.

 

 

Библиографический список

 

1.      Азевич Н. А. Двадцать уроков Гармонии - М., Школа-Пресс, 1998

2.      Брунов Н. Пропорция античной и средневековой архитектуры - М., Издательство Всесоюзной академии архитектуры, 1936

3.      Васютинский Н. А. Золотая пропорция - М., Молодая гвардия, 1990

4.      Волошинов А. В. Математика и искусство - М., Просвещение, 1992

5.      Волошинов А. В. Пифагор - М., Просвещение, 1992

6.      Глейзер Г. И. История математики в школе 7-8 класс - М., Просвещение, 1980

7.      Ковалев Ф. В. Золотое сечение в живописи - М., Высшая школа, 1989

8.      Коробко В. И., Коробко Г. Н. Золотая пропорция и человек – «АСВ» 2002

9.      Литвиненко А. А. Энергия пирамид. Волшебный прут и звездный маятник – М. Провит-стайл, 2004

10.   Приложение к газете «Первое сентября» №24, 31, 45, 48 – 2001 г; № 45, 36 – 2002 г.; № 42, 8 – 2003 г.; № 24 – 2004 г.

11.  Стахов А.П. Гармония Мироздания и Золотое Сечение: древнейшая научная парадигма и ее роль в современной науке, математике и образовании.// http://www.trinitas.ru/rus/002/a0232001.htm

12.  Шарыгин Н. Ф. Наглядная геометрия – М., 1992

13.  Шевелев и. И., Марутаев М. А., Шмелев И. П. Золотое сечение – М., Стройиздат, 1990

14.   Энциклопедический словарь юного математика – М.. 1989