Исследовательская работа "Латинский крест"

IV Открытая Региональная научно- практическая конференция

 «Наука. Образование. Профессия»

Площадка:  научно-техническая

Куб и латинский крест

Автор работы

Назаргалина  Юлия Раисовна

ученица  9 б класса

МАОУ «Лицей №1»

 городского округа город Стерлитамак

 Республики Башкортостан

Руководитель 

Сологуб Оксана Викторовна

учитель математики

МАОУ «Лицей №1»

 городского округа город Стерлитамак

 Республики Башкортостан

г. Стерлитамак

2015

Содержание

1.     Введение

2.     Немного теории

2.1.          Развертка куба

2.2.          Куб

2.3.          Куб 4Д

2.4.          Трехмерная развертка четырехмерного куба

3.     Практическое применение

4.     Мои эксперименты

5.     Итоги работы

6.     Использованная литература

7.     Приложения

8.     Тезисы

1.     Введение

Однажды я увидела по телевизору, как из развертки куба получилась совсем другая фигура. Обзор литературы по этому вопросу привел к тому, что данная тема разрабатывается совсем недавно, с 2000 годов, но вклад в эту работу внесли такие ученые как Леонард Эйлер (теорема о соотношении между количеством ребер, вершин и граней в многограннике), Огюстен Коши (теорема которого утверждает, что если из данных плоских многоугольников, взятых в одинаковом порядке, можно склеить выпуклый многогранник, то он будет единственным) и Александр Данилович Александров, который в своей теореме сообщил о необходимых и достаточных условиях, при которых из развертки можно получить выпуклый многогранник.

Меня заинтересовал этот материал, поэтому я задалась вопросом: сколько существует фигур (многогранников), которые получаются из развертки куба?

Цель исследования:

Узнать о развёртках куба, свойствах  куба, как его сконструировать, возможности применения развертки куба  в практических целях.

Задачи:

1) Изучить  развертку куба и его свойства.

2) Наиболее подробно описать «что такое куб»

3) Сконструировать модель куба разными способами.

4) Практическое применение развертки куба.

2.     Основная часть

В процессе изучения литературы, выяснилось, что уже создано огромное количество программ, которые рисуют развертки фигур из латинского креста, в частности, меня заинтересовала работа группы  Эрика Демиана. Они написали программу, которая выдала 85 разверток многогранников   латинского креста.

В ходе складывания их фигур  выявились некоторые недостатки: не все линии были представлены на рисунках и их приходилось делать самим.  А некоторые развертки, которые мы старались придумать сам, уже были ими придуманы,  и нам осталось их только склеить.

Немного теории

2.1.     Развертка куба

Если разрезать бумажный куб вдоль ребер так, чтобы его можно было разогнуть и положить всеми 6-ю квадратами на стол, то получим фигуру вроде трех следующих:

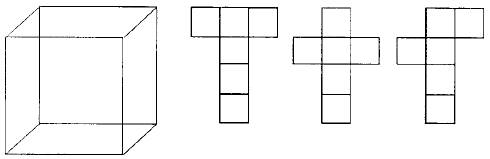
Любопытно сосчитать: сколько различных фигур можно получить таким путем? Другими словами, сколькими способами можно развернуть куб на плоскости? Различными условимся считать две развертки, которые не совпадают при

наложении друг с другом или одной из них с ее зеркальным отражением.

2.2.                     Куб  - это один из видов правильных многогранников, так называемых Платоновых тел. Этот многогранник является правильным, так как, во-первых, имеет каждую грань в виде квадрата, и все они — одного размера. Во-вторых, все ребра куба одинаковы. В-третьих, внутренние углы между его смежными гранями равны. У куба такой  угол равен 90 градусам. В-четвертых, куб, как и каждое из Платоновых тел может быть вписан в сферу, каждой своей вершиной касаясь поверхности этой сферы. Кубы бывают разного размера, они могут быть изготовлены из разных материалов, но они имеют одну и ту же форму, так называемую модель куба.

Свойства куба

В куб можно вписать тетраэдр двумя способами, притом четыре вершины тетраэдра будут совмещены с  четырьмя  вершинами  куба.  Все  шесть  рёбер  тетраэдра  будут  лежать  на  всех  шести  гранях куба и равны диагонали грани-квадрата.

Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно  четырём  его  главным  диагоналям.

В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба.

Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра.

В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно  на  шести  гранях  куба, остальные  24 ребра  —  внутри   куба.  Все   двенадцать   вершин   икосаэдра   будут   лежать  на  шести  гранях  куба.

Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную.

Модель куба участвует в таких играх и головоломках «для всех» как кубики сома, кубик Рубика, кубики Сонобе. Конструирование модели куба разными способами, тренирует терпение и пространственное мышление.

2.3.     Куб, 4D

Мы живём в трехмерном мире, но пространства других размерностей тоже используем. Например, двумерное пространство: широта и долгота при перемещении по поверхности планеты, ряд и кресло в театре, и т.д. Объемную фигуру (3D) можно развернуть на плоскость (2D). Так куб превращается в 4 квадрата. Точнее, не куб, а его поверхность.

А вот как выглядит трехмерная развертка четырехмерного куба?

Мы можем  "сгибание в 4е измерение", но увидеть его мы не в наших  силах, как и для жителей двумерного пространства, которые  не смогут понять, что значит что-то "согнуть вдоль ребра", для них видно только то,  что боковой квадрат исчезает (входит внутрь стенки)

Но если  (как это делается с "изображением" тессеракта) искусственно ввести изменение масштаба при движении вдоль четвертой оси. По аналогии с перспективным изображением трехмерного куба в виде вложенного в себя уменьшенного квадрата (самый последний чертеж под катом) можно вложить в себя трехмерную уменьшенную копию куба. Но это не 4х мерный куб, а схематичное изображение (граф связности вершин). При вычислении суммарного объема надо помнить, что объем исходного куба равен объему вложенной копии и объемам шести боковых усеченных пирамид. Получаем объемы в объеме и т.д. Без масштабных искажений не увидеть пирамид — они размажутся по боковой стенке, а копия наложится точно на исходный куб и поэтому тоже будет не видна.

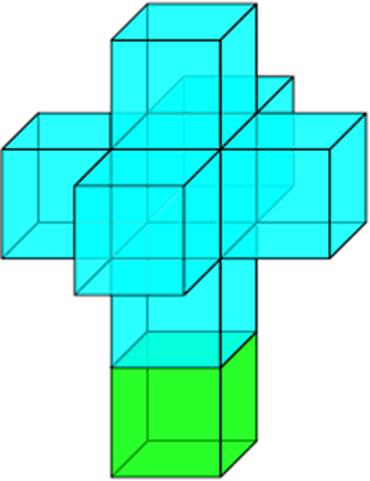
2.4.     Трехмерная развертка четырехмерного куба

Всего кубиков 8, центральный кубик почти не виден, он спрятан. Построение 4-мерного куба сводится к "сгибанию" через боковые квадраты шести кубиков в центр, затем туда же дополнительный кубик. Мы результат не увидим, для жителей трехмерного мира все дополнительные кубики "провалятся" внутрь центрального. Также как при сгибании двумерной развертки на плоскости остается один квадрат, остальные уходят в третье измерение. Вот такая геометрическая забава. Куба нет, а развертка есть.

3.     Практическое применение кубиков, кубов, разверток

Модель куба участвует в таких играх и головоломках «для всех» как кубики сома, кубик Рубика, кубики Сонобе. Конструирование модели куба разными способами, тренирует терпение и пространственное мышление.

Кубики сома  состоят из семи элементов, составленных из 27 кубиков. Шесть элементов составлены из четырёх кубиков, один – из трёх. Элементы представляют собой «неправильные» фигуры, в том смысле, что на них имеются выступы и впадины. Из них можно собрать не только куб, но и много других вполне симметричных фигур.  

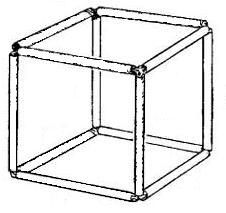
Интересную головоломку придумал  Говард Флейшер.  Рецепт её изготовления крайне прост, и сделать её может каждый. Всё, что для этого нужно, это 12 соломок (трубочек, авторучек, корпусы пустых фломастеров) одинаковой длины и нитка или кусок авиамодельной резинки. Далее соедините трубочки так, что бы получился куб.

Тессеракт  — четырёхмерный гиперкуб — куб в четырёхмерном пространстве.

Согласно Оксфордскому словарю, слово tesseract было придумано и начато использоваться в 1888 Чарльзом Говардом Хинтоном (1853—1907) в его книге «Новая эра мысли». Позже некоторые люди назвали ту же самую фигуру тетракубом — четырёхмерным кубом.

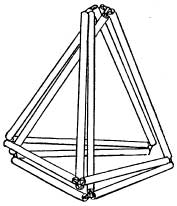
Таким образом, на основе модели куба можно создать не только различные головоломки, но и плоские геометрические фигуры и многогранники.

Если рассмотреть плоскость любой грани, то многогранник должен будет в одном полупространстве относительно плоскости грани многогранника.

4.     Мои эксперименты

В школе, конечно, изучают фигуру куб, но мы нашли работы группы  Эрика Демиана. Они написали программу, которая выдала 85 разверток многогранников   латинского креста. (Приложение 1)

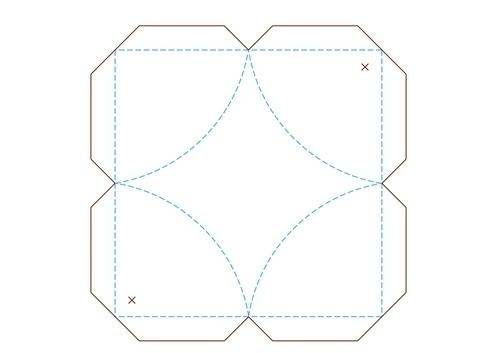
 (Моя развертка куба, из которой получились фигуры, представленные ниже)

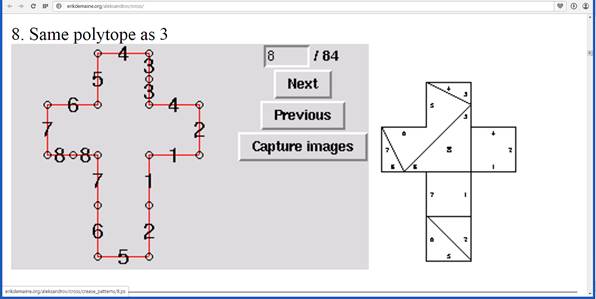
Что получилось по программе команды Эрика Демиана

Практическая часть заключается в том, что мы из  одной и той же развертки  получили 3 совершенно различные фигуры, по схеме математических этюдов. По схемам, представленным в программе мы склеили и получили фигуры.

Пошаговая инструкция:

1. Распечатать шаблоны развертки куба.

 2. Аккуратно вырезать схему куба.

3. Отметить, где надо, середины сторон и соединить линии.

4. Согнуть вырезанный шаблон куба по линиям

5. Смазать затемненные участки клеем и сторону за стороной собрать весь куб.

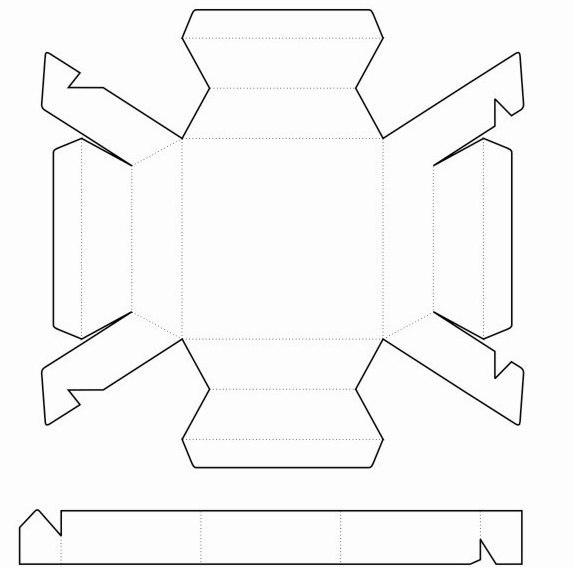
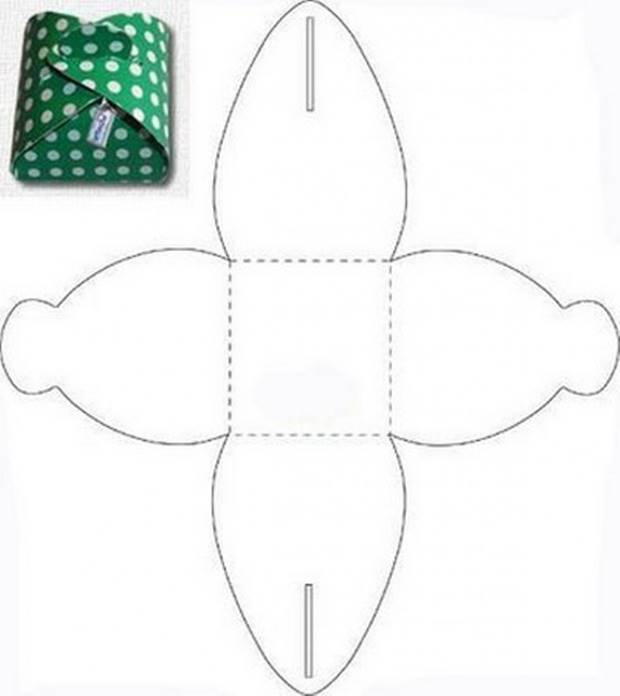
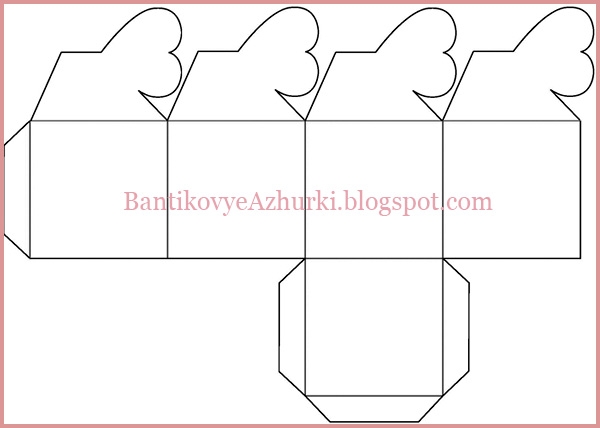
В приложении 2 показаны шаблоны и развертки нескольких фигур, в основе которых лежит квадрат.

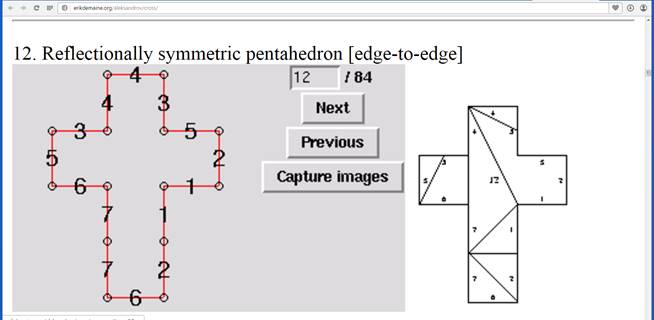
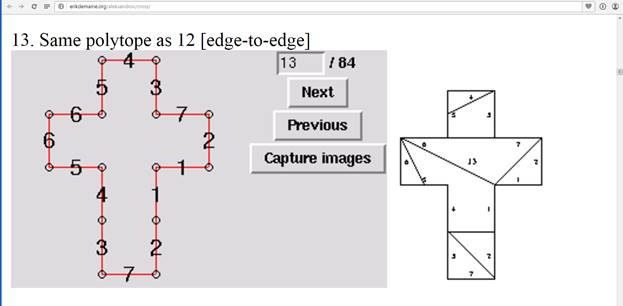
5.     В результате исследования мне удалось:

·       изучить куб и узнать многие его свойства;

·       наиболее подробно описать «что такое куб» - его состав и элементы;

·       углубить знания, полученные на уроке, расширить общий кругозор в ходе решения различных практических задач и изучения интересных фактов из истории математики;

·       какие бы программы не были созданы человеком, процесс творчества, фантазия человека не заменит никакая программа.

Вывод:  по моему мнению, самой увлекательной стороной применения куба,  его развертки является конструирование из него объёмных моделей. Например, различные коробочки для упаковки предметов бытовой техники, лампочек, тортов, печенья, конфет.

Приложение 1

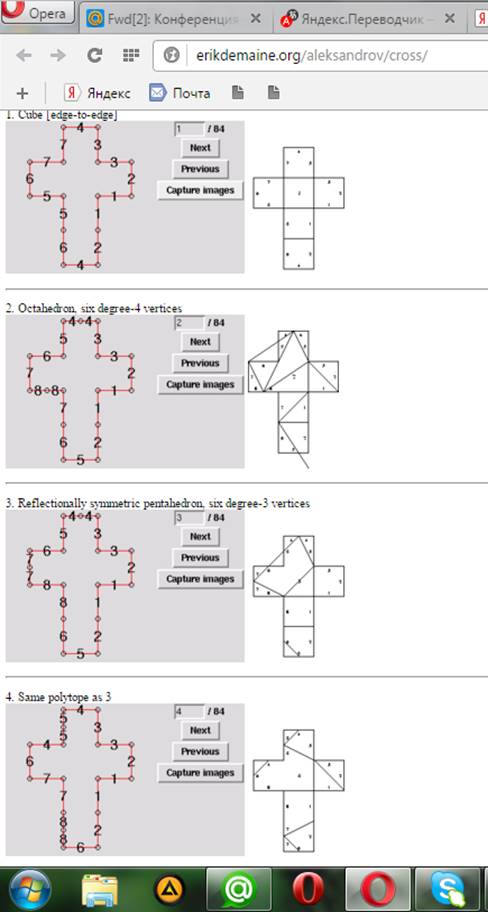
Приложение 2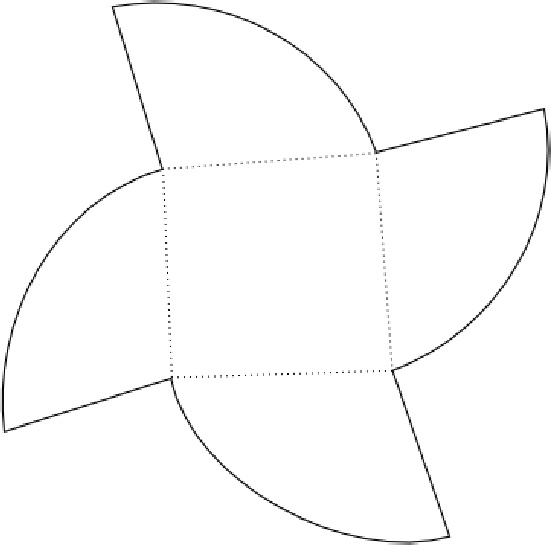  

7.     Используемая литература.

1. М. Гарднер, «Математические головоломки и развлечения» - М., Мир, 1971 г.

2. А. Г. Мордкович, В. А. Гусев. Справочник школьника. Математика. – АСТ, Астрель, 2008 г.

3. С. Ф. Быльцов, «Занимательная математика для всех». – Питер, 2005 г.

4. «Большая иллюстрированная энциклопедия школьника», М., Махаон, 2007г.

5.  А. Д. Александров. Выпуклые многогранники.

6. Anna Lubiw, Joseph O'Rourke. When Does a Polygon Fold to a Polytope E. Demaine. 85 вариантов сложения латинского креста

7. Н. П. Долбилин. Три теоремы о выпуклых многогранниках.   Часть 1 // Квант. 2001. N 5. С. 7—12.   Часть 2 // Квант. 2001. N 6. С. 3—10.

8. Тезисы работы

Куб и латинский крест

Однажды я увидела по телевизору, как из развертки куба получилась совсем другая фигура. Обзор литературы по этому вопросу привел к тому, что данная тема разрабатывается совсем недавно, с 2000 годов, но вклад в эту работу внесли такие ученые как Леонард Эйлер (теорема о соотношении между количеством ребер, вершин и граней в многограннике), Огюстен Коши (теорема которого утверждает, что если из данных плоских многоугольников, взятых в одинаковом порядке, можно склеить выпуклый многогранник, то он будет единственным) и Александр Данилович Александров, который в своей теореме сообщил о необходимых и достаточных условиях, при которых из развертки можно получить выпуклый многогранник.

Меня заинтересовал этот материал, поэтому я задалась вопросом: сколько существует фигур (многогранников), которые получаются из развертки куба?

В процессе изучения литературы, выяснилось, что уже создано огромное количество программ, которые рисуют развертки фигур из латинского креста, в частности, меня заинтересовала работа группы  Эрика Демиана. Они написали программу, которая выдала 85 разверток многогранников   латинского креста.

         В ходе складывания их фигур  выявились некоторые недостатки: не все линии были представлены на рисунках и их приходилось делать самим.  А некоторые развертки, которые мы старались придумать сам, уже были ими придуманы,  и нам осталось их только склеить.

         В ходе работы я познакомилась с теоремами Коши, Эйлера и Александрова А.Д., каждая из которых дополняет другую.  И решила попробовать сложить из разверток других фигур новые. Что получилось – в приложениях к моей работе.

Скачано с www.znanio.ru