Применение графического метода
при решении текстовых
задач на движение
Цель работы:
Разработать и применить графический
метод
к решению текстовых задач на движение.
Задачи:
1) Ознакомиться с понятием графического
метода.
2) Использовать графический метод в
решении текстовых задач на движение.
3) Провести сравнительный анализ решения
задач алгебраическим и графическим
методами.
метод подобия
соотношения
между сторонами
и углами
прямоугольного
треугольника
Графический
метод
Составление
графической
модели ситуации
движения
определение и
свойства средней
линии
треугольника
последовательные
умозаключения,
основанные на
исследовании
относительного
движения
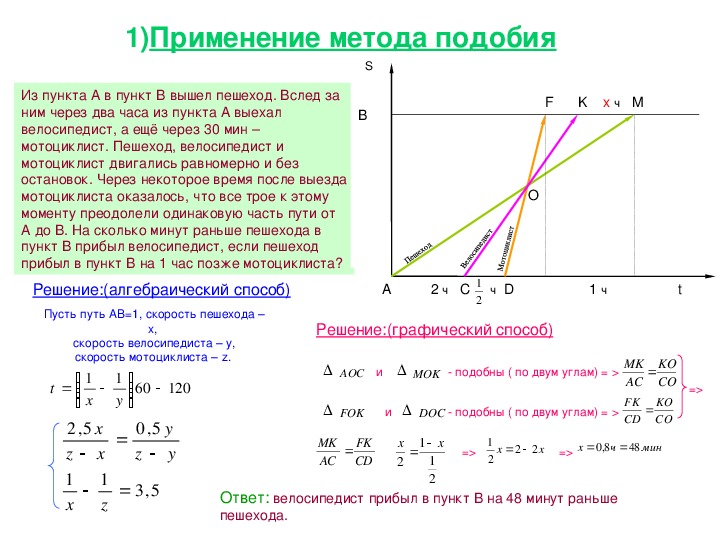
1)Применение метода подобия
Из пункта А в пункт В вышел пешеход. Вслед за
ним через два часа из пункта А выехал
велосипедист, а ещё через 30 мин –
мотоциклист. Пешеход, велосипедист и
мотоциклист двигались равномерно и без
остановок. Через некоторое время после выезда
мотоциклиста оказалось, что все трое к этому
моменту преодолели одинаковую часть пути от
А до В. На сколько минут раньше пешехода в
пункт В прибыл велосипедист, если пешеход
прибыл в пункт В на 1 час позже мотоциклиста?
Решение:(алгебраический способ)
Пусть путь АВ=1, скорость пешехода –
x,
S
B
F K x ч M
O
A 2 ч С ч D 1 ч t
1
2
t
1
y
60
120
скорость велосипедиста – y,
скорость мотоциклиста – z.
1
x
5,2
z
1
x
x
x
1
z
5,0
z
y
y
5,3
Решение:(графический способ)
AOC
и
MOK
подобны ( по двум углам) = >
FOK
и
DOC
подобны ( по двум углам) = >
MK
AC
FK
CD
KO
CO
KO
CO
=>
MK
AC
FK
CD
=>
1
2
1
x
2
x
1
2
x
22
x
x
=>
8,0
ч
48
мин
Ответ: велосипедист прибыл в пункт В на 48 минут раньше
пешехода.
S,к
м
B
S
2
N
S
2
А
2) Применение определения и свойства
средней линии треугольника
2 ч C
E x ч
O
S
4
F
Два поезда отправляются из пунктов
А и В навстречу друг другу. Они
встретятся на половине пути, если
поезд из А выйдет на 2 часа раньше,
чем поезд из В. Если же оба поезда
выйдут одновременно, то через 2
часа расстояние между ними
составит 0,25 расстояния между А и
В. За какое время каждый поезд
проходит весь путь?
K L M t,ч
Решение:
OEF
и
ONA
подобны ( по двум углам) =
>
EO
NO
EF
NA
=>
x
x
2
NE
NO
NE–
линия
4
EO
средняя
–
NO
линия
ABL =>
средняя
AL
NE
2
ABC =>
4
Ответ: поезд из А проходит весь путь за 8 часов, из В – за
4 часа.
1
4
1
2
= >
2x
S
S
BC
NO
8
2
3) Применение соотношения между сторонами
и углами прямоугольного треугольника
( тангенс острого угла )
S,км
B
A t,ч
t
t
1
2
t
1
2
1
2
Решение:
Обозначим
мv
скорость машины,
аv
скорость автобуса
OCF
и
OSK
прямоугольные,
KS
FC
v
v
м
а
tg
tg
FC
OC
:
FC
OS
t
FC
2
FC
1
2
t
Ответ: машина проходит путь от А до В в 2 раза быстрее, чем автобус.
K
S
Пассажир, едущий из А в В,
одну половину затраченного
на путь времени ехал на
автобусе, а вторую – на
автомашине. Если бы он ехал
от А до В только на автобусе,
то это заняло бы в полтора
раза больше времени. Во
сколько
быстрее
проходит путь от А до В
машина, чем автобус?
раз
O
C
F
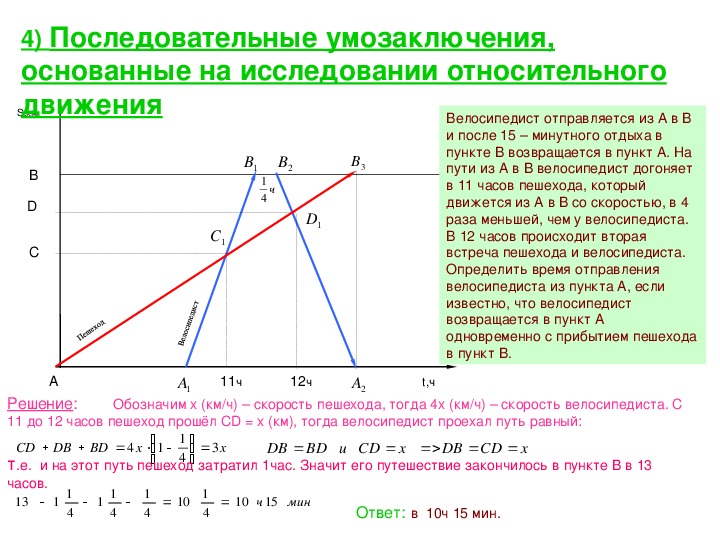
4) Последовательные умозаключения,
основанные на исследовании относительного
движения
S,км
3В
1В
2В
1
4
ч
1D
1С
B
D
C
Велосипедист отправляется из А в В
и после 15 – минутного отдыха в
пункте В возвращается в пункт А. На
пути из А в В велосипедист догоняет
в 11 часов пешехода, который
движется из А в В со скоростью, в 4
раза меньшей, чем у велосипедиста.
В 12 часов происходит вторая
встреча пешехода и велосипедиста.
Определить время отправления
велосипедиста из пункта А, если
известно, что велосипедист
возвращается в пункт А
одновременно с прибытием пешехода
в пункт В.
A 11ч 12ч t,ч
2А
1А
Решение: Обозначим x (км/ч) – скорость пешехода, тогда 4x (км/ч) – скорость велосипедиста. C
11 до 12 часов пешеход прошёл CD = x (км), тогда велосипедист проехал путь равный:
1
4
1
4
x
BD
DB
CD
т.е. и на этот путь пешеход затратил 1час. Значит его путешествие закончилось в пункте В в 13
часов.
13
мин
ч 15
10
10
3
x
CD
BD
DB
DB
CD
x
x
1
и
1
1
4
1
4
1
4
1
4
Ответ: в 10ч 15 мин.
"Вдвойне делает тот,
кто делает скоро !"
" Bis dat, qui cito dat ! "
