
Классификация дифференциальных уравнений в частных производных второго порядка
Общий вид функции u (x1, x2, …, xn) в области Д.
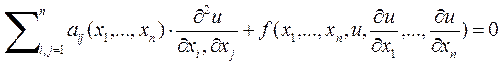 (1)
(1)
aij – функции, заданные в области Д;
aij, f – вещественные функции;
aij=aji
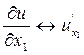
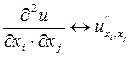
Зафиксируем определённую
точку ![]() в области Д и составим
следующее:
в области Д и составим
следующее:
1)
квадратичную форму 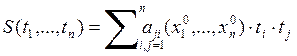 (2)
(2)
2)
линейные преобразования 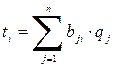
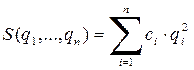 (3)
(3)
3) классификация: если все коэффициенты квадратичной формы уравнения (3) положительные или все отрицательные, то уравнение (1) принадлежит эллиптическому типу в точке М.
Если все коэффициенты ci в уравнении (3) кроме одного имеют определённый знак, а оставшийся один имеет противоположный знак, то уравнение (1) принадлежит гиперболическому типу в точке М.
Если квадратичная форма уравнения (3) имеет только один коэффициент ci=0, а все остальные коэффициенты имеют одинаковый знак, то уравнение (1) принадлежит параболическому типу.
Уравнение (1) принадлежит определённому типу в области Д, если во всех точках этой области она принадлежит этому типу.
Пусть задана функция u(x,y).
Линейное дифференциальное уравнение: 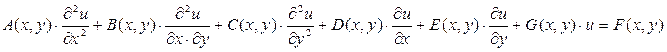
Уравнение называется
линейным, если оно линейно относительно неизвестной функции и её частных
производных. Для функции двух переменных канонические формы будут выглядеть
следующим образом ![]()
1)
гиперболический тип: 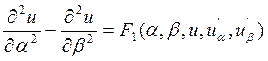
2)
эллиптический тип: 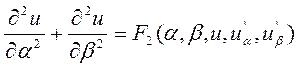
3)
параболический тип: 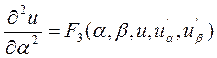
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.