Конформные отображения. Дробно-линейная функция

Определение 1. Функция вида

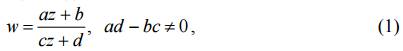
где a, b, c, d – комплексные числа, называется дробно-линейной.

Отображение, задаваемое этой функцией, называется дробно- линейным.

Условие  ad − bc ≠ 0 означает, что w ≠ const . Функция (1) осуществляет конформное отображение расширенной комплексной плоскости Z на расширенную комплексную плоскость w, так как производная

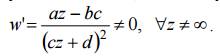
Для 0 c ≠ предполагаем, что

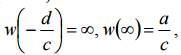
для  c = 0 функция (1) становится линейной, т. е. w = az + b и w(∞) = ∞. Функция

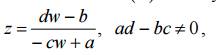
является обратной к функции (1). Она также является дробно-линейной и однозначной на расширенной комплексной плоскости, т. е. здесь функция (1) является однолистной.

Каждое дробно-линейное отображение может быть получено в результате последовательного выполнения трех отображений: линейного, отображения w = 1/z и снова линейного отображения.

Дробно-линейные отображения переводят:

1) окружность или прямую в окружность или прямую (круговое свойство);

2) пару точек, симметричных относительно окружности, – в пару то- чек, симметричных относительно образа этой окружности (свойство сохранения симметрии). Здесь "окружность", в частности, может быть прямой, если под последней понимать окружность бесконечного радиуса.

Существует единственное дробно-линейное отображение, которое три разных точки  z₁, z₂, z₃ переводит соответственно в три разные точки  w₁, w₂, w₃. Это отображение задается формулой

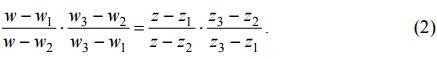
Если одна из точек z_k или w_k (k =1, 2, 3) является бесконечно удаленной точкой, то в формуле (2) разности, в которые входит z_k или w_k, требуется заменить единицами.

Существует бесконечно много дробно-линейных отображений, которые заданную окружность γ отображают на заданную окружность Г, причем область D, для которой γ является границей, отображается на одну из областей, для которой Г является границей.

Для обеспечения единственности дробно-линейного отображения достаточно выполнение одного из условий:

1) заданная точка z₀ ∈ D отображается в заданную точку  w₀ ∈ D', а любая кривая, выходящая из точки z₀, поворачивается на заданный угол α w₀ = f (z₀), α = arg(f '(z₀));

2) точки z₀ ∈ D и z₁ ∈ γ отображаются соответственно в заданные точки w₀ ∈ D'  и w₁ ∈ Γ.

Пример 1. Найти образ окружности, заданной уравнением

x² + y² + 2x − 4y + 1 = 0,

при отображении w  = 1/z.

Решение. На основании кругового свойства дробно-линейного отображения окружность переходит в окружность. Для ее нахождения на заданной окружности  x² + y² + 2x − 4y + 1 = 0,  выберем три точки, например: z₁ = −1 z₂ =  1 + 2i, z₃ = −3 + 2i, образами которых при отображении w  = 1/z будут точки

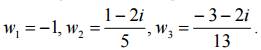
Точками w₁, w₂, w₃ однозначно определяется образ данной окружности, уравнение которой:

Для отображения w  = 1/z  имеем

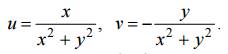
Выразив отсюда x = x(u, v), y = (u, v) и подставив в уравнение заданной окружности, получим искомый образ (3).

Пример 2.  Найти образ области D при отображении  ,   где   D = {z, 0 < Re(z) < 1, 0 < Im(z) < 1}.

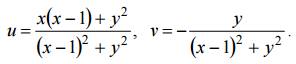
Будем искать образ границы области D (рис. 1).

Сторона  OA: y = 0, 0 ≤ x ≤ 1  отображается на отрицательную часть действительной оси (v = 0, − ∞ < u ≤ 0) (рис. 2).

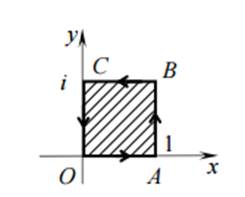
Рис. 1. Область D

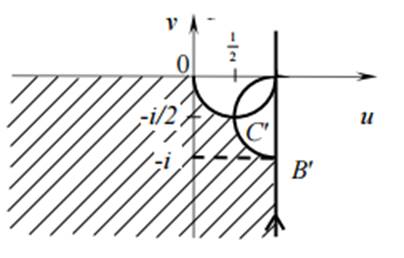
Рис. 2. Образ области D

Сторона  AB: x = 1, 0 < y ≤ 1, отображается в линию  u = 1, −∞ < v ≤ −1.

Сторона  BC: y =1, 1 ≥ x ≥ 0, отображается в линию, параметрическое уравнение которой имеет вид

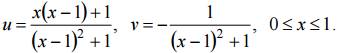
Исключив параметр x, получим

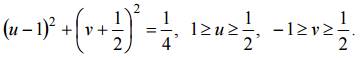
Аналогично образ стороны CO определяется уравнением

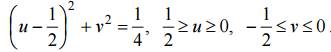
В соответствии с принципом соответствия границ образом квадрата будет заштрихованная область на рис. 1.

Пример 3. Найти дробно-линейное отображение, которое точки z₁ = 1 и z₂ = −1 оставляет неподвижными, а точку z₃ = i  переводит в точку  w₃ = 0.

Найти образ полуплоскости Im(z) > 0 при данном отображении.

Решение. По условию имеем три пары соответствующих точек

z₁ = 1,  z₂ = -1, z₃ = i,

w₁ = 1, w₂ = -1, w₃ = 0,

Применяя формулу (2), получим искомое дробно-линейное отображение.

Найдем теперь образ верхней полуплоскости, границей которой является действительная ось. Согласно круговому свойству действительная ось отображается в окружность. Чтобы найти ее, на действительной оси выберем три точки, например: z₁ =1, z₂ = 0, z₃ = −1, образами которых бу- дут точки  w₁ = 1, w₂ = −i, w₃ = −1. Они лежат на окружности |w| =1. По принципу соответствия границ получаем, что образом верхней полуплоскости будет область D'= {w, |w| < 1}.

Пример 4. Найти дробно-линейное отображение, которое круг  |z − 4i| < 2 отображает на полуплоскость v > u так, что w(4i) = −4, w(2i) = 0.

Решение. Условие задачи определяет две пары соответствующих точек. Третью пару найдем, пользуясь свойством симметрии дробно линейного отображения, согласно которому точки z₁ = 4i и z₃ = ∞, симметричные относительно окружности  |z − 4i| = 2, перейдут в точки w₁ = −4 и w₃ = − 4i, симметричные относительно прямой u = v . Таким образом, найдена третья пара точек z₃ = ∞ и w₃ = −4i. По формуле (2) найдем искомое отображение .

Скачано с www.znanio.ru