Конформные отображения. Логарифмы комплексных чисел. Степень с действительным показателем

Определение 3. Логарифмической функцией комплексного аргумента называется функция, обратная к показательной, т.е. определяемая уравнением

e^w = z, 0 z ≠ 0,

и обозначаемая w = Ln(z). Справедлива формула

Ln(z) = ln(|z|)+ i(arg(z) + 2kπ) k ∈ Z                               (7)

Логарифмическая функция определена на всей комплексной плоскости с выколотой точкой z = 0, она бесконечнозначна и разные ее значения отличаются на 2kπi k ∈ Ζ.

Каждое значение функции Ln(z) называется логарифмом комплексного числа z.

Значение логарифма комплексного числа z, z ≠ 0, которое соответствует ln(|z|) + i arg(z), называется главным значением Ln(z) и обозначается через ln(z):

ln(z) = ln(|z|) + i arg(z),  − π < arg(z) < π.

Тогда формула (7) принимает вид

Ln (z) = ln(z) + 2kπi,   k ∈ Z.

Определение 4. Однозначной непрерывной ветвью многозначной функции f (z) в области D называется однозначная непрерывная функция ϕ(z), значение которой в каждой точке z ∈ D совпадает с одним из значений функции f (z).

В области D, которая является комплексной плоскостью с разрезом вдоль луча, выходящего из начала координат под углом α₁ к действительной оси, существует бесчисленное множество разных однозначных ветвей функции w = Ln (z). Каждая из этих ветвей отображает область D на одну из полос:

Dk = {w, α₁ + 2kπ < Im(w) < α₁ + 2(k +1)π}, k ∈Z.

Для выделения однозначной ветви логарифмической функции w = Ln(z) достаточно определить полосу  D_k, на которую эта ветвь отображает область D. Для определения полосы  D_k  достаточно вычислить лишь значение логарифмической функции в какой-нибудь точке z₀ ∈ D.

Через Ln_k(z) обозначим ту ветвь логарифмической функции Ln(z), которая отображает область D на полосу D_k. Тогда

Ln_k(z) = Ln₀(z) + 2 kπi , k ∈ Z,

где Ln₀(z)  = ln(|z|) + iArg₀(z),  α₁ < Arg₀(z) < α₁ + 2π.

Очевидно, что каждая ветвь Ln_k(z)  удовлетворяет теореме о производной обратной функции, по которой

(Ln_k(z))'= 1/z,   k ∈ Z,   z ∈ D.

Отсюда, отображение, осуществляемое каждой ветвью логарифмической функции, является конформным для всех точек z ∈ D.

В связи с тем, что главное значение аргумента комплексного числа выбирается из промежутка [ −π,  π], в формуле (5) берут α₁ = −π. Тогда

Dk = {w, (2k −1)π < Im(w) < (2k +1)π}, k ∈ Z,

а область D будет плоскостью с разрезом по лучу [ −∞, 0].

Ветвь логарифмической функции, отображающая область D на полосу D₀, является главной ветвью ln(z). Все остальные однозначные непрерывные ветви функции w = Ln(z) в этой области имеют вид

Ln_k(z)= ln(z) + 2kπi, k ∈ Z.

Значение Ln(z), равное Ln_k(z), при однократном обходе точки z вокруг начала координат вдоль какой-нибудь окружности |z| = r переходит в число Ln_k+1(z), так, что Ln(z) непрерывно изменяется и обход совершается против движения часовой стрелки, и в число Ln_k−1(z)  – при обходе по часовой стрелке.

Точка, при обходе которой по какой-нибудь окружности достаточно малого радиуса многозначная функция, непрерывно изменяясь, переходит от одного значения к другому, называется точкой ветвления функции . Точки z = 0 и z = ∞ являются точками ветвления функции w = Ln(z).

Пример 7. Найти образы плоскости с разрезом вдоль отрицательной части действительной оси при отображениях ветвями логарифмической функции w = Ln(z) такими, что точка z₀ =1 переходит в точку w₀= 4πi.

Решение: полоса D_k, являющаяся образом плоскости с разрезом вдоль отрицательной части действительной оси, определяется ветвью Ln_k(z) логарифмической функции, которую найдем из условия  Ln_k(1) = 4πi.  Имеем:

Ln_k(z) = ln(|z|) + iarg(z) + 2kπi, k ∈ Z.

Положив в этом равенстве z = 1, получим 4πi = 2kπi т.е. k = 2. Отсюда условием Ln_k(1) = 4πi определяется ветвь Ln₂(z) = ln(z) + 4πi, которая согласно формуле (5) указанную область отображает на полосу:

D₂ = {w, 3π < Im(w) < 5π}.

Пример 8. Найти образ области D при отображении ветвью логарифмической функции w = Ln(z), которая определяется ее значением w0 в данной точке z₀ (при выборе ветви логарифмической функции комплексную плоскость разрезать по отрицательной части действительной оси)

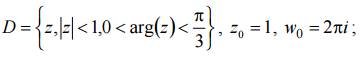
Решение: ветвь, определяемая условием Ln(1) = 2πi имеет вид

Ln₁(z) = ln(|z|) + i arg(z) + 2πi.

При этом отображении образом отрезка arg(z) = 0, 0 < |z| < 1, является луч v = 2π,  − ∞ < u < 0, а образом отрезка  arg(z) =  π/3, 0 < z < 1, является также луч  v = 7π/3, − ∞ < u < 0. Образом дуги окружности |z| =1, 0 < arg (z) < π/3, является отрезок u = 0, 2π < v < 7π/3. По принципу соответствия границ образом области D является полуполоса  − ∞ < u < 0, 2π < v < 7π/3.

Определение 5. Функция  w = zⁿ , n = 2,3, ... , называется целой степенной.

Она определена и однозначна на всей комплексной плоскости. Ее производная w' = nz^n-1 существует во всех точках плоскости, поэтому функция w = zⁿ аналитична во всей комплексной плоскости. Очевидно, производная  w' обращается в нуль лишь в точке  z = 0. Таким образом, отображение w = zⁿ конформно в каждой точке комплексной плоскости, кроме точки  z = 0. Положив  z = re^iϕ и w = ρe^iψ, найдем ρ = rⁿ, ψ = nϕ. Отсюда следует, что отображение w = zⁿ каждый вектор  z ≠ 0 поворачивает на угол (n −1) arg (z) и растягивает его в (n −1) раз. Это означает, что образом луча, выходящего из начала координат, является луч, также выходящий из начала координат; образом окружности |z| = R является окружность |z| = Rⁿ. Функция w = zⁿ отображает взаимно-однозначно и конформно внутренность любого угла с вершиной в точке  z = 0 и раствора α , 0 < α < 2π/n, на внутренность угла с вершиной в точке  w = 0 и раствора nα , 0 < nα < 2π. При α = 2π/n функция w = zⁿ отображает область D = {z, ϕ₀ < arg (z) < ϕ₀ + 2π/n} на плоскость с разрезом вдоль луча arg (w) = nϕ₀. Если ϕ₀ = 0, то область  D = {z, 0 < arg (z) < 2π/n} отображается на плоскость с разрезом вдоль положительной части действительной оси.

Функция w = , обратная к функции z = wⁿ, определена на всей комплексной плоскости, n-значна при  z ≠ 0.

За область D возьмем комплексную плоскость с разрезом по лучу, выходящему из начала координат под углом ϕ₀ к положительному направлению действительной оси. В этой области существует n различных ветвей

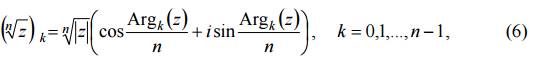
где 2πk + ϕ₀ < Argk(z) < ϕ₀ + π(k + 1), функции w = .

Каждая из ветвей взаимно-однозначно отображает область D на один из секторов

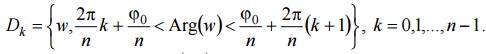
Для выделения ветви ()_k, k = 0, 1, ... , n − 1, достаточно определить сектор D_k, на который эта ветвь отображает область D. При проведении разрезов в комплексной плоскости чаще всего берут  ϕ₀ = 0 (разрез по положительному направлению оси Ox), либо ϕ₀ = −π (разрез по отрицательной части действительной оси).

В результате однократного обхода вокруг начала координат вдоль какой-либо окружности |z| = r значения , непрерывно изменяясь, переходят от ветви ()_k  к ветви ()_k+1 при обходе против часовой стрелки и к ветви ()_k−1  при обходе по часовой стрелке. После n-кратного обхода вокруг начала координат в одном направлении значение функции , переходя с одной ветви к другой, придет к исходному.

Точки z = 0 и z = ∞ являются точками ветвления функции  w = .

Каждая ветвь функции n w = z удовлетворяет теореме о производной обратной функции, по которой

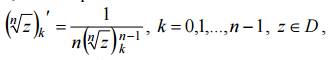
и поэтому осуществляет конформное отображение области D на одну из областей D_k.

Пример 9.В указанной области выделить однозначную ветвь заданной многозначной функции и найти, если необходимо, ее значение в точке:  в плоскости z с разрезом по положительной части действительной оси найти значение ветви функции  в точке z = 8i при условии  = −1.

Решение: по формуле (6)

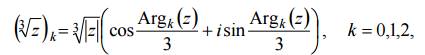
где 2πk < Arg_k(z) < 2π(k +1), так как  ϕ₀ = 0. Из условия  = −1 имеем

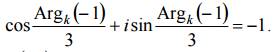
Отсюда

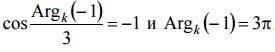
Таким образом, k = 1  и искомая ветвь имеет вид

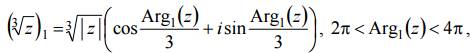
а ее значением в точке z = 8i будет

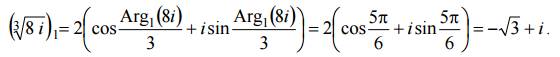
Определение 6. Степенной функцией комплексного аргумента z, z ≠ 0 , с показателем α , α ∈ C, называется функция, определяемая равенством z^α = e^αLn(z).

Если α не является рациональным числом, то функция z^α бесконечнозначна. Точки z = 0 и z = ∞ являются ее точками ветвления.

Пусть z = re^iϕ. Тогда

и

Беря все возможные значения k , получим все ветви этой функции в области D = {z, z ∈ [ −∞; 0]}. Производная каждой ветви функции z^α определяется по формуле

и существует во всех точках области D . Это означает, что каждая ветвь функции z^α аналитична во всех точках области D .

Определение 7. Показательная функция определяется равенством

Рассматривая все возможные значения Ln(a) получим все ветви функции z^α. Чтобы получить отдельную ветвь, достаточно фиксировать одно из значений Ln(a). Многозначная функция z^α не имеет точек разветвления и ее ветви не могут непрерывно переходить одна в другую. Все ветви показательной функции являются аналитичными на всей комплексной плоскости, и имеет место формула

Скачано с www.znanio.ru