Конформные отображения, определяемые комбинациями основных элементарных функций

Конформные отображения, определяемые комбинациями основных элементарных функций

Основные задачи теории конформных отображений имеют следующий вид: даны области D и G , требуется найти функцию f (z), осуществляющую конформное отображение области D на область G .

Один из методов поиска функции f(z), если такую функцию можно найти, основан на подборе надлежащим образом элементарных функций, рассмотренных ранее.

Пример 10. Найти конформное отображение области D на область G, если:

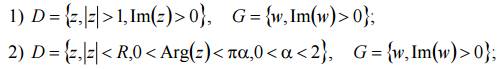
Решение: 1) область D ограничена полуокружностью |z| = 1, Im(z) > 0 и лучами  [−∞; −1] и [1 ;+∞] которые пересекаются с полуокружностью в точках  z = ± 1под прямым углом (рис 5, а). Дробно-линейная функция

точку z = −1 переводит в точку w₁ = ∞ , а точку z =1 – в точку w₁ = 0.

Пользуясь свойством сохранения углов при конформном отображении, получим, что область D отображением (13) переводится на внутренность прямого угла с вершиной в точке  w = 0. Одна из сторон этого угла – положительная часть мнимой оси (образ полуокружности), другая – положительная часть действительной оси (образы лучей [ −∞; −1] и [1 ;+∞]) (рис 5, б). Функция w = (w₁)²  переводит квадрант на верхнюю полуплоскость, т.е. функция

осуществляет отображение области D на верхнюю полуплоскость (рис. 5, в);

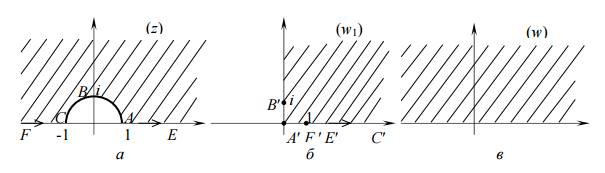
Рис. 5

2) с помощью степенной функции w₁ = z^1/α данный сектор (рис. 6, а) переводится на верхний полукруг радиуса R^1/α  (рис. 6, б). Легко видеть, что дробно-линейная функция

внутренность полукруга |w₁| < R^1/α, Im(w₁) > 0 (рис. 6, б), отображает на первый квадрант плоскости w₂ (рис. 6, в).

Отображением w = (w₂)² этот квадрант переводится на верхнюю полуплоскость (рис. 6, г).

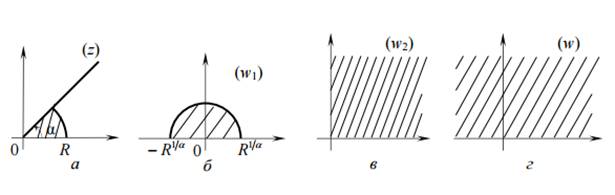
Рис. 6

Итак, искомое отображение имеет вид

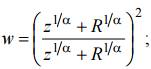
3) область D является внутренностью угла с разрезом по лучу [e^iα; +∞ e^iα] (рис. 8, а). Отображение w₁ = z^π/α  переводит область D на всю комплексную плоскость с разрезом по лучам [ − ∞,−1] и [0  ,+∞] (рис. 7, б), а отображение

переводит эту область на верхнюю полуплоскость (рис 7, в). Тогда отображение w = 1/π ln (w₂) переводит верхнюю полуплоскость плоскости W₂ на полосу 0 < Im(w) < 1 (рис 8, г). То есть функция

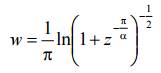
осуществляет искомое отображение (рис. 7, а и г).

Рис. 7