Конспект лекций по дисциплине ЕН.03 Химия (раздел Физколлоидная химия)

Мичуринский государственный аграрный университет»

Содержание

Зависимость скорости реакции от температуры……………………………… 26

Лекция 12. Микрогетерогенные системы ……………………………………

Лекция 1 ОСНОВЫ ХИМИЧЕСКОЙ

Процесс, который можно провести в прямом и обратном направлении без изменения не только в системе, но в окружающей среде, называется обратимым

Работа – это форма передачи энергии путем упорядочного направленного движения частиц

Термохимия. Теплота реакции (тепловой эффект)

Следствия из закона Гесса 1

N N å n i × C p ( кон ) - å n j ×

Рассчитайте (в Дж) разность тепловых эффектов реакции

Энтропия является мерой направленности процессов в изолированной системе или для адиабатических процессов d

Термодинамические функции Задачей

Химическ и й потенциал и общие услови я р а в новеси я систем

В результате расширения 20 кг гелия при температуре 298

Моляльная концентрация (С т ) , моль/1000 г раст-ля – число моль растворенного вещества в 1000 г растворителя:

Р 1 =Р 1 º Х 1 и

D Т кип = Т кип ( р - ра ) -

Рассмотрим системы с ограниченной растворимостью двух жидкостей

Рассчитайте осмотическое давление 0,01

C d C c K C

Термодинамическая теория химического сродства

R > 0, T равновесие реакции

Вопросы для самоконтроля 1

A = - 1 dc

Таблица 5.1. Формальная кинетика реакций различных порядков порядок константа скорости k , время t период реакции размерность полупревращения t 1/2 нулевой k = c

T+10 и k T – константы скорости реакции соответственно при температурах

Что такое порядок и молекулярность реакции?

К дис = [ А [ + ] × [ В ] - ]

Na 3 PO 4 + NaH 2 PO 4 . Меняя концентрацию и соотношение растворов можно получить буферные растворы с различным значением рН

R – сопротивление электролита,

Скорость движения ионов. Числа переноса

Адсорбция относится к поверхностным явлениям

Адсорбция на твердой поверхности из растворов

Существуют также амфотерные адсорбенты, которые в одних условиях обменивают катионы, а в других – анионы

Обобщенная теория С.Брунауэра,

Поверхностное натяжение – это сила (

R), чем длиннее неполярный радикал, тем легче молекулы

Адгезия и когезия Эти поверхностные явления часто сопровождают друг друга

А А > А К : адгезия (сила притяжения жидкость/твердая поверхность) больше чем когезия (силы притяжения молекул жидкости), то капля жидкости растекается по твердой поверхности,…

Лекция 9 ДИСПЕРСНЫЕ СИСТЕМЫ 9

Таблица 9.1. Классификация дисперсных систем по степени дисперсности частиц дисперсной фазы

В качестве примера таких систем можно привести коллоидные растворы

Суть метода: к свежеприготовленному рыхлому осадку прибавляют электролит (пептизатор), благодаря которому частицы осадка отделяются друг от друга и переходят в раствор

Ультрафильтрация основана на отделении дисперсной фазы от дисперсионной среды путем фильтрования коллоидных растворов через особые плотные пленки – ультрафильтры, способные задерживать коллоидные частицы

Лекция 10 СВОЙСТВА ДИСПЕРСНЫХ

Электроосмос Эл е ктро о см осо м на зы ва ют пер емещ е ние дисперсионной среды под де й с т в и…

Интенсивность рассеянного света пропорциональна частичной концентрации золя

Лекция 11 УСТОЙЧИВОСТЬ ДИСПЕРСНЫХ

Адсорбционно-сольватный фактор – уменьшение межфазного натяжения при взаимодействии частиц дисперсной фазы со средой (благодаря адсорбции и сольватации);

федеральное государственное бюджетное образовательное учреждение

высшего образования

«Мичуринский государственный аграрный университет»

Центр-колледж прикладных квалификаций

КОНСПЕКТЫ ЛЕКЦИЙ

дисциплины

ЕН. 03 ХИМИЯ (раздел ФКХ)

программы подготовки специалистов среднего звена (ППССЗ)

по специальности 19.02.05 Технология бродильных производств и виноделие

Базовая подготовка

Преподаватель: Филиппова Татьяна Ивановна

Рассмотрены на заседании ЦМК технических специальностей

Протокол №1 от «31» августа 2023 г

Председатель ЦМК___________/В.В.Кусова/

Мичуринск- 2023

	Содержание

Лекция 1. Основы химической термодинамики………………………………...		5
1.1. Основные понятия химической термодинамики…………………………….		5
1.2. Первое начало термодинамики…………………………………….………….		6
1.3.	Понятия внутренней энергии, работы, теплоты и теплоемкости
термодинамической системы……………………………………………………….		6
1.4. Расчет работы, теплоты и изменения внутренней энергии ………………...		7
1.5. Термохимия. Теплота реакции (тепловой эффект) …………………….…….		8
1.6. Закон Гесса………………………………………………………………….......		8
1.7. Следствия из закона Гесса……………………………………………………..		9
1.8. Зависимость теплового эффекта от температуры. Закон Кирхгофа….…….		9
Вопросы для самоконтроля…………………………..……………………………...		10

Лекция 2. Второе и третье начало термодинамики. Термодинамические
функции………………………………………………………………………………...		11
2.1. Второе начало термодинамики…………….………………………………….		11
2.2.	Свойства энтропии…...…………………………………………………………	11
2.3. Статистическое толкование энтропии и II начала термодинамики.…………		12
2.4. Третье начало термодинамики (постулат Планка)……………………………		12
2.5. Расчет изменения энтропии при различных процессах………………………		12
2.6.Термодинамические функции………...…………………………………………		13
2.7. Свободная энергия Гиббса и Гельмгольца …………………………………....		13
2.8. Химический потенциал и общие условия равновесия систем………….…...		14
Вопросы для самоконтроля……..…………………………………………………...		14

Лекция 3. Термодинамические свойства растворов. ……………………………		15
3.1. Общая характеристика растворов…………..…………………………………		15
3.2. Термодинамические условия образования идеальных растворов…………..		16
3.3. Закон Рауля………...……………………………………………………………		16
3.4. Понижение температуры замерзания растворов………..……………………		17
3.5. Повышение температуры кипения растворов…….…………………………..		17
3.6. Осмос и осмотическое давление……………………………………………….		18
3.7.	Ограниченная взаимная растворимость жидкостей…….……………………	18
Вопросы для самоконтроля……………………………………………….………....		19

Лекция 4. Химическое равновесие…………………………………...……………..		20
4.1. Закон действующих масс. Признаки химического равновесия………………		20
4.2. Способы выражения константы равновесия…………………………………..		20
4.3. Уравнение изотермы химической реакции……...…………………………….		21
4.4. Термодинамическая теория химического сродства………...…………………		22
4.5. Смещение химического равновесия……………………………………………		22
Вопросы для самоконтроля………….……………………………………………....		23

Лекция 5. Химическая кинетика …………………………...………………………		24
5.1. Скорость химической реакции……………..………………………………….		24
5.2. Зависимость скорости реакции от концентрации. Порядок и
молекулярность реакции……...……………………………………………………..		25

5.3. Формальная кинетика реакций различных порядков…………………………	25
5.4. Зависимость скорости реакции от температуры………………………………	26
Вопросы для самоконтроля……….………………………………………………....	27

Лекция 6. Электрохимия……………………………………………………………..	28
6.1. Растворы электролитов………………………………………………………….	28
6.2. Диссоциация воды. Ионное произведение воды. Понятия рН и рОН………	29
6.3. Буферные растворы…..…………………………………………………………	29
6.4. Электропроводность растворов электролитов ………………………………..	30
Вопросы для самоконтроля……….………………………………………………....	31

Лекция 7. Термодинамика поверхностных явлений……………………………..	32
7.1. Понятия поверхностных явлений………………………………………………	32
7.2. Адсорбция. Основные понятия. Классификация…………………………….	32
7.3. Адсорбция из газов на твердом адсорбенте……….…………………………..	33
7.4. Адсорбция на твердой поверхности из растворов…...………………………..	34
7.5. Адсорбция электролитов……………………………………………………….	34
7.6. Обменная адсорбция……………………………………………………………	34
7.7. Теории адсорбции……………………………………………………………….	35
Вопросы для самоконтроля………………………………………………………....	36

Лекция 8. Поверхностное натяжение. Адгезия, смачивание и растекание …..	36
8.1. Понятие поверхностного натяжения…………………………………………..	36
8.2. Поверхностно-активные вещества (ПАВ)……………………………………..	37
8.3. Полуколлоиды…………………………………………………………………..	38
8.4. Адгезия и когезия…………………………………………………………….....	39
8.5. Явление растекания……………………………………………………………..	39
8.6. Явление смачивания…………………………………………………………….	39
Вопросы для самоконтроля………………………………………………………....	40

Лекция 9. Дисперсные системы………………………………………………..……	41
9.1. Дисперсные системы, их классификация……...………………………………	41
9.2. Получения дисперсных систем…………………………………………………	43
9.3. Строение мицелл………………...………………………………………………	44
9.4. Методы очистки дисперсных систем…………………………………………..	44
Вопросы для самоконтроля………………………………………………………....	45

Лекция 10. Свойства дисперсных систем………………………………………….	45
10.1. Механизмы образования и строения двойного электрического слоя
(ДЭС)........................................................................................................................	45
10.2. Электрокинетические явления дисперсных систем………..………………..	46
10.3. Оптические свойства дисперсных систем……………………………………	46
Вопросы для самоконтроля………………………………………………………....	48

Лекция 11. Устойчивость дисперсных систем……………………………………	48
11.1. Седиментация в дисперсных системах……………………………………….	48
11.2. Термодинамические и кинетические факторы агрегативной устойчивости	49
11.3. Коагуляция коллоидных растворов……….…………………………………	49

11.4. Механизмы электролитной коагуляции……………………………………… 50

11.5. Коллоидная защита……………………..…………………………………….. 51

Вопросы для самоконтроля……………………………………………………….... 51

Лекция 12. Микрогетерогенные системы……………………………………..…... 52

12.1. Золи и суспензии………………………………………………………………. 52

12.2. Эмульсии……..………………………………………………………………… 52

12.3. Пены…….. ……………………………………………………………………............ 54

12.4 Аэрозоли……….. ……………………………………………………………….......... 55

Вопросы для самоконтроля……………………………………………………….... 55

Лекция 13. Растворы высокомолекулярных соединений (ВМС)……………… 56

13.1. Определение, классификация ВМС…………..……………………………… 56

13.2. Особенности растворов ВМС……………….……………………………….. 57

13.3. Электрические свойства растворов ВМС…………..……………………….. 57

13.4. Молекулярно-кинетические свойства растворов ВМС…………………….. 58

13.5. Оптические свойства растворов ВМС……………………………………….. 58

13.6. Растворение ВМС. Набухание…………….. ………………………………….......... 58

13.7. Вязкость растворов ВМС……..………………………………………………. 59

Вопросы для самоконтроля……………………………………………………….... 61

Лекция 14. Студнеобразования в коллоидных растворах. Гели и студни…… 61

14.1. Процессы структурообразования в коллоидных системах…………………. 61

14.2. Гели и студни. Определение. Классификация………………………………. 62

14.3. Строение гелей и студней………..…………………………………………… 63

14.4. Методы получения гелей………... …………………………………………….......... 63

14.5. Свойства студней………………...……………………………………………. 64

Вопросы для самоконтроля……………………………………………………….... 64

Лекция 1

ОСНОВЫ ХИМИЧЕСКОЙ ТЕРМОДИНАМИКИ

1.1. Основные понятия химической термодинамики

Химическая термодинамика – область физической химии, в которой на основе законов общей термодинамики изучаются тепловые балансы физических и химических процессов в различных условиях, устанавливается возможность и направление течения процесса.

Термодинамическая система – это тело или группа тел, находящихся во взаимодействии и отделенные видимой или воображаемой поверхностью раздела от окружающей среды. Окружающая среда – это все тела вне системы.

Термодинамические системы состоят из очень большого числа малых частиц, т. е.

является макросистемой. Различают следующие термодинамические системы:

1. Открытая (есть обмен с окружающей средой и энергией, и веществом). Пример: живой организм.

2. Закрытая (есть обмен с окружающей средой только энергией). Пример: запаянная ампула.

3. Изолированная (нет обмена с окружающей средой ни веществом, ни энергией). Примером системы, приближающейся к изолированной, является закрытый сосуд Дьюара (термос), заполненный смесью воды со льдом.

Система характеризуется некоторыми физическими и химическими свойствами: давлением (Р), объемом (V), температурой (Т), концентрацией (С) и т. д. Эти свойства называются параметрами системы. Параметры классифицируются на:

· Независимые (могут изменяться в некоторых пределах).

· Зависимые (принимают единственно возможное значение в данных условиях). Параметры бывают:

· Интенсивные (не зависят от массы вещества и не подчиняются закону аддитивности). Пример: давление Р, температура Т.

· Экстенсивные (зависят от массы вещества и подчиняются закону аддитивности). Пример: объем V, концентрация C.

Совокупность параметров, принимающих определенное значение, определяют состояние системы. Параметры связаны между собой уравнением, которое называется уравнением состояния: f (p, V, T) = 0. Например, для идеального газа это уравнение Менделеева-Клапейрона: PV = nRT.

Под термодинамическим процессом понимают всякое изменение состояния системы, сопровождающееся изменением хотя бы одного параметра состояния.

Термодинамический процесс классифицируются на: · Изотермический (T = const).

· Изобарный (Р = const).

· Изохорный (V = const).

· Адиабатический (нет обмена теплотой между системой и внешней средой, Q=0). Термодинамические процессы также бывают:

· Обратимые и необратимые.

· Равновесные и неравновесные.

Равновесный процесс – это непрерывный бесконечно медленный ряд равновесных состояний, через которые проходит система в прямом и обратном направлении и при этом совершается максимальная работа.

Процесс, который можно провести в прямом и обратном направлении без изменения не только в системе, но в окружающей среде, называется обратимым.

Сравнивая понятия равновесный и обратимый процесс, можно видеть, что эти понятия отражают один и тот же процесс.

Если же в результате протекания процесса в прямом и обратном направлениях в системе останутся какие-либо изменения, то процесс называется необратимым. Необратимость не означает, что его нельзя провести в обратном направлении. Необратимый означает лишь то, что это возращение невозможно при помощи той же работы и теплоты, которые были получены при прямом процессе.

1.2. Первый закон термодинамики

Первый закон термодинамики является законом сохранения и превращения энергии применительно к термодинамическим процессам. Первый закон термодинамики имеет несколько формулировок, но все они выражают одну и ту же суть: сохранение и эквивалентность энергии при взаимных переходах различных видов ее друг в друга.

Формулировки I закона термодинамики:

· Энергия не возникает из ничего и не исчезает бесследно, а переходит из одной формы в другую в строго эквивалентном соотношении.

· В изолированной системе сумма всех видов энергии постоянна.

· Вечный двигатель (перпетум мобиле) первого рода невозможен, т. е. машины, которая совершала бы работу, не затрачивая на это соответствующего количества энергии из вне.

Аналитическое выражение I закона термодинамики для закрытой системы:

dU = δQ – δA (дифференциальная форма)

U = Q – A (интегральная форма);

для изолированной системы:

dU = 0 (дифференциальная форма)

U = 0 (интегральная форма).

Из первого закона термодинамики следует: для всех термодинамических систем существует функция состояния, называемая внутренней энергией (U), изменение которой при переходе системы из состояния 1 в состояния 2 равно разности между теплотой (Q), поглощенной системой из окружающей среды, и работой (A), совершенной системой. Функциями состояния называются такие функции, которые не зависят от пути перехода, а определяются только начальным и конечным состояниями.

1.3. Понятия внутренней энергии, работы,

теплоты и теплоемкости термодинамической системы

Полная энергия термодинамической системы складывается из кинетической и потенциальной энергии системы в целом (Екин + Епот) и внутренней энергии (U).

Внутренняя энергия – это энергия ядер, электронов, энергия связей атомов в молекуле, энергия взаимодействия между молекулами, вращательная, поступательная, колебательная энергия частиц и т. д.

Внутренняя энергия – это совокупность потенциальной и кинетической энергий частиц, составляющих систему. Для нее нет нуля отсчета, т. е. нет такого состояния, где U = 0.

Изменение внутренней энергии, как следует из первого закона термодинамики, возможно за счет совершения работы и передачи тепла, поэтому:

Работа – это форма передачи энергии путем упорядочного направленного движения частиц.

Теплота – это форма передачи энергии путем неупорядочного хаотического движения частиц.

Теплота и работа не обладают свойствами функции состояния, так как зависят от пути перехода из состояния 1 в состояние 2. Нельзя говорить, что система обладает запасом энергии и тепла, т.к. эти величины зависят от условий перехода, т. е. являются функциями процесса.

В Международной системе единиц (СИ) внутренняя энергия, теплота и работа имеют размерность энергии и выражаются в джоулях (Дж).

Важнейшим свойством теплоты является теплоемкость.

Теплоемкость – это количество тепла, которое нужно подвести к единице вещества, чтобы повысить его температуру на 1 градус. Если единицей вещества является 1 г, то это удельная теплоемкость (Суд), если – 1 моль, то это молярная теплоемкость (С).

Суд, [Дж/(г·К)]; С, [Дж/(моль·К)]; С = Суд·М, М – молярная масса вещества. Различают среднюю и истинную теплоемкости.

Средняя теплоемкость:

C = ^Q .

T₂ - T₁

Истинная теплоемкость соответствует бесконечно малому изменению температуры:

С = ^¶_¶^Q_T .

В зависимости от условий, при которых производят нагревание, различают теплоемкости при постоянном объеме СV и при постоянном давлении Ср.

C_V = ^dU_dT ;C_p = ^dH_dT .

Функция Н = U + pV называется энтальпия. Так как U, p, V – функции состояния, то

и Н является функцией состояния. Теплоемкость не является функцией состояния, так как зависит от типа процесса.

Изобарная теплоемкость связана с изохорной теплоемкостью формулой Майера:

C p = CV + R.

1.4. Расчет работы, теплоты и изменения внутренней энергии

Выражения для зависимости теплоты, работы и изменения внутренней от параметров p, V, T системы в конечном и начальном состоянии системы в основных процессах с идеальным газом приведены в таблице.

	Изменение	Работа	Теплота
Процесс	внутренней	Работа	Теплота
Процесс	внутренней	(А)	(Q)
	энергии (ΔU)	(А)	(Q)
	энергии (ΔU)

Изотермический	U = 0	nRTln(V2/V1)	А = Q
(Т = const)	U = 0	nRTln(p1/p2)	А = Q
(Т = const)		nRTln(p1/p2)

Изобарный	U = А + Q	p(V2 - V1)	nCp(T2 – T1)
(p = const)	U = А + Q	nR(T2 – T1)	nCp(T2 – T1)
(p = const)		nR(T2 – T1)

Изохорный	U = Q	0	nCV(T2 – T1)
(V = const)	U = Q	0	nCV(T2 – T1)
(V = const)

1.5. Термохимия. Теплота реакции (тепловой эффект)

Термохимия – раздел химической термодинамики, изучающий тепловые процессы, сопровождающие химические реакции и фазовые превращения.

Тепловой эффект реакции – эта та теплота, которая выделяется или поглощается в ходе полностью необратимого изобарного (когда совершается только работа расширения) или изохорного (когда никакой работы не совершается) процессов при условии, что температура исходных и конечных веществ одинакова.

Тепловой эффект реакции при постоянном объеме (Qv) соответствует изменению внутренней энергии между конечном и начальном состояниями:

Qv = U = U2 – U1

Теплота реакции при постоянном давлении равна изменению энтальпии:

Q_p = DH = H₂ - H₁.

Если Qp, QV < 0, то реакция эндотермическая (система поглощает теплоту).

Если Qp, QV > 0, то реакция экзотермическая (система выделяет теплоту).

Н > 0 – реакция эндотермическая; Н < 0 – реакция экзотермическая.

Термодинамическая форма записи: Сграф + О2(г) = СО2(г); Н = - 393,5 кДж.

Термохимическая форма записи: Сграф + О2(г) = СО2(г) + 393,5 кДж.

Между Qp и QV для реакции с участием идеальных газов существует соотношение. Рассмотрим реакцию аА + bB → cC + dD. Если реакция идет при постоянном

давлении р и если V2 и V1 – соответственно объемы конечного и начального состояний, то

DH = DU + pDV = DU + p(V2 -V1 ); DH = Qp ; DU = QV Þ Qp = QV + pDV Так как реакция осуществляется между идеальными газами, то

pV2 = (c + d )RT ; pV1 = (a + b)RT

откуда Qp = QV + [(c + d )- (a + b)]RT = QV + DnRT , где Δn – изменение числа молей газообразных конечных и исходных веществ реакции.

Для жидких и твердых веществ: DV = 0 Þ Qp » QV .

1.6. Закон Гесса

Основой термохимии является закон Гесса (1840 г.): Если из одних и тех же исходных веществ можно получить одни и те же конечные вещества, но разными путями, то суммарный тепловой эффект по одному пути будет равен суммарному тепловому эффекту по другому пути.

Закон Гесса обязателен только для процессов, протекающих при постоянном объеме или давлении. Аналитическое выражение закона Гесса:

N	N
DHх. р. = ån i × DH f ,298(кон) - ån j × DH f ,298(исх)
i=1	j =1

где DH _f _,298 - стандартная теплота образования вещества; n_i ,n _j - стехиометрические

коэффициенты. Таким образом, тепловой эффект реакции равен разности сумм стандартных теплот образования конечных и исходных веществ.

Стандартной теплотой образования вещества называется теплота, выделяемая или поглощаемая при образовании 1 моль вещества из простых веществ или элементов при стандартных условиях (t = 25 ºC, р = 1 атм). Теплоты образования простых веществ равны нулю. Значения стандартных теплот образования находятся в справочниках.

1.7. Следствия из закона Гесса

1. Тепловой эффект прямой реакции равен по величине и противоположен по знаку тепловому эффекту обратной реакции. Например:

½ Н2 + ½ Cl2 = HCl, DHх. р. = -92,3кДж/ моль

HCl = ½ Н2 + ½ Cl2, DHх. р. = 92,3кДж/ моль

2. Если совершаются две реакции, приводящие из различных исходных состояний

к одинаковым конечным состояниям, то разница между их тепловыми эффектами представляет собой тепловой эффект перехода из одного начального состояния в другое.

3. Если совершаются две реакции, приводящие из одинаковых исходных состояний

к различным конечным состояниям, то разница между их тепловыми эффектами представляет собой тепловой эффект перехода из одного конечного состояния в другое.

4. Тепловой эффект реакции равен разности между суммой теплот сгорания исходных веществ и суммой теплот сгорания конечных веществ.

DHх. р. = ån i × DHсгор(исх) - ån j × DHсгор(кон)

i=1

где n_i ,n _j - стехиометрические коэффициенты; DH_сгор - стандартные теплоты сгорания.

Стандартной теплотой сгорания вещества – называется тепловой эффект окисления кислородом 1 моль вещества с образованием высших оксидов и воды при стандартных условиях. Теплоты сгорания высших оксидов принимают равными нулю.

1.8. Зависимость теплового эффекта от температуры. Закон Кирхгофа

Вторым законом термохимии является зависимость теплового эффекта от температуры.

æ	¶Q_p ö		æ ¶DH ö
ç		÷	= ç		÷

ç	¶T	÷		¶T
è		ø_p	è		ø_p

закон

= DC_p

Кирхгофа, показывающий

N	N
åni ×C p(кон) - ån j ×C p(исх) = DС p
i-1	j =1

Это уравнение представляет собой дифференциальную форму закона Кирхгофа, из которого следует, что изменение теплового эффекта от температуры определяется изменением теплоемкости в ходе процесса.

Проанализируем уравнения Кирхгофа.

	æ	¶DH ö
1). DC_p	= 0 Þ ç		÷	= 0	Þ DH - не зависит от температуры.

	è	¶T ø_p
	æ	¶DH ö
2). DC_p	> 0 Þ ç		÷	> 0	Þ DH увеличивается с увеличением температуры.

	è	¶T ø_p
	æ	¶DH ö
3). DC_p	< 0 Þ ç		÷	< 0 Þ DH уменьшается с увеличением температуры.

	è	¶T ø_p

Для определения абсолютного значения теплового эффекта процесса при температуре Т используют интегральную форму закона Кирхгофа ( DC_p = const ):

DH_T = DH₂₉₈ + DC_p (T - 298)

Возможность определения теплового эффекта химической реакции при заданной температуре только расчетным путем имеет большое значение. Экспериментальное определение тепловых эффектов при повышенных температурах часто сопряжено с большими трудностями, чем измерение в тех же условиях теплоемкостей.

Вопросы для самоконтроля

1. Определение понятия «термодинамическая система». Типы термодинамических систем. Примеры.

2. Параметры состояния зависимые и независимые, интенсивные и экстенсивные.

3. Типы термодинамических процессов (обратимые, необратимые, самопроизвольные, несамопроизвольные).

4. Понятие, примеры и свойства функций состояния и функций процесса.

5. Формулировки первого начала термодинамики. Математическое выражение первого закона термодинамики для бесконечно малого и конечного изменения состояния для закрытой

и изолированной систем.

6. Внутренняя энергия системы. Теплота и работа как формы передачи внутренней энергии.

7. Понятие теплоемкости и какие факторы влияют на ее величину. Каково соотношение между изобарной и изохорной теплоемкостями для идеального газа.

8. Приведите определение понятия тепловой эффект процесса.

9. Тепловые эффекты реакции при постоянном объеме и давлении и связь между ними.

10. Сформулируйте закон Гесса и следствия из него.

11. Что называется стандартной теплотой образования и сгорания?

12. Какие факторы влияют на величину теплового эффекта? Приведите выражения закона Кирхгофа в дифференциальной и интегральной форме.

13. Чему равна работа, совершаемая при изотермическом расширении 3,5 кг азота, от 20 м³ до 60 м³ при температуре 298 К? (Ответ: 358 кДж).

14. Найдите теплоту, работу и изменение внутренней энергии при изобарическом нагревании 2 кмоль СО2 от 300 К до 550 К. Изобарная теплоемкость СО2 равна 37,11

Дж/(моль^žК). (Ответ: Q = 18555 кДж, A = 4157 кДж, ΔU = 14398 кДж).

15. Какой знак имеет изменение энтальпии в следующих процессах: а) сгорания водорода, конденсация водяного пара, испарение ацетона, разложение молекулярного водорода на атомарный?

16. Рассчитайте (в Дж) разность тепловых эффектов реакции СН3СНО(г) + Н2(г) = С2Н5ОН(ж), протекающей при температуре 298 К при постоянном давлении и постоянном объеме. (Ответ:

Qp – QV = - 4955 Дж).

17. Определить тепловой эффект реакции этерификации щавелевой кислоты метиловым спиртом, протекающей по уравнению:

(СООН)2(кр) + 2СН3ОН(ж) ⇄ (СООСН3)2(ж) + 2Н2О(ж),

если мольные теплоты сгорания при р = const: DН^°сг (СООН)2(кр) = -251,46 кДж/моль; DН^°сг

СН3ОН(ж) = -726,55 кДж/моль; DН^°сг (СООСН3)2(ж) = -167,78 кДж/моль. (Ответ: -1536,78 кДж).

18. Определить тепловой эффект реакции образования бензола из ацетилена по уравнению 3С2Н2 = С6Н6 при 348 К, зная, что при 290 К тепловой эффект равен -547,27 кДж/моль, а средние мольные изобарные теплоемкости ацетилена и бензола в этом интервале температур

соответственно равны Ср(ац) = 43,64 Дж/К×моль, Ср(бенз) = 133,89 Дж/К×моль. (Ответ: -547,1 кДж).

19. Рассчитайте тепловой эффект (ΔНºх.р.) следующей химической реакции:

2CI2 + 2Н2О(г) = 4НCI + О2,

если стандартные теплоты образования: Нºобр(Н2О(г)) = -241,81 кДж/моль, Нºобр(НCl) = -

92,31 кДж/моль (Ответ: 114,38 кДж).

Лекция 2

ВТОРОЕ И ТРЕТЬЕ НАЧАЛО ТЕРМОДИНАМИКИ.

ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ

2.1. Второе начало термодинамики

Самопроизвольным (положительным) называется процесс, который может проходить сам собой без соединения его с другим. В результате протекания такого процесса получают работу.

Несамопроизвольным (отрицательным) называется процесс, которой сам собой не идет. Чтобы заставить идти отрицательный процесс, необходимо соединить (компенсировать) его положительным процессом.

Существуют многочисленные формулировки второго закона, которые как можно показать, эквивалентны друг другу. Приведем некоторые из них.

1. Единственным результатом любой совокупности процессов не может быть отрицательный процесс.

2. Единственным результатом любой совокупности процессов не может быть переход теплоты от холодного тела к горячему (Клаузиус).

3. Теплота наиболее холодного из участвующих в процессе тел не может быть источником работы (Томсон).

4. Невозможно построить такую машину (вечный двигатель второго рода), работающую циклами, работа, которой производилась ба только за счет охлаждения теплового источника без каких-либо изменений в других телах (Планк).

Аналитическое выражение II закона термодинамики: dS ³ ^d_T^Q

Знак равенства – для равновесных обратимых процессов, а неравенство – для необратимых (самопроизвольных) процессов. Функцию S Клаузиус назвал энтропией.

2.2. Свойства энтропии

1. Энтропия является функцией состояния.

2. Энтропия является мерой хаоса в системе. Чем больше хаос, тем энтропия

больше: Sтв. сост. < Sжид. сост. < Sреал. газ < Sидеал. газ.

3. Энтропия является мерой направленности процессов в изолированной системе или для адиабатических процессов dQ = 0 Þ dS ³ 0. Следовательно,

· для самопроизвольных процессов: dS > 0;

· для равновесных процессов: dS = 0;

· для несамопроизвольных процессов: dS < 0.

2.3. Статистическое толкование энтропии и II закона термодинамики

Увеличение энтропии всегда сопровождается ростом хаотического молекулярного состояния системы. Более хаотичное состояние может осуществляться большим числом способов. Его можно считать более вероятным. Параметры состояния системы определяют макросостояние системы, а положение частиц системы в данный момент

времени – это микросостояние. Число микросостояний соответствующих макросостоянию называется термодинамической вероятностью (W), т. е. число микросостояний, которым может быть достигнуто макросостояние.

По уравнению Больцмана: S = ^RlnW = kБ lnW ,

N A

где kБ = 1,88·10^-23 Дж/К – постоянная Больцмана.

Таким образом, энтропия является статистической функцией, и все термодинамические функции, связанные с энтропией, являются статистическими, т. е. показывают наиболее вероятное состояние или более вероятный переход.

2.4. Третий закон термодинамики (постулат Планка)

В 1906 г. Нернст пришел к выводу, что изменение энтропии многих химических реакций вблизи абсолютного нуля (0 К) пренебрежимо мало: dS_T ₌₀ = 0 .

В 1912 г. Планк высказал экспериментально недоказуемое утверждение (постулат). Постулат Планка называют третьем законом термодинамики, который формулируется следующим образом: Энтропия идеально построенного кристалла индивидуального вещества при абсолютном нуле равняется нулю.

^ST =0⁼ ⁰

Из уравнения Больцмана S = k_Б lnW видно, S = 0 при условии, когда термодинамическая вероятность равна 1 (W = 1), т.е. такое состояние только одно.

Постулат Планка позволяет рассчитать абсолютное значение энтропии вещества в любом агрегатном состоянии, так как устанавливает начало отсчета энтропии:

DS = S_T - S_T ₌₀ = S_T - абсолютное значение энтропии

2.5. Расчет изменения энтропии при различных процессах

· При фазовых переходах: DS = ⁿ^DH^ф^.п. .

Т ф.п.

При химических превращениях: DS_х_. _р_. = ån_i × S_i _(кон)

åⁿ j ^× ^S j (исх) ^.

i =1

j =1

При нагревании вещества: DS = C ln

T₂

;

DS = C

T₂

T₁

При изотермическом расширении газа: DS = nR ln

= nR ln

2.6. Термодинамические функции

Задачей II закона термодинамики является определение возможности направления и предела протекания самопроизвольного процесса. Эти вопросы решаются с помощью характеристических функций.

Термодинамические (характеристические) функции – это такие функции, с помощью которых или их производных можно определить состояние системы, т. е. возможен ли в ней самопроизвольный процесс.

Таких функций пять. Каждая из них определяет состояние системы при определенных условиях протекания процесса. Это: внутренняя энергия (U), энтальпия (H), энтропия (S), свободная энергия Гельмгольца (F), свободная энергия Гиббса (G). Эти функции связаны между собой:

Н = U + pV F = U – TS

G = H – TS+ U + pV – TS = F + pV.

Чтобы определить направление процесса нужно знать изменение функций в процессе dH, dU, dS, dF, dG.

2.7. Свободная энергия Гиббса и Гельмгольца

Для изолированной системы изменение энтропии, сопровождающее процесс, позволяет предсказать, будет ли реакция обратимой или необратимой. Как было показано, изменение энтропии положительно, если процесс самопроизвольный, и равно нулю, если процесс обратимый. Эти критерии не могут быть использованы для закрытых систем, для которых направленность процессов оценивается с помощью свободной энергии Гиббса (G) и свободной энергии Гельмгольца (F).

Функция G также называется изобарно-изотермическим потенциалом или

изобарным потенциалом.

При постоянных температуре и давлении: если G = 0, то система находится в

состоянии равновесия; G < 0 – критерий необратимости процесса (т.е.

самопроизвольного процесса).

Функция F называется изохорно-изотермическим потенциалом или изохорным

потенциалом.

При постоянных температуре и объеме при равновесии F = 0; а при

самопроизвольном течении процесса – F < 0.

Изменение свободной энергии Гиббса можно вычислить двумя способами:

1) используя формулу: DG₂₉₈ = DH₂₉₈ -TDS₂₉₈, предварительно определив тепловой

эффект реакции DH₂₉₈ и изменение энтропии DS₂₉₈ ;

2) по стандартным изобарным потенциалам образования вещества ( DG₂₉₈ ):

DG298 = ån i × DG298(кон)

i=1

- ån j × DG298(исх) j =1^N

2.8. Химический потенциал и общие условия равновесия систем

Химический потенциал μ есть функция, определяющая направление и предел самопроизвольного перехода данного компонента из одной фазы в другую при соответствующих превращениях.

Для открытых систем, когда равновесные процессы, протекающие в системе, сопровождаются изменением массы веществ:

dU = TdS - pdV + åmi dni ,

dH = TdS +Vdp + åmi dni ,

dF = -SdT - pdV + åm_i dn_i ,

dG = -SdT +Vdp + åmi dni .

где åm_i dn_i = m₁dn₁ + m₂dn₂ + ... + m_ndn_n

и dn_i - изменение массы i-го компонента; m_i - его

химический потенциал.

Для того, чтобы выразить m_i найдем частную производную:

¶U

¶H

¶F

¶G ö

m = ç

¶n

øS ,V ,n _j ¹1

øS , P,n ¹1

øT ,V ,n ¹1

øT , P,n ¹1

m₁ - частная производная термодинамической функции по массе 1-го компонента при

постоянстве естественных переменных этой функции и массы всех остальных компонентов. Чаще всего процесс ведут при постоянных р и Т, то в расчете используют подчеркнутую формулу.

Так как при самопроизвольном процессе dG < 0, то и m_i < 0 . В самопроизвольном

процессе химический потенциал уменьшается, т. е. компонент может переходить из фазы с большим химическим потенциалом в фазу с меньшим химическим потенциалом.

Вопросы для самоконтроля

1. Дайте формулировки второго и третьего законов термодинамики.

2. Является ли энтропия функцией состояния?

3. Напишите уравнения, характеризующие изменение энтропии в изобарном, изохорном и изотермическом процессах.

4. В каком соотношении находятся молярные энтропии вещества в трех агрегатных состояниях: парообразном, жидком, твердом?

5. В изолированной системе самопроизвольно протекает химическая реакция с образованием некоторого количества конечного продукта. Как изменяется энтропия такой системы?

6. К какому значению стремится энтропия идеального кристалла при приближении температуры к абсолютному нулю?

7. Какие функции называются термодинамическими? Дайте определение и приведите примеры.

8. При каких постоянных термодинамических параметрах изменение энтальпии Н может служить критерием направления самопроизвольного процесса? Какой знак Н в этих условиях указывает на самопроизвольное течение процесса?

9. Критерием направленности каких процессов, протекающих в закрытых системах, являются изобарно-изотермический потенциал и изохорно-изотермический потенциал?

Каковы знаки G и F в условиях протекания самопроизвольного процесса?

10. Как изменяется химический потенциал компонента при самопроизвольном процессе?

11. В результате расширения 20 кг гелия при температуре 298 К объем газа увеличился в 1000 раз. Рассчитайте изменение энтропии. (Ответ: 574,3 кДж/К).

12. Рассчитайте изменение энтропии при нагревании 8 кг метана от 300 К до 500 К при постоянном давлении. Изобарная теплоемкость метана равна 37,51 Дж/(моль^žК). (Ответ: 9,58 кДж/К).

13. Определить изменение энтропии при плавлении 1 моль льда (DНпл = 6009,4 Дж/моль; Т

= 273 К = const). (Ответ: 22 Дж/К).

14. Зная абсолютные энтропии С, Н2, О2 и этанола (S^° С(графит) = 5,694 Дж/моль×К; S^° Н2(г)

= 130,58 Дж/моль×К; S^° О2(г) = 205,02 Дж/моль×К; S^° С2Н5ОН(ж) = 160,67 Дж/моль×К),

определить стандартное изменение энтропии при образовании этанола согласно уравнению

2С(графит) + 3Н2(г) +1/2О2(г) → С2Н5ОН(ж).

15. Для некоторой реакции Н^º = 100 кДж/моль, а S^º = 40 Дж/(моль^žК). При какой

температуре установится равновесие, если Н^º и S^º от температуры не зависят? (Ответ: 2500 К).

Лекция 3

ТЕРМОДИНАМИЧЕСКИЕ СВОЙСТВА РАСТВОРОВ.

РАВНОВЕСИЯ В ГЕТЕРОГЕННЫХ СИСТЕМАХ

3.1. Общая характеристика растворов

Раствором называется термодинамически устойчивая гомогенная система, состав которой может меняться непрерывно в некоторых пределах, определяемых

растворимостью компонентов. Растворимостью компонента называется концентрация насыщенного раствора этого компонента.

Образование раствора из компонентов – процесс самопроизвольный. Процесс растворения как самопроизвольный процесс, протекающий в открытой системе при р = const, T = const, сопровождается убылью энергии Гиббса ( G < 0). Процесс растворения будет протекать до тех пор, пока в системе не установится равновесие ( G = 0). При равновесии химический потенциал индивидуального компонента и его химический потенциал в растворе равны.

Свойства растворов существенно зависят от его состава. Поэтому важной характеристикой раствора является концентрация его компонентов.

1. Массовая доля (Wi) – отношение массы растворенного вещества к общей массе раствора:

W_i = _n^mⁱ

åmi

i=1

2. Мольная доля (Xi) – отношение числа моль ni компонента к общему числу молей раствора:

_X₌ ni

ⁱåni

3. Молярная концентрация (СМ), моль/л – число моль растворенного вещества в 1

л раствора:

CM = ^m

V × M

где m – масса растворенного вещества, г; М – молярная масса растворенного вещества, г/моль; V – объем раствора, л.

4. Моляльная концентрация (Ст), моль/1000 г раст-ля – число моль растворенного вещества в 1000 г растворителя:

_C_m ₌ mв-ва ×1000

mр-ля × М в-ва

3.2. Термодинамические условия образования идеальных растворов

В истинных растворах растворенное вещество находится в молекулярно-дисперсном состоянии (в виде молекул). Между компонентами раствора существует физическое и химическое взаимодействие. Если энергия взаимодействия между однородными молекулами равна энергии взаимодействия между разными молекулами (UAA = UBB = UAB), то такие растворы называются идеальными.

С термодинамической точки зрения идеальный раствор определяется как раствор, обладающий при постоянных значениях давления и температуры следующими термодинамическими свойствами.

1. При образовании идеального раствора не выделяется и не поглощается теплота

( DH смеш.=0).

2. Образование идеального раствора происходит без изменения объема, т.е. объем смеси равен сумме объемов исходных компонентов (Vсмеси= VA+VB ).

3. Изменение химического потенциала компонента раствора равно

где Хi – мольная доля компонента.

4. Изменение энтропии в процессе образования идеального раствора равно

5. Изменение энергии Гиббса при образовании идеального раствора равно

Поскольку мольные доли компонентов в растворе всегда меньше единицы (Хi < 1), то при образовании идеального раствора происходят увеличение энтропии

(), уменьшения химического потенциала () и энергии Гиббса

( ), что свидетельствует о самопроизвольном характере процесса образования раствора. Растворы, для которых не выполняется хотя бы одно из перечисленных выше условий, называют неидеальными (реальными).

3.3. Закон Рауля

При смешивании двух летучих компонентов раствор и пар над раствором содержат оба компонента. Причем пар над раствором может быть как идеальным, так и неидеальным. Для идеального пара концентрация в паре выражается через парциальные давления Рi, а для неидеального пара - через парциальные летучести fi. Уменьшение содержания каждого компонента в растворе вследствие взаимного разбавления вызовет понижение давления насыщенного пара компонента Рi над раствором по сравнению с давлением пара чистого вещества Рi^º. Чем больше вещества содержится в растворе, тем больше давление его насыщенного пара. Эту зависимость, экспериментально установил и сформулировал в 1886 г. французский ученый Ф. Рауль:

Парциальное давление компонента над раствором пропорционально его мольной доли в растворе.

P_i = P_i X _i

Идеальные растворы подчиняются закону Рауля во всем диапазоне концентраций. Для идеального бинарного раствора парциальное давление каждого компонента

равно:

Р1=Р1^ºХ1 и Р2=Р2^ºХ2.

Для чистых компонентов Х1=1 и Х2 =1,тогда Р1=Р1^º и Р2=Р2^º.

Общее давление пара над раствором равно Робщ = Р1 + Р2.

Рассмотрим свойства растворов нелетучих веществ в летучих растворителях. Если растворенное вещество нелетучее (компонент 2), то над раствором присутствуют только пары растворителя (компонент 1). Для таких растворов закон Рауля применим только для растворителя, и формулируется следующим образом: Относительное

понижение давления насыщенного пара растворителя над раствором равно мольной доле растворенного вещества в растворе.

Математически это можно записать в виде:

^P¹⁰_P^-₁₀ ^P¹ = X ₂

Как следует из полученного уравнения, относительное понижение давления насыщенного пара растворителя над раствором зависит только от концентрации растворенного вещества и не зависит от его природы.

3.4. Понижение температуры замерзания растворов

Криоскопия – явление понижения температуры замерзания раствора по сравнению с чистым растворителем.

Явление криоскопии описывается уравнением:

DT_зам = К × т,

где DT_зам = Т_зам₍ _р _-_ля₎ -Т_зам₍ _р _- _ра₎ ; т – моляльная концентрация раствора; К – криоскопическая постоянная. К – некоторая гипотетическая величина. По физическому смыслу криоскопическая постоянная равна понижению температуры замерзания

одномоляльного раствора ( m = 1 Þ DT_зам = К.)

Криоскопическая постоянная не зависит от природы растворенного вещества, а зависит только от природы растворителя и может быть рассчитана по уравнению:

K =		RT ²,пл	, L =	lпл	.
	1000 × L
				М

Т _,пл - температура замерзания чистого растворителя; L - удельная теплота плавления

чистого растворителя; l_{п л} - молярная теплота плавления чистого растворителя; М - молекулярная масса растворителя.

Явление криоскопии используется для определения молекулярной массы растворенного вещества (например, при синтезе нового вещества – оно может быть в виде отдельных молекул или ассоциатов).

DTзам = K	m₂ ×1000	Þ M 2	=	K × m₂ ×1000	,

	M 2 × m1			DTзам × m1

m₂ - масса растворенного вещества, г; m₁ - масса растворителя, г.

3.5. Повышение температуры кипения растворов

Эбуллиоскопия – явление повышения температуры кипения раствора по сравнению с чистым растворителем.

Явление эбуллиоскопии описывается уравнением:

DT_кип = Е × т,

где DТ_кип = Т_кип₍ _р _- _ра₎ -Т_кип₍ _р _- _ля₎ ; m - моляльная концентрация раствора; Е - эбуллиоскопическая постоянная. Физический смысл эбуллиоскопической постоянной: Е – есть повышение температуры кипения одномоляльного раствора

( m =1 Þ DTкип = E ).

Эбуллиоскопическая постоянная не зависит от природы растворенного вещества, а зависит от природы растворителя и определяется по формуле:

E =		R ×T ²	; L =	l
				исп

	1000 × L_исп		исп	М
	1000 × L_исп			М

Явление эбуллиоскопии используется для определения молекулярной массы растворенного вещества (М2).

DTкип = K	m2 ×1000	Þ M 2	=	K × m2 ×1000	,

	M 2 × m1			DTкип × m1

m₂ - масса растворенного вещества, г; m₁ - масса растворителя, г.

3.6. Осмос и осмотическое давление

Осмос – процесс самопроизвольного перехода вещества через полупроницаемую мембрану под действием градиента концентрации.

Запишем химический потенциал растворителя в растворе и в чистом растворителе

m ^р ^- ^ль = m + RT ln P

р - ль1

m ^р ^- ^р = m + RT ln P ,

р - ль1

где P₁ - давление пара чистого растворителя; P1 = P1 × Х1 - давление пара над раствором. Так как P₁ < P₁ , то и m_р^р_-^-_ль^ль > m_р^р_-^-_ль^р . В связи с этим термодинамически

растворитель должен переходить из фазы с большим химическим потенциалом в фазу с меньшим химическим потенциалом, а именно, растворитель через мембрану переходит в раствор и разбавляет его. Тем самым уровень в капилляре будет подниматься.

Сила, заставляющая переходить растворитель через мембрану в раствор, называется осмотическим давлением.

По мере увеличения высоты столба в капилляре возрастает гидростатическое давление, противодействующее осмотическому давлению. Когда гидростатическое давление станет равным осмотическому, в системе установится равновесие. В момент равновесия химические потенциалы растворителя в чистом растворителе и в растворе становятся равными.

_m р - ль ₌ _m р - р		Þ P = P + p ,
р - ль	р - ль	11

где p - осмотическое давление.

Величина осмотического давления π зависит от молярной концентрации (С) и температуры (Т) для предельно разбавленных растворов, и эта зависимость описывается уравнением Вант-Гоффа:

p = CRT ,

где R – универсальная газовая постоянная.

Осмос и осмотическое давление имеют большое значение в жизни различных организмов. Особенно наглядно явление осмоса наблюдается в клетках растительных организмов.

1.7. Ограниченная взаимная растворимость жидкостей

В зависимости от природы жидкостей, составляющих систему, различают:

· нерастворимые друг в друге жидкости (ртуть и вода, бензин и вода);

· ограниченно растворимые друг в друге жидкости (вода и анилин, вода и фенол);

· неограниченно растворимые жидкости, образующие однородный раствор (вода

и этиловый спирт, вода и уксусная эссенция).

Рассмотрим системы с ограниченной растворимостью двух жидкостей. Диаграммы состояния таких систем представлены на рис. 3.1.

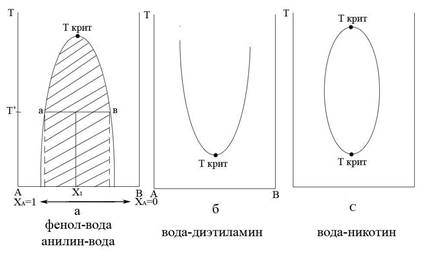
Рис. 3.1. Диаграммы состояния с ограниченной растворимостью жидкостей:

а – с верхней критической точкой; б – с нижней критической точкой;

с – с верхней и нижней критическими точками

Кривая разделяет области существования гомогенных и гетерогенных систем. Заштрихованная площадь – это область расслаивания жидкостей (двухфазная). Ветвь а

– представляет собой насыщенный раствор В в А. Ветвь в – насыщенный раствор А в В. Для определения состава жидкостей, находящихся при температуре Т в равновесии, необходимо провести ноду ав. Опустив из точки а и точки в перпендикуляры на ось, определяем состав двух жидкостей.

Критическая точка (температура) – это температура, выше или ниже которой жидкости неограниченно растворимы. Для нахождения критической точки используют правило прямолинейного диаметра Алексеева. Через каждую полученную точку проводят ноду. Через середины нод проводят прямую линию. Точка пересечения этой прямой с кривой и является критической точкой.

Вопросы для самоконтроля

1. Понятие раствора. Термодинамические условия образования раствора.

2. Способы выражения концентрации растворов.

3. Какой раствор называют идеальным. Условия образования идеального раствора.

4. Сформулируйте закон Рауля для компонента идеального раствора. Как влияет увеличение концентрации раствора на давление насыщенного пара?

5. Какие растворы в термодинамике называются предельно разбавленными?

6. Дайте определение явлениям криоскопии и эбуллиоскопии.

7. Приведите уравнение для расчета осмотического давления идеального раствора.

8. Как влияет степень электролитической диссоциации растворенного вещества на изменение температуры замерзания и температуры кипения раствора?

9. Явление ограниченной взаимной растворимости двух жидкостей. Типы диаграмм взаимной растворимости с различным положением критической точки.

10.Чему равна температура кипения 10 % раствора сахарозы С12Н22О11? Эбуллиоскопическая постоянная воды равна 0,52. (Ответ: 100,17 ºС).

11.Раствор, содержащий 5 г неэлектролита в 100 г воды замерзает при температуре -1,5 ºС. Вычислите молекулярную массу неэлектролита. (Ответ: 60 г/моль).

12.Рассчитайте осмотическое давление 0,01 М водного раствора сульфата натрия при температуре 300 К, если степень диссоциации Na2SO4 равна 0,88 (Ответ: 69 кПа).

13.Давление пара воды при 25 ^оС составляет 3167 Па. Вычислите давление пара раствора, содержащего 90 г глюкозы в 450 г воды. (Ответ: 3105 Па).

14.При концентрации хинона (моль/л) в воде 0,002915 и 0,008415, а в этиловом эфире соответственно 0,00893 и 0,02714 определите коэффициент распределения хинона между водой

и этиловым эфиром. (Ответ: 0,3182).

Лекция 4

ХИМИЧЕСКОЕ РАВНОВЕСИЕ

4.1. Закон действующих масс. Признаки химического равновесия

В общем виде любую обратимую химическую реакцию можно написать:

аА + вВ ⇆ сС + dD

Согласно закона действующих масс: скорость химической реакции пропорциональна действующим массам реагирующих веществ.

Тогда выражения для скорости прямой ( v ) и скорости обратной ( v ) реакции имеют следующий вид:

₌ав₌сd

v kпрСАСВ , v kобрСССD ,

где kпр kобр – константы скорости прямой и обратной реакций .

В ходе реакции концентрация исходных веществ уменьшается, вместе с этим уменьшается и скорость прямой реакции. Одновременно увеличивается концентрация продуктов реакции и вместе с ними растет скорость обратной реакции. Наступает момент, когда скорость прямой реакции становится равной скорости обратной реакции

		обратимой						реакции называется *химическим*
(v	= v) . Такое состояние химической	обратимой						реакции называется *химическим*
*равновесием.*
	k С^аС^в = k С^с							С^d
	пр	А В			обр		С	D
		=	^kпр		=	С^с С ^d
	^KC						С	D	,
	^KC		k						,
			k	обр		_C а_Св
				обр			А	В

где КС – константа химического равновесия, равная отношению констант скоростей прямой и обратной реакций.

Таким образом, отношение произведения концентрации продуктов реакции, взятых

в степенях равных их стехиометрическим коэффициентам, к произведению концентрации исходных веществ, взятых в степенях равных их стехиометрическим коэффициентам, есть величина постоянная, и называется константой равновесия.

Константа равновесия связывает равновесные концентрации всех веществ, участвующих в реакции. При этом концентрация ни одного из веществ не может быть изменена так, чтобы концентрации всех остальных веществ остались неизменными при данном значении константы равновесия в конкретных условиях. То есть константа равновесия не зависит от концентрации.

4.2. Способы выражения константы равновесия

Для конденсированных систем чаще всего используют константу равновесия, выраженную через концентрации (КС).

Для гомогенных газовых систем константа равновесия записывается через парциальные давления рi (Kp), молярные концентрации Сi (КС), мольные доли Хi (КХ).

Для реакции аА + вВ ⇆ сС + dD в газовой фазе константы равновесия можно записать:

= _C ^d _C^c

K_C ^D ^C

C_A^aC_В^в

= _P^d _P^c

K_P ^D ^C

P_A^a P_В^в

= _X ^d _X ^c

K _X ^D ^C

X _A^a X _В^в

(V = const);

(P = const);

(Т = const).

Константы равновесия связаны между собой следующим образом:

K == K (RT )^Dⁿ = К Р^Dⁿ

P C Х общ

где Dn - изменение числа моль только газообразных реагентов в результате реакции.

4.3. Уравнение изотермы химической реакции

Для определения возможности и направления протекания химической реакции используют уравнение изотермы химической реакции:

= -RT ln K

+ RT ln

ÕP_iⁿ i

кон

x. p.

i =1

Õ pⁿ_j

исх

j =1

Например, для реакции N2 + 3H2 ⇆ 2NH3

P²

P¢²

^D^Gx. p.

= -RT ln

NH₃

+ RT ln

NH₃

_P3

P¢ P¢³

N ₂

N ₂ H ₂

где P_NH₃ , P_N ₂ , P_H ₂ - парциальные давления

компонентов

в момент равновесия;

P_NH¢₃ , P_N¢₂ , P_H¢₂ - парциальные давления компонентов в любой момент времени, в том числе и в момент равновесия.

Соотношение этих слагаемых определяет знак G. Если G<0, то реакция идет

преимущественно в прямом направлении. При G>0 – в сторону исходных веществ, а при G=0 – имеет место равновесие.

Если P¢=1, то ln1 = 0, тогда

DG_x_. _p_. = -RT ln K_P .

Уравнение связывает стандартное изменение энергии Гиббса химической реакции с константной равновесия. Это очень важный результат, так как DG можно рассчитать из термодинамический данных, а, следовательно, не проводя экспериментального исследования равновесия, можно вычислить K _P

4.4. Термодинамическая теория химического сродства

Под химическим сродством понимают способность веществ к химическому взаимодействию. Химическое сродство у разных веществ различно и зависит от ряда факторов: природы реагирующих, концентрации (или давления), температуры и др. Чем больше химическое сродство, тем полнее идет химическая реакция. Химическое сродство является критерием осуществимости той или иной реакции.

Химическое сродство веществ непосредственно измерить нельзя. Мерой химического сродства является максимальная полезная работа Wmax, которая может быть получена в результате реакции между веществами. При постоянных значениях давления и температуры Wmax = ̵ GP,T, а при постоянных значениях объема и температуры Wmax = ̵ FV,T. Эти соотношения вытекают из второго закона термодинамики.

Если участники реакции находятся состоянию идеального газа в отдельных стандартное изменение энергии Гиббса:

DG_x_. _p_.

в стандартном состоянии (т.е. отвечают сосудах при давлении 1атм), то получаем

= -RT ln K_P

Величину ̵ G^º называют стандартным химическим сродством.

4.5. Смещение химического равновесия

Смещение химического равновесия, т. е. переход из одного равновесного состояния

к другому, отвечающему измененным условиям, подчиняется правилу, которое называется принципом Ле-Шателье (или принципом подвижного равновесия) (1884):

Если на систему, находящуюся в состоянии равновесия, оказывать внешнее воздействие, то равновесие смещается в сторону преимущественного протекания той реакции, которая ослабляет произведенное воздействие.

На химическое равновесие оказывают влияние температура, давление (в том случае, если реакция протекает с участием газообразных веществ), изменение концентрации.

· От температуры зависят константы равновесия КР и КС.

Зависимость КР и КС от температуры выражаются уравнением изобары химической реакции или уравнением изобары Вант-Гоффа:

æ d ln K P ö

ç ÷

è dT ø_P

и уравнением изохоры химической реакции:

æ d ln KC ö

ç ÷

è dT ø_V

₌DH RT ²

₌DU RT ²

Дифференциальная форма уравнений позволяет определить только общий характер зависимости константы равновесия от температуры.

Проанализируем уравнение изобары химической реакции.

1) DH > 0 (прямая реакция эндотермическая)

R > 0,T > 0 Þ	¶ ln K _p	> 0 Þ T K		, т. е. при увеличении температуры
R > 0,T > 0 Þ		> 0 Þ T K	P	, т. е. при увеличении температуры
	¶T		P
	¶T

равновесие смещается в сторону прямой реакции, а именно, эндотермической реакции.

2) DH < 0 (прямая реакция экзотермическая)

R > 0,T

равновесие реакции.

> 0 Þ	¶ln K_P	< 0 Þ T K		¯ , т.	е. при	увеличении температуры
	¶T		P


смещается в		сторону обратной			реакции, а	именно, эндотермической

Следовательно, увеличение температуры смещает равновесие в сторону эндотермической реакции (идущей с поглощением тепла). Уменьшение температуры сдвигает равновесие в сторону экзотермической реакции (идущей с выделением тепла).

Уравнение изобары в интегральном виде:

	K P2	=	DH æ		1	-	1 ö
ln				ç				÷
	K P1		R
				è T1			T2 ø

	K P2	=	DH æT2 -T1			ö
или ln				ç		÷
или ln	K P		R	ç	T1T2	÷
	1			è		ø

От давления не зависят константы равновесия КР и КС, а зависит только КХ. Эта зависимость описывается уравнением Планка-Ван-Лаара:

æ d ln K X ö

= -

è dP

ø_T

Проанализируем это уравнение.

n=(c+d) - (a+в)

æ ¶ln K

Dn = 0,ç

= 0 Þ K _X

не зависит от давления.

¶P

øT

¶ln K

Dn > 0 Þ V

> V

; P > 0 Þ ç

< 0 Þ P K

¯ , т. е. при увеличении

кон

исх

¶P

ø_T

давления равновесие смещается в сторону обратной реакции, а именно, в сторону исходных веществ, занимающих меньший объем.

			æ ¶ln K		X	ö
3)	Dn < 0 Þ V	> V ; P > 0 Þ ç			X	÷	> 0 Þ P K		, т. е. при увеличении
3)	Dn < 0 Þ V	> V ; P > 0 Þ ç				÷	> 0 Þ P K	X	, т. е. при увеличении
	исх	кон	è	¶P		ø_T		X
			è	¶P		ø_T

давления равновесие смещается в сторону прямой реакции, а именно, в сторону конечных веществ, занимающих меньший объем.

Следовательно, при увеличении давления равновесие смещается в сторону меньшего объема.

= _C^c _C ^d

Для химической реакции аА + вВ ⇆ сС + dD константа равновесия KC C D не

C_A^aC_B^в

зависит от концентрации реагирующих веществ. От концентрации зависит положение равновесия.

При увеличении концентрации одного из веществ равновесие смещается в направлении той реакции, при которой это вещество расходуется. При достижении нового равновесия константа будет иметь точно такое же значение.

При увеличении концентрации исходных веществ равновесие смещается в сторону прямой реакции, а именно, в сторону продуктов реакции.

При увеличении концентрации конечных веществ равновесие смещается в сторону обратной реакции, а именно, в сторону и исходных веществ.

Вопросы для самоконтроля

1. Признаки химического равновесия. Что называется константой равновесия? Виды констант равновесия в конденсированных и газообразных системах.

2. Как связаны константы равновесия Кр, КС и КХ реакции, протекающей в смеси идеальных газов температуре Т и общем давлении Р. Покажите эту связь для реакции 2SO2(г) +

O2(г)^D 2SO3(г).

3. Напишите уравнение изотермы химической реакции.

4. Что называется химическим сродством веществ? Что является мерой химического сродства?

5. Для некоторой химической реакции в газовой фазе при постоянных значениях давления

и температуры найдено GТ >0. В каком направлении самопроизвольно протекает эта реакция?

6. Напишите уравнение, связывающее стандартное химическое сродство и константу равновесия КР при постоянных значениях давления и температуры.

7. Как влияет температура на константы равновесия КР и КС? Что является мерой этого влияния? Напишите уравнения изобары и изохоры химической реакции.

8. Напишите уравнение, отражающее зависимость константы равновесия КХ от давления,

и проанализируйте его.

9. Определить при температуре 500 К направление протекания процесса:

	2CO(г) + 2H2(г)^DCH4(г)+CO2(г)
при следующих условиях: K = 2,57×10 ^-8,			P	= 1,013×10⁴,	P	= 2,026 ×10⁴	,
	P		CO		^H2
	P	= 2,026 ×10⁴ , P			= 5,07 ×10⁴ н / м² ,
	CH₄			CO₂
10. Рассчитайте стандартное сродство			G^º298 для реакции 2NO + O2 ^D 2NO2 ( G^º298(NO) =
87,58 кДж/моль,	G^º298(NO2) =	52,29		кДж/моль)	и	определите	направление ее

11. Как нужно изменить температуру, давление и концентрацию Cl2, чтобы сместить химическое равновесие в сторону прямой реакции?

2Cl2(г) + H2O(г) ^D 4HCl(г) + O2(г)

Лекция 5

ХИМИЧЕСКАЯ КИНЕТИКА

5.1. Скорость химической реакции

Химическая кинетика представляет собой учение о скоростях химических реакций, о факторах, определяющих эти скорости (природы реагирующих веществ, концентрации, температуры, присутствия катализаторов и др.), а также о механизме химических реакций.

Скоростью химической реакции называется изменение количества одного из реагирующих веществ в единицу времени в единице объема, а для реакций при постоянном объеме - изменение концентрации одного из реагирующих веществ в единицу времени. Различают среднюю и истинную скорости:

n = ± ^D_D^c_t

n = ± _V^dn_×_dt = ± ^dc_dt

В выражение скорости по исходному веществу ставят знак минус, а по продукту

реакции – плюс. Пусть имеется реакция: аА + вВ ⇆ сС + dD, тогда

n A = - ^dc^A ,n B = - ^dc^B ,nC = ^dc^C ,n D = ^dc^D
dt	dt	dt	dt

Между скоростями, определенными по различным веществам, существует связь:

dc_A

= -

dc_B

dc_C

dc_D

а dt

b dt

c dt

d dt

n A =

n B =

nC =

n D

5.2. Зависимость скорости реакции от концентрации.

Порядок и молекулярность реакции

Скорость реакции зависит от ряда факторов (природы реагирующих веществ, концентрации, температуры и др.).

Сформулируем основной постулат химической кинетики, определяющий зависимость скорости реакции от концентрации реагирующих веществ: Скорость химической реакции пропорциональна концентрации реагирующих веществ, взятых в некоторых степенях.

Например, если реагируют вещества А и В, то

n = kCAⁿ ×C_B^p .

Коэффициент пропорциональности k называется константой скорости химической реакции и численно равен скорости при концентрациях реагирующих веществ, равных единице. Размерность k зависит от природы реагирующих веществ, равных единице. Размерность k зависит от природы реакции [k]=время^-1·конц^1-r. Показатели степени (n,p), в которые возведены концентрации соответствующих веществ (сА и сВ), называются порядком реакции по соответствующему веществу. Общий порядок равен

сумме порядков реакций по каждому веществу или сумме показателей степеней r = n + p.

Порядок может быть целым, дробным, положительным, отрицательным и даже нулевым. Для очень многих реакций, даже сравнительно простых реакций, порядок не совпадает со стехиометрическим коэффициентом. Это объясняется тем, что реакции протекают обычно по сложным механизмам в несколько стадий, которые не находят отражения в химических уравнениях. Порядок реакции понятие формальное, поскольку

в большинстве случаев не отражает механизма реакции. Определяется порядок реакции экспериментально и отражает зависимость скорости реакции от концентрации вещества.

Для элементарных реакций вместо порядка реакции говорят о её молекулярности. Молекулярность реакции равна числу частиц (молекул, радикалов, атомов), принимающих участие в элементарной реакции или элементарном акте реакции. Молекулярность реакции всегда целочисленна, положительна и не превышает трех.

Период полупревращения – это период времени, необходимый для того, чтобы концентрация исходного вещества уменьшилась вдвое (t1/2).

5.3. Формальная кинетика реакций различных порядков

Рассмотрим кинетические уравнения односторонних реакций, порядок которых дается целым числом. Выражения константы скорости, времени и периода полупревращения реакций нулевого, первого и второго порядков представлены в виде таблицы.

Таблица 5.1. Формальная кинетика реакций различных порядков

порядок	константа скорости k,	время t	период
реакции	размерность		полупревращения t1/2

нулевой

k =

- cA

é моль ù

t =

- cA

t1/ 2

л × с

ln 2

первый

k =

×ln

, [с^-1 ]

t =

×ln

t1/ 2

л ù

æ 1

t1/ 2 =

второй

k =

×ç

÷,

t =

×ç

÷,

k ×c_A

è cA

ë моль ×с û

è cA

CAº – начальная концентрация вещества А; СА – текущая концентрация вещества А в момент времени t.

Зная порядок реакции, можно рассчитать константу скорости и сделать предположение относительно механизма протекания реакции. Рассмотрим наиболее часто используемые способы определения порядка.

1. Способ подстановки. Экспериментальные результаты поочерёдно подставляют

в уравнения константы скорости реакции различных порядков. Если использование одного из этих уравнений даёт постоянную величину константы скорости, реакция имеет соответствующий порядок. Если одинаковые значения не получаются, то реакция имеет дробный порядок или сложный характер.

2.Графический способ. Строят графики зависимости концентрации от времени в различных координатах (СA-t; lnCA-t; 1/CA-t). Там, где получилась прямая, таков и порядок реакции.

3.Способ Оствальда-Нойеса. Основан на определении прядка реакции по периоду полупревращения. Для реакции n-го порядка было получено выражение

t₁		=	₂n -1	-1	=	A	. Логарифмируя это выражение, имеем: lg(t1/2) = lgA - (n-1)lgC.
t₁	2	=	(n -1)k C ⁿ ^-¹		=	_C n -1
	2		(n -1)k C ⁿ ^-¹			_C n -1
				n

Отсюда следует, что зависимость логарифма периода полупревращения от логарифма начальной концентрации вещества представляет собой прямую линию, для которой tga = (n-1). Отсюда n =1- tga.

4.Способ Вант-Гоффа. Необходимо знать две скорости реакции при двух различных концентрациях веществ. v1 = kCA1ⁿ и v2 = kCA2ⁿ. Тогда

		n		C_Aⁿ										lg		v₁
		n								^CA				lg
v	=	kC_A	=					v	= n lg	^CA			Отсюда n =			v
1				1	.	Прологарифмируем:	lg	1			1	.			2		.
1					.	Прологарифмируем:	lg	1				.					.
v		kCⁿ		C ⁿ				v		C	A			lg	C_A
2		A		A				2			A				1

		2		2							2				^CA
		2		2							2				2
															2

Графический вариант метода Вант-Гоффа: v=k·CAⁿ. После логарифмирования получаем: lgv=lgk+n·lgCA. Порядок реакции n определяют как tg угла наклона прямой в координатах lgv от lgCA.

5.4. Зависимость скорости реакции от температуры

Эксперименты показывают, что с увеличением температуры скорость химической реакции (константа скорости) быстро растет. Согласно приближенному правила Вант-Гоффа: при повышении температуры на 10 ºС скорость гомогенной реакции увеличивается в 2-4 раза:

_g ₌ kТ +10 _.

kТ

где g - температурный коэффициент скорости реакции; kT+10 и kT – константы скорости реакции соответственно при температурах T+10 и T.

При увеличение температуры от Т1 до Т2 правило Вант-Гоффа имеет вид:

g n =	kТ2	, где	n =	T2 -T1	.

	kТ1		10

С. Аррениус (1889) установил более точную зависимость константы скорости химической реакции от температуры:

d ln k	=	E		,
dT		RT	2

где E - энергия активации реакции.

После интегрирования уравнения в интервале температур от T1 до T2 получается следующее выражение:

ln	kT2	=	E æ 1		-	1	^ö.
				ç
	kT1						÷
			R è T1			T2 ø

Вопросы для самоконтроля

1. Какие реакции называются обратимыми? Признаки химического равновесия.

2. Что называется константой равновесия? Виды констант равновесия в конденсированных и газообразных системах.

3. Как связаны константы равновесия Кр, КС и КХ реакции, протекающей в смеси идеальных газов температуре Т и общем давлении Р. Покажите эту связь для реакции 2SO2(г) +

O2(г)^D 2SO3(г).

4. Напишите уравнение изотермы химической реакции.

5. Что называется химическим сродством веществ? Что является мерой химического сродства?

6. Для некоторой химической реакции в газовой фазе при постоянных значениях давления

и температуры найдено GТ >0. В каком направлении самопроизвольно протекает эта реакция?

7. Напишите уравнение, связывающее стандартное химическое сродство и константу равновесия КР при постоянных значениях давления и температуры.

8. Каким образом можно сместить химическое равновесие? Сформулируйте принцип Ле Шателье.

9. Как влияет температура на константы равновесия КР и КС? Что является мерой этого влияния? Напишите уравнения изобары и изохоры химической реакции.

10. Напишите уравнение, отражающее зависимость константы равновесия КХ от давления,

и проанализируйте его.

11. Определить при температуре 500 К направление протекания процесса:

	2CO(г) + 2H2(г)^DCH4(г)+CO2(г)
при следующих условиях : K = 2,57×10 ^-8, P			CO	= 1,013×10⁴,		P = 2,026 ×10⁴	,
	P		CO			H₂
	P	= 2,026 ×10⁴ , P			= 5,07 ×10⁴ н / м² ,
	CH₄			CO₂
12. Рассчитайте стандартное сродство G^º298 для реакции 2NO + O2 ^D 2NO2 ( G^º298(NO) =
87,58 кДж/моль,	G^º298(NO2) =	52,29	кДж/моль)		и	определите направление ее

13. Как нужно изменить температуру, давление и концентрацию Cl2, чтобы сместить химическое равновесие в сторону прямой реакции?

14. Что называется скоростью химической реакции? Напишите выражение для средней и истинной скорости.

15. Запишите выражение скорости реакции по основному постулату кинетики в общем виде

и для реакции 2NO + O2 = 2NO2.

16. Укажите физический смысл константы скорости. От чего зависит константа скорости?

17. Что такое порядок и молекулярность реакции? Какие значения могут принимать молекулярность и порядок реакции? Какая величина отражает механизм реакции?

18. Какие известны методы определения порядка реакции?

19. Запишите кинетические уравнения реакций первого и второго порядков.

20. Зависимость скорости химической реакции от температуры.

21. Реакция второго порядка, для которой исходные концентрации реагирующих веществ одинаковы, протекает за 10 мин на 25 %. Сколько времени потребуется, чтобы реакция прошла на 50 % при той же температуре? (Ответ: 30 мин).

22. Константа скорости реакции при 300 К равна 0,02 мин^-1, а при 350 К – 0,6 мин^-1. Чему равна энергия активации? (Ответ: Е = 59,4 кДж/моль).

23. Во сколько раз увеличится скорость реакции при увеличении температуры от 298 К до 328 К, если температурный коэффициент реакции равен 3? (Ответ: в 27 раз).

Лекция 6

ЭЛЕКТРОХИМИЯ

Электрохимия – это раздел физической химии, в котором изучается взаимосвязь химических и электрохимических явлений.

Существует два подраздела электрохимии. Это – ионика и электродика. Ионика изучает свойства растворов электролитов. Электродика изучает явления и процессы, протекающие на границе металл (или полупроводник) – электролит.

6.1. Растворы электролитов

Согласно теории Аррениуса, электролиты в водном растворе распадаются на ионы. Такой процесс распада вещества на ионы называется электролитической диссоциацией. Растворы электролитов проводят электрический ток.

К электролитам относятся кислоты, основания, соли, вещества, содержащие сильнополярные связи. По способности образовывать ионы в растворе электролиты делят на две группы: сильные и слабые. Сильными электролитами называются вещества, практически полностью распадающиеся на ионы. Слабые – частично распадающиеся на ионы.

Способность вещества диссоциировать на ионы определяется степенью диссоциации α, которая определяется как отношение числа молекул, распавшихся на ионы, к общему числу молекул.

Степень диссоциации зависит от:

^§Природы электролита: неэлектролиты (α = 0); слабые электролиты (α < 0,03); средние электролиты (0,03 < α < 0,3); сильные электролиты (α > 0,3).

^§Температуры. С повышением температуры степень диссоциации увеличивается

(α~Т).

^§Концентрации. С повышением концентрации степень диссоциации уменьшается.

^§Присутствия одноименных ионов. Степень диссоциации слабого электролита уменьшается, если внести в его раствор сильный электролит с одноименным ионом. Поскольку молекулы не полностью распадаются на ионы, то устанавливается

равновесие между ионами и недиссоциированными молекулами. Для электролита АВ процесс диссоциации можно записать так:

АВ ⇆ А⁺ + В^‾

Равновесие может количественно характеризоваться константой равновесия, называемой в данном случае константой диссоциации.

_К_дис ₌ [А_[⁺ ]×[В_]^- ]

АВ

Кдис зависит от природы электролита и температуры, но не зависит от концентрации. Cвязь константы диссоциации связана со степенью диссоциации, которая

выражается законом разведения Оствальда:

К_дис = ^a ²^С

1 -a

Константа диссоциации не зависит от концентрации или разведения ( V = _C¹ ). Это обусловлено тем, что от концентрации или разведения зависит степень диссоциации.

6.2. Диссоциация воды. Ионное произведение воды. Понятия рН и рОН

Вода является слабым электролитом: Н2О ⇆ Н⁺ + ОН ̄, поэтому

_К_дис ₌ [Н ⁺_[]×[ОН_]^- ]

Н 2О

Степень диссоциации воды очень мала, поэтому [Н2О] величина постоянная и тогда Кдис ^ž[Н2О] = [Н⁺]·[ОН ̄ ] = Кw

Это выражение является ионным произведением воды (Кw), которое не зависит от концентрации, но существенно зависит от температуры.

При Т = 298К Кw=1,008·10^-14 ≈ 1·10^-14.

В нейтральной среде [Н⁺] = [ОН ̄ ] = 10^-7. В кислых растворах [Н⁺] > [ОН ̄ ], поэтому [Н⁺] > 10^-7. Для щелочных растворов характерно: [ОН ̄ ] > [Н⁺], и [Н⁺] < 10^-7. Такими величинами пользоваться неудобно, поэтому были введены понятия рН и рОН.

pH = -lg[H⁺]; pOH = -lg[OH ̄ ]

Если прологарифмировать ионное произведение воды со знаком минус

-lg[H⁺] – lg[OH ̄ ] = 14,

тогда при температуре 298 К получим: рН + рОН = 14.

Кислотность растворов можно охарактеризовать количественно и через величину рН:

· нейтральный раствор рН = 7;

· кислый раствор рН < 7;

· щелочной раствор рН > 7.

Вычисление рН сильных электролитов производят по формуле: pH = lg a_H + , где a_H +

- активность протонов водорода.

6.3. Буферные растворы

Буферными называются растворы, рН которых сохраняются постоянными при разведении, а также при прибавлении небольших количеств кислот или щелочей.

Буферные растворы широко используют в различных химических исследованиях. Буферные растворы имеют большое значение для протекания процессов в живых организмах. Например, в крови постоянство водородного показателя рН (рН = 7,36) поддерживается буферными смесями, состоящими из карбонатов и фосфатов.

Буферные растворы обычно представляют собой смесь растворов:

а) слабая кислота и соль этой кислоты и сильного основания, например СН3СООН + СН3СООNa (уксусная кислота и ацетат натрия); H2CO3 + KHCO3 (угольная кислота и гидрокарбонат калия);

б) слабое основание и соль этого основания и сильной кислоты, например NH4OH + NH4Cl (гидроксид аммония и хлорид аммония);

в) смесь средних и кислых солей, например Na3PO4 + NaH2PO4.

Меняя концентрацию и соотношение растворов можно получить буферные растворы с различным значением рН.

Расчет рН кислотно-основных буферных растворов производят с помощью следующих уравнений:

pH = рКк + lg		Cсоли		; рКк = -lg Kдис(к-ты)
pH = рКк + lg				; рКк = -lg Kдис(к-ты)
	Скислоты
pH = 14 - рКо - lg			Cсоли		; рКо = -lg Kдис(осн-ия)

			Соснования

6.4. Электропроводность растворов электролитов

При наложении внешнего электрического поля на хаотичное тепловое движение ионов накладывается ориентированное поступательное движение к поверхности электродов. На скорость передвижения катионов (νк) и анионов (νа) влияют:

· размер иона: чем меньше ион (гидратированный ион), тем он более подвижен;

· заряд иона: скорость движения тем больше, чем выше его заряд;

· напряженность электрического поля Е (отношение разности потенциалов между электродами к расстоянию между ними); чтобы исключить влияние этого фактора, принято сравнивать абсолютные скорости движения ионов (U+, U-). Абсолютной скоростью иона называют скорость его передвижения в поле с напряженностью

1В/м: U ₊ = ⁿ_E^к ;U _- = ⁿ_E^a ;

· концентрация электролита: с уменьшением концентрации электролита в растворе абсолютные скорости ионов растут;

· температура: при более высокой температуре скорость иона возрастает, так как снижается вязкость раствора;

· аномально высокими значениями абсолютных скоростей в водных растворах обладают ионы Н3О⁺ и ОН ̅. Это принято объяснять особым механизмом движения этих ионов в водных растворах – эстафетным. Между ионами гидроксония Н3О⁺ и молекулами воды Н2О, а также гидроксид-ионами ОН ̅ и Н2О происходит обмен Н⁺. Эти процессы протекают с огромной скоростью – средняя продолжительность существования иона составляет около 10^-11 с. В отсутствие внешнего поля такой обмен протекает в любых направлениях; под действием электрического поля передача ионов Н⁺ происходит направленно.

В растворах электролитов носителями заряда являются как катионы, так и анионы. Для оценки участия данного вида ионов в переносе электричества пользуются понятием числа переноса ионов. Числом переноса ионов называется отношение количества электричества, перенесенного ионами данного вида, к общему количеству электричества, прошедшего через электролит, т. е. числа переноса показывают долю электричества, переносимую данным видом ионов.

Для бинарного электролита числа переноса для катиона и аниона выражаются

следующими уравнениями: t₊ =		U₊	,	t_- =		U_-	.
	U₊ +U_-				U₊ +U_-

Для характеристики способности растворов электролитов проводить электрический ток используют удельную электропроводность (æ), представляющую собой величину, обратную удельному сопротивлению (ρ).

æ =	1	=	l	, _ê^é	м		= Ом^-¹ × м^-¹ =	См	_úù	,
	r		RS		Ом× м	2		м
				ë					û

где R – сопротивление электролита, Ом; S – площадь электродов, м²; l – расстояние между электродами, м.

Удельной электроповодностью называется электропроводность столба жидкости между электродами площадью 1 м² , находящимся на расстоянии 1 м.

При изучении электропроводности растворов целесообразно пользоваться молярной (эквивалентной) электропроводностью (λ).

Молярной электрической проводимостью λ называется электропроводность столба жидкости, содержащегося 1 кмоль электролита, заключённого между электродами, площадью 1 м² и находящимися на расстоянии 1 м друг от друга; [Ом ^-1 · м² · кмоль^-1].

Связь между молярной λ и удельной æ электропроводностью определяется соотношением:

λ = æ / С,

где С – концентрация электролита (кмоль/м³,).

С увеличением разведения (1/С) молярная электропроводность как сильных, так и слабых электролитов возрастает и достигает некоторого предельного значения, которое

называется электропроводностью при бесконечном разведении(λ¥).

Для слабых электролитов отношение эквивалентной электропроводности к эквивалентной электропроводности при бесконечном разведении равно степени диссоциации:

λ/λ∞ = α или λ = αλ∞

Для растворов сильных электролитов при расчёте зависимости эквивалентной электропроводности от концентрации применяется уравнение Кольрауша:

λ = λ∞ – А√C,

где А - константа при данной температуре и для данного растворителя, значение которой тем выше, чем больше заряд ионов, на которые распадается молекула электролита; С- концентрация электролита.

Уравнение Аррениуса: λ = Fα(Uк + Ua) (где F- число Фарадея, α – степень электролитической диссоциации) показывает, что молярная электропроводимость растворов зависит от абсолютных скоростей движения катиона и аниона.

Ф.Кольрауш экспериментально показал, что в предельно разбавленных растворах электролитов каждый ион вносит свой независимый вклад в молярную

электропроводность: λ∞ = λ∞⁺ + λ∞̅,

где λ∞⁺ и λ∞ ̅ - эквивалентная (или молярная) электропроводность катиона и аниона при бесконечном разведении и называются электролитическими подвижностями. Закон был открыт Кольраушем в 1879 г: эквивалентная (молярная) электропроводность бинарного электролита при бесконечном разведении равна сумме электролитических подвижностей катиона и аниона.

При С → 0 α →1 уравнение Аррениуса принимает следующий вид:

λ v = F(Uk+Ua )=FUк+FUa, т.е λ∞⁺ = FUк и λ∞ ̅=FUа

Отсюда электролитическая подвижность иона равна произведению числа Фарадея на абсолютную скорость движения иона.

Вопросы для самоконтроля

1. Растворы сильных и слабых электролитов, отличия их свойств. Степень электролитической диссоциации и константа диссоциации слабого электролита.

2. Буферные растворы и их использование.

3. Ионное произведение воды. Водородный показатель.

4. Закон разбавления Оствальда.

5. Удельная и эквивалентная (молярная) электропроводность, взаимосвязь этих величин.

6. Скорость движения ионов. Числа переноса.

7. Зависимость эквивалентной (молярной) электропроводности от концентрации для сильных электролитов. Уравнение Кольрауша.

8. Объяснить, с чем связана аномально высокая абсолютная скорость движения ионов гидроксония и гидроксид-ионов.

9. Закон независимого движения ионов. Молярная электропроводность при бесконечном

разведении (l¥).

10. Связь молярной электропроводности с абсолютными скоростями движения катиона и аниона. Уравнение Аррениуса.

11. Абсолютная скорость движения ионов. Числа переноса.

12. Вычислить числа переноса ионов H3O⁺, K⁺ и Cl^– для водных растворов HCl и KCl,

если при 25^°C l¥(H3О+) = 349,8; l¥(K+) = 73,5; l¥(Cl-) = 76,3 Ом^-1см²/моль.

13. Абсолютные скорости движения ионов при бесконечном разведении водного раствора и T = 298 K : UAg⁺= 6,42×10^-4 cм²· B^-1·с^-1 и UNO3- =7,4×10^-4 cм²· B^-1·с^-1. Вычислить эквивалентную (молярную) электропроводность бесконечно разбавленного водного раствора AgNO3.

14. Вычислить эквивалентную электропроводность l(CH3COONH4) раствора ацетата аммония при бесконечном разведении и 25^°C, если в тех же условиях эквивалентные электропроводности ионов Cl^- и Na⁺ и водных растворов хлорида аммония и ацетата натрия

имеют следующие значения: l¥(Cl-) = 76,3; l¥(Na+) = 50,1; l¥(NH4Cl) = 149,8; l¥(CH3COONa) = 91,0 Ом^-

¹см²моль^-1.

Лекция 7

ТЕРМОДИНАМИКА ПОВЕРХНОСТНЫХ ЯВЛЕНИЙ

7.1. Понятия поверхностных явлений

Поверхностные явления имеют место на границе раздела фаз. Реальная межфазовая граница – это поверхностный слой толщиной, не превышающий 1 нм, в пределах которого термодинамические параметры (концентрация компонентов, давление, температура и др.) испытывают резкие изменения. Причина возникновения поверхностных явлений – наличие избыточной поверхностной энергии на поверхности раздела фаз, т.к. молекулы вещества по обе стороны от границы имеют свободные, т.е. ненасыщенные валентности, они-то в совокупности и дают поверхностную энергию (dGS):

dGS = σ^ždSуд

где σ – поверхностное натяжение; dSуд –удельная поверхность.

Все системы, обладающие избыточной энергией – неустойчивы. Поэтому в дисперсных системах согласно 2 закону термодинамики самопроизвольно идут процессы с понижением dGS. Следовательно, поверхностную энергию можно снизить, уменьшив поверхностное натяжение или удельную поверхность. Поэтому все поверхностные явления тоже можно разделить на две группы:

1) поверхностные явления с уменьшением Sуд, при которых происходит самоукрупнение дисперсных частиц: а) коагуляция; б) коалесценция; в) образование сферических частиц.

2) поверхностные явления с уменьшением σ: адсорбция, адгезия, когезия, смачивание, растекание.

7.2. Адсорбция. Основные понятия. Классификация

Адсорбция – это накопление одного вещества на поверхности другого.

Адсорбент – это вещество, на поверхности которого идет накопление (1-ая фаза).

Адсорбтив (или адсорбат) – это то вещество, которое накапливается.

Адсорбция – это самопроизвольный процесс, т.е. энергетически выгодный.

Адсорбция относится к поверхностным явлениям.

В зависимости от агрегатного состояния адсорбента и адсорбтива различают следующие виды адсорбции:

· Адсорбция на границе жидкость / газ (воздух);

· Адсорбция на твердом адсорбенте: а) газов; б) жидкостей

В случае адсорбции на границе раздела жидкость – газ и адсорбции на гладких поверхностях величину адсорбции (Г) определяют относительно единицы площади границы раздела фаз:

Г = _S^п , моль / м²

· адсорбента.гдеn–количествоадсорбтива;S–площадь

Для твердого и особенно пористого порошкообразного адсорбента, имеющего значительную поверхность раздела фаз, адсорбцию выражают по отношению к единице массы адсорбента (т):

Г = _т^п , моль / кг

7.3. Адсорбция из газов на твердом адсорбенте

В качестве твердых адсорбентов используются: активированный уголь; силикагель (высушенный гель H2SiO3); окись Al2O3 (порошок); каолин; глинозем.

Механизм адсорбции: Адсорбция идет не на всей поверхности, а только на активных центрах (вершины, грани кристаллической решетки, трещины, выступы), т.к. на них атомы имеют ненасыщенные валентности.

Различают физическую и химическую адсорбции.

1) Особенности физической адсорбции.

^§ Осуществляется за счет слабых сил Ван-дер-Ваальса;

^§ Нелокализованная адсорбция, так как молекулы адсорбтива легко перемещаются от одного активного центра к другому;

^§ Обратимый процесс: адсорбированные молекулы газа удерживаются на активных центрах доли секунды, а затем отрываются (т.е. происходит десорбция). В момент равновесия скорость адсорбции равна скорости десорбции;

^§ Экзотермический процесс, поэтому с увеличением температуры усиливается десорбция молекул, а адсорбция снижается.

2) Особенности химической адсорбции.

^§ Осуществляется за счет образования прочных химических связей адсорбтива с адсорбентом;

^§ Локализованная адсорбция: молекулы прочно удерживаются на активном центре;

^§ Эндотермический процесс, поэтому с ростом температуры химическая адсорбция усиливается.

Однако нет четкой границы между физической и химической адсорбции. Обычно имеет место их сочетание.

Процесс адсорбции газов на твердом адсорбенте зависит от ряда факторов:

1. Адсорбция прямо пропорциональна площади адсорбента, т.е. чем больше площадь адсорбента, тем больше адсорбция;

2. Адсорбция зависит от природы адсорбента и адсорбтива, т.е. носит избирательный характер.

3. Адсорбция (Г) при постоянной температуре (Т = const) зависит от равновесного давления газа (Р). Эта зависимость выражается уравнением Фрейндлиха:

_Г ₌ _К _×_Р¹п_,

где K и n – эмпирические константы.

7.4. Адсорбция на твердой поверхности из растворов

Адсорбция из растворов имеет более сложный характер, чем из газов.

1) Растворимое вещество и растворитель являются конкурентами за активные центры адсорбента.

2) Скорость адсорбции из раствора меньше, чем скорость адсорбции из газов, так как скорость диффузии молекул в растворе меньше, чем в газах.

3) С повышением температуры адсорбция снижается (так как это физическая адсорбция).

4) Адсорбция из растворов может быть: а) молекулярная; б) ионная (если адсорбтив диссоциирует).

На адсорбцию из растворов влияют:

1) Природа адсорбента. Все твердые адсорбенты делятся на гидрофильные,

которые хорошо смачиваются водой (пористое стекло, силикагель (H2SiO4), глины (кильзегур, бентонтн), Al2O3), и гидрофобные, которые хорошо смачиваются неполярными органическими растворителями (уголь, графит, тальк). Гидрофильные адсорбенты нельзя использовать для адсорбции веществ растворимых в воде, так как возможно, что вода будет адсорбироваться лучше, т.е. вода является конкурентом за активные центры адсорбента. Их лучше использовать для адсорбции веществ из неводных растворов. Гидрофобные адсорбенты применяют при адсорбции веществ из водных растворов.

2) Природа растворителя. Чем лучше в данном растворителе растворяется адсорбтив, тем он хуже адсорбируется; чем хуже растворяется – тем лучше из него адсорбируется. Например, краситель фуксин на активированном угле хорошо адсорбируется из водного раствора и плохо из спиртового раствора.

3) Температура. С повышением температуры адсорбция уменьшается, так как это физическая адсорбция.

4) Время. Так как скорость адсорбции из растворов меньше адсорбции из газов, то времени необходимо больше.

7.5. Адсорбция электролитов

На твердом адсорбенте из раствора электролита адсорбируются преимущественно ионы одного вида. Это зависит от природы адсорбента или от природы ионов – их заряда, радиуса и степени гидратации. Чем больше заряд иона, тем лучше он адсорбируется. Из ионов с одинаковым зарядом лучше адсорбируется ион, имеющий наибольший радиус, так как он имеет наименьшую степень гидратации.

На поверхности кристаллического твердого тела из раствора адсорбируется тот из ионов, который входит в состав кристаллической решетки или может образовывать с одним из ионов решетки малорастворимое соединение (правило Фаянса-Пескова).

7.6. Обменная адсорбция

Обменная адсорбция представляет собой процесс обмена между раствором и твердой фазой – адсорбентом, точнее обмен ионов между двойным электрическим слоем адсорбента и средой. При этом твердая фаза поглощает из раствора ионы одного знака (катионы или анионы) и вместо них выделяет в раствор эквивалентное число других ионов того же знака.

Обменная адсорбция имеет ряд особенностей.

1). Обменная адсорбция специфична, т.е. для данного адсорбента к обмену способны только определенные ионы. Различают кислотные и основные адсорбенты, которые обмениваются с растворами катионами и анионами соответственно. Существуют также амфотерные адсорбенты, которые в одних условиях обменивают катионы, а в других – анионы.

2). Обменная адсорбция не всегда обратима.

3). Обменная адсорбция протекает более медленно, чем молекулярная адсорбция.

4). При обменной адсорбции может изменяться рН среды.

7.7. Теории адсорбции

Теория молекулярной адсорбции Ленгмюра.

1. Адсорбция является локализованной и вызывается силами, близкими к химическим.

2. Адсорбция молекул адсорбтива происходит на активных центрах.

3. На поверхности адсорбента может образовываться только один (мономолекулярный) слой адсорбтива.

4. Адсорбированные молекулы удерживаются на активном центре только в течение определенного промежутка времени.

5. Силы взаимодействия между адсорбированными молекулами не учитываются.

Ленгмюром было выведено уравнение изотермы:

где C – равновесная концентрация растворенного вещества; Г∞ - предельная адсорбция; k1, k2 – константы скорости прямой и обратной реакции.

Это уравнение применимо для адсорбции газов:

^Г⁼^Г¥ ^× _Р ₊^Р_К ^,

где Р – равновесное давление газа.

Изотерма Фрейндлиха.

Представления, развитые И.Ленгмюром, в значительной степени идеализируют и упрощают действительную картину адсорбции. На самом деле поверхность большинства адсорбентов неоднородна, между адсорбированными частицами имеет место взаимодействие, и адсорбция часто не ограничивается образованием мономолекулярного слоя. В этом случае изотерма адсорбции усложняется. Г.Фрейндлих предположил, что зависимость адсорбции от равновесной концентрации растворенного вещества (С) или равновесного давления газа (Р) носит экспоненциальный характер. Это выражается эмпирическим уравнением:

_Г₌ _К _×_С ¹п _,

_Г₌ _К _×_Р¹п_.

Теория полимолекулярной адсорбции М. Поляни (1915).

Эксперименты показали, что на самом деле адсорбция происходит более сложно (изотерма имеет S-образный вид). Эта кривая свидетельствует о том, что после насыщения активных центров (Г∞) адсорбция не заканчивается (кривая идет вверх), так как в результате взаимодействия адсорбированных молекул между собой и образуются 2-ой, 3-ий слои адсорбированных молекул, т.е. имеет место полимолекулярная адсорбция. М. Поляни предложил теорию полимолекулярной адсорбции. Основные положения теории:

1) Адсорбция обусловлена чисто физическими силами Ван-дер-Ваальса;

2) На поверхности нет активных центров, а адсорбционные силы действуют вблизи от поверхности адсорбента, образуя непрерывное силовое поле;

3) Размер силового поля больше чем размер молекулы адсорбируемых веществ;

4) Адсорбция носит полимолекулярный характер (наслаивается);

5) Адсорбционные силы не зависят от температуры.

Обобщенная теория С.Брунауэра, П.Эммета и Е Теллера (теория БЭТ).

Обе теории адсорбции (Ленгмюра и Поляни) не могут описать достаточно полно сложный процесс адсорбции.

Основные положения теории БЭТ.

1) На поверхности сорбента имеется определенное число активных центров, равноценных в энергетическом отношении;

2) Каждая молекула предыдущего слоя может притягивать молекулы 2-го слоя (следующего);

3) Адсорбированные молекулы в 1-ом и последних слоях не взаимодействуют.

Капиллярная конденсация.

При сорбции паров на твердых пористых адсорбентах адсорбционный процесс

может перейти в так называемую капиллярную конденсацию. Сначала пар адсорбируется на стенках пор (капилляров) сорбента, а затем конденсируется в жидкость. Далее слои этой жидкости соединяются, заполняя частично самые тонкие капилляры жидкостью, образующей вогнутый мениск. Давление насыщенного пара над вогнутым мениском всегда меньше давления пара над плоской поверхностью жидкости

и поэтому пар начинает конденсироваться над вогнутым мениском и капилляры полностью заполняются жидкостью. С увеличением равновесного давления капиллярная конденсация охватывает более крупные капилляры по сравнению с первичными капиллярами.

Вопросы для самоконтроля

1. Что такое адсорбция, адсорбент, адсорбтив? Примеры адсорбентов.

2. Адсорбция на границе "твердое тело - газ". Уравнение Фрейндлиха.

3. Физическая и химическая адсорбция их особенности. Десорбция.

4. Мономолекулярная теория адсорбции Ленгмюра, теория Поляни, БЭТ.

5. Адсорбция на границе "твердое тело - раствор": механизм, особенности, примеры. Виды изотерм. Факторы, влияющие на адсорбцию из растворов.

6. Адсорбция электролитов. Катиониты, аниониты. Механизм адсорбции электролитов.

7. Обменная адсорбция электролитов. Примеры, применение.

8. Из какой среды будет лучше всего извлекаться ацетон каолином: из воды, этилового спирта или бензола? Ответ поясните.

Лекция 8

ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ

8.1. Понятие поверхностного натяжения

На границе раздела двух любых фаз, например, жидкость/пар; твердое вещество/пар; две несмешивающиеся жидкости ж1/ж2, возникает поверхностное натяжение.

Рассмотрим поверхность раздела жидкость/воздух. Поведение молекулы на поверхности раздела и в объеме фазы сильно отличаются. В объеме фазы взаимодействие молекул уравновешено со всех сторон действием одинаковых молекул, поэтому Fравн.=0. В поверхностном слое Fравн.≠0, т.к. со стороны пара жидкости (dпара<dжидкости) действие слабее. Fравн. направлена перпендикулярно поверхности во внутрь жидкости и стремиться уменьшить S раздела. Поэтому поверхностному натяжению можно дать следующие определения:

· Поверхностное натяжение – это мера давления поверхностного слоя вещества на внутренние слои.

· Поверхностное натяжение – это сила (F), действующая на единицу длины периметра, ограничивающего межфазную поверхность и направленная по касательной к этой поверхности.

· Поверхностное натяжение – это работа по переносу молекул вещества из объема жидкости на поверхность раздела, т.е. работа создания единицы удельной поверхности

	Fs	é H ù
σ =		, _ê		ú	, если S=1, то σ = FS
	S уд		2
		ë м		û

Поверхностное натяжение жидкостей зависит от ряда факторов:

1) Химическая природа вещества. Чем сильнее межмолекулярные связи в данном веществе, тем больше σ, т.к. увеличивается работа по преодолению этих сил, для выведения молекул на поверхность. Установлено, что у неполярных жидкостей поверхностное натяжение меньше, чем у полярных.

2) Температура. С увеличением температуры силы сцепления молекул в поверхностном слое ослабевают и σ убывает. Существует Ткритич., когда σ = 0, т.к. исчезает граница раздела ж/пар

3) Давление. При увеличении давления пара над жидкостью поверхностное натяжение уменьшается.

4) Добавление веществ.

Вещества, снижающие поверхностное натяжение жидкости, называются поверхностно-активными веществами (ПАВ).

Вещества, повышающие поверхностное натяжение жидкости, называются поверхностно-инактивными веществами (ПИВ).

8.2. Поверхностно-активные вещества (ПАВ)

К ПАВ относятся органические вещества, имеющие дифильное строение молекулы: гидрофобную часть – углеводородный радикал R и гидрофильную часть – полярную, функциональную группу Х.

Вследствие дифильного строения молекулы ПАВ накапливаются на границе раздела фаз вода – воздух, ориентируясь при этом определенным образом. Гидрофильная часть молекул взаимодействует с водой, а неполярная гидрофобная часть выталкивается в неполярную фазу (воздух), т.е. имеет место адсорбция молекул ПАВ в поверхностном слое. При этом происходит самопроизвольное снижение поверхностной энергии за счет уменьшения поверхностного натяжения. Количественное соотношение между адсорбцией (Г) растворенных ПАВ, его концентрацией (С) в растворе и изменением поверхностного натяжения (σ) дает уравнение Гиббса:

Г = - _RT^C × ^D_D^s_C ,

где	Ds	=	^s 2			- s₁	- поверхностная активность вещества.
где	DС	=		С	2	- С	- поверхностная активность вещества.
					2	1

Для ПАВ ^D^s <0, т.к. с ростом концентрации σ – убывает.

DС

Для ПИВ а) ^D^s > 0 т.к. с увеличением концентрации σ – возрастает. Пример

DС

неорганические электролиты; б) ^D^s = 0, т.е. концентрация не влияет на σ, пример

DС

углеводы: глюкоза, фруктоза, крахмал.

Поверхностная активность	Ds	дифильных молекул ПАВ зависит от длины

	DС
	DС

углеводородного радикала (R), чем длиннее неполярный радикал, тем легче молекулы ПАВ вытесняют молекулы воды из поверхностного слоя, тем больше снижается поверхностное натяжение. Эта зависимость σ от длины радикала передается:

а) эмпирическим правилом Дюкло – Траубе: В любом гомологическом ряду ПАВ, удлинение углеводородного радикала на группу -СН2 увеличивает поверхностную активность в 3-3,5 раза. Это правило выполняется при комнатной температуре и низких концентрациях ПАВ.

б) эмпирическое уравнение Шишковского (для водных растворов ПАВ):

σ = σ о – В ln(1+КС)

где σ о – поверхностное натяжение воды; σ – поверхностное натяжение раствора; В – константа для данного гомологического ряда органических соединений.

ПАВ классифицируются на

1) Неионогенные ПАВ, которые не диссоциируют на ионы.

2) Ионогенные ПАВ, которые в растворах диссоциируют на ионы:

· анионные ПАВ (60% мирового производства) диссоциируют с образованием углеводородного аниона, носителя ПАВ – свойств. К ним относятся, в частности, мыла: С17Н35СООNa ↔ С17Н35СОО ^- + Na⁺

· Катионные ПАВ (≈10%) диссоциируют с образованием катиона, обладающего поверхностной активностью:

[C18H37NH3⁺]Cl^- ↔ C18H37NH3⁺ + Cl^-

· Амфотерные ПАВ (≈ %). Пример: белковые вещества, содержащие -NH2 и -СООН, в зависимости от pН среды проявляют свою поверхностную активность как катионные или анионные ПАВ.

8.3. Полуколлоиды

По своей природе ПАВ делятся на коллоидные и неколлоидные. Наибольшее значение имеют коллоидные ПАВ. К ним относятся: мыла, детергенты, дубильные вещества (танниды – производные галловой кислоты) и некоторые красители.

Коллоидные ПАВ часто называют полуколлоидами, т.к. для них характерны равновесные переходы: истинный раствор ↔ золь ↔ гель

Свойства растворов полуколлоидов сильно изменяются при переходе от очень низких концентраций к средним и высоким.

· При малых концентрациях ПАВ «хвосты» располагаются параллельно поверхности раствора и образуют тонкую пленку.

· При средних концентрациях усиливается взаимодействие углеводородных радикалов, что способствует их вертикальной ориентации.

· При высоких концентрациях ПАВ поверхностный слой раствора весь заполнен,

а остальные молекулы образуют агрегаты в виде мицеллы в объеме раствора, образуется: золь, с появлением мицелл вязкость раствора возрастает и золь переходит в гель, т.е. текучесть теряется.

Важнейшая характеристика растворов полуколлоидов – ККМ (критическая концентрация мицеллообразования)- это минимальная концентрация, при которой начинается мицеллообразование. ККМ выражается в процентах или кмоль/л (ККМ находится в интервале). В момент начала мицеллообразования меняются многие свойства раствора ПАВ (поверхностное натяжение, удельная электропроводность, показатель преломления).

8.4. Адгезия и когезия

Эти поверхностные явления часто сопровождают друг друга. При протекании этих процессов снижается поверхностное натяжение σ на границе двух фаз и снижается поверхностная энергия.

Эти явления широко распространены в природе и различных отраслях техники:

1. Склеивание различных материалов

2. Нанесение покрытий (лаки, краски, полимерных пленок)

3. При сварке и паянии металлов

4. Дубление, крашение и отделке кожи, меха. Адгезия и смачивание определяют качество изделий.

5. При упаковке продуктов питания: колбас, сыра, творога, кондитерских изделий Адгезия (или примыкание) – это процесс сцепления молекул (атомов, ионов)

различных фаз. Различают адгезию: а) между двумя различными жидкостями; б) между жидкостью и твердым телом и в) между двумя твердыми телами.

Когезия – это процесс сцепления молекул (атомов, ионов) внутри одной фазы. Например, имеется столбик однородной жидкости А. Если разделить его на два

столбика, т.е. возникли две новые поверхности жидкость А/пар с σА. Для этого совершили работу когезии АК, по преодолению сил сцепления между однородными молекулами: АК = 2 σА.

Рассмотрим второй пример: имеем столбик из двух несмешивающихся жидкостей: А(вода) и В(масло), в нем имеется поверхность раздела с межфазным поверхностным натяжением σАВ . Если столбик разрезать по границе раздела, то образуются два

столбика жидкостей А и В с поверхностным натяжением σА и σВ, при этом совершится работа адгезии: АА = σА + σВ – σАВ.

Согласно правилу Антонова: Межфазное поверхностное натяжение σАВ = σА – σВ т.е. межфазное поверхностное натяжение σАВ равно разности поверхностного натяжения двух жидкостей и тем больше, чем больше различаются по полярности жидкости А и В, а чем ниже значение тем выше взаимная растворимость жидкостей А и В.

Межфазное поверхностное натяжение σАВ зависит от температуры. С повышением температуры σАВ уменьшается, и существует такая критическая температура, при которой σАВ = 0 и жидкости неограниченно растворяются друг в друге.

8.5. Явление растекания

При нанесении на поверхность одной жидкости А нерастворимой в ней жидкости

В возможны два случая:

1. Жидкость В растекается по поверхности жидкости А с образованием тонкой пленки толщиной в одну молекулу.

2. Жидкость В не растекается и остается в виде капли.

При растекании жидкостей осуществляется работа адгезии (АА) и работа когезии (АК). Условие растекания выглядит следующим образом: α – коэффициент растекания, который равен: α = АА –АК.

Если α > 0, то АА > АК растекание происходит (случ. 1).

Если α < 0, то АА < АК жидкость В не растекается (случ. 2).

8.6. Явление смачивания

В данном случае рассматривается поверхностное натяжение на границе трех фаз (жидкость – газ – твердая поверхность)

При нанесении капли жидкости на твердую поверхность возможны два случая:

1. если АА > АК: адгезия (сила притяжения жидкость/твердая поверхность) больше чем когезия (силы притяжения молекул жидкости), то капля жидкости растекается по твердой поверхности, т.е. жидкость смачивает эту твердую поверхность.

2. если АА<АК, то жидкость не смачивает эту твердую поверхность.

От степени смачивания зависит форма капли жидкости:

· Если краевой угол смачивания θ < 90^º, то хорошее смачивание твердого тела;

· Если краевой угол смачивания θ > 90^º, то твердое тело плохо смачивается. По виду избирательного смачивания все твердые тела делятся на три основные

группы:

а) гидрофильные поверхности – хорошо смачиваются Н2О (стекло, кварц)

б) гидрофобные поверхности – не смачиваются Н2О (графит, сера)

в) абсолютно гидрофобные (парафин, тефлон, битум и др.)

Вопросы для самоконтроля

1. Поверхностное натяжение жидкостей и факторы, влияющие на него.

2. Поверхностно активные вещества ПАВ? Механизм их действия: определение, строение, примеры.

3. Классификация ПАВ. Примеры.

4. Адсорбция на границе "жидкость - газ". Изотерма Гиббса.

5. Чем определяется поверхностная активность ПАВ. Правило Траубе, уравнение Шишковского.

6. Что такое полуколлоиды? Почему их так называют? Что такое ККМ, как ее определить?

7. Процесс мицеллообразования в растворах ПАВ. Строение мицелл ПАВ.

8. Чем определяется поверхностная активность молекул карбоновых кислот и как она зависит от их строения?

9. Как построены мицеллы олеата натрия и какие происходят изменения в их строении с увеличением концентрации раствора мыла?

10. Число капель воды, вытекающей из сталагмометра, равно 39, моющего средства 70, поверхностное натяжение воды равно 72,7×10^-3 Н/м. Рассчитать поверхностное натяжение раствора моющего средства, если плотности обеих систем равны.

11. Когезия и адгезия. Что такое межфазное поверхностное натяжение? От чего оно зависит? Правило Антонова.

12. Условия растекания жидкости по поверхности.

13. Смачивание твердых поверхностей. Количественные характеристики смачивания.

14. Гидрофобные и гидрофильные поверхности.

15. Краевой угол воды на стекле равен 5^°, на полиэтилене 80^°, на сульфиде железа 70^°, на карбонате кальция 25^°. Расположите вещества в порядке уменьшения их гидрофильности. Ответ поясните.

Лекция 9

ДИСПЕРСНЫЕ СИСТЕМЫ

9.1. Дисперсные системы, их классификация

Дисперсными системами называются гетерогенные системы, в которых одно вещество в виде частиц различной величины распределено в однородной массе другого.

Дисперсная фаза – это раздробленное (диспергированное) на частицы вещество. Дисперсионная среда – это однородная среда, в которой распределены частицы

дисперсной фазы.

Состояние вещества в поверхностных слоях дисперсной фазы, обладающее избыточной поверхностной энергией, называют коллоидным состоянием.

Дисперсными системами является большинство окружающих нас реальных тел:

а) почва, глина, минералы и драгоценные камни в недрах Земли, мутная вода в водоемах, дым, пыль, облака, туман;

б) биологические ткани: кровь, плазма, лимфа, спинномозговая жидкость, кожа, волосы, мех, стекловидное тело глаза;

в) продукты питания: молоко и молочные продукты (сливки, сметана, сливочное масло, йогурт, сыр), тесто и изделия из него (сухари, печенье), кондитерские изделия, зефир, безе, шоколад, различные соусы и кремы, бульоны, паштеты, фарши;

г) многие лекарственные формы: порошки, мази, болтушки, аэрозоли (ингаляторы, вакцины от ожогов)

д) парфюмерные препараты в виде: аэрозоли, кремы, дезодоранты, губная помада, зубная паста, пудра, лаки;

е) стройматериалы: масляные краски, пенобетон, пеностекло, строительные растворы (бетонные, цементные, известковые и др.).

Дисперсные системы содержат частицы различной формы (сферической, цилиндрической, в виде параллепипеда), но чаще – неправильной геометрической формы. Размер частицы выражается через:

^üстепень дисперсности (а) – это минимальный размер частицы и выражается в м

(см);

^üдисперсность: D = [см^-1]; [м^-1];

^üудельная поверхность: , где S – площадь межфазной

поверхности; V – объем всех частиц.

От степени дисперсности зависит качество: а) многих пищевых продуктов: муки,

сахара, круп, шоколада; б) лекарственных форм: мази, пасты, порошки, взвеси.

Дисперсные системы классифицируются по 3-м признакам:

А) По степени дисперсности частиц дисперсной фазы

От размеров частиц дисперсной фазы зависят свойства дисперсных систем.

Таблица 9.1. Классификация дисперсных систем по степени дисперсности

частиц дисперсной фазы

Системы	Размер		Свойства дисперсных систем
	частицы, м

			Гетерогенные, неустойчивые; частицы быстро
ГДС (грубо-дисперсные			оседают;	непрозрачные		(рассеивают свет			в
	₁₀-7	– 10^-5	результате	отражения		и	преломления);		не
системы)
			фильтруются через бумажный фильтр; видны в

			обычный микроскоп
			Гетерогенные,		прозрачные;			относительно
			устойчивы (не оседают); интенсивно окрашены;
Коллоидные			опалесцируют (дают конус Тиндаля); фильтруются
	10^-9	– 10^-7	через бумажный		фильтр,	но	не	проходят через
растворы
			полупроницаемую мембрану; не видимы в

			обычный микроскоп, но обнаруживаются в
			ультрамикроскоп
			Гомогенные, прозрачные (оптически пустые);
Истинные	менее 10^-9		термодинамически устойчивые; фильтруются через
растворы			все фильтры (бумагу, пергамент); видны в

			электромикроскоп

Б) По агрегатному состоянию дисперсной фазы и дисперсионной среды Дисперсная фаза и дисперсионная среда могут быть в 3-х агрегатных состояниях:

газообразном (Г), жидком (Ж), твердом (Т). Поэтому различают 8 типов дисперсных систем (газ в газе – гомогенная система).

Табл. 9.2. Классификация дисперсных систем по агрегатному состоянию

Агрегатное				Дисперсионная среда
Агрегатное
состояние		Твердая		Жидкая		Газообразная
		Твердая		Жидкая		Газообразная

		металлические		суспензии	(холодное	аэрозоли: дым, пыль
		сплавы;	твердые	молоко);	коллоидные	(цементная, сахарная,
фаза	Твердая	коллоидные растворы;		растворы		мучная, космическая)
		драгоценные	камни;
		цветные стекла
Дисперсная		цветные стекла
		природные	минералы	эмульсии	(горячее	Аэрозоли: туман
	Жидкая	с	жидкими	молоко,	маргарин,	(облака, дезодоранты)
	Жидкая	включениями(опал,		майонез)
		включениями(опал,		майонез)
		жемчуг)
		Тверда	пена	Пены
	Газообразная	(пенопласт,	пемза,	(взбитые сливки)
		хлеб)

В) По характеру взаимодействия между частицами дисперсной фазы и дисперсионной сред

По интенсивности взаимодействия частиц между фазами на их поверхности раздела дисперсные системы делятся на лиофильные (сильное межмолекулярное взаимодействие) и лиофобные (слабое межмолекулярное взаимодействие).

Для лиофильных систем характерно активное взаимодействие между частицами дисперсной фазы и дисперсионной среды. Эти системы получаются самопроизвольно и обладают минимальной свободной поверхностной энергией, поэтому устойчивы без стабилизатора. Они гомогенные и равновесные. Частицы имеют объемную оболочку из молекул растворителя. К таким системам относятся растворы ВМС.

Для лиофобных систем характерно: частицы не имеют сродства к растворителю, т.е. почти полностью отсутствует взаимодействие между частицами дисперсной фазы и дисперсионной среды; частицы имеют только тонкую оболочку из молекул растворителя; такие частицы имеют большую избыточную свободную поверхностную энергию, поэтому склоны к самоукрупнению и выпадают в осадок. В качестве примера таких систем можно привести коллоидные растворы.

9.2. Получения дисперсных систем

Дисперсные системы могут быть созданы самой природой или получены искусственно в результате различных процессов. Все способы искусственного получения дисперсных систем можно разделить на две группы. Первая из них основана на диспергировании, т.е. на получении мелких частиц дисперсной фазы из сплошного и крупного по размерам тела; вторая, наоборот, связана с укрупнением частиц молекулярного размера до размеров частиц дисперсной фазы за счет конденсационных процессов.

Рассмотрим более подробно способы получения коллоидных растворов. Коллоидные растворы занимают по степени дисперсности промежуточное положение между истинными растворами и грубодисперсными системами. Поэтому они могут быть получены либо путем ассоциации (конденсации) молекул и ионов истинных растворов, либо раздроблением частиц грубодисперсных систем. Методы получения коллоидных растворов представлены двумя группами: методы конденсации и дисперсионные методы. В отдельную группу может быть выделен метод получения коллоидных растворов с помощью пептизации.

Основные условия получения коллоидных систем, независимо от применяемых методов, следующие:

1. нерастворимость вещества дисперсной фазы в дисперсионной среде;

2. достижение коллоидной дисперсности частиц (10^-9 – 10^-7 м);

3. наличие стабилизатора, который обеспечивает коллоидной системе агрегативную устойчивость (т.е. устойчивость к слипанию коллоидных частиц).

Метод диспергирования:

1. Механическое диспергирование. Осуществляется с помощью специальных коллоидных мельниц и дробилок различных типов.

2. Дробление ультразвуком. Колебания воздуха с большой частотой (10⁵…10⁶ Гц) называются ультразвуковыми волнами. Взвесь грубодисперсного вещества, подлежащего раздроблению, под действием ультразвуковых волн размельчается до коллоидного состояния.

3. Электрическое диспергирование. Метод основан на создании вольтовой дуги между электродами, сделанными из распыляемого металла, помещенными в охлажденную воду. При температуре вольтовой дуги металлы сначала испаряются, а затем пары конденсируются в холодной воде.

Методы конденсации

1. Методы физической конденсации:

А) Конденсация переохлажденных паров (образование тумана, дыма).

Б) Метод замены растворителя. Хороший растворитель для дисперсной фазы заменяют на плохой растворитель, но хорошо смешивающийся с хорошим растворителем. Т.е. из истинного раствора получают коллоидный раствор.

2. Методы химической конденсации. Коллоидные растворы можно получить в результате проведения химических реакций почти всех известных типов: реакции обмена, окислительно-восстановительных, гидролиза и др. Обязательное условие:

1. образование труднорастворимых веществ;

2. низкая концентрация реагирующих веществ;

3. избыток одного из реагентов, который выполняет роль стабилизатора коллоидной системы.

Метод пептизации (или дробление средой)

Суть метода: к свежеприготовленному рыхлому осадку прибавляют электролит (пептизатор), благодаря которому частицы осадка отделяются друг от друга и переходят в раствор. В отличие от других методов дробления в этом методе не происходит, т.к. частицы рыхлого осадка уже имеют коллоидный размер, а прибавленный пептизатор стабилизирует коллоидный раствор.

9.3. Строение мицеллы

Любая коллоидная система состоит из дисперсной фазы и дисперсионной среды. В гидрозолях дисперсионной средой является вода, а твердая дисперсная фаза распределяется в виде коллоидных частиц. Структурной единицей коллоидного раствора является мицелла.

Основную часть мицеллы составляет ядро. Оно состоит из большого числа атомов, ионов, молекул нерастворимого в воде вещества. Ядро имеет кристаллическое строение. Поверхность ядра обладает запасом свободной энергии и избирательно адсорбирует ионы их окружающей среды. Согласно экспериментально установленному правилу Пескова: на поверхности твердого вещества предпочтительно адсорбируются ионы, способные достраивать его кристаллическую решетку. Это ионы либо родственные, либо сходные по химической природе и форме.

В результате адсорбции ионов на ядре образуется положительно или отрицательно

заряженный агрегат. Ионы, создающие заряд агрегата, называются потенциалопределяющими. Заряженный агрегат электростатически притягивает к себе из раствора ионы с противоположным знаком – противоионы. Они располагаются в двух слоях: 1-й адсорбционный слой противоионов, который вплотную примыкает к агрегату и образует с ним гранулу (частицу), имеющую заряд по знаку совпадающий со знаком потенциалопределяющих ионов; 2-ой диффузный слой противоионов, ионы которого располагаются уже в растворе и удалены от гранулы.

Мицелла таким образом имеет двойной электрический слой (ДЭС), состоящий из

потенциалопределяющих ионов и противоионов. Суммарный заряд потенциалопределяющих ионов равен суммарному заряду противоионов, поэтому мицелла электронейтральна.

Схема мицеллы:

[{mAgI}nI^-^¯(n-x)K⁺]^-^¯xK⁺

↕ ядро ↨

↨ агрегат ↨

↨		гранула	↨
↨		мицелла		↨

9.4. Методы очистки дисперсных систем

Очистка дисперсной системы (коллоидного раствора или раствора ВМС) от содержащихся в них примесей в виде ионов или молекул осуществляется с помощью полупроницаемых мембран. Мембраны – это тонкие пористые пленки, пронизанные мельчайшими каналами, размер которых не превышает 10 нм. Этот метод называют диализом. Скорость диализа может быть от нескольких суток до нескольких месяцев.

Для более быстрой и полной очистки коллоидов от электролитов в производстве применяют так называемый электродиализ. Прибор, с помощью которого осуществляется электродиализ, называется электродиализатор. Иона проходят через полупроницаемые мембраны и притягиваются к электродам, с поверхности которых смываются водой. Продолжительность электродиализа сводится к нескольким часам и даже минутам. В общественном питании электродиализ получает всё большее распространение. Его широко используют для опреснения питьевой воды, обессоливания различных пищевых продуктов.

Ультрафильтрация основана на отделении дисперсной фазы от дисперсионной среды путем фильтрования коллоидных растворов через особые плотные пленки – ультрафильтры, способные задерживать коллоидные частицы. Для ускорения ультрафильтрацию проводят под давлением. Ультрафильтрацию широко используют для очистки воды, белков, нуклеиновых кислот, ферментов, витаминов.

Ультрацентрифугирование – осаждение коллоидных частиц в центрифугах с вакуумом (скорость оборотов центрифуги 60 тыс. об/мин). Этим методом можно осадить не только коллоидные частицы, но и макромолекулы белков; а также определить радиус коллоидных частиц и молекулярный вес ВМС (белков, нуклеиновых кислот, вирусов). Этим методом получают чистые вакцины (например, против гриппа), биопрепараты (g-глобулин), кровезаменители.

Вопросы для самоконтроля

1. Что называется дисперсной системой, фазой, средой? Примеры дисперсных систем.

2. Классификация дисперсных систем по степени дисперсности и агрегатному состоянию фазы и среды.

3. Способы получения дисперсных систем

4. Строение коллоидной частицы. Заряд гранулы и мицеллы. Правило Пескова. Условия образования коллоидных систем. Особенности коллоидного состояния.

5. Способы очистки дисперсных систем. Диализ, электродиализ, ультрафильтрация.

6. Как получить мицеллы с разным знаком заряда?

7. Составить схему строения мицеллы золя бромистого серебра, полученного при взаимодействии разбавленного раствора бромистого калия с избытком азотнокислого серебра.

Лекция 10

СВОЙСТВА ДИСПЕРСНЫХ СИСТЕМ

10.1. Механизмы образования и строения двойного электрического слоя (ДЭС)

Существуют следующие механизмы образования ДЭС: 1) Ионизация поверхности. Металл теряет электроны и заряжается положительно. 2) Избирательная адсорбция ионов. Поверхность адсорбирует ион более близкий по природе. 3) Образование двойного электрического слоя за счёт адсорбции на поверхности полярных молекул.

ДЭС состоит из ионов одного знака, относительно прочно связанных с дисперсной твёрдой фазой (потенциалопределяющие ионы), и эквивалентного количества противоположно заряженных ионов, находящихся в жидкой среде вблизи межфазной поверхности (противоионы).

При рассмотрении строения мицеллы было показано, что на поверхности лиофобных коллоидов ДЭС. Первая теория строения ДЭС была развита Гельмгольцем;

в его представлении ДЭС подобен плоскому конденсатору, внутренняя обкладка которого находится в твердой фазе, а внешняя – в жидкости параллельно поверхности ядра на расстоянии порядка диаметра иона. Потенциал электрического поля внутри ДЭС φ в этом случае линейно уменьшается с увеличением расстояния от поверхности.

Позднее Гуи и Чепмен предложили другую модель, согласно которой противоионы, благодаря тепловому движению, образуют вблизи твердой поверхности ядра диффузную ионную атмосферу. Уменьшение электрического потенциала ДЭС φ с увеличением расстояния r в этом случае происходит нелинейно.

Предложенная Штерном модель строении ДЭС объединяет ранние модели, учитывая как адсорбцию противоинов, так и их тепловое движение. Согласно этой модели, являющейся в настоящее время общепринятой, часть противоионов находится на расстоянии порядка диаметра иона от поверхности ядра, образуя так называемый слой Гельмгольца (адсорбционный слой противоионов), а другая часть образует диффузный слой (так называемый слой Гуи). Потенциал диффузной части ДЭС называется электрокинетическим потенциалом ξ (дзета-потенциалом).

10.2. Электрокинетические явления дисперсных систем

Электрокинетическими называют такие явления, которые возникают при воздействии электрического поля на дисперсные системы и в результате перемещения частиц дисперсной фазы или дисперсионной среды. Несмотря на различие электрокинетических явлений все они связаны с наличием ДЭС и определяются ξ-потенциалом.

Если поместить мицеллу в постоянное электрическое поле, то наблюдаются электрокинетические явления:

1) Электрофорез

Электрофорез - это перемещение под действием электрического поля частиц дисперсной фазы относительно дисперсионной среды.

Для вычисления скорости электрофореза (U) и дзета-потенциала (ξ) применяют уравнение Гельмгольца-Смолуховского:

U = ^x^E_l_h^ee_k ,

где E – напряжение прилагаемого электрического поля; l – расстояние между электродами; Е/l – напряженность электрического поля; η – вязкость среды; ε – относительная диэлектрическая проницаемость среды; εо = 8,85^ž10^-12 Ф/м - диэлектрическая постоянная вакуума; k =4π (для цилиндрических частиц), k =6π (для сферических частиц).

2) Электроосмос

Электроосмосом называют перемещение дисперсионной среды под действием внешнего электрического поля. Движение дисперсионной среды обусловлено притяжением разноименных зарядов.

3) Потенциал седиментации возникает при седиментации (оседании) частиц дисперсной фазы за счет избыточного заряда частиц, определяемого ξ-потенциалом. Частицы дисперсной фазы оседают под действием гравитации. Процесс оседания частиц называют седиментацией. При оседании частиц дисперсионная среда прак-тически остается неподвижной. Частицы движутся совместно с потенциалобразующим слоем ионов и адсорбционным слоем противоионов. Их перемещение относительно жидкой дисперсионной среды происходит по границе скольжения. Потенциал седиментации обратен электрофорезу.

4) Потенциал течения возникает при перемещении жидкой дисперсионной среды. Жидкость движется под влиянием внешнего воздействия: насоса, давления воздуха или какого-либо другого источника. При движении жидкости увлекаются противоионы диффузного слоя. В этом случае, как и в других электрокинетических явлениях, пе-ремещение жидкой дисперсионной среды относительно твердой дисперсной фазы происходит по границе скольжения и приводит к появлению разности потенциалов. Потенциал течения обратен электроосмосу.

10.3. Оптические свойства дисперсных систем

Оптические свойства дисперсных систем обусловлены взаимодействием электромагнитного излучения (света), обладающего определенной энергией, с частицами дисперсной фазы. Особенности оптических свойств дисперсных систем определяются природой частиц и их размерами, соотношением между длиной волны электромагнитного излучения и размерами частиц.

В коллоидных растворах размер дисперсных частиц (мицеллы) меньше ½ длины световой волны, поэтому для них характерно светорассеяние. В основе светорассеяния лежит явление дифракции - огибания коллоидных частиц световой волной. Волна огибает мицеллу, и она становится источником новых менее интенсивных волн, т.е. происходит как бы самосвечение каждой мицеллы. Явление рассеяния света мельчайшими частицами называется опалесценцией. Опалесценция наблюдается только “сбоку” и на темном фоне проявляется в мутноватости золя и переливах по окраске. Так белы золи (AgCl, серы, канифоли) смотрятся как голубоватые.

Чтобы наблюдать светорассеяние, пучок лучей, сконцентрированных с помощью собирательн.ых линз, пропускают через коллоидный раствор, помещенный в сосуд с плоскопараллельными стенками. Рассматривая этот раствор сбоку, можно видеть в нем светящуюся полосу в форме конуса (конус Тиндаля). Это явление получило название эффект Тиндаля.

Интенсивность свечения конуса, т.е. интенсивность светорассеяния, зависит от ряда факторов. Зависимость выражается формулой Рэлея, выражающей закон светорассеяния:

где Ip, Io – интенсивности рассеянного и падающего света; k – константа, зависящая от разности показателей преломления дисперсной фазы и дисперсионной среды; п - число частиц в единице объема, т.е. частичная концентрация золя; V - объем частицы дис-персной фазы; λ – длина волны падающего света.

Интенсивность рассеянного света пропорциональна частичной концентрации золя. На этом основано определение концентрации коллоидных растворов с помощью специальных приборов - ультрамикроскопов, нефелометров и др.

Когда свет проходит через какую-либо материальную среду, то он может не только рассеиваться, но и всегда в большей или меньшей степени поглощаться (абсорбироваться). Поглощение света зависит от индивидуальных химических свойств данного вещества, причем всякое вещество поглощает только определенную часть спектра, т. е. свет определенных длин волн. Зависимость между поглощающей способностью вещества, толщиной поглощающего слоя, интенсивностью падающего и прошедшего света выражается уравнением Бугера-Ламберта - Бэра:

I_пр = I e^-e^cd = I - I_пог ,

где Io и Iпр – соответственно интенсивности падающего и прошедшего светa; е - основание натуральных логарифмов; ε - коэффициент поглощения света; d - толщина слоя; с - молярная концентрация растворенного вещества. Для оценки соотношения интенсивности прошедшего и падающего света можно использовать следующее уравнение:

D = lg	I	= 0,43ecd.

	^Iпр

Величину D называют оптической плотностью или экстинкцией. Эта зависимость используется для определения концентрации раствора.

Большинство окрашенных истинных растворов, если в них не изменяется химическая структура молекул (в результате гидролиза, комплексообразования и др. причин) достаточно точно подчиняются этому закону. В коллоидных системах положение оказывается более сложным. В таких системах при измерениях должно учитываться не только поглощение, но и рассеяние света.

Окраска золей связана с избирательным поглощением световой волны определенной длины. Интенсивность окраски золей в десятки и сотни раз больше, чем

у истинных растворов (в частности, золи с металлическими частицами определенного размера обладают иногда чрезвычайно высокой интенсивностью окраски, превышающей в сотни раз интенсивность окраски некоторых красителей). Золи могут быть бесцветными или окрашенными, интенсивность окраски зависит от концентрации дисперсной фазы или размера частиц. Полихромия зависимость окраски золей одного и того же вещества от степени дисперсности.

Вопросы для самоконтроля

1. Механизм образования и строение двойного электрического слоя (ДЭС). Понятие электрокинетического потенциала.

2. Электрические свойства коллоидов: электрофорез, электроосмос, потенциал протекания

и оседания.

3. От чего зависит скорость электрофореза? Как измерить дзета-потенциал частиц? От чего зависит его величина?

4. В чем причина особых оптических свойств дисперсных систем?

5. Рассеивание света коллоидными растворами, опалесценция, закон Релея.

6. Какие методы исследования коллоидных растворов основаны на светорассеивании?

7. Сущность эффекта Тиндаля.

8. Поглощение света коллоидами, закон Бугера-Ламберта-Бера.

9. Чем определяется окраска коллоидов? Полихромия.

10. Вычислите дзета-потенциал частиц золя сульфида мышьяка, если при измерении электрофоретической скорости частиц приложенная внешняя ЭДС равна 240 В, расстояние между электродами 30 см, перемещение частиц за 10 мин 14,36 мм. Диэлектрическая проницаемость 81, вязкость 1,005×10^-3 Па×с. Форма частиц цилиндрическая.

Лекция 11

УСТОЙЧИВОСТЬ ДИСПЕРСНЫХ СИСТЕМ

Устойчивость означает способность дисперсных систем сохранять свой состав неизменным, когда концентрация дисперсной фазы и распределение частиц по размерам остаются постоянными во времени.

Различают два вида устойчивости: седиментационную и агрегативную.

11.1. Седиментация в дисперсных системах

Седиментационная (кинетическая) устойчивость определяется способностью противодействовать оседанию частиц. Седиментация, или оседание, приводит к разрушению дисперсной системы. На частицу дисперсной фазы действует гравитационная сила, которая вызывает оседание частиц. Противодействие этой силе зависит от размеров частиц. Для относительно крупных (ГДС) – это сила трения, для мелких (коллоидных и истинных растворов) – вызванная диффузией.

Седиментационное равновесие нарушается, и частицы начинают оседать (седиментировать), когда их размер превышает 100 нм. В условиях постоянной скорости оседания устанавливается равновесие между гравитационной силой и силой трения; оно позволяет определить размер частиц r в зависимости от скорости оседания (ν). Эта зависимость фиксируется формулой:


r =	9hn	,
r =	2(r - r )g	,

где η, ρ, ρₒ - вязкость среды, плотность частиц дисперсной фазы и дисперсионной среды.

11.2. Термодинамические и кинетические факторы агрегативной устойчивости

Под агрегативной устойчивостью подразумевают способность дисперсных систем противодействовать слипанию частиц. Взаимодействие и слипание твердых частиц приводит к образованию агрегатов. В результате происходит укрупнение частиц, структура дисперсной фазы претерпевает изменение, а образующиеся агрегаты способность оседать или всплывать. Агрегация и слипание твердых частиц называют

коагуляцией.

Взаимодействие жидких частиц дисперсной фазы приводит к образованию агрегатов, состоящих из капель. Затем при определенных условиях может происходить слияние капель. Этот процесс называют коалесценцией.

Агрегативная устойчивость дисперсных систем определяется соотношением сил притяжения, которые обусловлены межмолекулярными ван-дер-ваальсовыми силами,

и сил электростатического отталкивания. Современная физическая теория устойчивости коллоидных систем была развита Б. В. Дерягиным и Л. Д. Ландау (1937), Э. Фервеем и Я. Овербеком (1941). В соответствии с первыми буквами фамилий авторов теория носит название ДЛФО. В теории ДЛФО в качестве основного параметра, характеризующего стабильность коллоидной системы рассматривает расклинивающее давление – давление, которое необходимо приложить со стороны коллоидных частиц, чтобы толщина межфазной прослойки осталась неизменной.

К термодинамическим факторам агрегативной устойчивости можно отнести следующие:

· Электростатический фактор – возникновение ДЭС на поверхности частиц, препятствующего их взаимодействию;

· Адсорбционно-сольватный фактор – уменьшение межфазного натяжения при взаимодействии частиц дисперсной фазы со средой (благодаря адсорбции и сольватации);

К кинетическим факторам агрегативной устойчивости относятся следующие:

· Структурно-механический фактор обусловлен существованием на поверхности частиц различных пленок, обладающих упругостью и механической прочностью и препятствующих взаимодействию частиц (например, коллоидная защита);

· Гидродинамический фактор снижает скорость коагуляции благодаря повышению вязкости среды и изменению плотности частиц дисперсной фазы и дисперсионной среды.

11.3. Коагуляция коллоидных растворов

Коагуляция – процесс слипания коллоидных частиц с образованием более крупных агрегатов с потерей агрегативной и кинетической устойчивости.

Различают 2 стадии коагуляции:

^§скрытая коагуляция, когда невооруженным взглядом еще нельзя определить внешние изменения в золе.

^§явная коагуляция – легко обнаруживается визуально по следующим признакам: изменение цвета раствора; помутнение; выпадение осадка.

Чтобы вызвать коагуляцию нужно: нейтрализовать ДЭС (снизить ξ-потенциал, уменьшив диффузный слой противоионов); разрушить сольватную оболочку.

Это можно осуществить: прибавлением электролитов; нагреванием или замораживанием; механическим воздействием; высокочастотными колебаниями; ультрацентрифугированием; добавлением дегидратирующих веществ (спирта, ацетона, танина и др.).

Ряд закономерностей, установленных эмпирически, являются основой правил электролитной коагуляции.

1) Любые электролиты могут вызвать коагуляцию, но при достижении определенной концентрации в растворе.

Минимальная концентрация электролита, вызывающая явную коагуляцию называется порогом коагуляции (g)

_g₌ ^Сэл ^×^Vэл _, ^моль _.

^Vзоля^л

2) Правило Шульце-Гарди или правило значности.

· коагулирующим действием обладает не весь электролит, а лишь тот его ион, заряд которого противоположен заряду гранулы;

· чем выше валентность коагулирующего иона (z), тем сильнее происходит коагуляция:

g = ¹₆

· при одинаковой валентности иона коагулирющее действие возрастает с увеличением его радиуса.

3) В ряду органических ионов коагулирующее действие возрастает с повышением адсорбционной способности.

4) Влияние гидратации.

В ряду неорганических ионов с одинаковой валентностью, чем меньше гидратирован ион, тем больше его коагулирующее действие.

5) Коагуляция начинается при снижении значения ξ-потенциала до его критического значения (ξкр = 0,030 В).

Взаимная коагуляция золей. При взаимодействии золей с разноименными знаками зарядов частиц происходит коагуляция. Этот факт объясняли действием противоположных знаков зарядов частиц дисперсной фазы обоих золей. Таким образом, взаимную коагуляцию рассматривали как частный случай коагуляции электролитами, если один из золей принят в качестве электролита с большим ионом-коагулятором. Естественно, что при этом золи должны быть взяты в таком количественном соотношении, которое обеспечивало бы более или менее полную нейтрализацию заряда частиц.

Экспериментами было установлено, что взаимная коагуляция коллоидных систем может наблюдаться и тогда, когда частицы обоих золей несут электрический заряд одного и того же знака. В этом случае причиной потери устойчивости данной дисперсной системы в присутствии другой является адсорбция стабилизатора данной системы поверхностью другой системы и снижение вследствие этого концентрации стабилизатора в золе данной системы.

11.4. Механизмы электролитной коагуляции

Различают два механизма коагуляции коллоидных растворов электролитами – концентрационный и нейтрализационный.

Концентрационная коагуляция связана с увеличением концентрации электролита, не вступающего во взаимодействие с потенциалопределяющими ионами. При этом диффузный слой противоионов мицеллы сжимается, переходя в адсорбционный слой.

В результате уменьшается электрокинетический ξ-потенциал и по достижение его критического значения начинается коагуляция. Термодинамический φ потенциал при этом не меняется.

При нейтрализационной коагуляции ионы прибавляемого электролита нейтрализуют потенциалопределяющие ионы, уменьшается термодинамический φ потенциал и соответственно уменьшается дзета-потенциал. При достижении последнего критического значения начинается коагуляция.

11.5. Коллоидная защита

Коллоидная защита – это повышение устойчивости лиофобных золей по отношению к электролитам. Она достигается путем добавления к золям ВМС: белки (желатина, яичный белок, альбумин, казеин); полисахариды (крахмал, декотрины); некоторые ПАВ (стеарат и олеат натрия); салонины и др.

Механизм защитного действия можно объяснить тем, что макромолекулы ВМС

адсорбируются на поверхности коллоидных частиц, создавая адсорбционные сольватные слои, которые повышают гидрофильность коллоидных частиц. Вследствие

этого усиливается взаимодействие частица – растворитель. Сольватные слои обеспечивают большое расклинивающее давление при сближении двух частиц и препятствуют их слипанию. Защитное действие усиливается, если в адсорбционном слое ВМС образуются гелеобразные структуры, обладающие повышенной прочностью и упругостью (это относится, например, к желатине).

Для количественной характеристики защитного действия различных ВМС Р.

Зигмонди предложил термин “ЗОЛОТОЕ ЧИСЛО”.

“ЗОЛОТОЕ ЧИСЛО” – такое количество мг защитного вещества (ВМС), которое необходимо добавить, чтобы предотвратить изменение цвета 10 мл красного золя золота в фиолетовый при добавлении 1 мл 10 % раствора NaCl.

Чем меньше золотое число, тем сильнее защитное действие высокомолекулярного вещества. Различные ВМС обладают различным золотым числом.

Вопросы для самоконтроля

1. Седиментационная и агрегативная устойчивость колодных растворов.

2. Теория ДФЛО. Что такое расклинивающее давление, его составляющие?

3. Термодинамические и кинетические факторы агрегативной устойчивости.

4. Коагуляция коллоидных растворов, определение, стадии, ее причины?

5. Правила электролитной коагуляции.

6. Какие ионы могут вызывать коагуляцию? Правило Шульце-Гарди.

7. Что такое порог коагуляции и как его определить?

8. Механизмы электролитной коагуляции (нейтрализационный и концентрационный).

9. Что такое взаимная коагуляция?

10. Защита коллоидов от коагуляции. «Золотое число».

11. В три колбы налито по 100 мл золя гидроксида железа. Чтобы вызвать явную коагуляцию золя, потребовалось в первую колбу прибавить 10,5мл 1М хлорида калия, во вторую - 62,5мл 0,02 М сульфата натрия и в третью-37,0 мл 0,003 М фосфата натрия. Вычислите пороги коагуляции и определите знак заряда частиц золя.

12. Золь гидроксида железа, полученный неполным гидролизом хлорного железа, коагулируют сульфатом натрия, хлоридом натрия и хлоридом бария. Какой из электролитов окажет наиболее сильное коагулирующее действие? Объясните.

Лекция 12

МИКРОГЕТЕРОГЕННЫЕ СИСТЕМЫ

12.1. Золи и суспензии

Золи и суспензии, а также их производные – гели, пасты – являются разновидностями одного и того же типа дисперсных систем Т/Ж, которые различаются размерами и концентрацией дисперсной фазы. Золи или коллоидные растворы были рассмотрены раньше (лекция 8).

Суспензии – это дисперсные системы с твердой дисперсной фазой и жидкой дисперсионной средой.

В зависимости от концентрации дисперсной фазы суспензии делятся на: ^ü Разбавленные (до 25 %)

^ü Концентрированные (свыше 25 %), которые также называются пастами. Суспензии получают аналогично коллоидным растворам.

1) Метод диспергирования. Твердые вещества измельчают в порошки с размером частиц 10^-7 - 10^-5 м, а затем взмучивают в дисперсионной среде.

2) Методы конденсации.

a) Физическая конденсация: переохлаждение расплава или выделение из пересыщенного раствора.

b) Химическая конденсация: реакции разложения (AgCl, CaSO4, BaSO4).

c) Коагуляция коллоидных частиц.

Суспензии агрегативно и кинетически неустойчивые системы, поэтому необходимы стабилизаторы. В качестве последних используют:

1) ЭЛЕКТРОЛИТЫ. Механизм стабилизации следующий: ионы электролита избирательно адсорбируются вокруг твердой частицы (согласно правилу Пескова). В результате возникает ДЭС с ξ-потенциалом. Агрегативная устойчивость возникает за счет электростатического отталкивания.

2) ПОВЕРХНОСТНО-АКТИВНЫЕ ВЕЩЕСТВА (ПАВ) И ВЫСОКОМОЛЕКУЛЯРНЫЕ СОЕДИНЕНИЯ (ВМС).

Если частицы суспензии смачиваются дисперсионной средой, то агрегативная устойчивость возрастает. Возможна природная смачиваемость. Например, CaCO3, CaSO4, Na2SiO3 (песок) смачиваются водой, а активированный уголь – бензином.

Смачиваемость можно придать с помощью ПАВ. Молекулы ПАВ адсорбируются на частице сажи неполярным углеводородным радикалом, а полярная группа ориентирована к воде и сообщает смачиваемость частице.

Молекулы ВМС вокруг частицы сажи образует механическую защитную оболочку. Полярные группы ВМС притягивают полярные молекулы воды.

12.2. Эмульсии

Эмульсия – это дисперсная система, состоящая из двух взаимно нерастворимых жидостей, одна из которых в виде капелек диспергирована в другой. Размер капли 10^-7

– 10^-5 м. ПРИМЕРЫ: теплое молоко, сливочное масло, маргарин, мясной бульон. Способы получения:

1. Диспергирование.

a) Самопроизвольное (если одну жидкость вливают с определенной скоростью в другую);

b) С помощью мешалок различных конструкций;

c) Гомогенизация (вторичное диспергирование через фильтры под давлением). Эмульсии классифицируются:

· В зависимости от природы образующих жидкостей делятся на:

- Эмульсии масла в воде (М/В) или эмульсии I рода (прямые).

- Эмульсии воды в масле (В/М) или эмульсии II рода (обратные).

· В зависимости от концентрации дисперсной фазы:

- Разбавленные (содержание дисперсной фазы не больше 0,1 % объема). Диаметр частицы приблизительно равен диаметру мицеллы, образуются самопроизвольно, форма сферическая.

- Концентрированные (содержание дисперсной фазы не более 74 % объема). Сохраняется сферическая форма капли.

- Высококонцентрированные (содержание дисперсной фазы больше 74 %). Капли сдавливают друг друга. Имеют форму многогранника, разделенного тонкой пленкой, т.е образуются “соты”. Вязкость большая.

Эмульсии термодинамически неустойчивые системы. Самопроизвольное слияние капелек дисперсной фазы – коалесценция. Этот процесс приводит к разрушению эмульсии и разделению на две жидкости. Для получения устойчивой эмульсии нужны стабилизаторы – эмульгаторы.

В качестве эмульгаторов применяются вещества 2 типов:

a) Жидкие вещества: ПАВ и ВМС (по аналогии с суспензиями).

Поверхностная активность определяется соотношением между гидрофильной и гидрофобной частями молекул ПАВ. Уравновешивание гидрофильного и лиофильного взаимодействий, так называемый гидрофильно-липофильный баланс (ГЛБ), т.е. определенное оптимальное соотношение действия воды и масла на молекулы ПАВ, определяет условие образования адсорбционного слоя на границе раздела двух жидкостей. ГЛБ является эмпирической безразмерной величиной и является отношением сродства неполярных групп молекул ПАВ к углеводородной жидкости и сродства полярной группы молекулы ПАВ к воде. Число ГЛБ – есть отношение работы адсорбции молекул ПАВ на границе М/В из фазы масло к работе адсорбции из водной фазы. Максимальная эмульгирующая способность зависит от свойств полярной гидрофильной части молекулы ПАВ и для мыла она реализуется, когда групповое число составляет 12-18.

b) Твердые эмульгаторы (порошки). Гидрофильные эмульгаторы, которые хорошо смачиваются водой (глина, мел, гипс), стабилизируют эмульсии I рода (М/В). Гидрофобные эмульгаторы (уголь, сажа) стабилизируют эмульсии II рода (В/М).

Обращение фаз или инверсия – это взаимное превращение эмульсии 2-х типов:

Эмульсия I рода (М/В) ⇆ Эмульсия II рода (В/М)

Инверсию можно вызвать:

a) Введение эмульгатора, стабилизирующего обратный тип эмульсии.

Например, эмульсию 1 рода стабилизирует гидрофильный эмульгатор (олеат натрия – С17Н35СООNa). Добавляя гидрофобный эмульгатор (олеат Ca, Cr, Mg, Fe, Al) можно перевести эмульсию 1 рода в эмульсию 2 рода.

b) Введение добавок, которые в результате химической реакции превращают эмульгатор данного типа эмульсии в эмульгатор для обратного типа эмульсии.

2 RCOONa + CaCl2 → (RCOO)2Ca + 2 NaCl

(RCOO)2Ca (кальциевое мыло) – гидрофобный стабилизатор эмульсии 2 рода.

c) Обращение эмульсии может быть вызвано длительным механическим воздействием.

d) Обращение фаз эмульсии при достижении определенной концентрации дисперсной фазы.

12.3. Пены

Пены – грубодисперсные системы, в которых дисперсная фаза – газ, а дисперсионная среда – жидкость или твердое вещество.

Пены бывают:

a) Низкоконцентрированные или разбавленные (когда пузырьки газа находятся на большом расстоянии друг от друга. Пузырьки газа имеют сферическую форму с радиусом 0,1 мм до 1 см. Пример, газированная вода, пиво, шипучие вина. Такие системы - короткоживущие вследствие неустойчивости.

b) Высококонцентрированные. Типичные пены. Они имеют ячеистую сотообразную структуру. Газовые пузырьки сдавливают друг друга, поэтому форма пузырька – многоугольник, отделенный тонкой пленкой жидкости.

Получение пен осуществляется двумя способами:

1) Диспергирование.

^Øдиспергированием газа (воздуха) при встряхивании сосуда, частично заполненного жидкостью, или интенсивным перемешиванием вращающимися мешалками;

^Øпропусканием газа через пористую перегородку в слой жидкости (барботирование);

2) Химическая конденсация.

^Øвыделением газа или пара в виде новой дисперсной фазы при кипении жидкости или из пересыщенного раствора, например в результате химической реакции, при которой выделяется газ:

NаНСОз + HCl = NaCI + Н2О + СО2.

^ØРеакция брожения (например, при образовании шампанского, пива).

Пены характеризуются следующими показателями:

1) Кратность пены, которая равна отношению объёма пены к объёму жидкости;

2) Дисперсность, которая равна среднему размеру пузырьков и средней толщине пленок жидкости;

3) Устойчивость пены характеризуется временем ее существования - временем самопроизвольного разрушения столба пены до половины его начальной высоты или объема.

Пены неустойчивые термодинамические системы. Со временем пленки жидкости стекают с пузырька под действием силы тяжести и пузырьки объединяются. Происходит расслоение системы: жидкость внизу, а газовая фаза сверху.

Устойчивую пену можно получить в присутствии пенообразователей

(стабилизаторов). Устойчивость зависит от природы и концентрации пенообразователей.

К пенообразователям относятся:

a) ПАВ (спирты, жирные карбоновые кислоты, их натриевые и калиевые соли – мыла). Максимальная устойчивость достигается при средней длине углеводородного радикала и средней концентрации пенообразователя. Пенообразователь адсорбируется

на межфазной поверхности. При этом углеводородный радикал обращен в газ, а полярная часть в воду. Пенообразователь снижает поверхностное натяжение жидкости. Ионогенные ПАВ создают ДЭС и делают более прочным каркас из жидкости.

b) ВМС, которые повышают вязкость жидкости, что позволяет пленке жидкости дольше удерживаться на пузырьке

На устойчивость пены также влияют:

1. Температура. Повышение температуры обычно снижает устойчивость пены, так как происходит десорбция пенообразователя с межфазной поверхности и понижается вязкость, а также ускоряется испарение дисперсионной среды (пленка обезвоживается).

2. Вязкость дисперсионной среды. Чем больше вязкость, тем выше устойчивость.

3. Введение в дисперсионную среду электролитов. Это вызывает как бы коагуляцию, и пена расслаивается.

4. рН среды.

12.4. Аэрозоли

Аэрозоли – грубодисперсные системы, у которых дисперсная фаза – частички твердого или жидкого вещества, а дисперсионная среда – газ.

Различают простые и сложные аэрозоли. Простые делятся на: пыль, дым (Т/Г) и

туман (Ж/Г). Сложные: смог (Т/Г + Ж/Г).

Форма частиц аэрозоля зависит от агрегатного состояния дисперсной фазы. В туманах капли жидкости имеют шарообразную форму, а у пыли форма частицы различна.

Аэрозоли образуются:

1) Методами конденсации.

^Ø Физическая конденсация. При понижении температуры происходит конденсация паров. Например, при конденсации паров атмосферы образуются облака, состоящие из водяных капель и кристалликов льда.

^ØХимическая конденсация. HCl + NH3 → NH4Cl – белый дым.

2) Методами диспергирования.

Твердое или жидкое вещество измельчают механическим путем, а затем распыляют

в газовой фазе с помощью форсунок, пульвизаторов, газовых баллончиков. (парфюмерия, краски, лаки, инсектициды и др.).

Аэрозоли по свойствам близки к коллоидным растворам.

1) Частички аэрозоля имеют ДЭС, который препятствует их слипанию в крупные агрегаты. Электрический заряд у частиц аэрозоля возникает за счет:

^§ Механического трения частиц друг о друга;

^§ Под действием лучей различного происхождения; ^§ Адсорбции ионов из газов.

2) Частицы аэрозоля по размеру близки к мицеллам, способны рассеивать и поглощать свет. Поэтому аэрозоли имеют голубые оттенки (например, дым сигарет). Однако для некоторых аэрозолей имеет место большая разница в показателях преломлениях газовой дисперсионной среды и жидкой или твердой фазы, поэтому рассеяние у них более интенсивно, и они не пропускают свет.

Вопросы для самоконтроля

1. Что такое суспензии? Классификация и примеры суспензий.

2. Способы получения устойчивых суспензий. Примеры стабилизаторов.

3. Эмульсии: определение, классификация, примеры.

4. Типы эмульсий. Как получить эмульсию первого и второго типа? Гомогенизация.

5. Типы эмульгаторов, механизм стабилизации эмульсий.

6. Обращение фаз у эмульсий?

7. Свойства различных эмульгаторов, коэффициент ГЛБ.

8. Характеристика пены: получение, строение, примеры.

9. Стабилизаторы (пенообразователи) различных пен. Количественные характеристики пены (кратность, устойчивость, вязкость).

10. Аэрозоли: определение, классификация, получение, примеры, применение.

11. Даны порошки, состоящие из частиц крахмала, муки, полиэтилена и графита. Объясните, какие из этих порошков могут образовывать агрегативно устойчивые суспензии в воде и бензине.

12. Какого типа образуется эмульсия из воды и оливкового масла при использовании в качестве эмульгатора яичного белка?

Лекция 13

РАСТВОРЫ ВЫСОКОМОЛЕКУЛЯРНЫХ СОЕДИНЕНИЙ (ВМС)

13.1. Определение, классификация ВМС

Высокомолекулярные соединения (ВМС) – это соединения с молекулярной массой, начиная 5^ž10³ - 5^ž10⁶ и выше. Молекула ВМС состоит из многократно повторяющихся участков (элементарных звеньев) и называется макромолекулой.

1) По своему происхождению ВМС разделяются на:

· Природные: биополимеры, растительные и животные белки, нуклеиновые кислоты.

· Искусственные, которые получают химической обработкой природных ВМС: ацетатный шелк и другие сложные эфиры целлюлозы; нитроцеллюлоза.

· Синтетические, которые получают по реакции поликонденсации или полимеризации из низкомолекулярных соединений: полиэтилен, капрон, полистирол нитрон.

2) По строению макромолекулы ВМС бывают:

· Линейные (длина макромолекулы много больше ее диаметра). Длинные гибкие макромолекулы могут закручиваться в спираль (например, у белков),которые при определенных условиях могут принять форму клубка (глобула) за счет водородных связей.

· Разветвленные.

· Сетчатые. Имеют структуру в виде сетки, т.к. линейные макромолекулы могут образовывать поперечные межмолекулярные связи (мостиковые связи).

13.2. Особенности растворов ВМС

ВМС образуют растворы, которые по некоторым свойствам близки к золям:

1. Близкие значения размеров макромолекул и мицелл, и по форме они близки, так как макромолекулы (в частности белков) закручиваются в глобулу.

2. Макромолекулы не проходят через полупроницаемую мембрану, т.е. имеет место диализ.

3. Сходные молекулярно-кинетические свойства:

· Наличие броуновского движения;

· Медленная диффузия, как у золей;

· Низкое осмотическое давление.

4. Близкие электрические (электрофорез, электроосмос) и оптические (рассеяние, поглощение) свойства.

5. Могут коагулировать.

Растворы ВМС в отличие от коллоидных растворов характеризуются следующими особенностями:

1. Структурной единицей раствора ВМС является макромолекула, имеющая дисперсность коллоидных растворов 10^-9 ¸ 10^-7 м. Мицелла состоит из тысяч и миллионов молекул низкомолекулярного вещества.

2. Процесс растворения ВМС протекает самопроизвольно, осуществляемый с уменьшением свободной энергии (ΔG < 0), поэтому растворы ВМС – термодинамически устойчивые системы. Коллоидные растворы получают

специальными методами (диспергирования и конденсации), затрачивая при этом механическую, химическую и электрическую энергию, и представляют собой гетерогенные термодинамически неустойчивые системы.

3. Растворы ВМС образуются и существуют долгое время и при высоких концентрациях без стабилизатора.

4. Для растворов ВМС характерна аномально высокая вязкость. Вязкость коллоидных растворов равна вязкости дисперсионной среды (в частности, воды).

5. Макромолекулы ВМС сильно сольватированы.

6. ВМС способны образовывать не только истинные растворы, но и типичные лиофобные золи, если в качестве дисперсионной среды использовать такую жидкость, по отношению к которой данное ВМС является лиофобным, т.е. не способным раствориться в ней.

7. Сильное межмолекулярное взаимодействие характерно для растворов ВМС.

13.3. Электрические свойства растворов ВМС

Электрические свойства растворов ВМС обусловлены наличием поверхностного электрического заряда.

1. Заряд у макромолекулы может быть собственный, обусловленный наличием ионногенных групп, которые в водных растворах способные диссоциировать. В зависимости от природы ионногенных групп различают: полимерные кислоты, которые содержат кислотные группы; полимерные основания (имеется амино-группа –NH2); полиамфолиты, содержащие одновременно и кислотные, и основные группы.

2. Макромолекулы могут адсорбировать на своей поверхности заряды из раствора.

3. При отсутствии ионногенных групп электрический заряд может возникнуть благодаря неравномерному распределению электронов.

Доказать наличие электрического заряда у макромолекулы ВМС можно с помощью электрофореза.

Белки являются важнейшими биополимерами, построенные из остатков α-аминокислот, соединенных между собой пептидными связями. Аминокислоты являются амфотерными электролитами, т.к. содержат кислотную группу –СООН и основную –NH2.

NH2-R-COOH ⇄ ⁺NH3-R-COO ̅

По химическим свойствам белки могут быть кислыми, основными и нейтральными.

Заряд макромолекулы белка зависит от:

· Соотношения кислотных и основных групп. В кислых белках преобладают группы –СООН, поэтому в нейтральной среде макромолекула заряжена отрицательно. Нейтральные белки в нейтральной среде не имеют электрического заряда.

· Кислотности (рН) среды. Изменяя рН среды можно изменять и поверхностный заряд макромолекулы.

Такое состояние, когда молекулы белка в растворе электронейтральны,

называется изоэлектрическим состоянием (ИЭС).

Значение рН, при котором макромолекула белка, находится в изоэлектрическом состоянии, т.е. не имеет электрического заряда, называется изоэлектрической точкой (ИЭТ).

Каждый белок имеет свою ИЭТ. У кислых белков ИЭТ < 7; у основных – ИЭТ >7; нейтральные белки имеют ИЭТ = 7.

В ИЭТ (линейная макромолекула белка закручивается в глобулу) свойства растворов белков резко меняются:

· минимальная растворимость; · минимальная гидратация; · минимальная вязкость;

· минимальное осмотическое давление; · минимальная степень набухания; · минимальная электропроводность. ИЭТ определяется:

1. Прямым методом. Определяют рН раствора, при котором скорость электрофореза равна нулю.

2. Косвенным методом. Измеряют вязкость растворов ВМС с разным значением рН. В ИЭТ вязкость минимальна.

13.4. Молекулярно-кинетические свойства растворов ВМС

Для растворов ВМС характерна диффузия. Так как макромолекулы имеют большие размеры, то они не проходят через полупроницаемую мембрану, поэтому характерен диализ.

Для растворов ВМС осмотическое давление значительно выше, чем следует из закона Вант-Гоффа (π = СRT), т.к. макромолекула благодаря большим размерам и гибкости ведет себя в растворе как несколько более мелких молекул.

13.5. Оптические свойства растворов ВМС

Для растворов ВМС так же как и для лиофобных золей характерно светорассеяние и поглощение.

Светорассеяние у растворов ВМС проявляется, но величина рассеяния для них не так велика.

Окраска растворов ВМС зависит от избирательного поглощения света. Максимум этого поглощения расположен вне видимой области спектра, поэтому растворы ВМС в видимых лучах бесцветны. Растворы ВМС могут обладать сильным поглощением в ультрафиолетовой и инфракрасной областях.

13.6. Растворение ВМС. Набухание

Процесс поглощения ВМС больших объемов низкомолекулярной жидкости, сопровождающейся значительным увеличением объема ВМС, называется набуханием.

Процесс проникновения молекул растворителя в макромолекулы ВМС приводит к тому, что при набухании объем полимера всегда увеличивается, а объем всей системы уменьшается. Уменьшение объема системы при набухании, называемая контракцией.

При набухании происходит диффузия молекул растворителя в высокомолекулярное вещество.Это обусловлено двумя факторами: (достаточно большими промежутками между макромолекулами ВМС; большей подвижностью маленьких, по сравнению с макромолекулами ВМС, молекул растворителя).

Процесс растворения ВМС можно разделить на четыре стадии:

1. Начальная стадия. Система гетерогенна и двухфазна. Представляет собой чистую низкомолекулярную жидкость и чистый полимер.

2. Стадия набухания. На этой стадии система расслаивается на две фазы. Одна фаза

– набухший полимер. Вторая фаза - чистая низкомолекулярная жидкость.

3. Система двухфазная. Набухший полимер, в котором расстояние между макромолекулами настолько увеличились, что они начинают переходить в низкомолекулярную жидкость, образуя разбавленный раствор ВМС.

4. Стадия полного растворения – превращение гетерогенной (двухфазной) системы в гомогенную.

Существуют ограниченное и неограниченное виды набухания. Ограниченное – набухание не переходит со временем в полное растворение, а останавливается на второй или третьей стадии. Примером может служить набухание при комнатной температуре желатина.

Неограниченное набухание представляет непрерывный процесс, переходящий через все четыре стадии и заканчивающийся полным растворением. Образуется однофазная система. Например, так набухают каучуки в бензоле, нитроцеллюлоза в ацетоне, белок в воде, целлюлоза в ацетоне.

Процесс набухания носит избирательный характер. Полярные полимеры набухают в полярных растворителях. Неполярные ВМС – в неполярных жидкостях.

Скорость набухания полимера возрастает: с повышением температуры, при более высокой степени измельченности полимера, у свежего (молодого) полимера.

Количественно процесс набухания определяется степенью набухания (α):

_a₌^m ^-^m _, m

где тₒ, т - масса полимера до и после набухания.

Процесс набухания характеризуется увеличением объема набухшего тела. Если создать препятствие увеличению объема набухающего тела, то при этом развивается давление, называемое давлением набухания.

Теплота набухания – это теплота, выделяемая в процессе набухания (экзотермический процесс).

13.7. Вязкость растворов ВМС

Вязкость жидкости – это сопротивление (или сила трения), возникающее при перемещении одного слоя жидкости относительно другого.

По характеру вязкого течения жидкостные дисперсные системы делятся на две группы:

1) бесструктурные системы, частицы которых более или менее свободны и почти не взаимодействуют друг с другом (растворы низкомолекулярных веществ, разбавленные эмульсии, суспензии и золи);

2) структурированные системы — содержат частицы, взаимодействующие друг с другом и с дисперсионной средой (растворы ВМС, концентрированные эмульсии и суспензии).

Системы первой группы подчиняются закону Ньютона:

f =hS ^d_dyⁿ ,

где f – сила сопротивления течению между слоями; S – площадь слоев жидкости; η – вязкость; dν = ν2 – ν1 – различие в скоростях двух слоев жидкости; dy = y2 – y1 - расстояние между слоями;

и закону Пуазейля:

h = ^p^r ⁴ DPt, 8Vl

где V – объем жидкости, вытекающей из трубки; r и l – радиус и длина трубки; Р – разность давления на концах трубки; τ – время истечения жидкости.

Количество жидкости, протекающей через капилляр в единицу времени, изменяется прямо пропорционально давлению, а коэффициент вязкости является величиной постоянной и не зависит от градиента скорости или давления, приложенного к капиллярному вискозиметру.

Структурированные системы не подчиняются законам Пуазейля и Ньютона. Вычисленная по соответствующему уравнению вязкость таких систем имеет переменное значение и является функцией градиента скорости. У таких систем чем выше давление, под которым происходит истечение жидкости по капилляру, тем больше скорость истечения, т. е. тем ниже величина вязкости, найденная опытным путем. При рассмотрении поведения структурированных систем речь идет

о кажущейся, или эффективной вязкости nкаж, так как истинная вязкость жидкости от скорости истечения не зависит. Аномальное вязкое течение жидких систем второй группы обусловлено возникновением в их объеме внутренних структур.

Наиболее благоприятные условия для образования таких структур наблюдается в растворах ВМС, так как в большинстве случаев макромолекулы ВМС имеют линейное строение, причем длина их намного превышает размеры в других направлениях. Даже при небольшой концентрации раствора под влиянием межмолекулярных сил макрочастицы непрочно сцепляются и переплетаются друг с другом, образуя пространственную молекулярную сетку-каркас, препятствующую истечению раствора по капилляру. Это сильно увеличивает вязкость растворов ВМС.

Вязкость растворов ВМС зависит от:

1. Давления. Длинные макромолекулы ВМС располагаются поперек потока и оказывают большое сопротивление. При увеличении внешнего давления на жидкость макромолекулы ориентируются вдоль потока, т.е. сопротивление движения уменьшается и в результате вязкость раствора падает.

2. Концентрации. С увеличением концентрации вязкость растворов ВМС резко возрастает, так как усиливается межмолекулярное взаимодействие.

3. Времени. Со временем структурирование усиливается и вязкость возрастает.

4. Температуры. Для разветвленных макромолекул ВМС с увеличением температуры вязкость уменьшается. Линейные ВМС при повышении температуры сильно изгибаются и препятствуют ориентации макромолекулы в потоке и вязкость возрастает.

5. Механического воздействия. Встряхивание, механическое перемешивание разрушает трехмерную сетку-каркас, и вязкость возрастает.

6. Кислотности раствора (рН). рН раствора влияет на электрический заряд макромолекулы и, как следствие ее форму. В ИЭТ макромолекулы белка имеют форму глобулы и при этом структурирование минимальное и вязкость минимальная.

7. Добавления солей. Влияние ионы оказывают различное. Это связано с различной их способностью гидратироваться. Например, сульфат-ионы хорошо отнимают воду, при этом межмолекулярное взаимодействие усиливается, и вязкость возрастает.

Применительно к растворам высокомолекулярных соединений используют следующие величины: ηотн – относительную вязкость, представляющую собой

отношение вязкости раствора (η) к вязкости растворителя (ηо); ηуд – удельную вязкость ; ηпр – приведенную вязкость, равную отношению удельной

вязкости к концентрации С

Предел приведенной вязкости при концентрациях полимера, стремящихся к нулю,

называется характеристической вязкостью – . Характеристическая вязкость связана с молекулярной массой полимеров следующим образом:

Закон Пуазейля лежит в основе вискозиметрии – метода определения вязкости раствора. Этим методом определяется вязкость раствора по времени истечения объёма жидкости из трубки.

Вопросы для самоконтроля

1. Какие вещества относятся к высокомолекулярным? Классификация ВМС.

2. Сходство растворов ВМС с гидрофобными коллоидами.

3. Отличительные особенности ВМС (сравнить с коллоидами).

4. Набухание ВМС: стадии, факторы, скорость и степень набухания.

5. Электрические свойства растворов ВМС. Изоэлектрическая точка.

6. Диффузия и осмос в растворах ВМС. Осмотическое давление растворов ВМС.

7. Оптические свойства ВМС: светорассеяние и поглощение.

8. Аномальная вязкость растворов ВМС. Факторы, влияющие на вязкость растворов.

9. Три грамма желатина через 60 мин поглотили 8 г воды. Определите степень набухания

(Ответ: 267 %).

10. К какому электроду будет передвигаться частица белка при электрофорезе, если его ИЭТ = 4, а рН раствора равен 5? (Ответ: к аноду)

11. Рассчитайте молекулярную массу образца, если уравнение для раствора полистирола в толуоле имеет следующий вид: [η] = 0,105 = 1,7·10^-5·М^0,69 (Ответ: 312000).

Лекция 14

СТРУКТУРООБРАЗОВАНИЕ В КОЛЛОИДНЫХ РАСТВОРАХ.

ГЕЛИ И СТУДНИ

14.1. Процессы структурообразования в коллоидных системах

Дисперсные системы, стабилизированные в такой степени, что исключается возможность сцепления частиц дисперсной фазы при их сближении, можно рассматривать как системы лишенные структуры. К таким бесструктурным системам относятся, в частности, устойчивые гидрозоли, стабилизированные суспензии и др. Частицы стабилизированной суспензии, осевшие под действием силы тяжести, хотя и сближены, но не связаны какими-либо силами, поэтому такая система в присутствии жидкости является бесструктурной.

При понижен устойчивости системы сближающиеся частицы могут сцепляться между собой. Сцепление, происходящее в отдельных точках поверхности частиц, создает более или менее рыхлую структуру. Если взять две суспензии одинакового состава, причем одна из них стабилизирована, а в другой стабилизация отсутствует, то в стабилизированной суспензии объем осадка будет меньше, чем в нестабилизированной, так как частицы, не связанные друг с другом, укладываются более плотно. В нестабилизированной системе образовавшиеся между частицами связи препятствуют более плотной упаковке даже при наличии промежутков в тех местах, где частицы не имеют непосредственного контакта.

14.2. Гели и студни. Определение. Классификация

Студни или гели – это дисперсные системы, где дисперсная фаза состоит из коллоидных частиц или макромолекул ВМС, соединенных в виде пространственной сетки, ячейки которой заполнены дисперсионной средой.

Гели широко распространены в природе: каучук, желатин, целлулоид, столярный клей, текстильное волокно, биологические ткани (стекловидное тело глаза, мышечные ткани, коллаген, хрящи, клеточные оболочки, оболочка эритроцитов, протоплазма), продукты питания (тесто, хлеб, мармелад, различные желе, карамель), минералы (опал, агат).

Студни классифицируются:

1) В зависимости от природы дисперсионной среды на:

· Гидрогели (вода) · Алкогели (спирты) · Бензогели (бензол)

2) В зависимости от количества дисперсионной среды:

· Малое содержание дисперсионной среды (сухие студни или ксерогели: крахмал, сухой желатин, столярный клей; сложные ксерогели (мука, печенье, сухари)

· Большое содержание дисперсионной среды, т.е. сухого остатка (дисперсной фазы) ~1-2 % и менее (лиогели: кисель, мясной студень, простокваша, растворы мыла и моющих средств)

3) Отдельная группа гелей – коагели:

· Студенистые осадки, которые образуются при коагуляции лиофобных золей

Fe(OH)3, H2SiO3 и др.

· Хлопьевидные осадки ВМС, полученные при высаливании белков, нуклеиновых кислот, полисахаридов.

Коагели неоднородны, частицы разного размера, содержат небольшое количество дисперсионной среды.

4) В зависимости от природы веществ, образующих гель, прочности связей:

· Хрупкие или неэластичные гели. Получают из нерганических соединений и построены из жестких частиц (например, студни Fe2O3, SnO2, TiO2, H2SiO3)

· Эластичные гели (или студни). Образуются из органических веществ – гибких макромолекул ВМС.

5) По происхождению:

· Естественные гели (студни желатина, природного агар-агара, биологических тканей)

· Искусственные гели (синтетические каучуки, нитроцеллюлоза и др.).

14.3. Строение гелей и студней

А) Хрупкие гели образуются из неорганических веществ. Жесткие частицы дисперсной фазы образуют мелкопористую структуру из множества узких жестких капилляров, диаметр которых 20-40 Å. Смачивающие гель жидкости заполняют капилляры, при этом увеличения объема геля не происходит, поэтому эти гели называются еще ненабухающими.

Б) Эластичные гели получают из органических веществ – макромолекул ВМС. Имеют структуру трехмерной сетки или каркаса с крупными ячейками, заполненными дисперсионной средой. Благодаря гибкости макромолекул ВМС эластичный каркас легко и обратимо меняет свою форму под действием внешней силы и восстанавливают ее. Эластичные гели ограниченно набухают в родственных по химическому составу жидкостях, при этом сильно изменяется объем геля.

14.4. Методы получения гелей

1) Физические методы. В основе лежит создание условий, чтобы из дисперсной фазы и дисперсионной среды образовался гель:

· Изменение температуры · Изменение рН · Подбор растворителя

2) Химические методы

· Основаны на реакции полимеризации или поликонденсации, двойного обмена

· Часто студни образуются в результате ферментативных и бактериостатических процессов (например, получение кефира, простокваши, створаживание молока и др.)

Физические и химические методы делятся на 2 основные группы:

1. желатинирование (гелеобразование)

2. ограниченное набухание ВМС

Желатинирование – это процесс превращения легкоподвижного золя или вязкотекучего раствора ВМС в твердообразный нетекучий гель или студень.

Процесс желатинирования можно представить следующим образом: вначале мицеллы золя или макромолекулы раствора ВМС находятся в броуновском движении. При определенных условиях движение замедляется, вязкость растворов увеличивается, мицеллы или макромолекулы сталкиваются друг с другом и соединяются с помощью

сил Ван-дер-Ваальса или химических связей, образуется пространственная сетка (каркас), которая пронизывает весь объем дисперсной системы. В ячейках содержится дисперсионная среда.

Процесс гелеобразования зависит от факторов:

1. Форма и размер мицеллы золя или макромолекулы ВМС. Необходимым условием гелеобразования является ассиметричная форма мицеллы или макромолекулы. Чем выше ассиметрия частиц, тем быстрее и при более низких концентрациях дисперсной фазы образуется гель. Лучше, когда частица имеет удлиненную форму. Если форма частицы призма, то концентрации раствора должна быть больше. Еще большей концентрации должен быть раствор, если частицы в форме шара, куба.

2. Концентрация раствора. Чем больше концентрация раствора, тем быстрее образуется гель.

3. Температура. С ростом температуры гелеобразование замедляется. При увеличении температуры интенсивность броуновского движения коллоидных частиц или макромолекул ВМС возрастает. Следовательно, связь между молекулами ослабевает, прочность каркаса уменьшается, и гель переходит в золь. При повышении температуры увеличивается и минимальная концентрация дисперсной фазы, при которой наступает застудневание.

4. Прибавление электролита. При добавлении электролитов одни ионы ускоряют процесс застудневания, другие замедляют или вовсе устраняют его. Главным образом, влияют анионы. Улучшают процесс застудневания ионы, обладающие высокой гидратирующейся способностью. Например, ионы SO4^2- энергично дегидратируют молекулы ВМС, что благоприятствует их взаимодействию и образованию студней.

5. Влияние времени. Застудневание, даже при низкой температуре, требует продолжительного времени (от минут до недели) для образования ячеистой структуры.

6. Влияние рН. Скорость желатинирования белков выше при рН = ИЭТ, т.е. когда отсутствует электрический заряд и макромолекула менее гидратирована.

Ограниченное набухание - это самопроизвольный процесс. При набухании имеет место одностороннее проникание низкомолекулярного растворителя между макромолекулами полимера. Набухший полимер – термодинамически устойчивый раствор низкомолекулярного растворителя в полимере. Набухший полимер увеличивается и в объеме, и в массе. Наличие внешнего давления способствует проникновению растворителя в каркас геля, т.е. способствует набуханию.

14.5. Свойства студней

Гели и студни имеют ряд общих свойств с твердыми телами. Это наличие собственной формы, механических свойств (упругости, эластичности).

К специфическим свойствам студней относятся тиксотропия и синерезис (или старение):

· Тиксотропия – обратимое превращение нетекучего геля в раствор в результате механического воздействия. При встряхивании или перемешивании разрушаются слабые Ван-дер-Ваальсовые межмолекулярные связи, т.е. разрушается трехмерная структура геля и образуется текучий раствор. Но через некоторое время структура самопроизвольно восстанавливается и снова образуется гель. В некоторых случаях хрупкие гели (например, гель кремневой кислоты) в результате механического воздействия необратимо разрушаются.

· Со временем гели стареют, на их поверхности появляются капельки жидкости разбавленной дисперсионной среды (разбавленный коллоидный раствор или раствор ВМС). Затем капельки сливаются и образуют жидкую фазу. Происходит разделение студня на 2 фазы. Механизм синерезиса: под действием внешних факторов частицы дисперсной фазы геля сближаются, структурная сетка уплотняется, дисперсионная среда, заключенная в ячейках каркаса, выдавливается на поверхность геля. После синерезиса гель уплотняется, уменьшается в объеме, но сохраняет прежнюю форму.

Вопросы для самоконтроля

1. Процесс структурообразования в коллоидных растворах.

2. Гели и студни. Классификация и строение.

3. Способы получения гелей и студней.

4. Желатинирование растворов ВМС. Механизм, примеры. Факторы, влияющие на скорость желатинирования.

5. Свойства студней: тиксотропия, синерезис.

DG_x_. _p_.

Þ K_P = e^-

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

25.10.2024