Тема урока: «Решение показательных уравнений и неравенств»

 

Тема учебного раздела: Показательная функция

Место урока в теме: заключительный (обобщающий) урок в данном разделе.

Продолжительность: 40 минут.

Предмет, класс, в котором используется продукт: алгебра, 10  класс.

Авторы учебника, учебно-методического комплекта: Алгебра и начала математического анализа. 10-11 классы: учеб. для общеобразоват. учреждений: базовый уровень/ Ш.А.Алимов, Ю.М.Колягин, М.В. Ткачёва и др./ .

Тип урока: урок обобщения и систематизации знаний и способов действий в сочетании с их комплексным применением.

Оборудование: персональный компьютер (ПК) учителя, мультимедийный проектор, презентация к уроку, дидактические материалы (цветные карточки с заданиями, сигнальные карточки, карточки для самостоятельной работы, для домашнего задания), оценочные листы, карта «Рефлексия».

Формы организации труда: блиц-опрос, индивидуальная, работа в паре, рефлексия.

Форма проведения: урок-практикум.

Методы обучения: словесный, наглядный, практический.

Пояснительная записка: при  подготовке урока в 10 классе  я руководство-валась возрастными особенностями учащихся и государственным стандартом по математике (алгебра).

Основные понятия урока: Показательная функция, график показательной функции, показательное уравнение, показательное неравенство, способы решения показательных уравнений и неравенств.

 

Цели урока:

обучающие:

- создать условия для повторения свойств показательной  функции; способы решения  показательных уравнений и неравенств;

    - систематизировать знания учащихся по теме, закрепить умение применять их, выявить  «скрытые» проблемы и затруднения, определить степень усвоения материала;

-         формирование заинтересованности учащихся в решении показательных уравнений и неравенств при подготовке к ЕГЭ;

-         подготовиться к контрольной работе.

 

развивающие:

-         развивать у учащихся умения анализа условия задачи перед выбором способа её решения;

-         способствовать развитию познавательного интереса, навыков самоконтроля и самооценки;

-         развивать умение обобщать, абстрагировать и конкретизировать знания по изученной теме;

воспитательные:

-         способствовать активности, организованности, умению общаться.

 

План урока.

1.      Организационный момент  (1 мин).

2.      Постановка целей и задач  (2 мин).

3.      Актуализация опорных знаний. Блиц-опрос (5 мин).

4.      Математический диктант (6 мин).

5.      Диагностика уровня формирования практических навыков.(3 мин)

6.      Решение показательных уравнений и неравенств (15 мин)

7.      Пауза (1 мин)

8.      Диагностика уровня освоения учащимся знания (5 мин)

а) Найдите ошибку.

б) Верно ли что?(если успеем)

9.      Домашнее задание.(1 мин)

10.  Рефлексия. Итоги урока. Оценки. (1 мин)

 

Ход урока.

1.   Организационный момент. Приветствует учащихся, определяет отсутствующих. Проверяет готовность к уроку.

2.  Постановка целей и задач.

Через 1,5 года вы подойдёте к важной черте вашей жизни к итоговой аттестации. С какими заданиями вы уже можете справиться? Что вы изучали на последних уроках?

Сегодня  у нас урок обобщения по теме «Решение показательных уравнений и неравенств»  Откройте тетради и запишите число и тему урока. (слайд 2)

- Как вы считаете, что мы должны повторить на уроке?

-Давайте вместе сформулируем цели сегодняшнего урока.

(слайд 3)

( формулируют цели : повторить всё, что знаем о показательной функции, обобщить, закрепить и систематизировать знания методов решения показательных уравнений и неравенств)

- Все виды работ  на уроке будут оценены и занесены в рабочие листы учёта знаний, которые есть у каждого из вас. В эти листы вы будете вносить, свои полученные  баллы за каждый этап урока. Часть баллов поставит вам сосед по парте, а часть я - если сочту необходимым. Затем по общему количеству набранных баллов вы получите оценку за урок.

 

3.     Актуализация опорных знаний. Блиц-опрос.

( в рабочем листе, ставите себе «плюс» за каждый верный ответ)

Вопросы к классу: В основе решения показательных  уравнений и неравенств лежит знание свойств степени и свойств показательной функции, вспомним их.

(один человек  работает у доски. Задание «Найти пару».  Восстановите формулы, выражающие свойства степеней с рациональным показателем)

(слайд 4)

1. Какая функция называется показательной?

    (функция вида у=а^х, где а и а 1)

2. Какова область определения показательной функции у = 4^х?

(множество R всех действительных чисел)

3. Какова область значения показательной функции у= 4^х?

   (множество всех положительных чисел)

4. При каком условии показательная функция является возрастающей?

                                    (а

5. При каком условии  функция является убывающей?  (0

(слайд 5)

    6. Что общего у графиков этих двух функций?

(слайд 6)

7. Возрастает или убывает показательная функция:

    а) у =                б) у = 7^х                 в) у= 0,8^х  

8. Для чего необходимо знать свойства возрастающей и убывающей функции?  (для решения показательных неравенств)

9. Зная свойства возрастающей и убывающей  показательной функции, решите неравенства:  2³  2^х                  3^х  81

 

(слайд 7)

10. Какое уравнение называется показательным? (уравнение, в котором неизвестное содержится в показателе степени)

(уравнения вида , где а – положительное число, и отлично от 0, и уравнения, сводящиеся к этому виду)

11. Назовите методы решения показательных уравнений и неравенств:

        а) метод уравнивания оснований

        б) метод вынесения общего множителя за скобки

        в) метод введения вспомогательной переменной

        г) графический метод.

- Оцените свою работу, как поработали устно

(за каждый верный ответ 1 балл)

Хорошо, вспомнив основные теоретические вопросы,  переходим к следующей работе.

 

4.     Математический диктант (по вариантам) 6 мин.

У каждого ученика на парте приготовлен бланк для выполнения математического диктанта.  В этих бланках ученик либо сразу записывает ответ, либо выполняет решение, если это требуется. Перед проведением математического диктанта можно повторить правила его проведения.

(слайд 8)

Задания диктанта:

 1. Какие из указанных функций являются:

    а) возрастающими; б) убывающими

ВАРИАНТ 1                                                              ВАРИАНТ 2

а)    у = 5^х       б) у =                                  а) у =            б)    у= 8^х       

 

в) у = 49^-х       г) у=1,4^х                                                         в) у = 4,9 ^х             г) у=4^-х

 

(слайд 9)

2. Решите уравнение:    а) 2^х =32                              а) 5^х = 625

                                       б) 5^х-2 =25                          б ) 3^х-8 =27

                                       в) 3^х-1 =                              в) 6^х+12 =

 

(слайд 10)

 

3. Решите неравенство:

                                    а)  2^х  4                                            а)  5^х  125

                                    б)  2^х  -2                                           б)  5^х  -5

                                  в)   0,2^х0,2⁷                                                         в)  0,4^х0,4³

Проверка выполнения математического диктанта осуществляется учениками. (взаимопроверка). Учитель с помощью проектора выводит правильные ответы к заданиям математического диктанта на экран. Также на доске записаны критерии выставления оценки. После как ученики выставили оценки они сдают работу учителю.

Ответы к математическому диктанту: (слайд 11)

Критерии проверки:  10 баллов (максимум)

За каждый правильный ответ выставляется 1 балл.

     

       Диагностика уровня формирования практических навыков.

Продолжаем. (слайд 12)

Михаил Васильевич Ломоносов говорил: «Теория без практики мертва и бесплодна. Практика без теории невозможна и пагубна. Для теории нужны знания, для практики сверх того и умения». И вот теперь вы должны проявить свои умения при решении различных показательных уравнений и неравенств.

   (слайд 13)

Задание: (в паре)  Разбить уравнения и неравенства на группы по методу их решения и записать соответствующие номера в таблицу.

1)  2^2х-4  4                                   5)  = 3-х

2)                    6) 9  81^1-2х = 27^2-х

3)   27 ^{1-х =}                                    7) 5^х+1 + 5^х + 5^х-1 = 31

4)  3^х+2  -5 3^х = 36                        8) 2^х   3-х

     9)             10) 2^2х-1 +2^2х-2 +2^2х-3  448

Результаты занесите в таблицу:

Приведение к одному основанию	Вынесение общего множителя за скобки	Замена переменного (приведение к квадратному)
1, 3, 6	4, 7, 10	2,9

Давайте проверим,  что у вас получилось.  (слайд 14)

 

 Оцените свою работу.  Укажите количество верно определённых способов.

 

 

5.     Решение уравнений и неравенств по каждому способу у доски.

За каждое верно выполненное уравнение и неравенство получают по 2 балла.

(слайд 15)

                                                                                     

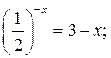
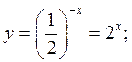
х	-1	-2	0	1	2	х 0 3 у 3 0     3
у			1	2	4	8

у

Х

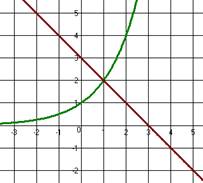
Ответ:

 

 

6.     Пауза

 

 

 

 

 

 

 

 

 

 

 

 

 

 

8.     Диагностика уровня освоения учащимся знания

  После решения уравнений и неравенств рассматривается задание

 « Найди ошибку в решении» . Для выполнения этого задания учащиеся пользуются бланком, который раздаёт учитель. Свои ответы можно сверить с правильными ответами на доске.

Решите уравнение: Решение:          х - 6 =  - 4          х=2

Решите неравенство:    Решение:          1-х х

 

 

 

 

 

 

Оцените свою работу.

Все ошибки найдены и исправлены- 6 баллов;

исправлены в 1 задании – 4 балла; другие варианты -1 балл.

 

Приём «Верные и неверные утверждения»

Верно ли утверждение, что…. (каждый раз называю это словосочетание)

Обоснуйте свой ответ.

1. Уравнение вида называется показательным.  (+)

2.  - это показательное уравнение   (-)

3. 4 является корнем уравнения      (+)

4. Корень уравнения  меньше корня уравнения (+)

5. - это показательное неравенство (+)

6. Корень уравнения  принадлежит промежутку    (-)

7. Корень уравнения  является  (+)

8. Показательное неравенство  равносильно неравенству , если а>1

    Оценка: за каждое верное обоснование по 1 баллу.

Выставляем оценку за последнее задание и выводим общую за урок.

 ****Применение показательной функции в природе и технике Показательные уравнения необходимы в биологии, в медицине, при исследовании морей и океанов. Находит важнейшее применении при изучении природных явлений, при описании размножения живых организмов, в технике и во многих других областях.

 

9.     Итог урока.  Домашнее задание. Рефлексия.

 

      Сегодня мы повторили свойства показательной функции, способы решения показательных уравнений и неравенств.  На дом вы получаете задание двух уровней из банка заданий ЕГЭ, выполните те, которые сможете, подготовьтесь к контрольной работе.

    В ходе  нашего урока в ваших рабочих листах появились баллы за работу на уроке. Посчитайте свой суммарный балл и согласно критериям, приведённым на доске поставьте себе оценку за усвоение темы «Показательная функция»

Критерии:   выше 25 баллов- оценка «5»

                     от 19 до 25 баллов –оценка «4»

                     от 13  до 19 баллов –оценка «3»

                     ниже 13 –оценка «2»

 

Рефлексия. Отметьте точкой на графике функции уровень своих полученных знаний сегодня на уроке:

- на графике возрастающей функции, если на уроке у меня не было проблем, я доволен своей работой;

- на прямой параллельной оси ОХ, если всё шло ровно, гладко, я работал неплохо;

-на графике убывающей функции, если встретились затруднения, мне было трудно на уроке.

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru