Конспект урока на тему: "Параллелепипед, куб. Площадь поверхности, объем параллелепипеда, куба."
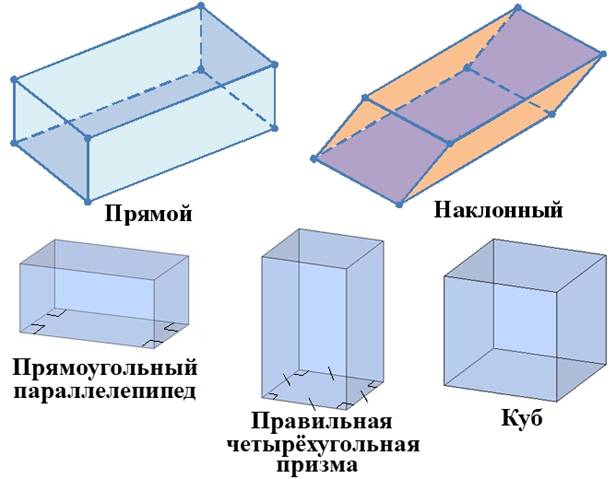
Тема: Параллелепипед, куб. Теорема Эйлера. Площадь поверхности, объем параллелепипеда, куба.
Параллелепипед — это четырёхугольная призма, все грани которой являются параллелограммами.
Прямоугольный параллелепипед, основание — прямоугольник.
Правильная четырёхугольная призма, основание — квадрат, высота призмы не обязательно равна стороне основания.
Куб, все рёбра куба равны, все грани — квадраты.
Длины не параллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями). У прямоугольного параллелепипеда три линейных размера.
Свойства параллелепипеда:
- Противоположные грани параллелепипеда равны и параллельны.
· Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
- Боковые грани прямого параллелепипеда — прямоугольники.
- Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. d 2 = a 2 + b 2 + c 2.
Площадь поверхности и объём параллелепипеда, куба.
|
Призма |
Рисунок |
Формулы для объема, площади боковой и полной поверхности |
|
Куб |
|
V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. |
|
Прямоугольный параллелепипед |
|
V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc+2ab, где |
|
Прямой
параллелепипед, параллелограмм со сторонами a, b и углом φ |
|
Sосн = ab sin φ, V = Sосн h = abh sin φ, Sбок = 2ah + 2bh, Sполн = 2ab sin φ + 2ah +2bh, где |
|
Произвольный параллелепипед |
|
Sосн = ab sin φ, V = Sосн h = abh sin φ, V = Sперп с, Sбок = Pперп с, Sполн = 2ab sin φ + Pперп с, где |
Алгоритм решения задач (устно):
1. Чертим прямоугольный параллелепипед.
2. Подписываем вершины. Отмечаем на
чертеже упомянутые в условии точки. Соединяем линиями, где это
необходимо.
3. Ставим известные (заданные) значения прямо на чертеже.
4. Если получился треугольник внутри тела, то выясняем есть ли в нем прямой
угол и какой именно. Для этого пользуемся теоремами о перпендикуляре к
плоскости или о трех перпендикулярах.
5. Чертим этот треугольник на плоскости. На нем также отмечаем заданные и
искомые величины, если нужно, перенося числа с параллельных ребер.
6. Проводим необходимые вычисления по известным формулам. Как правило, это
будут теорема Пифагора и определения синуса и косинуса острых углов
прямоугольного треугольника.
Решение задач.
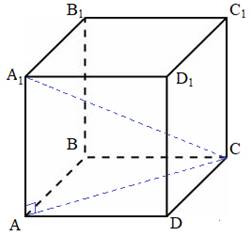Задача № 1. Найдите квадрат
расстояния между вершинами C и A1 прямоугольного
параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
Решение:
Рассмотрим прямоугольный треугольник AA1С в котором A1С является
гипотенузой. По теореме Пифагора
A1С2 = АA12 + AС2
В прямоугольнике ABCD: AC – диагональ, AB = CD. Значит,
AС2 = AD2 + СD2 = 16+25 = 41,
A1С2 = 9+41 = 50
Ответ: 50.
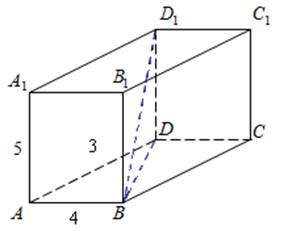Задача № 2. Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Дайте ответ в градусах.
Решение.
В прямоугольнике AA1D1D отрезок AD1 является диагональю, A1D1=AD. По теореме Пифагора
= 5.
Прямоугольный треугольник ABD1 равнобедренный: AB = AD1 = 5 значит, его острые углы равны 45º
Ответ: 45º.
Самостоятельное решение задач:
Задача №1. Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB= 4, AD = 3, AA1 = 5. Дайте ответ в градусах.
Задача №2. Найдите квадрат расстояния между вершинами B и D1 прямоугольного параллелепипеда, для которого AB = 5, AD = 5, AA1 = 3.
Задача №3. Найдите угол ACA1 прямоугольного параллелепипеда, для которого AB = 12, AD = 9, AA1 = 15. Ответ дайте в градусах.
Скачано с www.znanio.ru
Тема: Параллелепипед, куб. Теорема
Площадь поверхности и объём параллелепипеда, куба
Алгоритм решения задач (устно): 1
Самостоятельное решение задач:
© ООО «Знанио»
С вами с 2009 года.
