
Предмет: Алгебра и начала математического анализа.
Программа: Составитель Т.А. Бурмистрова. Алгебра и начала математического анализа.// Программы общеобразовательных учреждений. Издательство: Москва: Просвещение; 2009 г.
Учебник: Колягин Ю.М. и другие. Алгебра, 10 класс. – М.: Просвещение, 2009 г.
ТЕМА: Решение тригонометрических уравнений
МЕСТО УРОКА В ТЕМЕ.
Данный урок
– первый из трёх в теме «Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения».
− девятый по теме «Тригонометрические уравнения» и изучается сразу же после решения простейших тригонометрических уравнений
Тип урока.
- урок усвоения нового материала
Форма проведения:
Урок - лекция
ЦЕЛИ:
1. Обучающая:
Научить решать некоторые виды тригонометрических уравнений (квадратные) относительно одной из тригонометрических функций, однородные уравнения первой и второй степени относительно sinx и cosx
2.Развивающая:
Продолжить работу над умением самостоятельно делать выводы в результате анализа и синтеза изучаемого материала.
Работать над грамотной речью, над формированием познавательной мотивации, словесно-логического мышления, развивать культуру мысли.
3. Воспитательная:
Воспитывать трудолюбие, самостоятельность и умение преодолевать трудности, продолжить работу над правильной самооценкой.
4. Диагностическая:
В результате ученик осознаёт необходимость новых знаний по теме «Тригонометрические уравнения»;
знает о существовании нескольких способов решения тригонометрических уравнений;
выделяет теоретические положения, определяющие каждый из указанных выше способов;
выделяет действия, составляющие решение тригонометрического уравнения;
обосновывает ход рассуждений в процессе совместного с учителем решения тригонометрического уравнения
Оборудование:
классная доска, компьютер, мультимедийный проектор, экран, слайды.
У детей: учебник, тетрадь, ручка, простой карандаш, памятка с формулами для решений простейших тригонометрических уравнений.
Методы работы:
· Репродуктивный
· Частично- поисковый
ИСХОДНЫЙ УРОВЕНЬ состояния знаний, умений и навыков к данному уроку.
· Дети знают определение sinx, cosх, tgх, ctgх.
· Дети знают основное тригонометрическое тождество.
· Дети знают тригонометрические формулы: сложения, двойного угла, половинного угла, суммы и разности,
произведения, приведения, зависимости между синусом, косинусом и тангенсом одного и того же угла.
· Дети знают понятие поворота точки вокруг начала координат.
· Дети знают, как радианную меру перевести градусную и наоборот.
· Дети знают формулы для решения простейших тригонометрических функций.
· Дети умеют пользоваться тригонометром.
· Дети умеют решать простейшие тригонометрические уравнения sinx=а, cosх=а, tgх=а, ctgх=а.
Оформление:
Эпиграф:
Математика есть такая наука, которая показывает, как из знаемых количеств находить другие, нам ещё неизвестные.
Д.С.Аничков
Методические комментарий.
Учащиеся изучают три вида тригонометрических уравнений.
1) Уравнения, представляющие собой квадратные уравнения относительно какой-либо тригонометрической функции, либо сводимые к нему. Если в уравнение входят разные тригонометрические функции, то их, если возможно, надо выразить через одну. При этом следует выбирать эту функцию так, чтобы получилось квадратное относительно нее уравнение. Введя вспомогательную переменную и решив квадратное уравнение, переходим к решению одного из простейших тригонометрических уравнений.
2)Решение уравнений, левая часть которых разлагается на множители, а правая равна нулю, если хотя бы один из множителей равен нулю, а остальные (при этом значении переменной) имеют смысл, также сводится к решению простейших тригонометрических уравнений и к проверке того, не теряют ли смысл остальные множители при этом значении переменной.
3)Однородные уравнения первой и второй степени относительно синуса и косинуса или сводимые к ним, решаются особым способом, рассмотренном в учебном пособии. Часто однородные уравнения в начальном виде не очевидны, но могут быть преобразованы в явно однородные.
|
1. 2. 3.
4.
5.
6. 7.
|
ПЛАН УРОКА Организационный момент. Объявление темы и цели урока. Актуализация знаний в форме самостоятельной работы на решение простейших тригонометрических уравнений; Объяснение нового материала; 1) обобщение, выводы; 2) изучение теории по учебнику. Закрепление нового материала. 1) обучающая самостоятельная работа в тетрадях, упражнения на слайдах Подведение итогов. Домашнее задание. |
1 мин 2 мин 7 мин
20мин
12 мин
2 мин 1 мин |
|
Этапы урока |
Содержание урока |
Психолого-педагогическое обоснование |
|||||||||||||||||||||||||||
|
Учитель |
Ученик |
||||||||||||||||||||||||||||
|
1. Оргмомент. |
Здравствуйте, дети! Садитесь. Начинаем урок алгебры. Прочтите эпиграф к сегодняшнему уроку. Как вы его понимаете? |
Дети читают. - Узнаем что-то новое, нам ещё неизвестное. - С помощь изученного решим что-то другое и т.д. |
Эмоциональный настрой на урок. Вызываю мотивацию узнать новое. |
||||||||||||||||||||||||||
|
2. Тема и цели урока. |
Сегодня на уроке продолжим работу над изучением раздела «Тригонометрические уравнения», познакомимся с новыми видами тригонометрических уравнений, и выясним, по каким признакам их подразделяют. Тема для вас очень важная, как вы думаете, почему я так считаю? К концу урока вы должны решить самостоятельно три уравнения нового вида, и если понадобится моя помощь, то не стесняйтесь обращаться за ней. |
Возможные ответы: Такие уравнения придется решать на выпускном экзамене… Возможно пригодятся мне в техникуме или ВУЗе … |
Согласно психологопедагогической характеристике у большей части класса социальная мотивация, поэтому для многих главная учебная цель - успешно сдать выпускные экзамены. Мотивирую долговременное запоминание. Создаю условия для принятия цели. |
||||||||||||||||||||||||||
|
3. Актуализация знаний |
Любой день надо начинать с зарядки, а урок с разминки. Повторим пройденный материал. Установите соответствие между уравнениями и ответами: УРАВНЕНИЯ: 1. 2 sinx=1 2. 3. -2 cosx=1 4. -2 sinx=1 5. -2cosx= 6. sin(2 7. соs(2 8. tg(4 9. cos2x= 10. sin3x= 11. cos3x=
12. sin2x= ОТВЕТЫ: 1. 2. (-1)n 3. 4. (-1)n 5. (-1)n 6. (-1)n 7. 8. (-1)n+1 9. 10. 11. 12.
|
Дети расставляют цифры в заранее приготовленные бланки, после меняются бланками и по слайду проводят взаимное оценивание: 12заданий – оценка 5 9-11 заданий – оценка 4 6-8 заданий – оценка 3 менее 6 заданий – оценка 2
Ученики выполняют упр. самостоятельно. Проверка – взаимопроверка.
|
Формирую умение общаться друг с другом, посредством включения в групповую работу с распределением обязанностей, рецензирования ответов, организация взаимоконтроля и взаимопроверки.
|
||||||||||||||||||||||||||
|
4. Работа по теме урока. Объяснение нового материала
чтение выводов по учебнику
обобщение, выводы
|
Рассмотрим основные виды тригонометрических уравнений и способы их решений. Для большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений, после чего они сводятся к решению простейших уравнений вида sinx=а, cosх=а, tgх=а, ctgх=а. Во время объяснения вы слушаете, а записи в тетради делайте после обсуждения pешения упражнения на доске. Каждый ученик должен воспроизвести это решение в тетради по памяти. Учитель, проходя по классу, контролирует процесс воспроизведения по памяти записей в тетради и оказывает помощь детям с низким уровнем развития слуховой и визуальной памяти. Уравнения, сводящиеся к алгебраическим: 1)аsin2 х + bsinх + с =0, а≠0
решаются заменой. Пусть t = sin
х,
Тогда уравнение примет вид at2+bt+c=0 2) а cos2x + bsinх + с =0, а≠0 можно свести к квадратному относительно sinх, если заменить cos2x на 1 - sin2 х
Аналогично поступают с уравнениями: 1)а cos2x + bcosx + с =0, а≠0 2) а sin2х + bcosx + с =0, а≠0 Откройте учебники на 323-324 и найдите основные принципы решения уравнений, сводящихся к алгебраическим.
Далее на доске разбираются два примера. а)8 cos2x +6sinx-3=0 Как это уравнение преобразовать к записи с использованием одной тригонометрической функции?
б)При каких значениях х принимают равные значения функции у=1+ cosх; у= - cos2х
Уравнения вида asin х + Ьсоs х = 0, asin2 х + b sin х cos х + ccos2 х = 0 В каждом слагаемом левых частей этих уравнений сумма степеней синуса и косинуса одна и та же. В первом уравнении она равна1. Такие уравнения называют однородными. Уравнение asin х + Ьсоs х = 0, называется однородным уравнением первой степени относительно sin х и cos х. При а≠0 равносильно atg х + b = 0. Уравнение asin2 х + b sin х cos х + ccos2 х = 0 называется однородным уравнением второй степени относительно sin х и cos х. Если а≠0, то разделим обе части уравнения на cos2х≠0. Получаем уравнение atg2 х + btg х + с = 0. Если a= 0, то уравнение принимает вид b sin х cos х + c cos2 х = 0 и решается разложением на множители левой части: cos х (bsin х + ccos х) = 0. Уравнение вида asin х + Ьсоs х = с, где
а
и
b не равны
нулю одновременно, может быть сведено к однородному, если sin
х
и
cos х заменить
по формуле двойного аргумента, а правую часть умножить на sin2 Получаем: 2аsin
(b +
с)
sin2 Далее уравнение решается как обычное однородное уравнение второй степени.
Решите уравнение 1)3sin2 х + sin х cos х =2cos2 х.
Прежде, чем дети поделят равенство на cos2 х, учитель обосновывает то, что cos х≠ 0.
Докажем методом от противного, что cos х≠ 0. Предположим, что cos х =0, тогда из уравнения видно, что и sin х = 0, что невозможно, так как не выполняется тождество sin2 х + cos2 х = 1.
2)Уравнение такого вида sin 2х + sin2 х =0 является однородным, если sin2х заменить по формуле двойного аргумента, то есть привести уравнение к виду 2sin х cos х + sin2 х = 0. Здесь отсутствует член, содержащий cos2х. Поэтому, чтобы степень уравнения не понизилась, делим все на cos2х≠0; уравнение tg2х + 2tgх = 0 - это неполное квадратное уравнение относительно tgх. Решаем его, разложив левую часть на множители: tg х (tg х + 2) = 0. Отсюда tg х = 0 или tg х = - 2, то
есть х=
или х
= - arctg 2 + Можно данное уравнение решать не переходя к тангенсу, а сразу разложить на множители. 3)Уравнение 3sin2 х - 4sin х cos х + 5cos2 х = 2 тоже приводится к однородному, если правую часть умножить на выражение sin2 х + cos2 х, равное 1, Это уравнение в результате приводится к виду sin2 х - 4sin х cos х + 3cos2 х = 0. 4)Решите уравнение 1 + cos х + cos 2х = 0. Решение. Выражение 1 + cos2х заменим выражением 2cos2 х. Тогда уравнение принимает вид 2cos2 х + cos х =0. Разложим левую часть этого уравнения на множители: cos х (2cos х + 1)=0. Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом не теряет смысла, то есть cos
х
= 0, х
= 2cos х + 1 = 0, 2cos х = - 1, cos х = - x = Ответ: x = НА ЗАМЕТКУ: 1. При решении однородных уравнений обязательно нужно обосновывать, что cos х≠ 0. В этом примере дан один из способов обоснования, в других примерах это делается другим способом. 2.При решении уравнения можно не вводить новую переменную, а решать квадратное уравнение относительно tg х. 3.При решении тригонометрических уравнений, решаемых разложением на множители, нужно использовать все известные способы разложения на множители: вынесение общего множителя за скобки, группировка, применение формул сокращенного умножения и деления, искусственные приемы.
|
Во время объяснения у доски решения уравнений учащиеся ничего не записывают в тетрадях. Весь класс смотрит на доску и мысленно прорабатывает каждый этап решения. После объяснения учителя, один из учеников устно проговаривает последовательность решения. После чего решение с доски убирается, а учащиеся по памяти воспроизводят решения в тетради.
Дети работают с учебником, учатся находить и выделять главное.
Поиск нужного преобразования не займёт много времени у детей. Заменяя cos2х на 1- sin2х получаем 8(1- sin2х)+6 sinх-3=0 8 sin2х-6 sinх-5=0 Пусть sinх= t. Тогда 8t2 – 6t-5=0 t1 Уравнение sinх= sinх не может быть больше 1. sinх= х=(-1)n+1 Ответ: х=(-1)n+1
Для нахождения значений х решим тригонометрическое уравнение 1+ cosх = - cos2х Дети подбирают нужное преобразование cos2х=2 cos2х-1 и получают неполное квадратное уравнение относительно cosх, которое решается вынесением множителя за скобки. 2 cos2х+ cosх=0 Ответ:
В процессе лекции после решения каждого задания один ученик должен дать обобщение или сделать вывод. Другие ребята могут дополнять ответ.
Решение. 3sin2 х + sin х cos х - 2cos2 х = 0. (*) Имеем однородное тригонометрическое уравнение второй степени. Разделив почленно обе части уравнения на cos2 х, получим 3tg2 х + tg х - 2 = 0. Для решения уравнения обозначим tg х через т, имеем 3 т 2 +т-2=0 т1= -1; т2=2/3 tg х = - 1, х
= arctg (- 1) + х
= -
tg х=2/3 х
= arctg 2/3 + Ответ: х
= -
х
= arctg 2/3 +
Данное уравнение дети дорешивают самостоятельно по ранее проговоренному алгоритму. Ответ: х= х
= arctg 3 +
Дети должны узнать по-другому сформулированное задание, воспользоваться предложенной заменой, продолжить преобразования и назвать ответ. Задание конспектируют в тетрадь. Ответ:
|
Использую коллективный способ обучения старшеклассников - лекцию. Выбор репродуктивного метода работы как основного (повтори…, воспроизведи…) на уроке обусловлен психологопедагогической характеристикой класса. Репродуктивный метод должен сочетаться с другими методами. Для поиска решения задач использую частично-поисковый. При его использовании школьники привлекаются к созданию гипотезы, решению задач путем наблюдения...
Учащиеся повторяют, сделанные выводы и записывают их в тетрадь. Работа по развитию зрительно-слуховой памяти.
Форма работы с заданием, если возникли затруднения, – это система наводящих вопросов: Какие формулы зависимости между синусом и косинусом вы знаете? Какая нам подойдёт? И т.д.
Погружение в нестандартную ситуацию. 1. Применение частично-поискового метода. Частично-поисковый метод учения является сочетанием восприятия объяснений учителя учеником с его собственной поисковой деятельностью по выполнению работ требующих самостоятельного прохождения всех этапов познавательного процесса. 2. Развитие мышления на этапе применения знаний к решению математических и учебных задач. Большинство справится с поставленной задачей, пусть и не с самого начала. Возникнет ситуация успеха.
Развиваю устную и письменную математическую речь на этапе применения знаний: формулировка приёмов, используемых при решении; правильное оформление решений типовых задач по образцам, приведённым в учебнике или тетради.
|
||||||||||||||||||||||||||
|
5. Закрепление нового материала. Обучающая самостоятельная работа с опорой на конспект . |
Обучающая
самостоятельная работа с обязательной проверкой и объяснением (два ученика
выполняют работу на
а)2 sin2 х + sin х-1=0 б)3sin2 х-5 sin х-2=0 а)3sin2 х+ sinх cos х= 2cos2 х б)2cos2 х-3 sin х cos х +sin2 х=0
сos5х –cos3х=0 |
Дети выполняют задание с помощью конспекта лекции и опорных карточек с формулами.
Дети выполняют обучающую самостоятельную работу по вариантам: I под буквой а; II под буквой б. Третье задание для всех.
|
Обучаю работе по алгоритму, работе с конспектом. Обратная связь даёт возможность выяснить, как дети поняли новый материал. Если задание решено не правильно, прошу объяснить, как ребёнок размышлял, помогаю найти ошибку. Организую помощь в деятельности ученика, проявляю внимание к его деятельности. При такой форме работы у детей вырабатывается математическая зоркость, чувство взаимопомощи. Учу работать самостоятельно, пользуясь конспектом-подсказкой. Обращаю внимание на то, что домашнее упражнение выполняется аналогично. Индивидуальная работа с учащимися. |
||||||||||||||||||||||||||
|
6. Подведение итогов урока. |
Что нового узнали на уроке?
Почему необходимо хорошо и быстро научиться распознавать виды тригонометрических уравнений?
Как определить какие преобразования лучше выполнить?
Учитель хвалит и оценивает ребят, справившихся с заданием обучающей самостоятельной работы лучше всего, не забывая подбодрить остальных, ведь впереди ещё два урока на отработку умений и навыков. |
Ученики правильно делают выводы и обобщения, так как поняли новый материал. Уравнения, сводящиеся к алгебраическим: 1)аsin2 х + bsinх + с =0, а≠0 решаются заменой. 2) а cos2x + bsinх + с =0, а≠0 можно свести к квадратному относительно sinх, если заменить cos2x на 1 - sin2 х Уравнение asin х + b соs х = 0, называется однородным уравнением первой степени относительно sin х и cos х. При а≠0 равносильно atg х + b = 0. Уравнение asin2 х + b sin х cos х + ccos2 х = 0 называется однородным уравнением второй степени относительно sin х и cos х. Если а≠0, то разделим обе части уравнения на cos2х≠0. Получаем уравнение atg2 х + btg х + с = 0. Если a= 0, то уравнение принимает вид b sin х cos х + c cos2 х = 0 и решается разложением на множители левой части: cos х (bsin х + ccos х) = 0.
-Это экономит время. При решении однородных уравнений обязательно нужно обосновывать, что cos х≠ 0. При решении уравнения можно не вводить новую переменную, а решать квадратное уравнение относительно tg х. При решении тригонометрических уравнений, решаемых разложением на множители, нужно использовать все известные способы разложения на множители: вынесение общего множителя за скобки, группировка, применение формул сокращенного умножения и деления, искусственные приемы.
|
Организация самоанализа собственной деятельности учащихся.
Создание ситуации успеха и обстановки, вызывающей положительные эмоции
|
||||||||||||||||||||||||||
|
7. Домашнее задание.
|
Параграф 4(стр322-326) прочитать Стр327: № 50(4), 51(2;4),53(4). выполнять при помощи опорного конспекта сегодняшнего урока. |
Дети записывают домашнее задание в дневник. |
Рекомендации и советы на что обратить внимание, мною будут даны при контроле выполнения самостоятельной работы в классе. |
||||||||||||||||||||||||||


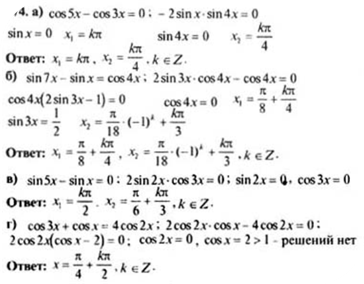
Самоанализ
урока алгебры и начала анализа в 10 классе.
Учитель: Соболева Анжела Юрьевна.
Тема: Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения.
Тип урока: Урок усвоения нового материала.
Данный урок является первым в теме «Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения». Учащиеся знают определение sinx, cosх, tgх, ctgх; основное тригонометрическое тождество; тригонометрические формулы; понятие поворота точки вокруг начала координат; как радианную меру перевести градусную и наоборот; формулы для решения простейших тригонометрических функций.
Учащиеся умеют пользоваться тригонометром и решать простейшие тригонометрические уравнения sinx=а, cosх=а, tgх=а, ctgх=а.
Научившись свободно распознавать виды тригонометрических уравнений дети научатся правильно их решать.
По результатам диагностики у 95% учащихся преобладают социальная и эмоциональная мотивация учебной деятельности. По уровню развития и обученности наибольшее количество детей относится к слабой группе (77%) и средней группе(23%). Для них характерны низкий уровень мышления, зрительная и слуховая память на среднем и низком уровне, внимание часто бывает неустойчивым. В связи с этим, для достижения цели урока, были подобраны упражнения с наглядной опорой, многократными повторениями, когда фронтальная работа сочеталась с самостоятельной работой.
Триединая дидактическая цель урока + диагностическая
1. Обучающая:
Научить решать некоторые виды тригонометрических уравнений (квадратные) относительно одной из тригонометрических функций, однородные уравнения первой и второй степени относительно sinx и cosx
2.Развивающая:
Продолжить работу над умением самостоятельно делать выводы в результате анализа и синтеза изучаемого материала.
Работать над грамотной речью, над формированием познавательной мотивации, словесно-логического мышления, развивать культуру мысли.
3. Воспитательная:
Воспитывать трудолюбие, самостоятельность и умение преодолевать трудности, продолжить работу над правильной самооценкой.
4. Диагностическая:
В результате ученик осознаёт необходимость новых знаний по теме «Тригонометрические уравнения»;
знает о существовании нескольких способов решения тригонометрических уравнений;
выделяет теоретические положения, определяющие каждый из указанных выше способов;
выделяет действия, составляющие решение тригонометрического уравнения;
обосновывает ход рассуждений в процесс совместного с учителем решения тригонометрического уравнения
Отбор и содержание материала сделаны в соответствии с программой, поставленными задачами и уровнем развития учащихся: фронтальная, индивидуальная, самостоятельная, практическая работа чередовались в ходе урока.
При объяснении нового материала были использованы методы - репродуктивный и частично-поисковый.
Считаю, что время на уроке было распределено рационально. Присутствует логика между этапами. Все этапы урока работают на главный. Этому способствует и отбор дидактического материала. Всё подчинено целям урока. На уроке присутствует контроль знаний в виде обратной связи: самостоятельной работы с элементами самопроверки и взаимопроверки, комментирования.
Считаю, что психологическая атмосфера на уроке нормальная. Стараюсь создать ситуацию успеха: похвала, неожиданная радость, эмоциональный настрой.
Считаю, что урок цели достиг. Все поставленные цели урока реализованы.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.