Конспект урока решение задач с помощью систем линейных уравнений, Макарычев

Урок в 7 классе

«Решение задач с помощью системы линейных уравнений с двумя переменными» (дистанционный)

Тип урока: урок изучения нового материала

Цели:

• закрепить знания и умения решения систем уравнений;
• научить детей решать задачи с помощью составления систем уравнений;
• использовать задачи из литературных произведений, развитие познавательного интереса при решении задач.

Планируемые результаты:

Научиться решать задачи с помощью составления систем линейных уравнений

Методы обучения:

• словесные (беседа, объяснение);
• наглядные (презентация к уроку);
• проблемные (организация поисковых действий нового способа решения задач и выработка его алгоритма);
• практические;

Наглядные пособия и оборудование: презентация, ПК, графический планшет, платформа ZOOM.

ХОД УРОКА

1. Подготовка к восприятию материала (проверка опорных знаний)(10 мин)

1. Учитель, восстанавливает изученную ранее тему. Детям задаются вопросы

·        Посмотрите на экран, какой математический объект вы видите? (Слайд 2)

·        Что является решением системы уравнений? (слайд 2)

·        Сколько решений может иметь система двух линейных уравнений с двумя переменными? Как это проверить? ( Слайд 3)

·        Какие способы решения систем уравнений вы знаете? (Слайд 4)

·        Давайте вспомним суть применения каждого способа на примере данной системы (слайд 5-7).

 2. Решить данную систему:

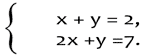
Графический метод (слайд 5)

Метод подстановки (слайд 6)

Метод сложения (слайд 7)

3. Составить математическую модель предложения (линейное уравнение с двумя переменными): (Слайд 8)

1. Мальчиков и девочек в классе 8 человек.

2. Учителей в классе на 3 человека меньше чем учеников.

3. Птиц на ветке (х) втрое больше чем под деревом(у).

4. В коробке лежат старинные трехрублевые и пятирублевые купюры, в сумме 50 рублей.

5. 60% одного числа равны 30 % другого.

6. За 1,5 часа по течению катер проплыл 60 км. (х-собственная скорость катера, у- скорость течения)

4. Система уравнений не только позволяет установить общие корни уравнений, содержащихся в ней, но и становится хорошим помощником при решении задач. В таких задачах неизвестных компонентов более одного и они связаны друг с другом условием. Сегодня мы рассмотрим задачи, в которых неизвестно два каких-либо элемента и будем учиться решать такие задачи с помощью составления системы уравнений. Тексты нескольких задач будем брать из литературных произведений.(Слайд 9)

 Вспомним отрывок из произведения А.П. Чехова «Репетитор» (слайд 10)

-Назовите героев рассказа?(купец Удодов, его сын Петя, семиклассник Зиберов Егор Александрович)

Кто читал произведение, тот помнит, что отец Удодов решил ее на счетах ("по-неученому"), т.е. арифметически, используя только действия с числами.

Сегодня решим эту задачу составляя систему уравнений.

Дети записывают в тетрадях число, тему урока 

2. Изучение новой темы.

А) Задача Зиберова:

Решаем на доске и в тетради (условие в виде таблицы)

Обозначим некоторые неизвестные буквами и, используя условие задачи, составим систему уравнений.

-Сколько неизвестных в задаче Зиберова?

-Введем буквенные обозначения.

-Какими условиями они связаны.

Пусть куплено х аршин черного сукна, у аршин - синего,

Составить систему уравнений по заданным условиям и решить, один ученик у доски, остальные учащиеся в тетради

3. Первичное закрепление изученного материала.

Рассмотрим для примера такую задачу.

№1.

Я знаю, что в классе 20 учеников. Среди них есть девочки и мальчики.? А еще я знаю, что девочек больше чем мальчиков на 4 человека. Сколько мальчиков и девочек в этом классе?

Обозначим x – количество девочек, а y - количество мальчиков

Т.к. мальчиков и девочек вместе - 20. Получим уравнение: х + у = 20

С другой стороны девочек больше чем мальчиков на 4

Значит можно получить следующее уравнение х - у = 4

Объединим оба эти уравнения в систему, т.к в каждом уравнении речь идет об одних и те же детях., получим:

Далее дети самостоятельно решают систему уравнений

Ответ: В классе 8 мальчиков и 12 девочек

№2.

В автопарке много машин. Среди них есть машины марок - "ауди" и "опель". Известно, что всего в автопарке -9 "ауди", а "опель" на 5 машин больше, чем "ауди". Сколько машин "ауди" и "опель" в автопарке ?

Решение:

Ответ: В автопарке 2 белых медведя и 7 бурых медведей.

4. Решение задач повышенного уровня сложности.

А) Задача из сказки "Тысяча и одна ночь".

Составьте систему к решению задачи из сказки №458 "Тысяча и одна ночь".

Мудрец задает юной деве задачу:

Стая голубей подлетела к высокому дереву. Часть голубей села на ветвях, а другие расположились под деревом. Сидевшие на ветвях голуби говорят расположившимся внизу: Если бы один из вас взлетел к нам, то вас стало бы втрое меньше, чем нас всех вместе, а если бы один из нас слетел к вам,то нас с вами стало бы поровну". Сколько голубей сидело на ветвях и сколько под деревом??

Вопросы:

-Сколько неизвестных? Обозначим их буквами.

- Сколько условий? Составим 2 таблицы.

-Какие величины? Заполняем таблицы

Решают эту систему ученики дома.

Ответ: 7 голубей на дереве, 5 под деревом.

5. Подведение итогов урока, выставление оценок.

- Итак, подведем итоги. Какая сегодня у нас была тема урока?

- Что нового вы узнали, чему научились?

- Остались ли у вас вопросы, на которые учитель должен будет ответить на следующем уроке?

6. Домашнее задание

1.     Составить и решить задачу, в которой вы можете узнать возраст своих родителей, с помощью системы уравнений.

2.     Творческое задание. Найдите задачи из произведений! Решите их. Проиллюстрируйте.