Конспект элективного курса по математике "Классическое определение вероятности"(7 класс)

Классическое определение вероятности. Благоприятствующие события. Вероятности событий. Противоположные события

Цель: изучение математического описания случайных событий

Задачи: - дать понятия: классическое определение вероятности, благоприятствующие события, вероятности событий, противоположные события;

              - учить решать задачи на классическое определение вероятности;

              - учить находить и различать благоприятствующие события, вероятности событий, противоположные события;

              - развивать логическое мышление, кругозор, математическую речь, интерес к математике.

Ход занятия

1. Классическое определение вероятности

Очень часто в рассматриваемых явлениях действительности имеется некоторая симметрия, позволяющая говорить о равновозможности событий. Равновозможными называются элементарные события, шансы которых одинаковы. Так, при бросании игральной кости, на верхней грани может появиться любая цифра: 1, 2, 3, 4, 5 или 6. Ни одна из них не имеет преимуществ перед другой.

Говорят, что существует 6 равновозможных исходов этого испытания: выпадение очков 1, 2, 3, 4, 5 и 6.

Рассмотрим событие В, которое означает выпадение числа очков, кратного 3. это событие происходит лишь при двух исходах: когда выпало 3 очка и когда выпало 6. эти исходы называют благоприятными исходами события В. Отношение числа благоприятных исходов к числу всех равновозможных исходов равно . Это отношение называют вероятностью события В и пишут: .

Классическим определением вероятности: Вероятностью события называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов.

 - формула Лапласа (формула классической вероятности),

где m_A – благоприятные исходы события А, n – равновозможные исходы.

С помощью формулы Лапласа можно решать задачи на нахождение вероятности события.

Задача

В классе 32 ученика. Двое из них выбраны совсем случайно и посажены за первую парту. Какова вероятность того, что оба они в списке значатся среди первых десяти учеников?

Решение.

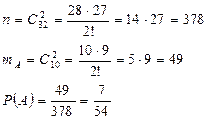
2. Благоприятствующие события. Вероятности событий

В ходе опыта могут возникать более сложные случайные события: например, «выпало четное число очков» при бросании игральной кости. У таких событий тоже есть вероятности.

Обозначим события А, В, С, …

Элементарные события, при которых наступает событие А, называют благоприятствующими событию А.

Пример. Андрей, Борис и Владимир встают в очередь. Всего возможных событий 6: АБВ, АВБ, БАВ, БВА, ВАБ, ВБА. Рассмотрим событие «В стоит первым». Это события ВАБ, ВБА. Значит, данному событию благоприятствуют 2 элементарных события.

Вероятность события равна сумме вероятностей элементарных событий, благоприятствующих этому событию. P(A)=P(a)+P(b)+P(c)+P(d).

Число элементарных событий может быть различным. Вероятности всех элементарных событий неотрицательны и в сумме дают 1. Значит, вероятность любого события А также неотрицательна и в сумме не превосходит 1:

Если Р(А)=0, то событие называется невозможным.

Если Р(А)=1, то событие называется достоверным (ему благоприятствуют все элементарные события).

События, которые имеют одинаковые вероятности, – равновероятные.

Задача

Витя забыл две последние цифры номера телефона приятеля и набрал их наугад. С какой вероятностью этот звонов попадет к приятелю?

 Решение.

Всего возможно 100 исходов (10²), но благоприятный исход только 1. Отсюда, 

1.      Противоположные события. Рассмотрим какое-либо событие А. Ему благоприятствуют некоторые элементарные события. Рассмотрим теперь все прочие элементарные события этого опыта, то есть те, которые не благоприятствуют событию А. Соберем все эти элементарные события вместе. Так мы получим новое событие. Это событие событием, противоположным событию А.

Событием, противоположным событию А, называется событие, которому благоприятствуют все элементарные события, не благоприятствующие событию А.

Событие, противоположное событию А, обозначается . Если событие В противоположно событию А, то есть , то . Поэтому события А и  называются взаимно противоположными или дополнением друг друга.

Пример. Событие А: «при бросании игральной кости выпало 5 или 6 очков».

      Событие : «при бросании игральной кости выпало 1, 2, 3, 4 очка».

Взаимно противоположные события одновременно произойти не могут, но какое-либо из них происходит обязательно. Поэтому .

Сумма вероятностей взаимно противоположных событий равна 1.

Следовательно,  и .

Пример. Какова вероятность того, что при бросании двух игральных костей на них выпадет неодинаковое число очков?

Решение: обозначим описанное событие А. Тогда : «на обеих костях выпало одинаковое число очков».

Событию  благоприятствуют 6 элементарных событий:

(1,1), (2,2), (3,3), (4,4), (5,5), (6,6).

Вероятность каждого из них равна 1/36, следовательно,

.

Значит, .

Решение задач

Докажите, что события А и В не могут быть взаимно противоположными, если:

а) Р(А)=0,7;  Р(В)=0,45;

б) Р(А)=0,3;  Р(В)=0,7.

Решение. а) 0,7+0,45=1,15=> события А и В не могут быть взаимно противоположными;

                 б) 0,3+0,7=1 => события А и В могут быть взаимно противоположными.