
Перестановки. Размещения. Сочетания.
Цель: изучение элементов комбинаторики
Задачи: - познакомить учащихся с элементами комбинаторики;
- учить решать задачи с помощью элементов комбинаторики;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Сообщение темы и цели занятия
В науке и практике часто встречаются задачи, решая которые, приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Решать такие задачи помогает комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составленной по заданным правилам.
Перестановка
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Пример. Сколькими способами можно построить трех человек в шеренгу?
Решение: а в с, а с в, в а с, в с а, с а в, с в а.
Pn –
число перестановок. ![]()
Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке.
![]()
где n! называется факториалом числа n. Это произведение первых натуральных n чисел от 1 до n.
Задача 1. В автосервис приехали 5 машин для ремонта. Сколько существует способов выстроить их в очередь на обслуживание?
Решение: ![]()
Задача 2. Сколько различных последовательностей можно составить из букв слова (необязательно осмысленных)?
а) учебник;
б) автор;
в) фонарь.
Решение: ![]() .
.
![]() .
.
![]() .
.
Размещение
Размещением из n элементов по k ![]() называется
любое множество, состоящее из любых k элементов, взятых в определенном порядке из n элементов.
называется
любое множество, состоящее из любых k элементов, взятых в определенном порядке из n элементов.
![]() .
.
Задача 1. Учащиеся 2 класса изучают 8 предметов. Сколькими способами можно составить расписание на 1 день, чтобы в нем было 4 различных предмета?
Решение: ![]() .
.
Задача 2. Сколькими способами 6 студентов, сдающих экзамен, могут занять место в аудитории, в которой стоит 20 одноместных столов?
Решение: ![]()
Сочетание
Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данныхn элементов.
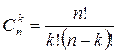
Задача 1. Сколькими способами можно распределить между шестью различными лицами две одинаковые путевки?
Решение: ![]()
Задача 2. В классе 25 учеников. Сколькими способами учитель может выбрать в этом классе для опроса:
а) 5 различных учеников;
б) 6 различных учеников;
в) 20 различных учеников.
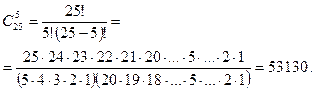 Решение:
Решение:
а)
б) ![]()
в) ![]()
2. Самостоятельная работа
Задача 1
На дверях четырех одинаковых кабинетов надо повесить таблички с фамилиями четырех заместителей директора. Сколькими способами это можно сделать?
Решение: ![]() .
.
Задача 2
Сколькими способами могут быть разделены первая, вторая и третья премии между 15 участниками конкурса?
Решение: ![]() .
.
Задача 3
Иван Николаевич купил билет лото «6 из 49». Он должен зачеркнуть 6 номеров из 49. сколько существует способов это сделать?
Решение: ![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.