Конспект элективного курса по математике "Рассеивание значений"(7 класс)

Рассеивание значений. Дисперсия и стандартное отклонение. Закон больших чисел

Цель: изучение случайных величин

Задачи:- ввести понятия: дисперсия, стандартное отклонение, закон больших чисел;

             - учить вычислять дисперсию, используя ее свойства;

             - учить решать задачи на закон больших чисел;

             - развивать логическое мышление, кругозор, математическую речь, интерес к математике.

Ход занятия

1.     Рассеивание значений. Дисперсия и стандартное отклонение

Вычислим математическое ожидание случайной величины Х:

М(Х)=25.

А теперь вычислим математическое ожидание случайной величины Y:

М(Y)=25.

Любопытно, распределение случайных величин Х и Y разные, а математические ожидания одинаковые. Таблицы показывают, что возможные значения величины Х значительно отличаются от ее среднего значения, равного 25, в то время как значения величины Y близки к среднему значению, то есть значения случайной величины Y компактнее сосредоточены около М(Y), чем значения случайной величины Х около М(Х).

Для измерения сосредоточенности значений случайной величины обычно применяют математическое ожидание случайной величины . Такое математическое ожидание называют дисперсией случайной величины Х и обозначают D(X). Таким образом, .

У дисперсии также есть и недостаток: дисперсия измеряется не в тех единицах, что сама случайная величина. Например, напряжение измеряется в вольтах. Тогда дисперсию придется измерять в квадратных вольтах.

По этой причине вместо дисперсии часто используется мера рассеивания, которая называется средним квадратическим или стандартным отклонением и равна арифметическому квадратному корню из дисперсии, .

Свойства дисперсии

Дисперсия вычисляется по формуле .

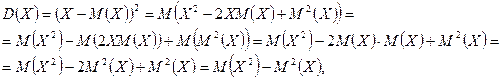
учитывая, что ,  и  - постоянные числа.

Мы получили еще одну формулу дисперсии

.

1)    Дисперсия постоянной величины равна нулю:

.

2) Постоянный множитель можно вынести за знак дисперсии:

D(СХ)=СD(Х).

1)    Дисперсия суммы независимых событий равна сумме их дисперсий:

.

Пример. Найти дисперсию случайной величины, распределенной по биномиальному закону.

Решение. Случайная величина Х, распределенная по биномиальному закону, представляет нам число событий А при n независимых испытаниях, когда вероятность появления событий А есть p, а непоявления q=1-p.

Пусть  - число событий А при i-м испытании.  может принимать два значения: 1 с вероятность p (А произошло) и 0 с вероятность q (А не произошло). Тогда .

Отсюда, .

Так как  - независимые случайные величины, то

.

Задача.

Проводится серия выстрелов по мишени. Вероятность попадания равна p=0,3. Подсчитывается число попаданий S. Найдите дисперсию величины S, если всего произведено:

а) 100 выстрелов;

б) 2500 выстрелов.

 Решение.

а)

б)

2.      Закон больших чисел

Закон больших чисел – название собирательное. Так называют математические теоремы, которые при разных условиях утверждают, что среднее арифметическое, составленное из большого числа случайных слагаемых, мало отличается от математического ожидания этого среднего арифметического. В качестве примера закона больших чисел приведем следующее утверждение.

Пусть  - независимые случайные величины, имеющие одинаковое распределение, и пусть а – общее для всех них математическое ожидание. Тогда при достаточно больших n выполняется равенство . Это приближенное равенство тем точнее, чем больше n.

При больших значениях n дисперсия среднего арифметического, которое тоже является случайной величиной, мала, поэтому эта случайная величина не может сильно отличаться от своего математического ожидания, то есть от а. Чем меньше дисперсия, тем меньше случайный разброс около ожидаемого значения, то есть меньше вероятность большого отклонения от ожидаемого значения. Другими словами, чем больше n, тем меньше значения случайной величины  отличаются от а.

Закон больших чисел позволяет нам вместо математического ожидания с большой точностью использовать средние значения, полученные в результате измерения и наблюдения. Если мы провели достаточно много наблюдений случайной величины, то можем найти среднее арифметическое полученной выборки, то есть среднее выборочное.

Средне выборочное используется как приближенное значение математического ожидания.

Пример. Мы не знаем точно распределение, которому подчиняется размер горошин. Поэтому мы не знаем ожидаемый размер средней горошины. Но мы можем произвести много измерений и найти среднее арифметическое. Возьмем 1000 горошин какого-то определенного сорта, выращенного в определенных условиях. Измерим диаметр каждой горошины с точностью до 0,25 мм и результаты занесем в таблицу:

Среднее арифметическое равно

 (мм).

Полученное среднее значение является оценкой математического ожидания случайной величины «диаметр горошины». При этом мы знаем, что чем больше измерений сделано, тем меньше дисперсия среднего арифметического, а значит, тем точность наших выводов. Таким образом, закон больших чисел дает нам уверенность в том, что диаметр 7,0025 мм очень близок к среднему диаметру всех горошин этого сорта, выращенных в сходных условиях.