МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ  

РОССИЙСКОЙ ФЕДЕРАЦИИ

 

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ  ГОСУДАРСТВЕННЫЙ  ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

 

 

 

КАФЕДРА ИНФОРМАТИКИ И МЕТОДИКИ ПРЕПОДАВАНИЯ МАТЕМАТИКИ

 

 

КОНТРОЛЬ В ОБУЧЕНИИ МАТЕМАТИКЕ УЧАЩИХСЯ ОСНОВНОЙ ШКОЛЫ

 

КУРСОВАЯ РАБОТА

БАКАЛАВРА

по направлению подготовки 44.03.05 «Педагогическое образование»

(с двумя профилями подготовки)

профили «Математика», «Информатика»

Дисциплина «Методика обучения по профилю «Математика»»

 

 

 

 

 

Выполнил: студент

очной формы обучения

4 курса, 1 группы

физико-математического факультета

Меркушова Анастасия Владимировна

 

Научный руководитель: доцент кафедры информатики и методики преподавания математики

Титоренко Светлана Алексеевна

 

 

 

 

 

Воронеж ˗ 2019

Оглавление

Введение. 3

Глава I. Роль и функции контроля и проверки знаний, умений и навыков учащихся по математике. 6

§1.1. Понятие качества образования. 6

§1.2. Функции проверки и оценки знаний учащихся по математике. Принципы контроля. 9

§1.3. Виды контроля знаний, формы и методы контроля знаний по математике. Нормы оценки знаний, умений и навыков по математике в средней школе. 12

Глава II. Методические разработки для осуществления контроля в процессе обучения математике. 22

§2.1. Примеры работ контроля и проверки знаний учащихся 5-6 классов. 22

§2.2. Примеры работ контроля и проверки знаний учащихся 7-8 классов. 29

Список литературы. 34

 

 

                                                       Введение     

 

Особенно важным и довольно тонким моментом в учебно-воспитательном процессе как для ученика, так и для учителя является контроль знаний учащихся. В общепризнанном понимании слова контроль – это систематический учет, проверка успеваемости школьников. Именно контроль гарантирует получение учителем информации о процессе познавательной деятельности учащихся в ходе обучения и является составной частью процесса обучения, и, кроме того, дает возможность в получении информации самими учениками о своих успехах. Контроль знаний учащихся имеет воспитывающее и обучающее значение, а также способствует совершенствованию знаний и умений учащихся, более тщательному изучению основ наук, развитию их общеучебных навыков.

Проблема проверки существует довольно давно, а именно, ровно столько же, сколько и сам процесс обучения. Практически все великие педагоги, психологи и методисты когда-то в своей деятельности ставили для себя данную проблему и искали ее более оптимальное решение. Золотая середина, разрешающая все споры, не найдена и до наших дней. Все учителя по-своему отвечают на следующий вопрос: как использовать контроль в учебном процессе?

Обратившись к Российской педагогической энциклопедии, можно сказать, что в ней нет толкования такого понятия, как «контроль», но есть объяснение понятия «проверка»:

«Проверка знаний, умений и навыков учащихся - процесс выявления и сравнения на том или ином этапе обучения результатов уч. деятельности с требованиями, заданными уч. программами» [14, c.113].

Такое утверждение можно объяснить следующим: по статистике в психолого-педагогической литературе чаще всего используется слово «проверка», а вот среди учителей математики в основном употребляется термин «контроль». Учителя математики употребляют термин «проверка» чаще всего тогда, когда говорят о необходимости проверить написанные учащимися письменные работы. Проверка письменных работ, в свою очередь, осуществляется для того, чтобы проанализировать, насколько был усвоен учащимися учебный материал. Как было написано выше, проверка усвоения знаний учащимися – это и есть контроль. Таким образом, можно сказать, что контроль осуществляется с целью проверки усвоения знаний, а знания, в свою очередь, проверяются для того, чтобы проанализировать эффективность учебного процесса. Учитывая все вышенаписанное, можно говорить о том, чтоـ «контроль» и «проверка» являются синонимами синонимы.

Как отмечают большинство методистов и психологов, контроль имеет огромную роль познавательной деятельности учащихся. Н.Ф.Талызина считала, что отсутствие поэтапного контроля «сильно ухудшает качество протекания усвоения, не позволяет своевременно корректировать его ход».

Такие методисты, педагоги и психологи, как П.И. Пидкасистый, И.Я. Лернер, Ю.М. Колягин, М.Н. Скаткин, Н.И. Махмутов, Л.М. Фридман и многие другие уделяют  и уделяли огромное внимание в своих работах проблеме контроля знаний учащихся.

Каждый учитель обязан понимать конкретные трудности, возникающие у ребенка для того, чтобы правильно организовать его работу. Однако, в данный момент времени существует и еще не решена проблема противоречия между однообразием форм и методов контроля и огромным разнообразием  склонностей и индивидуальных особенностей ребенка. Именно поэтому тема данной курсовой работы является актуальной.

Объект исследования: контроль знаний учащихся.

Предмет исследования: контроль в обучении математике.

Цель работы: изучить такое понятие, как контроль в обучении математике и его влияние на усвоение знаний учащимися.

В соответствии с целью были поставлены следующие задачи:

1)    Проанализировать материал по данной теме в учебных и научных источниках;

2)    Изучить понятие качества образования;

3)    Рассмотреть функции проверки и оценки знаний учащихся;

4)    Проанализировать виды, формы контроля в обучении математики

5)    Изучить нормы оценки знаний, умений и навыков по математике;

6)    Рассмотреть использование компонентов учебно-методического комплекта для организации текущего и тематического контроля;

7)    Проанализировать изученную литературу;

8)    Систематизировать и изложить материал в форме курсовой работы.

Основное содержание курсовой работы описано в 2 главах и, соответственно, в 5 параграфах, в которых приведены основные понятия и утверждения,  которые касаются контроля в обучении математике.

 

Глава I. Роль и функции контроля и проверки знаний, умений и навыков учащихся по математике

§1.1. Понятие качества образования

 

Исходя из понятий «качество» и «образование», можно понять, что качество образования рассматривается как педагогическая, экономическая и социальная  категория. Определение «качество образования» в методологическом аспекте является характеристикой образовательного процесса и результата, имеющей значение не только в системе образования, но и в развитии общества в целом. В этой связи понятие «качество образования» можно определить как сложное образование с учетом всех субъективных и объективных характеристик [6, c.54].

Совокупность показателей образовательного учреждения определяется как качество образования у С.Е. Шишова и В.А. Кальнея.

В своей работе А.С. Запесоцкий рассматривает качество образования так:

Результат, где качество образования – это система знаний, умений и навыков специалиста, которые востребованы в профессиональной среде и в обществе целом.

Процесс, в котором качество образования – совокупность свойств и характеристик образовательного процесса, обеспечивающих его способность удовлетворять потребности не только граждан, но и организации, общества и государства [6, c.56].

Как соотношение результата и цели, меру достижения целей, заданных операционально и спрогнозированных в зоне потенциального развития ученика определяет качество образования М.М. Поташник [6, c.58] .

Как свойство, способное удовлетворить запросы потребителей разных уровней определяют качество образования Г.А. Бордовский, А.А. Нестеров, С.Ю. Трапицын [6, c.59].

Л.Н. Давыдова, в свою очередь, предлагает рассматривать качество образования как совокупность характеристик образовательного процесса, которые включают в себя реализацию его целей, условия, которые необходимы для достижения положительных результатов и современные технологии [6, c.60].

Понятие «качество образования» можно рассматривать, как совокупность множества составляющих, из которых наиболее значимыми являются те свойства, которые определяют уровень знаний, умений, навыков, а также компетенций обучаемых и уровень развития их личностных свойств. Если рассматривать на государственном уровне, то  качество образования – это соответствие принятой образовательной доктрины социальным требованиям и нормам, то есть стандартам [7, c.13].

В.П. Панасюк в качестве образования выделяет следующие составляющие:

1) Процессуальный. К нему относится психолого-педагогическая, методическая подготовка преподавателей, а так же административно-организационная структура образовательного учреждения, образовательная программа, учебные программы и планы, материально-техническая база и прочее;

2) Результирующий. К нему относится образованность, состоящая из следующих блоков: информационного, культурологического, ценностно-мотивационного, ресурсного.

Данная точка зрения характеризуется тем, что процессуальное составляющее качество образования содержит в себе качество процесса и качество условий, что указывает на их более тесные взаимосвязи [11, c.400].

А.Е. Бахмутский в качество образования включает следующее:

● уровень учебных достижений учеников;

● уровень развития мышления учеников;

● мотивация к обучению;

● психологическая комфортность образовательного процесса;

● качество содержания используемых образовательных программ;

● качество реализации образовательных программ.

При этом,  понятие «качество образования» постоянно и непрерывно обновляется во взаимосвязи с социальными изменениями.

Для оценки качества образования М.М. Поташник рассматривает в основном качество результатов, элементами которого являются:

● знания, умения, навыки;

● показатели личностного развития;

● отрицательные последствия образования;

● изменение профессиональной компетентности учителя и его отношение к работе [13, c.90].

§1.2. Функции проверки и оценки знаний учащихся по математике. Принципы контроля

 

Обнаружение и достижение успехов учащихся, а так же направление углубления знаний с тем, чтобы создавались условия для последующего включения учащихся в активную учебную деятельность – это и есть основная цель контроля знаний.

Данная цель в первую очередь связана с диагностикой качества усвоения учащимися учебного материала, предусмотренного программой по математике. Кроме того, данная цель связана также с обучением учащихся приемам самоконтроля, взаимоконтроля, формированием потребности в самоконтроле и взаимоконтроле. Так же необходимо заметить, что цель предполагает воспитание у учащихся ответственности за проделанную работу [15, c.218].

Контроль в математике особенно должен быть регулярным, целенаправленным, объективным, всесторонним и индивидуальным. Раскроем эти принципы контроля подробнее:

а) Целенаправленность – предполагает четкое определение цели каждой проверки.

б) Объективность контроля – предупреждает случаи ошибочных и субъективных суждений, которые снижают воспитательное значение контроля и искажают действительную успеваемость учащихся.

в) Всесторонность контроля  - охват большого по содержанию проверяемого материала.

г) Регулярность – систематический контроль, который сочетается с самим учебным процессом.

д) Индивидуальность контроля – требует оценки знаний, умений и навыков каждого ученика [14, c.139].

Если перечисленные цели контроля знаний и умений учащихся реализовать, то в таком случае можно говорить о том, что контроль в обучении математике выполняет функции: обучающую, контролирующую, прогностическую, диагностическую, воспитывающую, развивающую, функцию управления и ориентирующую.

В выявлении состояния знаний и умений учащихся в области математики, степени усвоения приемов познавательной деятельности, навыков рационального учебного труда состоит контролирующая функция [14, c.109].

Обучающая функция, в свою очередь,  заключается в совершенствовании знаний и умений, их систематизации.

Диагностическая функция заключается в получении информации об ошибках, недочетах и пробелах в знаниях учащихся и порождающих их причинах.

Прогностическая функция контроля служит опережающей информацией об учебно-воспитательном процессе. В результате такого контроля получают основания для прогноза о ходе определенного отрезка процесса обучения.

Развивающая функция заключается в стимулировании познавательной активности учащихся, а также в развитии их творческих сил и способностей для более глубокого изучения предмета «математика» [14, c.110].

Ориентирующая функция  – получение информации о степени достижения цели обучения отдельным учеником и классом в целом.

Воспитывающая функция заключается в воспитании у учащихся ответственного отношения к учению, побуждает контролировать себя при выполнении заданий [14, c.112].

Функция управления очень важна для развития самоконтроля школьника, его умения анализировать и правильно оценивать свою деятельность, адекватно принимать оценку педагога. Учителю функция управления помогает выявить проблемы и недостатки в организации педагогического процесса, ошибки своей деятельности («что я делаю не так», «что нужно сделать чтобы») и осуществить корректировку учебно-воспитательного процесса. Таким образом, устанавливается обратная связь между педагогом и обучающимся.

Обособление функции контроля отмечает его значимость в процессе обучения, где они проявляются в разной степени и сочетании. Выполнение на практике выделенных функций делает как контроль, так и сам учебный процесс, более продуктивным [5, c.42].

 

§1.3. Виды контроля знаний, формы и методы контроля знаний по математике. Нормы оценки знаний, умений и навыков по математике в средней школе

 

Сегодня существует большое количество форм контроля над качеством обучения и усвоения материала по математике.

В соответствии с формами обучения на практике выделяются три основных формы контроля: фронтальная, индивидуальная, групповая.

Индивидуальный контроль предполагает получение учеником своего задания, которое он должен выполнить без посторонней помощи. Эта форма актуальна в том случае, когда требуется выяснить индивидуальные способности, знания и возможности отдельных учащихся [5, c.15].

Групповой же контроль предполагает временное деление класса на группы. Каждой группе при этом дается проверочное задание. В зависимости от цели контроля группам предлагаются одинаковые задания или индивидуальные. Такую форму организации контроля применяют при повторении с целью систематизации и обобщения учебного материала, при выделении методов и приемов решения задач, при акцентировании внимания учащихся на наиболее рациональных способах выполнения заданий, на лучшем из вариантов доказательства теоремы и т.п. [5, c.16].

Фронтальный контроль предполагает такие задания, которые предлагаются всему классу. В процессе такой проверки можно выяснить правильность понимания учебного материала, а также качество графического, словесного, предметного оформления и степень закрепления материала в памяти [14, c.20].

В современном обучении процесс проверки и контроля знаний является многоцелевым. Данный процесс должен выявить, знают ли учащиеся фактический материал, умеют ли применять свои знания в различных жизненных ситуациях, а так же могут ли осуществлять мыслительные операции, т.е. сравнивать, обобщать факты и делать общие заключения. Именно это и дает возможность получать такие сведения, которые были бы необходимы для успешного управления воспитанием, обучением и развитием учащихся.

Таким образом, различают три типа контроля:

1.     Внешний, который осуществляется учителем над деятельностью ученика;

2.     Взаимоконтроль, который осуществляется учеником над деятельностью ученика;

3.     Самоконтроль, который осуществляется учеником над собственной деятельностью.

Самоконтроль является особенно важным в развитии учащихся, потому что именно в этом случае учеником осознается правильность своих действий, обнаружение ошибок, совершенный в ходе работы, анализ данных ошибок и предупреждение их в дальнейшем обучении.

Исходя из вышесказанного, можно применять различные формы и методы контроля и проверки знаний учащихся [9, c.13].

Выявить правильность ответа по содержанию, его самостоятельность, последовательность выводов и суждений, а также степень развития логического мышления и культуру речи учащихся позволяет устный опрос. Такая форма применяется для тематического и текущего учетаـ.

Проверить знания большого числа учеников одновременно и за короткое время позволяет письменный контроль. Такой контроль используется в целях диагностики умения применять знания в учебной практике и может быть осуществим в виде контрольных, диктантов, проверочных и самостоятельных работ, а так же тестов, рефератов [10, c.21].

Математические диктанты  – это довольно распространенная форма контроля знаний. С помощью математического диктанта можно  проверить  знание определений, формулировок, свойств, формул,  теорем, умения  и  навыки  в  их использовании.

Сегодня широкую известность получили тесты. Тест, должен отвечать программе, быть своевременным и при этом  согласовываться с целями и задачами, которые ставит учитель в конкретном случае, то есть быть результативным.

Так же в рамках контроля и оценки знаний учащихся по математике может быть проведен зачет. Зачет предназначен для определения достижения конечных результатов обучения по определенной теме каждым учащимся. Перед тем, как начать изучение материала учащиеся знакомятся с перечнем вопросов и обязательных задач по теме, а также дополнительными вопросами и задачами. Необходимость данного контроля обусловлена тем, что для каждого ученика характерен определенный темп овладения учебным материалом [1, c.116].

Зачеты могут быть как письменными, так и устными. На устных зачетах школьники учатся общаться друг с другом, то есть происходит работа в группах, с учителем, могут лучше овладеть диалогической и монологической речью, умением вступать в диалог, участвовать в нем, аргументировать свою точку зрения [1, c.117].

После изучения нескольких связанных между собой тем, классу предлагаются вопросы к зачету, около 10 - 15 вопросов. Затем, спустя 3-4 дня проводится опрос учителем по любым пяти вопросам.

Опрос  является методом сбора первичной информации со слов опрашиваемого. Он часто используются для оперативной проверки уровня готовности к восприятию следующего нового материала, а также для акти­визации внимания. Опрос может проводиться чаще всего либо в начале урока, либо в конце для закрепления новых понятий и терминов. Элементами опроса пользуются и во время проведения зачета [12, c.201].

Дискуссия является методом активного обучения, который основан на публичном обсуждении проблемы, цель которого выяснение и сопоставление различных точек зрения, нахождение правильного решения спорного вопроса.

Дискуссия может быть организована как в устной, так и в письменной форме и использует сочетание методов собеседования, опроса и наблюдения. Главное условие проведения дискуссии – наличие достаточного объема информации по обсуждаемой проблеме [12, c.202].

Так же существует большое количество нестандартных форм контроля знаний обучающихся:

1.     Математическая эстафетаـ. Такой вид контроля чаще всего эффективен при проверке умений пользоваться формулами, решать несложные задачи.

2.     Математическая викторина. Она может быть использована на любом уроке математики для повторения изученного материалаـ. Она позволяет активизировать деятельность учащихся, прививать им интерес к предмету. Так же можно проводить викторину для групп учащихся или индивидуально для каждого ученика [15, c.110].

Так как произошло увеличение умственной нагрузки на уроках математики, учителям необходимо задуматься над тем, как поддержать интерес к изучаемому предмету и активность учеников на протяжении всего урока. Важная роль здесь отводится дидактическим играм – это современный метод обучения и воспитания, образовательной, воспитывающей и развивающей функциями, действующими в единстве. Дидактическая игра – это средство обучения и воспитания. Это такой вид творческой деятельности, который тесно связан с другими видами учебной работы. К дидактическим играм, которые могут использоваться на уроках математики для контроля знаний, можно отнести:

1.     Кроссворд;

2.     Математическое лото;

3.     Математические турниры.

Учебная деятельность учащихся включает в себя контрольно-оценочную, которая подразумевает контроль учебной работы во всех видах и на всех этапах урокаـ, оценку результатов работы учащихся, их учет и корректировку [1, c.79].

К основным целям контрольно-оценочной деятельности можно отнести следующие:

1.     Активизация учебно-познавательной деятельности каждого ребёнка;

2.     Побуждение учащихся к взаимообучению;

3.     Побуждение учащихся к самостоятельной работе во внеурочное время;

4.     Самооценка уровня усвоения материалаـ.

Однако, учителю необходимо заботиться о накопляемости отметок, о необходимости оценки знаний, умений и навыков по математике отдельных учащихся, добиваться активного включения учащихся в учебно-познавательную деятельность [9, c.29].

Рассмотрим теперь нормы оценки знаний, умений и навыков по математике в средней школе.

Учителю важно знать, как соотнести фактические знания ученика и оценку, отражающую эти знания.

Оценка знаний – систематический процесс, который состоит в определении степени соответствия имеющихся знаний, умений, навыков, предварительно планируемым [5, c.97].

Примерные нормы представляют основу, исходя из которой, учитель оценивает знания и умения учащихся.

Содержание и объем материала, подлежащего проверке и оценке, определяются программой по математике для средней школы. В задания для проверки включаются основные, типичные и притом различной сложности вопросы, соответствующие проверяемому разделу программы.

При проверке знаний и умений, учащихся учитель выявляет не только степень усвоения учащимися теории и умения применять ее на практике, но также умение самостоятельно мыслить [15, c.56].

Основными формами проверки знаний и умений учащихся по математике в средней школе являются: устный опрос и письменная контрольная работа, наряду с которыми применяются и другие формы проверки. При этом учитывается, что в некоторых случаях только устный опрос может дать более полные представления о знаниях и умениях учащихся; в тоже время письменная контрольная работа позволяет оценить умение учащихся излагать свои мысли на бумаге; навыки грамотного и фактически грамотного оформления выполняемых ими заданий [6, c.160].

При оценке устных ответов и письменных контрольных работ учитель в первую очередь учитывает имеющиеся у учащегося фактические знания и умения, их полноту, прочность, умение применять на практике в различных ситуациях. Результат оценки зависит также от наличия и характера погрешностей, допущенных при устном ответе или письменной контрольной работе [6, c.161].

Среди погрешностей выделяются ошибки, недочеты и мелкие погрешности.

Погрешность считается ошибкой, если она свидетельствует о том, что ученик не овладел основными знаниями, умениями и их применением.

К недочетам относятся погрешности, свидетельствующие о недостаточно полном или недостаточно прочном усвоении основных знаний и умений или об отсутствии знаний, не считающихся в соответствии с программой основными. К недочетам относятся погрешности, объясняющиеся рассеянностью или недосмотром, но которые не привели к искажению смысла полученного учеником задания или способа его выполнения. Грамматическая ошибка, допущенная в написании известного учащемуся математического термина, небрежная запись, небрежное выполнение чертежа считаются недочетом [7, c.40].

К мелким погрешностям относятся погрешности в устной и письменной речи, не искажающие смысла ответа или решения, случайные описки и т. п.

Граница между ошибками и недочетами является в некоторой степени условной. В одно время при одних обстоятельствах допущенная учащимися погрешность может рассматриваться как ошибка, в другое время и при других обстоятельствах она может рассматриваться как недочет.

Каждое задание для устного опроса или письменной контрольной работы представляет теоретический вопрос или задачу.

         Ответ на вопрос считается безупречным, если его содержание точно соответствует вопросу, включает все необходимые теоретические сведения, обоснованные заключения и поясняющие примеры, а его изложение и оформление отличаются краткостью и аккуратностью [7, c.12].

         Решение задачи считается безупречным, если получен верный ответ при правильном ходе решения, выбран соответствующий задаче способ решения, правильно выполнены необходимые вычисления и преобразования, последовательно и аккуратно оформлено решение.

Оценка ответа учащегося при устном опросе и оценка письменной контрольной работы проводится по пятибалльной системе [7, c.13].

         Как за устный ответ, так и за письменную контрольную работу может быть выставлена одна из отметок:5,4,3,2,1.

Оценка устных ответов.

Ответ оценивается отметкой «5», если учащийся:

         1) полностью раскрыл содержание материала в объеме, предусмотренном программой и учебником;

         2) изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

         3) правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

         4) показал умение иллюстрировать теорию конкретными примерами, применять в новой ситуации при выполнении практического задания;

         5) продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при ответе умений и навыков;

         6) отвечая самостоятельно, без наводящих вопросов учителя [5, c.17].

         Возможны 1-2 неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку “5”, но при этом имеет один из недочетов:

         1) в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

         2) допущены 1-2 недочета при освещении основного содержания ответа, исправленные после замечания учителя;

         3) допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя [5, c.18].

Ответ оценивается отметкой «3», если:

         1) неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программы;

         2) имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

         3) ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил обязательное задание [5, c.19].

Ответ оценивается отметкой «2», если:

         1) не раскрыто содержание учебного материала;

         2) обнаружено незнание или не понимание учеником большей или наиболее важной части учебного материала;

         3) допущены ошибки в определении понятия, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя [5, c.21].

Оценивание письменных контрольных работ.

         При проверке письменных работ по математике следует различать грубые и негрубые ошибки.

         К грубым ошибкам относятся:

·        вычислительные ошибки в примерах и задачах;

·        ошибки на незнание порядка выполнения арифметических действий;

·        неправильное решение задачи (пропуск действий, неправильный выбор действий, лишнее действие);

·        недоведение до конца решения задачи или примера;

·        невыполненное задание [11, c.312].

         К негрубым ошибкам относятся:

·        нерациональные приемы вычислений;

·        неправильная постановка вопроса к действию при решении задачи;

·        неверно сформулированный ответ задачи;

·        неправильное списывание данных чисел, знаков;

·        недоведение до конца преобразований [11, c.313].

         При оценке работ, включающих в себя проверку вычислительных навыков, ставятся следующие отметки:

«5» - работа выполнена безошибочно;

«4» - в работе допущены 1 грубая и 1-2 негрубые ошибки;

«3» - в работе допущены 2-3 грубые или 3 и более негрубые ошибки;

«2» - если в работе допущены 4 и более грубых ошибок.

          При оценке работ, состоящих только из задач, ставятся следующие отметки:

«5» - если задачи решены без ошибок;

«4» - если допущены 1-2 негрубые ошибки;

«3» - если допущены 1 грубая и 3-4 негрубые ошибки;

«2» - если допущено 2 и более грубых ошибок.

Учитель может повысить отметку за оригинальный ответ или оригинальное решение, которые свидетельствуют о высоком математическом развитии учащегося, а так же за решение более сложной задачи или ответа на наиболее трудный вопрос, предложенные сверх обычных заданий.

         Оценивая ответ учащегося или письменную контрольную работу, учитель дает устно качественную характеристику их выполнения [6, c.38].

Оценивание решения одной задачи, одного примера, ответа на один вопрос.

         Это необходимо, т. к. при устном опросе почти всегда дается один вопрос, у доски, да часто и самостоятельно в классе учащиеся решают одну задачу. К тому же умение оценивать решение одной задачи облегчает оценку комплексного задания [6, c.39].

         Решение задачи обычно состоит из нескольких этапов:

         а) осмысление условия и цели задачи;

         б) возникновение плана решения;

         в) осуществление намеченного плана;

         г) проверка полученного результата.

         Оценивая выполненную работу, естественно учитывать результаты деятельности учащегося на каждом этапе; правильность высказанной идеи, плана решения, а так же степень осуществления этого плана при выставлении оценки нужно считать решающими. Таким образом, при оценке решения задачи необходимо учитывать, насколько правильно учащийся понял ее, высказал ли он плодотворную идею и как осуществил намеченный план решения, какие навыки и умения показал, какие использовал знания [7, c.40].

         При устном ответе по теоретическому материалу решающим является умение рассуждать, аргументировать, применять ранее изученный материал в доказательствах, видеть связи между понятиями, а так же уметь грамотно и стройно излагать свои мысли.

 

Глава II. Методические разработки для осуществления контроля в процессе обучения математике

§2.1. Примеры работ контроля и проверки знаний учащихся 5-6 классов

 

5 класс:

1.     Математический диктант по теме «Обозначение натуральных чисел»:

·        Записать цифрами число тринадцать тысяч четыреста семь.

·        Записать цифрами число два миллиона.

·        Записать цифрами число пятьдесят семь миллиардов восемь миллионов семьсот тысяч тридцать.

·        Записать самое маленькое натуральное число.

·        Записать самое большое трехзначное число.

·        Число 0 – натуральное?

2.     Устный опрос по теме «Натуральные числа»:

·        Какие числа применяются для счета предметов?

·        Назовите первые шестнадцать чисел натурального ряда.

·        Назовите разряды в классе единиц.

·        Назовите по порядку первые 4 класса в записи натуральных чисел.

·        Как читают многозначные числа?

3.     Самостоятельная работа на тему «Сложение и вычитание дробей с одинаковыми знаменателями»:

Вариант 1:

1.     Закончите правило: Чтобы сложить дроби с одинаковыми знаменателями, надо…

2.     Вычислите:

а)                              б)                                 в)  

3.     Найдите разность:

а)                                б)                                     в)                                                              

Вариант 2:

1.     Закончите правило: Чтобы выполнить вычитание дробей с одинаковыми знаменателями, надо…

2.     Вычислите:

а)                                 б)                                   в)

3.     Найдите разность:

а)                                б)                                     в)                                                              

4.     Контрольная работа по теме «Натуральные числа и их обозначения»:

Вариант 1:

1.     Представьте эти выражения в числовом виде:

а) восемь миллионов шестьсот два.

б) на единицу больше, чем триста три миллиона пятьсот тысяч девять [2, c.153].

2.     Постройте луч CD и на нем нарисуйте отрезок AB. Длина отрезка AB составляет 4 см 4 мм, а длина отрезка СB – 9 см 7 мм. Чему равна длина отрезка CА?

3.     Нарисуйте луч AB, прямую CD и четырехугольник EFGH так, чтобы:

а) луч AB пресекал отрезок FG;

б) прямая CD пересекала отрезки EF и FG.

4.     Напишите двузначные числа, у которых число десятков на две единицы больше, чем число единиц.

 

Вариант 2:

1.     Представьте эти выражения в числовом виде:

а) семь миллиардов восемнадцать миллионов триста пять.

б) на единицу меньше, чем восемьсот две тысячи пятьсот.

2.     Постройте луч CD и на нем нарисуйте отрезок AB. Длина отрезка AB составляет 5 см 2 мм, а длина отрезка СВ – 13 см 4 мм. Чему равна длина отрезка CА?

3.     Нарисуйте луч AB, прямую CD и четырехугольник EFGH так, чтобы:

а) луч AB пресекал отрезок EF;

б) прямая CD пересекала луч АВ и отрезок EF и GH.

4.     Напишите двузначные числа, у которых число десятков на три единицы больше, чем число единиц.

6 класс:

1.   Контрольная работа «Делимость чисел, делители и кратные», «Признаки делимости», «Простые и составные числа», «НОД и НОК».

Вариант 1:

1. Задано число 132. Найдите все его делители.

2.   Разложите число 118 на простые множители.

3.   Найдите НОК.

а) 32 и 24; б) 17 и 51.

4.   Найдите НОД.

а) 26 и 58; б) 72 и 16.

5.   Решите пример и найдите все делители для полученного числа:

6.   Найдите максимальное трехзначное число, которое кратно числам 3, 5 и  12 [3, c.55].

Вариант 2:

1.     Задано число 156. Найдите все его делители.

2.     Разложите число 224 на простые множители.

3.     Найдите НОК.

а) 16 и 22;

б) 24, 8 и 16.

4.     Найдите НОД.

а) 42 и 124;

б) 58 и 28.

5.     Решите пример и найдите все делители для полученного числа:

6.     Найдите максимальное трехзначное число, которое кратно числам 5, 10 и 12?

1.     Тест «Отношения и пропорции», «Прямая и обратная пропорциональные зависимости»

1.     Найдите отношения чисел 13,5 к 3. Выберите правильный ответ:

А) 2,9; Б) ; В) 4,5; Г) .

2.     Выразите отношение 36: 42 обыкновенной дробью.

А) ;  Б) ; В) ; Г) .

3.     Решите уравнения и впишите ответы________________

А) ; Б) .

3. Билеты для устного экзамена:

Билет 1

Отношение. Деление в данном отношении.

Сложение отрицательных чисел. Определение и примеры

Решение задачи на составление уравнения.

Билет 2

Пропорция, основное свойство пропорции.

Перпендикулярные прямые. Определение и примеры.

Решение уравнения.

Билет 3

Противоположные числа. Рациональные числа.

Параллельные прямые. Определение и примеры

Решение задачи по теме «Пропорции»

Билет 4

Координатная плоскость.

Сложение чисел с разными знаками. Определение и примеры

Решение задачи по теме «Масштаб»

Билет 5

Модуль числа.

Умножение рациональных чисел. Определение и примеры

Решение примеров на действия с рациональными числами.

Билет 6

Сравнение рациональных чисел.

Графики. Определение и примеры

Решение примера по теме «Раскрытие скобок»

Билет 7

Линейное уравнение с одной переменной.

Приведение подобных слагаемых. Определение и примеры

Решение сложного уравнения.

Билет 8

Числовые неравенства и их свойства.

Деление рациональных чисел. Определение и примеры

Решение уравнения пропорции.

Билет 9

Числовые промежутки.

Масштаб. Определение

Решение задачи на составление пропорции.

 

Билет 10

Прямоугольная система координат.

Осевая симметрия.

Решение задачи по теме « Масштаб»

Билет 11

Длина окружности. Площадь круга. Шар.

Вычитание рациональных чисел. Определение и примеры

Решение примеров на действия с положительными и отрицательными числами.

Билет 12

Понятие функции.

Смежные углы. Определение и примеры

Решение задачи по теме «Окружность»

Билет 13

Линейная функция и её график.

Раскрытие скобок. Определение и пример

Упрощение выражений.

Билет 14

Частные случаи линейной функции.

Рациональные числа. Определение и примеры

Задачи на определение длины окружности.

Билет 15.

Взаимное расположение графиков линейных функций.

Координаты на прямой. Определение и примеры

Решение системы уравнений с двумя переменными (метод сложения).

Билет 16

Линейное уравнение с двумя переменными.

Расстояние от точки до прямой.

Решение системы уравнений с двумя переменными (метод подстановки)

 

Билет 17

Системы линейных уравнений с двумя переменными.

Вертикальные углы. Определение и примеры

Координатная плоскость: построение точек с указанными координатами и нахождение координат указанных точек.

Билет 18

Линейное уравнение с одной переменной и его свойства.

Прямо пропорциональные величины. Определение и примеры.

Уравнение с модулем.

Билет 19

Числовые промежутки.

Правила раскрытия скобок. Определение и примеры.

Решение уравнения.

Билет 20

Координатная прямая.

Длина окружности. Площадь круга.

Решение системы неравенств с одной переменной.

§2.2. Примеры работ контроля и проверки знаний учащихся 7-8 классов

 

7 класс:

1.     Математический диктант на тему «Выражения»:

1. Запишите пример числового выражения.

2.     Найдите значения выражения: 

3.     Запишите в виде выражения: сумма числа 7 и частного чисел 30 и 5.

4.     Запишите в виде выражения: квадрат числа х.

5.     Найдите значение выражения: 5a-8? Если a = -2.

6.     Напишите формулу четного числа.

7.     При каких значения переменной не имеет смысла выражение: .

8.     Напишите пример строгого неравенства.

9.     Запишите в виде неравенства: y – неотрицательное число.

10.  Запишите в виде двойного неравенства: 0,47 больше 0,4 и меньше 0,5.

11.  Как читается знак «≥».

12.  Сравните х+3 и 3х, при х = 2.

2.     Устные упражнения по алгебре на тему «Уравнения»:

1.     Подберите такое значение а, при котором уравнение ах=-3 имеет:

a)     положительный корень;

b)    отрицательный корень;

c)     не имеет корней; (а=0.)

d)    можно ли подобрать такое значение а, при котором данное

уравнение имеет бесконечное множество корней?

2.     Решите уравнение: 3х-1,5=3х+2; 3х+1=2х+1.

3.     Решите уравнение:

a)     х(х-25)=0;

b)    (х+4)(х-7)=0;

c)     (х+1)(2+х)(х+3)=0;

d)    (х-2)(2х-7)(3х+3)=0;

e)     (х+5)(х²+1)=0.

4.     Является ли решением уравнения у(х-2)=0 пара чисел (3;8); (2;7); (2;-1); (3;0). Найдите еще несколько решений.

5.     При каких значениях переменных а и в верно равенство ав=0:

a)     3 и 1;

b)    0 и -19;

c)     5 и -5;

d)    17 и 0;

e)     0 и 0.

6.     Решите уравнение: а(а-2)+3(а-2)=0.

3.     Самостоятельная работа по теме «Прямоугольная система координат на плоскости:

1.     Постройте в координатной плоскости прямую, проходящую через точки С(-4;3) и Е(3;-1). Найдите координаты точек, в которых эта прямая пересекает ось Ох и ось Оу.

2.     Постройте в координатной плоскости точки:

А(3,5; 4), В(0; 6), С(-3,5; 4), Е(-3,5; -4), К(0;-6), М(3,5; -4).

Соедините эти точки последовательно отрезками так, чтобы получился многоугольник. Запишите координаты точек пересечения с осью Ox прямых СЕ и АМ.

8 класс:

1.     Контрольная работа по алгебре на тему: «Умножение дробей. Возведение дроби в степень»:

1.     Выполните умножение:

  .

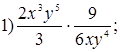
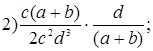
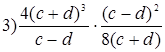2.     Выполните возведение в степень:

   

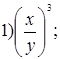
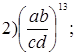
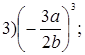
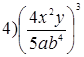
3.     Выполните деление:

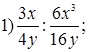
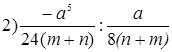 ;  4)

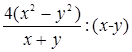
4.     Постройте график функции

и найдите значение функции, соответствующее значению аргумента, равному -2.

5.   Определите принадлежит ли графику функции  точка A(-2,1).

2.     Математический диктант по геометрии на тему «Многоугольники»:

Инструкция: Учащимся будут продиктован ряд утверждений, касающихся темы «Многоугольники».  Если ученик согласен с услышанным утверждением, ставит в бланке ответов «+», иначе «-».

1.   У многоугольника стороны могут пересекаться, а могут не пересекаться.

2.   Смежные отрезки многоугольника лежат на одной прямой.

3.   Две смежные стороны многоугольника имеют одну общую вершину.

4.   Название многоугольника зависит от количества вершин.

5.   Количество сторон многоугольника не зависит от количества его вершин.

6.   Периметр многоугольника – это сумма длин всех его сторон.

7.   Соседние вершины многоугольника лежат на разных сторонах.

8.   Отрезок, соединяющий любые две соседние вершины, называют диагональю многоугольника.

9.   Любой многоугольник разделяет плоскость на внешнюю и внутреннюю области.

10. Невыпуклый многоугольник находится по одну строну от прямой, проходящей через любую его сторону.

11. Четырехугольники бывают только выпуклые.

12. У четырехугольника можно провести четыре диагонали.

13.  Каждая диагональ разбивает четырехугольник на два треугольника.

14.  Сумма углов любого выпуклого четырехугольника, параллелограмма и трапеции равна 360⁰.

15.  У параллелограмма соседние стороны параллельны и равны.

16.  У параллелограмма противоположные углы равны.

17.  Диагонали параллелограмма точкой пересечения не делятся пополам.

18.  У трапеции противоположные стороны параллельны.

19.  Основания трапеции между собой равны.

20.  Боковые стороны равнобедренной трапеции между собой равны.

21.  У прямоугольной трапеции три угла прямые.

3.   Вопросы к зачету по алгебре на тему «Квадратные уравнения»:

1.   Какое уравнение называют квадратным уравнением?

2.   Какое уравнение называют приведённым квадратным уравнением?

3.   Какое уравнение называют неполным квадратным уравнением?

4.   Какие способы решения неполных квадратных уравнений ты знаешь?

5.   Что называют дискриминантом квадратного уравнения? Формула дискриминанта.

6.   Формула корней квадратного уравнения.

7.   Формула корней квадратного уравнения, в котором второй коэффициент является чётным числом.

8.   Особые случаи решения квадратного уравнения. Метод коэффициентов: a + b + c = 0; a + c = b;

9.   Теорема Виета и обратная ей.

10.Решение квадратных уравнений методом «переброски» старшего коэффициента.

 

Заключение

 

Таким образом, подводя итоги курсовой работы можно обобщить следующее: при всех достаточно разнообразных подходах к проблеме контроля и проверки, и по мнениям различных ученых, систематический контроль знаний и умений учащихся является неотъемлемой и очень важной частью успешного обучения школьников, овладения учебным материало, а так же способности к использованию полученной информации в повседневной жизни.

Учителю математики необходимо в своей работе использовать как стандартные методы контроля, так и нетрадиционные. Именно умение учителя владеть правильно различными формами контроля и проверки знаний и способствует повышению уровня заинтересованности уроком школьниками, качества полученных знаний.

Необходимо также отметить, что в данной работе удалось рассмотреть такие понятия, как: качество, качество образования, контроль и проверка знаний, а так же различные формы и методы контроля и проверки знаний непосредственно на уроках математики.

Таким образом, в ходе работы были выполнены все поставленные задачи:

1) Найти материал по данной теме в учебных и научных источниках;

2) Изучить понятие качества образования;

3) Рассмотреть функции проверки и оценки знаний учащихся;

4) Проанализировать виды, формы и методы контроля;

5) Рассмотреть использование компонентов учебно-методического комплекта для организации текущего и тематического контроля;

6) Проанализировать изученную литературу;

7) Систематизировать и изложить материал в форме курсовой работы.

А так же была достигнута цель курсовой работы.

Список литературы

 

1.     Алгебра, 7 класс. Учебник / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков [и др.] ; под редакцией С.А. Теляковского. – М.: Просвещение, 2019. – 256 с.

2.     Алгебра. 8 класс. Учебник. ФГОС / Г.В. Дорофеев, Е.А. Бунимович, Л.В. Кузнецова [и др.] ; под редакцией Л.В. Кузнецовой. – М.: Просвещение, 2019. – 320 с.

3.     Быков А.В. О технологии проведения зачетного урока / А.В. Назаров // Математика в школе. – 2013. - №5. – С. 112-120.

4.     Выговская В.В. Сборник практических задач по математике: 6 класс / В.В. Выговская. – М.: ВАКО, 2012. – 167 с.

5.     Глазков Ю.А. Математика: 5 класс: контрольные измерительные материалы / Ю.А. Глазков. – М.: Экзамен, 2014. – 150 с.

6.     Дорофеев Г.В. Математика. 6 класс. Учебник. В 3 частях. ФГОС / Г.В. Дорофеев, Л.Г. Петерсон. – М.: Ювента, 2019. – 416 с.

7.     Ершова А.П. Самостоятельные и контрольные работы по математике для 5 класса / А.П. Ершова. – М.: ИЛЕКСА, 2010. – 56 с.

8.     Костылев Ф.В. Учить по-новому: Нужны ли оценки-баллы / Ф.В. Костылев. – М.: Владос, 2000. – 104 с.

9.     Лернер И.Я. Качества знаний учащихся. Какими они должны быть? / И.Я. Ларнер. –  М.: Знание, 2013. – 180 с.

10.  Методика преподавания математики в средней школе: Частная методика : учебно-методическое пособие для студентов педагогических институтов и университетов по физико-математической специализации / составитель: В.И.Мишин ; Московский педагогический государственный университет. – Москва, 2014. – 72 с.

11.  Математика. 5 класс.  В 2-х частях. ФГОС / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2017. – 190 с.

12.  Никольский С.М. Математика. 5 класс / С.М. Никольский. – М.: Просвещение, 2015. – 272 с.

13.  Подласый И.П. Педагогика / И.П. Подласый. – М.: Высшее образование, 2008. – 540 c.

14.  Саранцев Г.И. Методика обучения математике в средней школе : учебно-методическое пособие для студентов педагогических институтов и университетов по физико-математической специализации  / Г.И. Саранцев ; Московский педагогический государственный университет – Москва, 2012. – 34 с.

15.  Талызина Н.Ф. Теоретические основы контроля в учебном процессе / Н.Ф. Талызина. – М.: Знание, 2013. – 220 с.

16.  Шевелев А.И. Тематический контроль знаний / А.И. Шевелев // Математика в школе. – 2016. - №3. – С. 218-221.

 

Скачано с www.znanio.ru