Контрольная работа №6 Решение задач с помощью рационального уравнения

У р о к 
Тема урока:Контрольная работа № 6 «Решение задач с помощью дробных рациональных уравнений»

Организационный момент

В а р и а н т  1

1. Решите уравнение:

а) ;                              б)  = 3.

2. Из пункта А в пункт В велосипедист проехал по одной дороге длиной 27 км, а обратно возвращался по другой дороге, которая была короче первой на 7 км. Хотя на обратном пути велосипедист уменьшил скорость на 3 км/ч, он все же на обратный путь затратил времени на 10 минут меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из А в В?

В а р и а н т  2

1. Решите уравнение:

а) ;                          б)  = 2.

2. Катер прошёл 12 км против течения реки и 5 км по течению. При этом он затратил столько времени, сколько ему потребовалось бы, если бы он шёл 18 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 3 км/ч.

Решение вариантов контрольной работы

В а р и а н т  1

1. а) . Общий знаменатель х² – 9.  х² = 12 – х;  х² + х – 12 = 0.

По теореме, обратной теореме Виета, х₁ = 3; х₂ = –4.Если х = 3, то х² – 9 = 0.Если х = –4, то х² – 9 ≠ 0.

б)  = 3. Общий знаменатель х (х – 2).    6х + 5(х – 2) = 3х(х – 2);  6х + 5х – 10 – 3х² + 6х = 0;

    –3х² + 17х – 10 = 0;3х² – 17х + 10 = 0.

D = (–17)² – 4 · 3 · 10 = 289 – 120 = 169, D > 0, 2 корня.x₁ =  = 5;  2/3

Если х = 5, то х (х – 2) ≠ 0.Если х = , то х (х – 2) ≠ 0.О т в е т: а) –4; б) ; 5.

2. Пусть х км/ч – скорость велосипедиста, с которой он ехал из А в В, тогда (х – 3) км/ч – скорость, с которой он ехал обратно. На путь из А в В он затратил  ч, а обратно  ч. Зная, что на обратный путь он затратил на 10 мин ( часа) меньше, составим уравнение:

 –  = . Общий знаменатель 6х (х – 3).

162(х – 3) – 120х – х(х – 3) = 0;

162х – 486 – 120х – х² + 3х = 0;

х² – 45х + 486 = 0.

D = (–45)² – 4 · 486 = 81, D > 0, 2 корня.

x₁ =  = 27;

x₂ =  = 18.

Ни один из корней не обращает знаменатель в нуль, но корень х = 27 не удовлетворяет условию задачи (слишком большая скорость для велосипедиста).

О т в е т: 18 км/ч.

В а р и а н т  2

1. а) 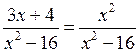. Общий знаменатель х² – 16.

          3х + 4 = х²;

          х² – 3х – 4 = 0.

По теореме, обратной теореме Виета х₁ = 4; х₂ = –1.

Если х = 4, то х² – 16 = 0.

Если х = – 1, то х² – 16 ≠ 0.

б)  = 2. Общий знаменатель х (х – 5).

    3х + 8(х – 5) = 2х(х – 5);

    3х + 8х – 40 – 2х² + 10х = 0;

    –2х² + 21х – 40 = 0;

    2х² – 21х + 40 = 0.

D = (–21)² – 4 · 2 · 40 = 441 – 320 = 121, D > 0, 2 корня.

x₁ =  = 8;

x₂ =  = 2,5.

Если х = 8, то х (х – 5) ≠ 0.

Если х = 2,5, то х (х – 5) ≠ 0.

О т в е т: а) –1; б) 2,5; 8.

2. Пусть х км/ч – собственная скорость катера, тогда против течения он шёл  со  скоростью  (х – 3) км/ч,  по  течению – (х + 3) км/ч  и  по  озеру – х км/ч. Против течения он шёл  ч, по течению  ч, а по озеру он шёл бы  ч. Зная, что на все плавание по реке он затратил бы столько же времени, сколько на плавание по озеру, составим уравнение:

 +  = . Общий знаменатель х (х – 3)(х + 3).

12х(х + 3) + 5х(х – 3) = 18(х – 3)(х + 3);

12х² + 36х + 5х² – 15х – 18х² + 162 = 0;

х² – 21х – 162 = 0.

D = (–21)² – 4 · 162 = 441 + 648 = 1089, D > 0, 2 корня.

x₁ =  = 27;

x₂ =  = –6.

Ни один из корней не обращает знаменатель в нуль, но х = –6 не удовлетворяет условию задачи.

О т в е т: 27 км/ч.

Итог урока.

Задание на дом. Повторить §9.  ОГЭ задание № 20 вариант  5