Контрольная работа по теме применение производной для исследования функции 11 класс

Вариант 1

А1. Исследовать функцию   у = х³- 9х

А2. Найти наибольшее и наименьшее значение функции у = х³- 9х на отрезке [0,5; 2].

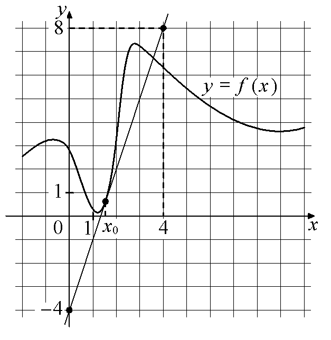
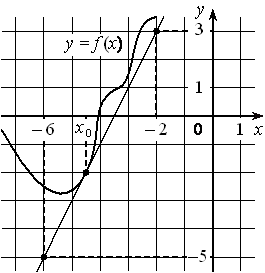
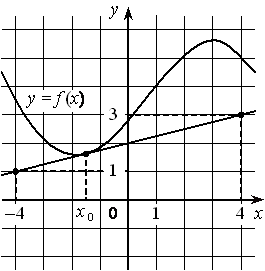
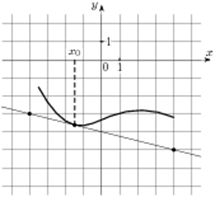
А3. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

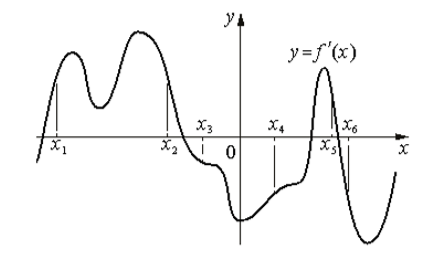
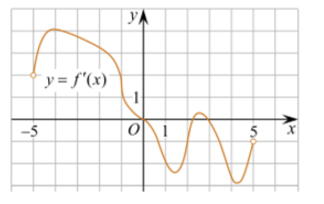
А4  На рисунке изображён график y=f '(x) — производной функции f(x). 
На оси абсцисс отмечены шесть точек: x₁, x₂, x₃, x₄, x₅, x₆. 
Какие из этих точек лежит на промежутках возрастания функции f(x)?

Вариант 1

В1 Исследовать функцию у =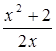      

В2. Найти наибольшее и наименьшее значение функции у = 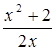      на отрезке [-2; -1]

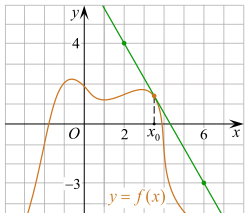
В3 На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

В4 На рисунке изображен график производной функции определенной на интервале Найдите точки максимума функции .

В5 На рисунке изображен график производной функции  определенной на интервале   В какой точке отрезка  принимает наименьшее значение?

Вариант 2.

А1. Исследовать функцию   у = х³ –3х.

А2. Найти наибольшее и наименьшее значение функции у = х³ –3х. на отрезке [-2; 3].

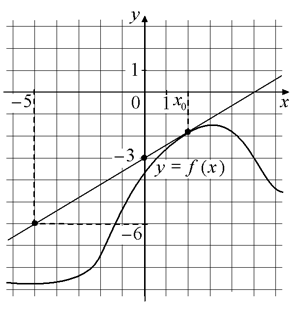
А3. На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

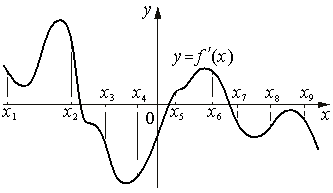
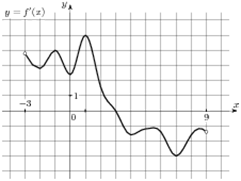
А4 На рисунке изображён график y=f '(x) — производной функции f(x). 
На оси абсцисс отмечены девять точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉. Какие из этих точек лежит на промежутках убывания функции f(x)?

Вариант 2

В1 Исследовать функцию у =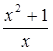   

В2. Найти наибольшее и наименьшее значение функции у = 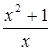  на отрезке [1;2]

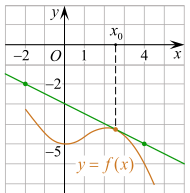
В3 На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

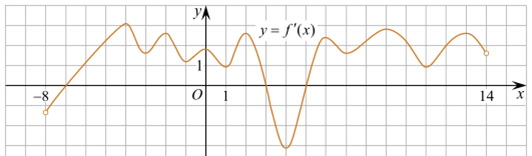
В4 На рисунке изображен график производной функции определенной на интервале   Найдите точки минимума функции .

В5 На рисунке изображен график производной функции  определенной на интервале  В какой точке отрезка  принимает наименьшее значение?

Вариант 3

А1 Исследовать функцию у = 12х² –2х³.

А2 Найти наибольшее и наименьшее значение функции у = 12х² –2х³ на отрезке [-2; 2].

А3 На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x​₀. Найдите значение производной функции f(x) в точке x​₀.

А4

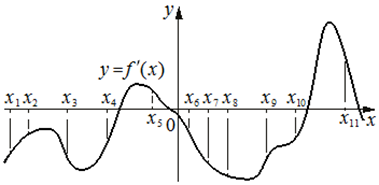
На рисунке изображён график y=f '(x) — производной функции f(x). 
На оси абсцисс отмечено одиннадцать точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁.  Какие из этих точек принадлежит промежуткам убывания функции f(x)?

Вариант 3

В1 Исследовать функцию у =     

В2 Найти наибольшее и наименьшее значение функции у =      на отрезке [-2; -1]

В3 На рисунке изображён график функции y=f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции f(x) в точке x₀.

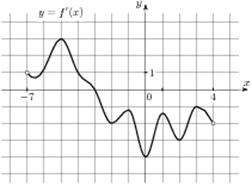
В4 На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите точки минимума функции f(x) на отрезке [−14; 2].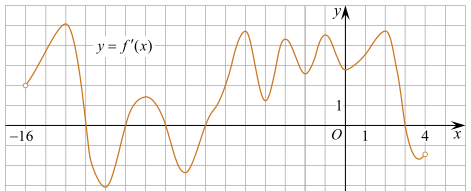

В5 На рисунке изображен график производной функции  определенной на интервале  В какой точке отрезка  принимает наименьшее значение?

Вариант 4

А1 Исследовать функцию f(x) = х³ –6х².

А2 Найти наибольшее и наименьшее значение функции f(x) = х³ –6х² на отрезке [-3; 3].

А3 На рисунке изображены график дифференцируемой функции y=f(x) и касательная к нему в точке с абсциссой x​₀. Найдите значение производной функции f(x) в точке x​₀.

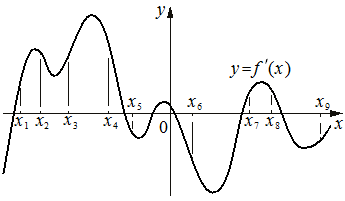
А4 На рисунке изображён график y=f '(x) — производной функции f(x). 

На оси абсцисс отмечено девять точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉. Какие из этих точек принадлежит промежуткам убывания функции f(x)?

Вариант 4

В1 Исследовать функцию у =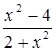  

В2 Найти наибольшее и наименьшее значение функции у = 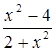 на отрезке [2;3]

В3 На рисунке изображён график функции и касательная к нему

в точке с абсциссой Найдите значение производной функции в точке

В4 На рисунке изображен график производной функции  определенной на интервале  Найдите точки максимума функции на отрезке

В5 На рисунке изображен график производной функции  определенной на интервале  В какой точке отрезка  принимает наименьшее значение?