Контрольная работа. Уравнения регрессии.

Вариант 5

Описать экспериментальный дизайн для проверки гипотезы о нелинейной связи переменных. Для шести выборок вида 3 уровня 1-го фактора; 2 уровня 2-го фактора проверить гипотезу о наличии нелинейной (квадратичной или U-образной) связи с помощью таблиц 3 × 2.

1.                 На нелинейные модели регрессии, которые являются внутренне линейными, т. е. сводимыми к линейному виду, распространяются все методы проверки гипотез, используемые для классических линейных моделей регрессии.

Таким образом, если внутренне линейную модель регрессии можно свести к линейной модели парной регрессии, то на эту модель будут распространяться все методы проверки гипотез, используемые для парной линейной зависимости.

Проверка гипотезы о значимости линейной модели множественной регрессии состоит в проверке гипотезы значимости индекса детерминации R2.

Рассмотрим процесс проверки гипотезы о значимости индекса детерминации.

Основная гипотеза состоит в предположении о незначимости индекса детерминации, т. е.

Н0:R2=0.

Обратная или конкурирующая гипотеза состоит в предположении о значимости индекса детерминации, т. е.

Н1:R2/=0.

Данные гипотезы проверяются с помощью F-критерия Фишера-Снедекора.

Наблюдаемое значение F-критерия (вычисленное на основе выборочных данных) сравнивают со значением F-критерия, которое определяется по таблице распределения Фишера-Снедекора, и называется критическим.

При проверке значимости индекса детерминации критическое значение F-критерия определяется как Fкрит(a;k1;k2), где а – уровень значимости, k1=l-1 и k2=n-l – число степеней свободы, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров.

При проверке основной гипотезы вида Н0:R2=0 наблюдаемое значение F-критерия Фишера-Снедекора рассчитывается по формуле:

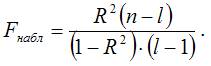
При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) больше критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл›Fкрит, то с вероятностью а основная гипотеза о незначимости индекса детерминации отвергается, и он признаётся значимым. Следовательно, полученная модель регрессии также признаётся значимой.

Если наблюдаемое значение F-критерия (вычисленное по выборочным данным) меньше или равно критического значения F-критерия (определённого по таблице распределения Фишера-Снедекора), т. е. Fнабл=Fкрит, то основная гипотеза о незначимости индекса детерминации принимается, и он признаётся незначимым. Полученная модель регрессии является незначимой и нуждается в дальнейшей доработке.

Если в начале эконометрического моделирования перед исследователем стоит выбор между моделью регрессии, внутренне нелинейной и линейной моделью регрессии (или сводящейся к линейному виду), то предпочтение отдаётся линейным формам моделей.

Проверка предположения о возможной линейной зависимости между исследуемыми переменными осуществляется с помощью коэффициента детерминации r2 и индекса детерминации R2.

Выдвигается основная гипотеза Н0о наличии линейной зависимости между переменными. Альтернативной является гипотеза Н1 о нелинейной зависимости между переменными.

Данные гипотезы проверяются с помощью t-критерия Стьюдента.

Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают с критическим значением t-критерия, которое определяется по таблице распределения Стьюдента.

При проверке гипотезы о линейной зависимости между переменными критическое значение t-критерия определяется как tкрит(а;n-l-1), где а – уровень значимости, n – объём выборочной совокупности, l – число оцениваемых по выборке параметров, (n-l-1) – число степеней свободы, которое определяется по таблице распределений t-критерия Стьюдента.

При проверке основной гипотезы Н0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

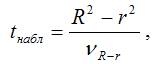
где – величина ошибки разности (R2-r2), которая определяется по формуле:

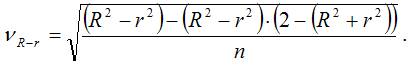
При проверке основной гипотезы возможны следующие ситуации.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. tнабл›tкрит, то с вероятностью а основная гипотеза о линейной зависимости между переменными отвергается. В этом случае построение нелинейной модели регрессии считается целесообразным.

Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. tнабл<=tкрит, то основная гипотеза о линейной зависимости между переменными принимается. Следовательно, взаимосвязь между данными переменными можно аппроксимировать простой линейной формой зависимости.

2.

1) На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит экспоненциальный характер.
Экспоненциальное уравнение регрессии имеет вид y = a e^bx (ln y = ln a + bx + ε)
Здесь ε - случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = a e^bx (ln y = ln a + bx + ε), где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии.
Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x).
Формально критерий МНК можно записать так:
S = ∑(y_i - y^*_i)² → min
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x² = ∑y•x
Для наших данных система уравнений имеет вид
3a + 3 b = 1.79
3 a + 3 b = 1.79
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 0, a = 0.5973
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e^0.59725315e^0x = 1.81712e^0x
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

1. Параметры уравнения регрессии.
Выборочные средние.

2) На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит экспоненциальный характер.
Экспоненциальное уравнение регрессии имеет вид y = a e^bx (ln y = ln a + bx + ε)
Здесь ε - случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения ε_i для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям x_i и y_i можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = a e^bx (ln y = ln a + bx + ε), где e_i – наблюдаемые значения (оценки) ошибок ε_i, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии.
Но только в том случае, если выполняются определенные предпосылки относительно случайного члена (ε) и независимой переменной (x).
Формально критерий МНК можно записать так:
S = ∑(y_i - y^*_i)² → min
Система нормальных уравнений.
a•n + b∑x = ∑y
a∑x + b∑x² = ∑y•x
Для наших данных система уравнений имеет вид
3a + 4 b = 1.39
4 a + 6 b = 2.08
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = 0.3466, a = -0
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e^-0.00000001e^0.3466x = 1e^0.3466x
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)

1. Параметры уравнения регрессии.
Выборочные средние.



Выборочные дисперсии:


Среднеквадратическое отклонение


1.3. Коэффициент эластичности.
Коэффициент эластичности находится по формуле:

E = 1.33ln(0.35) = -1.41
1.4. Ошибка аппроксимации.

Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения регрессии к исходным данным.

1.5. Эмпирическое корреляционное отношение.
Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1].


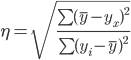
где

Индекс корреляции.
Величина индекса корреляции R находится в границах от 0 до 1. Чем ближе она к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии.


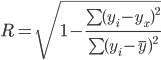
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции:

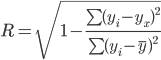
1.6. Индекс детерминации.
Величину R² (равную отношению объясненной уравнением регрессии дисперсии результата у к общей дисперсии у) для нелинейных связей называют индексом детерминации.
Чаще всего, давая интерпретацию индекса детерминации, его выражают в процентах.


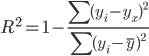
Для оценки качества параметров регрессии построим расчетную таблицу (табл. 2)

2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H₁ ≠ 0, надо вычислить наблюдаемое значение критерия

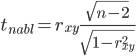
и по таблице критических точек распределения Стьюдента, по заданному уровню значимости α и числу степеней свободы k = n - 2 найти критическую точку t_крит двусторонней критической области. Если t_набл < t_критоснований отвергнуть нулевую гипотезу. Если |t_набл| > t_крит — нулевую гипотезу отвергают.

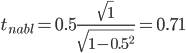
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=1 находим t_крит:
t_крит (n-m-1;α/2) = (1;0.025) = 12.706
где m = 1 - количество объясняющих переменных.
2.2. Интервальная оценка для коэффициента корреляции (доверительный интервал).

r(-5;6)
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:


S²_y = 0.24 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).

S_y = 0.49 - стандартная ошибка оценки (стандартная ошибка регрессии).
S_a - стандартное отклонение случайной величины a.


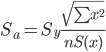
S_b - стандартное отклонение случайной величины b.


2.4. Доверительные интервалы для зависимой переменной.
(a + bx_p ± ε)
где

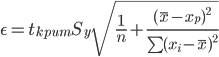
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X_p = 1

Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx_i ± ε)
где


t_крит (n-m-1;α/2) = (1;0.025) = 12.706
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
t_крит (n-m-1;α/2) = (1;0.025) = 12.706




Доверительный интервал для коэффициентов уравнения регрессии.
(b - t_крит S_b; b + t_крит S_b)
(a - t_крит S_a; a + t_крит S_a)
2) F-статистика. Критерий Фишера.



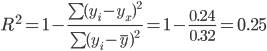
Табличное значение критерия со степенями свободы k₁=1 и k₂=1, F_табл = 161