
Министерство общего и профессионального образования
Ростовской области
государственное бюджетное профессиональное образовательное
учреждение Ростовской области
«Новошахтинский технологический техникум»
(ГБПОУ РО «НТТ»)
КОНТРОЛЬНО-ОЦЕНОЧНЫЕ МАТЕРИАЛЫ
для проведения процедуры оценки уровня освоения обучающимися
ФГОС СПО по ЕН.01 Математика
специальность 22.02.06 Сварочное производство
г. Новошахтинск
РАССМОТРЕНО на заседании Методического объединения «Общеобразовательный цикл» Протокол № __ от__________ Председатель МО __________ Н.А.Тарасюк |
СОГЛАСОВАНО на заседании Методического Совета Протокол № __ от__________ Председатель МС ________ И.Ю.Волкова |
Контрольно-оценочные материалы для проведения процедуры оценки уровня освоения обучающимися федерального государственного образовательного стандарта среднего общего образования, федерального государственного образовательного стандарта среднего профессионального образования по специальности 22.02.06 Сварочное производство и рабочей программы ЕН.01 Математика.
Организация - разработчик: государственное бюджетное профессиональное образовательное учреждение Ростовской области «Новошахтинский технологический техникум»
Разработчик: Тарасюк Н.А. - преподаватель государственного бюджетного профессионального образовательного учреждения Ростовской области «Новошахтинский технологический техникум»
СОДЕРЖАНИЕ
1. Спецификация комплекта оценочных материалов по ОПОП:
1.1. Назначение комплекта оценочных материалов.
1.2. Общее количество тестовых заданий.
1.3. Распределение тестовых заданий по компетенциям и дисциплинам.
1.4. Типы, уровень сложности и время выполнения тестовых
заданий.
1.5. Система оценивания выполнения тестовых заданий.
1.6. Описание дополнительных материалов и оборудования, необходимых для выполнения тестовых заданий (при необходимости).
1.7. Продолжительность выполнения
1.8. Сценарий выполнения тестовых заданий
2. Тестовые задания
3. Ключи к оцениванию тестовых заданий
1. Спецификация комплекта оценочных материалов
1.1. Назначение комплекта оценочных материалов
Контрольно-оценочные материалы (далее – КОМ) подготовлены с целью оценки результатов освоения программы подготовки специалистов среднего звена
- УГС 22.00.00 Технологии материалов
- специальности 22.02.06 Сварочное производство
- ЕН.01 Математика.
1.2. Общее количество тестовых заданий
Количество заданий в комплекте оценочных материалов
|
Код компетенции |
Наименование компетенции |
Количество заданий |
|
|
Общие компетенции |
|||
|
ОК 01 |
Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес |
20 |
|
|
ОК 02 |
Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. |
28 |
|
|
ОК 03 |
Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность |
32 |
|
1.3 . Распределение тестовых заданий по компетенциям и дисциплинам
|
Код компетенции |
Наименование компетенции |
Наименование индикаторов сформированности компетенции |
Наименование дисциплины /модуля /практики |
семестр |
Номер задания |
|
ОК 01 |
Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес
|
Умения: У 01.01 распознавать
задачу и/или проблему У 01.02 владеть
актуальными методами работы Знания: З 01.01 актуальный
профессиональный З 01.02 алгоритмы
выполнения работ в профессиональной |
ЕН.01 Математика |
1, 2 |
1, 8, 9, 11, 13 |
|
ОК 02 |
Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество |
Умения: У 02.02 применять современную научную профессиональную терминологию; Знания: З 02.02 современная научная и профессиональная терминология |
ЕН.01 Математика |
1, 2 |
2, 4, 6, 10, 16, 18, 19 |
|
ОК 03 |
Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность |
Умения: У 03.01 анализировать задачу и/или проблему и выделять её составные части; У 03.02 определять этапы решения задачи. Знания: З 03.01 основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте; З 03.02 структуру плана для решения задач |
ЕН.01 Математика |
1, 2 |
3, 5, 7, 12, 14, 15, 17, 20 |
1.4. Распределение заданий по типу и уровням сложности
Вариант 1-4.
|
Код компетенции |
Индикатор сформированности компетенции |
Номер задания |
Тип задания |
Уровень сложности задания* |
Время выполнения |
|
ОК1 |
У 01.01, У 01.02 З 01.01, З 01.02 |
2 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК1 |
У 01.01, У 01.02 З 01.01, З 01.02 |
4 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
П |
3 – 5 мин |
|
ОК1 |
У 01.01, У 01.02 З 01.01, З 01.02 |
6 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК1 |
У 01.01, У 01.02 З 01.01, З 01.02 |
10 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК1 |
У 01.01, У 01.02 З 01.01, З 01.02 |
16 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК1 |
У 01.01, У 01.02 З 01.01, З 01.02 |
18 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
П |
3 – 5 мин |
|
ОК1 |
У 01.01, У 01.02 З 01.01, З 01.02 |
19 |
Задание открытого типа с развернутым ответом |
В |
5 – 10 мин |
|
ОК 2 |
У 02.02, З 02.02 |
1 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК 2 |
У 02.02, З 02.02 |
8 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
П |
3 – 5 мин |
|
ОК 2 |
У 02.02, З 02.02 |
9 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК 2 |
У 02.02, З 02.02 |
11 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
П |
3 – 5 мин |
|
ОК 2 |
У 02.02, З 02.02 |
13 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
П |
3 – 5 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
3 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
П |
3 – 5 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
5 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
7 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
12 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
14 |
Задание открытого типа с развернутым ответом |
П |
3 – 5 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
15 |
Задание открытого типа с развернутым ответом |
В |
5 – 10 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
17 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Б |
1 – 3 мин |
|
ОК 3 |
У 03.01, У 03.02 З 03.01, З 03.02 |
20 |
Задание открытого типа с развернутым ответом |
В |
5 – 10 мин |
1.5. Система оценивания выполнения тестовых заданий
|
Номер задания |
Указания по оцениванию |
Результат оценивания (баллы, полученные за выполнение задания / характеристика |
|
1 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
2 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
3 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
4 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
5 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
6 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
7 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
8 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
9 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
10 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
11 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
12 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
13 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
14 |
Задание открытого типа с развернутым ответом считается верным, если ответ совпадает с эталонным по содержанию и полноте |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
15 |
Задание открытого типа с развернутым ответом считается верным, если ответ совпадает с эталонным по содержанию и полноте |
Полный правильный ответ на задание оценивается 3 баллами; если допущена одна ошибка / неточность / ответ правильный, но не полный — 1 балл, если допущено более одной ошибки / ответ неправильный / ответ отсутствует — 0 баллов |
|
16 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
17 |
Задание комбинированного типа с выбором одного верного ответа из предложенных с обоснованием выбора ответа считается верным, если правильно указана цифра и приведены корректные аргументы, используемые при выборе ответа |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
18 |
Задание закрытого типа на установление соответствия считается верным, если правильно установлены все соответствия (позиции из одного столбца верно сопоставлены с позициями другого) |
Полное совпадение с верным ответом оценивается 1 баллом; неверный ответ или его отсутствие — 0 баллов |
|
19 |
Задание открытого типа с развернутым ответом считается верным, если ответ совпадает с эталонным по содержанию и полноте |
Полный правильный ответ на задание оценивается 3 баллами; если допущена одна ошибка / неточность / ответ правильный, но не полный — 1 балл, если допущено более одной ошибки / ответ неправильный / ответ отсутствует — 0 баллов |
|
20 |
Задание открытого типа с развернутым ответом считается верным, если ответ совпадает с эталонным по содержанию и полноте |
Полный правильный ответ на задание оценивается 3 баллами; если допущена одна ошибка / неточность / ответ правильный, но не полный — 1 балл, если допущено более одной ошибки / ответ неправильный / ответ отсутствует — 0 баллов |
Оценка «5» (отлично) соответствует результатам, содержащим от 19 до 24 правильных ответов из 20 вопросов теста.
Оценка «4» (хорошо) — от 15 до 18 правильных ответов.
Оценка «3» (удовлетворительно) — от 10 до 14 правильных ответов.
Оценка «2» (неудовлетворительно) — от 0 до 9 правильных ответов.
1.6. Описание дополнительных материалов и оборудования, необходимых для выполнения тестовых заданий
Дополнительные материалы и оборудование не требуются.
1.7. Продолжительность выполнения
Общее время, отведенное на выполнение заданий - 90 минут.
1.8. Инструкция по организации и проведению тестирования
Действия преподавателя во время проведения тестирования:
1) приветствует обучающихся;
2) объясняет обучающимся цель предстоящей работы: получение объективной информации о состоянии качества подготовки и освоения обучающимися основной профессиональной образовательной программы; доводит правила проведения тестирования;
3) устанавливает соответствие представленного профессиональной образовательной организацией списка группы и списка обучающихся, фактически присутствующих;
4) раздает обучающимся бланки заданий и бланки ответов;
5) знакомит со структурой заданий, отмечает особенности, объясняет правила заполнения бланков ответов;
6) обращается к обучающимся: «Есть ли вопросы?» (не имеет права отвечать на вопросы по содержанию заданий);
7) фиксирует время начала и время окончания работы на видном месте (доске);
8) отслеживает полную самостоятельность обучающихся при выполнении работы;
9) предупреждает обучающихся о том, что до конца процедуры осталось 10 мин;
10) по истечении времени выполнения работы собирает материалы работы (заполненные бланки ответов); проверяет соответствие количества работ числу испытуемых обучающихся;
11) благодарит обучающихся за участие в работе, желает успехов.
После завершения задания преподавателям выдаются эталоны ответов для каждого варианта заданий, работы проверяются преподавателями, проводящими проверочную работу согласно системе оценивания заданий и работы в целом. По итогу заполняется протокол
Действия обучающихся при выполнении тестового задания:
1) внимательно читайте все задания работы и указания по его выполнению;
2) если не можете выполнить очередное задание, не тратьте время, переходите к следующему;
3) только выполнив все задания, вернитесь к тем, которые у вас не получились сразу;
4) старайтесь работать быстро и аккуратно;
5) все задания выполнять на выданных листах;
6) если ошибся, зачеркни ошибку и выбери другой ответ;
7) после выполнения всех заданий осуществить проверку.
8) сдать заполненные бланки ответов преподавателю.
Сценарии выполнения тестовых заданий:
|
Тип задания |
Последовательность действий при выполнении задания |
|
Задание закрытого типа на установление соответствия |
1. Внимательно прочитать текст задания и понять, что в качестве ответа ожидаются пары элементов. 2. Внимательно прочитать оба списка: список 1 вопросы, утверждения, факты, понятия и т.д.; список 2 утверждения, свойства объектов и т.д. 3. Сопоставить элементы списка 1 с элементами списка 2, сформировать пары элементов. 4. Записать попарно буквы и цифры (в зависимости от задания) вариантов ответа |
|
Задание комбинированного типа с выбором верного ответа и обоснованием выбора из предложенных |
1. Внимательно прочитать текст задания и понять, что в качестве ответа ожидается только один из предложенных вариантов. 2. Внимательно прочитать предложенные варианты ответа. 3. Выбрать верный ответ, наиболее верный. 4. Записать только номер выбранного варианта ответа. 5. Записать аргументы, обосновывающие выбор ответа. |
|
Задание открытого типа с развернутым ответом |
1. Внимательно прочитать текст задания и понять суть вопроса. 2.Продумать логику и полноту ответа. 3.Записать ответ, используя четкие компактные формулировки. 4.В случае расчетной задачи, записать решение и ответ. |
2. Тестовые задания
Вариант 1.
Задание 1.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Матрица, называется ______________, если у нее количество строк равно количеству столбцов.
А); Квадратной; Б) Треугольной; В); Нулевой; Г) Обратной .
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 2.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Определитель
матрицы ![]() равен:
равен:
А) 5; Б) - 5; В) 8; Г) 0.
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 3.
Прочитайте текст и установите соответствие между записью алгебраических дополнений и элементами матрицы, к которым они относятся.
Дана матрица А = ![]()
|
А |
А12 |
1. |
|
|
Б |
А21 |
2. |
|
|
В |
А33 |
3. |
|
|
|
|
4. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 4.
Установите соответствие между следующими матрицами и необходимыми для их получения действиями:
Заданы
матрицы 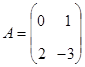 и
и 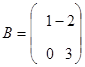
![]()
|
А |
|
1. |
А – 2В |
|
Б |
|
2. |
- А + В |
|
В |
|
3. |
- А – 2В |
|
|
|
4. |
А + 2В |
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 5.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Решить систему
уравнений по формулам Крамера: ![]() .
.
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 6.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции ![]() равно:
равно:
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 7.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции ![]() равно:
равно:
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 8.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из математических объектов является пределом функции на бесконечности? |
1. |
|
|
Б |
Какое выражение является неопределенностью вида «бесконечность на бесконечность»? |
2. |
|
|
В |
Какой из пределов является вторым замечательным? |
3. |
|
|
Г |
Какой из пределов является первым замечательным?
|
4. |
|
|
|
|
5. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 9.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Операция вычисления производной от функции называется:
А) потенцированием
Б) дифференцированием
В) логарифмированием
Г) интегрированием
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 10.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Производная функции sin (3х + 4) имеет вид:
А) cos (3x + 4) Б) – 3 cos (3x + 4) В) 3cos (3x + 4) Г) 7 cos (3x + 4)
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 11.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из математических объектов является производной второго порядка? |
1. |
|
|
Б |
Какой из математических объектов является сложной функцией? |
2. |
|
|
В |
Какая формула позволяет найти угловой коэффициент касательной к кривой графика функции? |
3. |
|
|
Г |
Какая формула вычисляет производную произведения? |
4. |
|
|
|
|
5. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 12.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Множество всех первообразных функций f(x) = 3x2 – 2x + 4 имеет вид
А) 6х – 2 Б) х3 – х2 + 4 + С
В) ![]() Г) х3
– х2 + 4х + С
Г) х3
– х2 + 4х + С
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 13.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какая из формул является формулой Ньютона – Лейбница? |
1. |
|
|
Б |
Какой из математических объектов является определенным интегралом? |
2. |
|
|
В |
Какой из математических объектов является криволинейной трапецией? |
3. |
|
|
Г |
Какой из математических объектов является определенным интегралом? |
4. |
|
|
|
|
5. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 14.
Вычислить
определенный интеграл:
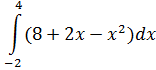
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 15.
Вычислите площадь фигуры, ограниченной линиями y= x, y = 5 – x, x = 1, x = 2.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 16.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Разделение переменных в дифференциальном уравнении ![]() приводит его к виду:
приводит его к виду:
А) 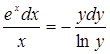 Б)
Б) 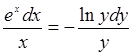
В) 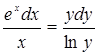 Г)
Г) 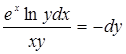
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 17.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Общее решение дифференциального уравнения у// + 4у = 0 имеет вид:
А) ![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 18.
Прочитайте текст и установите соответствие между начальными условиями и решениями уравнения у/ - х = 0, полученными при данных начальных условиях
|
А |
у (0) = 0 |
1. |
у = |
|
Б |
у (0) = 1 |
2. |
у = |
|
В |
у (2) = 0 |
3. |
у = |
|
|
|
4. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 19.
Набирая номер телефона, абонент забыл последние 3 цифры и набрал их наудачу, помня, что они различны. Найти вероятность того, что набраны нужные цифры.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 20.
В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 500 и десять выигрышей по 10 рублей. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Ответ: ___________________________________________________________________
Вариант 2.
Задание 1.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Матрица, называется ______________, если у нее элементы на главной диагонали равны 1, а остальные - 0.
А); Квадратной; Б) Единичной; В); Нулевой; Г) Обратной .
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 2.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Определитель
матрицы ![]() равен:
равен:
А) 11; Б) -7; В) -11; Г) 9.
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 3.
Прочитайте текст и установите соответствие между записью алгебраических дополнений и элементами матрицы, которым они относятся.
Дана матрица А = ![]()
|
А |
А13 |
1. |
|
|
Б |
А11 |
2. |
|
|
В |
А31 |
3. |
|
|
|
|
4. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 4.
Установите соответствие между следующими матрицами и необходимыми для их получения действиями:
Заданы
матрицы 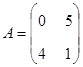 и
и 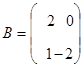
![]()
|
А |
|
1. |
А – 2В |
|
Б |
|
2. |
- А + В |
|
В |
|
3. |
- А – 2В |
|
|
|
4. |
А + 2В |
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 5.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Решить систему
уравнений по формулам Крамера: ![]() .
.
А) (3; 1); Б) (-2; 2); В) (4; -1); Г) (8; 0).
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 6.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции![]() равно
равно
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 7.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции 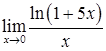 равно
равно
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 8.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из пределов является вторым замечательным? |
1. |
|
|
Б |
Какой из пределов является первым замечательным? |
2. |
|
|
В |
Какое выражение является неопределенностью вида «бесконечность на бесконечность»? |
3. |
|
|
Г |
Какое выражение является неопределенностью вида «ноль на ноль»? |
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 9.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Если
![]() на промежутке, то
функция:
на промежутке, то
функция:
А) постоянна на этом промежутке
Б) убывает на этом промежутке
В) возрастает на этом промежутке
Г) выпукла на этом промежутке
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
Задание 10.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Производная функции sin (5 + 2х) имеет вид:
А) cos (3x + 4) Б) – 2 cos (5 + 2x) В) 7 cos (5 + 2x) Г) 2cos (5 + 2x)
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 11.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какая формула вычисляет производную дроби? |
1. |
|
|
Б |
Какая формула вычисляет производную произведения? |
2. |
|
|
В |
Какая формула позволяет найти угловой коэффициент касательной к кривой графика функции? |
3. |
|
|
Г |
Какая из формул позволяет найти скорость по известному пути? |
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 12.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Множество всех первообразных функций f(x) = 2x – 4x3 + 2 имеет вид
А) х2 – х4 + С Б) 2 – 12 х2
В) х2 – х4 + 2х + С Г) х2 – х4 + 2 + С
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 13.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из математических объектов является определенным интегралом? |
1. |
|
|
Б |
Какой из математических объектов является неопределенным интегралом? |
2. |
|
|
В |
Какой из математических объектов является криволинейной трапецией?
|
3. |
|
|
Г |
Какая из формул является формулой Ньютона – Лейбница? |
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 14.
Вычислить
определенный интеграл:
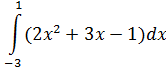
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 15.
Найти площадь фигуры, ограниченной линиями у=4-х2, у=3х, у=0 и находящейся в 1-й четверти.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 16.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Разделение переменных в дифференциальном уравнении ![]() приводит его к виду:
приводит его к виду:
А) ![]() Б)
Б) 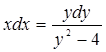
В) 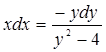 Г)
Г) ![]()
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 17.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Общее решение дифференциального уравнения у// - 4у = 0 имеет вид:
А) ![]() Б)
Б) ![]()
В) ![]() Г)
Г) ![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 18.
Прочитайте текст и установите соответствие между начальными условиями и решениями уравнения у/ + х = 0, полученными при данных начальных условиях
|
А |
у (0) = 0 |
1. |
у = |
|
Б |
у (0) = 1 |
2. |
|
|
В |
у (2) = 0 |
3. |
|
|
|
|
4. |
у = |
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
.
Запишите соответствующую последовательность цифр слева направо:
|
|
|
|
|
|
|
Задание 19.
В ящике 15 деталей, среди которых 10 окрашены. Сборщик наудачу выбрал 3 детали. Найти вероятность того, что детали окрашены.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 20.
В денежной лотерее выпущено 200 билетов. Разыгрывается один выигрыш в 300 и десять выигрышей по 50 рублей. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Вариант 3.
Задание 1.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Матрица, называется ______________, если каждую строчку исходной матрицы записать в виде столбца в том же порядке.
А); Квадратной; Б) Транспонированной; В); Нулевой; Г) Обратной .
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 2.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Определитель
матрицы ![]() равен:
равен:
А) - 8; Б) -5; В) 3; Г) 9.
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 3.
Прочитайте текст и установите соответствие между записью алгебраических дополнений и элементами матрицы, которым они относятся.
Дана матрица А = ![]()
|
А |
А12 |
1. |
|
|
Б |
А21 |
2. |
|
|
В |
А33 |
3. |
|
|
|
|
4. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 4.
Установите соответствие между следующими матрицами и необходимыми для их получения действиями:
Заданы
матрицы 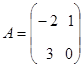 и
и 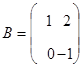
![]()
|
А |
|
1. |
А – 2В |
|
Б |
|
2. |
- А + В |
|
В |
|
3. |
- А – 2В |
|
|
|
4. |
А + 2В |
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 5.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Решить систему
уравнений по формулам Крамера: ![]() .
.
А) (2; -2); Б) (3; -1); В) (4; -1); Г) (8; 0).
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 6.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции ![]() равно
равно
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 7.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции 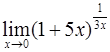 равно
равно
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 8.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из математических объектов является пределом функции на бесконечности? |
1. |
|
|
Б |
Какое выражение является неопределенностью вида «бесконечность на бесконечность»? |
2. |
|
|
В |
Какой из пределов является вторым замечательным? |
3. |
|
|
Г |
Какой из пределов является первым замечательным? |
4. |
|
|
|
|
5. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 9.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Точки максимума и минимума функции называются:
А) точками экстремума
Б) нулями функции
В) точками разрыва
Г) точками перегиба
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 10.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Производная функции cos (3х - 2) имеет вид
А) – 3 sin (3x - 2) Б) sin (3x - 2) В) 3sin (3x - 2) Г) – sin (3x - 2)
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 11.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какая формула вычисляет производную произведения? |
1. |
|
|
Б |
Какой из математических объектов является производной второго порядка? |
2. |
|
|
В |
Какая формула позволяет найти угловой коэффициент касательной к кривой графика функции? |
3. |
|
|
Г |
Какая из формул позволяет найти скорость по известному пути? |
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 12.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Множество всех первообразных функций f(x) = 3x2 + 2x –5 имеет вид
А) х3 + х2 + С Б) х3 + х2 – 5х + С
В) х3
+ х2 – 5 + С Г) ![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 13.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из математических объектов является неопределенным интегралом? |
1. |
|
|
Б |
Какая из формул является формулой Ньютона – Лейбница? |
2. |
|
|
В |
Какой из математических объектов является определенным интегралом? |
3. |
|
|
|
|
4. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 14.
Вычислить
определенный интеграл:
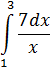
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 15.
Вычислить
площадь фигуры, ограниченной линиями![]() ,
,
![]() ,
, ![]() .
.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 16.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Разделение переменных в дифференциальном уравнении ![]() приводит его к виду:
приводит его к виду:
А) 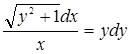 Б)
Б) 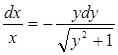
В) ![]() Г)
Г) 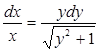
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 17.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Общее решение дифференциального уравнения у// + 9у = 0 имеет вид:
А) ![]() Б)
Б) ![]()
В)![]() Г)
Г) ![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 18.
Прочитайте текст и установите соответствие между начальными условиями и решениями уравнения у/ -2х = 0, полученными при данных начальных условиях
|
А |
у (0) = 0 |
1. |
у = х2 – 4 |
|
Б |
у (0) = 1 |
2. |
у = х2 + 1 |
|
В |
у (2) = 0 |
3. |
у = х2 |
|
|
|
4. |
у = х2 – 6 |
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 19.
В группе 12 студентов, среди которых 8 отличников. По списку отбирают 9. Найти вероятность того, что отберут 5 отличников.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 20.
В денежной лотерее выпущено 50 билетов. Разыгрывается один выигрыш в 1000 и десять выигрышей по 100 рублей. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Вариант 4.
Задание 1.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Матрица, называется ______________, если у нее количество строк равно количеству столбцов.
А) Обратной; Б) Треугольной; В); Нулевой; Г) Квадратной.
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 2.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Определитель
матрицы ![]() равен:
равен:
А) 4; Б) 0; В) -9; Г) 6.
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 3.
Прочитайте текст и установите соответствие между записью алгебраических дополнений и элементами матрицы, к которым они относятся.
Дана матрица А = ![]()
|
А |
А12 |
1. |
|
|
Б |
А21 |
2. |
|
|
В |
А33 |
3. |
|
|
|
|
4. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 4.
Установите соответствие между следующими матрицами и необходимыми для их получения действиями:
Заданы
матрицы 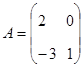 и
и ![]()
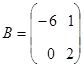
|
А |
|
1. |
А – 2В |
|
Б |
|
2. |
- А + В |
|
В |
|
3. |
- А – 2В |
|
|
|
4. |
А + 2В |
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 5.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Решить систему
уравнений по формулам Крамера: ![]() .
.
А) (3; 1); Б) (![]() ;
; ![]() ); В) (4; -1); Г) (
); В) (4; -1); Г) (![]() ;
; ![]() ).
).
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 6.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции 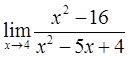 равно
равно
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 7.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Значение предела
функции ![]() равно:
равно:
![]()
![]()
![]()
![]()
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 8.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из пределов является первым замечательным? |
1. |
|
|
Б |
Какой из пределов является вторым замечательным? |
2. |
|
|
В |
Какой из математических объектов является пределом функции на бесконечности? |
3. |
|
|
|
|
4. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 9.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Действие, обратное нахождению производной, называется:
А) дифференцированием
Б) интегрированием
В) потенцированием
Г) логарифмированием
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 10.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Производная функции cos (5 + 4x) имеет вид
А) – sin (5 + 4 x) Б) – 4 sin (5 + 4x) В) sin (5 + 4x) Г) 4 sin (5 + 4x)
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 11.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какая формула вычисляет производную дроби? |
1. |
|
|
Б |
Какая формула позволяет найти угловой коэффициент касательной к кривой графика функции? |
2. |
|
|
В |
Какая из формул позволяет найти скорость по известному пути? |
3. |
|
|
Г |
Какая формула вычисляет производную произведения? |
4. |
|
|
|
|
5. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 12.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Множество всех первообразных функций f(x) = 4x3 + 2x -3 имеет вид
А) х4 + х2 – 3х + С Б) х4 + х2 + С
В) 12х2 + 2 Г) 4х4 + 2х2 – 3х + С
Ответ: _____________
Обоснование выбора ответа:________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 13.
Прочитайте текст и установите соответствие между формулой и математическим объектом:
|
А |
Какой из математических объектов является определенным интегралом? |
1. |
|
|
Б |
Какой из математических объектов является неопределенным интегралом? |
2. |
|
|
В |
Какой из математических объектов является криволинейной трапецией? |
3. |
|
|
Г |
Какая из формул является формулой Ньютона – Лейбница? |
4. |
|
|
|
|
5. |
|
|
|
|
6. |
|
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
Г |
|
|
|
|
|
Задание 14.
Вычислить
определенный интеграл:
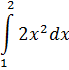
Решение: _________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 15.
Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2, х = 1.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 16.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Разделение переменных в дифференциальном уравнении ![]() приводит его к виду:
приводит его к виду:
А) 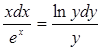 Б)
Б) ![]()
В) 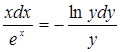 Г)
Г) ![]()
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 17.
Прочитайте текст, выберите правильный ответ и запишите аргументы, обосновывающие выбор ответа.
Общее решение дифференциального уравнения у// - 9у = 0 имеет вид:
А) ![]() Б)
Б) ![]()
В)![]() Г)
Г) ![]()
Ответ: _____________
Обоснование выбора ответа: ________________________________________________
_________________________________________________________________________
_________________________________________________________________________
Задание 18.
Прочитайте текст и установите соответствие между начальными условиями и решениями уравнения у/ +2х = 0, полученными при данных начальных условиях
|
А |
у (0) = 0 |
1. |
у = -х2 + 4 |
|
Б |
у (0) = 1 |
2. |
у = -х2 |
|
В |
у (2) = 0 |
3. |
у = -х2 + 1 |
|
|
|
4. |
у = х2 – 6 |
Запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ:
|
А |
Б |
В |
|
|
|
|
Задание 19.
Вычислить вероятность выпадения в сумме 10 очков при бросании пары костей.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
Задание 20.
В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 1000 и десять выигрышей по 10 рублей. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение: ________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
_________________________________________________________________________
__________________________________________________________________________________________________________________________________________________
Ответ: ___________________________________________________________________
2. Ключи к оцениванию тестовых заданий
|
№ задания |
Вариант 1 |
Вариант 2 |
Критерии |
||||||||||||||||
|
1 |
А Матрица, у которой число строк равно числу столбцов, называется квадратной |
Б Единичная матрица — это квадратная матрица, в которой все элементы главных диагоналей равны единице, а все остальные элементы — нулям |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
2 |
Б Решение:
|
В Решение:
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
3 |
А-3; Б-2; В-1
|
А-2; Б-1; В-3
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
4 |
А-3; Б-1; В-2
|
А-3; Б-2; В-1
|
1 б – полное правильное соответствие 0 б – остальные случаи
|
||||||||||||||||
|
5 |
Б Решение. Вычислим
определитель системы Система имеет единственное решение
Ответ:
|
А Решение. Вычислим
определитель системы Система имеет единственное решение
Ответ:
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
6 |
А
|
Б
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
7 |
Г
|
В
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
8 |
А-5; Б-1; В-2; Г-3 |
А-3; Б-6; В-5; Г-2 |
1 б – полное правильное соответствие 0 б – остальные случаи
|
||||||||||||||||
|
9 |
Г Процесс вычисления производной называется дифференцированием |
В Если производная функции y = f(x) положительна для любого x из интервала, то функция возрастает на этом интервале |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
10 |
В Решение: (sin (3х + 4)) / = cos (3x + 4) * (3х + 4) / = 3cos (3x + 4)
|
Г Решение: (sin (5 + 2х)) / = cos (5 + 2х) * (5 + 2х) / = 2cos (5 + 2х)
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
11 |
А-5; Б-1; В-4; Г-3 |
А-2; Б-5; В-1; Г-3 |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
12 |
Г Решение: F (х) = |
В Решение: F (х) = |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
13 |
А-2; Б-3; В-1; Г-3 |
А-4; Б-5; В-2; Г-6 |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
14 |
Решение:
|
Решение:
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
15 |
Решение: Воспользуемся формулой Ньютона-Лейбница:
|
Решение: Воспользуемся формулой Ньютона-Лейбница:
S=SOAB +SABC
|
3 б - полный правильный ответ 1 б – ответ правильный, но неполный / если допущена одна ошибка 0 б – ответ неправильный / ответ отсутствует |
||||||||||||||||
|
16 |
А Решение:
|
Б Решение: х(
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
17 |
Б Решение: Это однородное дифференциальное уравнение второго порядка. Для его решения необходимо сначала составить и решить характеристическое уравнение.
Таким образом, решение уравнения
|
А Решение: Это однородное дифференциальное уравнение второго порядка. Для его решения необходимо сначала составить и решить характеристическое уравнение:
Таким образом, решение уравнения
|
1 б – полное правильное соответствие 0 б – остальные случаи
|
||||||||||||||||
|
18 |
А-3, Б-1, В-2
|
А-3, Б-2, В-1
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
19 |
Решение. Событие А - номер набран верно
где m(А) = 1 - т.к. только один набор из 3-х цифр является нужным, а всего таких наборов
|
Решение. Событие А - 3 детали окрашены. Число благоприятствующих исходов:
Общее число возможных исходов:
|
3 б - полный правильный ответ 1 б – ответ правильный, но неполный / если допущена одна ошибка 0 б – ответ неправильный / ответ отсутствует |
||||||||||||||||
|
20 |
Решение: 1. Возможные значения выигрыша: х1 = 500, х2 = 10, х3 = 0. 2. Вероятности возможных значений: р1 = 1/100 = 0,01 (количество выигрышей в 500 рублей делится на общее количество билетов); р2 = 10/100 = 0,1 (количество выигрышей в 10 рублей делится на общее количество билетов); р3 = 1 – (0,01 + 0,1) = 0,89. Закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета:
|
Решение: 1. Возможные значения выигрыша: х1 = 300, х2 = 50, х3 = 0. 2. Вероятности возможных значений: р1 = 1/200 = 0,005 (количество выигрышей в 300 рублей делится на общее количество билетов); р2 = 10/200 = 0,05 (количество выигрышей в 50 рублей делится на общее количество билетов); р3 = 1 – (0,005 + 0,05) = 0,945. Закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета:
|
3 б - полный правильный ответ 1 б – ответ правильный, но неполный / если допущена одна ошибка 0 б – ответ неправильный / ответ отсутствует |
|
№ задания |
Вариант 3 |
Вариант 4 |
Критерии |
||||||||||||||||
|
1 |
Б Транспонированная матрица - матрица, полученная из исходной матрицы заменой строк на столбцы в том же порядке |
Г Матрица, у которой число строк равно числу столбцов, называется квадратной |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
2 |
В Решение:
|
В Решение:
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
3 |
А-3, Б-1, В-2
|
А-2, Б-3, В-1
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
4 |
А-2, Б-1, В-3
|
А-3, Б-2, В-1
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
5 |
Б Решение. Вычислим
определитель системы
Система имеет единственное решение
Ответ:
|
Г Решение. Вычислим определитель системы
Система имеет единственное решение
Ответ: |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
6 |
А
|
Г
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
7 |
В
|
Г
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
8 |
А-5; Б-3; В-4; Г-1 |
А-3; Б-4; В-1 |
1 б – полное правильное соответствие 0 б – остальные случаи
|
||||||||||||||||
|
9 |
А Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум - точка экстремума называется точкой минимума, а если максимум - точкой максимума |
Б Процесс вычисления производной называется дифференцированием. Обратный процесс - нахождение первообразной - интегрирование |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
10 |
А Решение: (соs (3х - 2)) / = - sin (3х - 2) * (3х - 2) / = - 3sin(3х - 2)
|
Б Решение: (соs (5 + 4x)) / = - sin (5 + 4x) * (5 + 4x) / = - 4sin(5 + 4x) |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
11 |
А-2; Б-6; В-4; Г-3 |
А-5; Б-2; В-1; Г-3 |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
12 |
Б Решение: F (х) = |
А Решение: F (х) = |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
13 |
А-2; Б-1; В-4 |
А-2; Б-3; В-5; Г-4 |
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
14 |
Решение:
|
Решение:
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
15 |
|
Решение:
|
3 б - полный правильный ответ 1 б – ответ правильный, но неполный / если допущена одна ошибка 0 б – ответ неправильный / ответ отсутствует |
||||||||||||||||
|
16 |
Г Решение:
|
А Решение: хydy=
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
17 |
Б Решение: Это однородное дифференциальное уравнение второго порядка. Для его решения необходимо сначала составить и решить характеристическое уравнение.
|
А Решение: Это однородное дифференциальное уравнение второго порядка. Для его решения необходимо сначала составить и решить характеристическое уравнение:
Таким образом, решение уравнения
|
1 б – полное правильное соответствие 0 б – остальные случаи
|
||||||||||||||||
|
18 |
А-3, Б-2, В-1
|
А-2, Б-3, В-1
|
1 б – полное правильное соответствие 0 б – остальные случаи |
||||||||||||||||
|
19 |
Решение.: Событие А - отобрали 5 отличников. Р (А) = где
n -
общее число способов выбора из 12 студентов 9 равно |
Решение: Рассмотрим все равновозможные исходы в результате бросания двух
костей (их число равно 36 - рекомендуем записать в
виде таблицы). Выпадение в сумме 10 очков
(событие А) возможно в трёх случаях – 4 очка
на первой кости и 6 на второй, 5 очков
на первой и 5 на второй, 6 очков
на первой и 4 на второй. Поэтому вероятность события
А (выпадения в сумме 10 очков) равна
|
3 б - полный правильный ответ 1 б – ответ правильный, но неполный / если допущена одна ошибка 0 б – ответ неправильный / ответ отсутствует |
||||||||||||||||
|
20 |
Решение: 1. Возможные значения выигрыша: х1 = 1000, х2 = 100, х3 = 0. 2. Вероятности возможных значений: р1 = 1/50 = 0,02 (количество выигрышей в 1000 рублей делится на общее количество билетов); р2 = 10/50 = 0,2 (количество выигрышей в 100 рублей делится на общее количество билетов); р3 = 1 – (0,02 + 0,2) = 0,78. Закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета:
|
Решение: 1. Возможные значения выигрыша: х1 = 1000, х2 = 10, х3 = 0. 2. Вероятности возможных значений: р1 = 1/100 = 0,01 (количество выигрышей в 1000 рублей делится на общее количество билетов); р2 = 10/100 = 0,1 (количество выигрышей в 10 рублей делится на общее количество билетов); р3 = 1 – (0,01 + 0,1) = 0,89. Закон распределения случайной величины Х – стоимости возможного выигрыша для владельца одного лотерейного билета:
|
3 б - полный правильный ответ 1 б – ответ правильный, но неполный / если допущена одна ошибка 0 б – ответ неправильный / ответ отсутствует |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.