Farg’ona Politexnika Inistituti

                   Qurilish fakulteti           Geodeziya Kartagrafiya va Kadastr                     yo’nalish

                  Geodeziya fanidan

‘’Yirik masshtabda planga olish uchun geodezik asos yaratishni loyihalash’’ mavzusida

KURS ISHI

Bajardi                                    15-18   guruh talabasi

                                               Umarxo’jayev Nasirilloxo’ja

Mavzu     Yirik mashtabda planga olish uchun geodezik asos yaratishni loyihalash

                                       REJA  

 Kirish

1.Trassani nivelirlash ,jurnalini hisoblash,profil chizish  

2.Garizantal burchak o’lchashning mohiyati

3. Yopiq polygon vedmistini hisoblash

4.Yirik mashtabdagi planga abris chizish

Hulosa

Foydalanilgan

                                       Kirish

Geodeziyaning  rivojlanish  tarixi.  Geodeziya  qadimiy  fanlardan  birdir. U  kishilik jamiyating  haYotiy  talablari  asosida  vujudga  kelgan  va  ishlab  chiqarish  kuchlarini taraqqiy  etishi  bilan  rivojlana  borgan.  Geodeziya  fani  Arabiston,  Xitoy,  Hindiston, O‘rta  Osiyoda  taraqqiy  etgan.  Masalan  IX  asrning  boshlarida  arab  xalifasi  Mamun

topshirig‘i  bilan  Mesopotomiya  tekisligida  er  sharining  kattaligini  aniqlash maqsadida Grado’s  o‘lchash  ishlari  olib borilgan. Olimlar er shari  meridianini 1 yoy uzunligini 111,8 km ekanligini aniqlaganlar.1680  yilda  I.  Nyuton  o‘zini  Do’nyo  tortilish  qonuniga  asoslanib,  er  -  ellipsoid shaklida degan  fikrni olg‘a surdi.  XIX  asr boshlarida  turli  mamlakatlarda  astronomiya,  geodeziya  sohasida  olib borilgan  ishlar  erni  shakli ellipsoiddan  bir  oz  farq  qilishini  ko‘rsatdi.  Masalan  ulug‘ olim  Laplas  Fransiya  va  boshqa  davlatlarda  olib  borilgan  Grado’s    o‘lchashlar natijasini  tahlil  qilib,  meridian  1   sining  uzunligi  ekvatordan  qutblarga  tomon  bir xilda  kamaymasligini  aniqladi.  shunga  asoslanib,  er  o‘ziga  xos  noaniq  shaklga  ega ekan,  degan  xulosaga  kelindi.  1873  yilda  nemis  fizigi  I.  V.  Listing  erning  bunday shaklini  geoid deb atalishini taklif etdi. Yerning  kattaligini  aniqlashda  Rossiyada  bajarilgan  Grado’s    o‘lchashning ahamiyati juda katta.

Masalan,  1816  yildan  boshlab  geodezist  K.I.Tenner  rahbarligida  Rossiyaning  harbiy  chegarasidagi  guberniyalarda,  astronom V.Ya.Struve  rahbarligida  Boltiq  bo‘yi guberniyalarida Grado’s  o‘lchash  ishlari olib borildi. Bu  ishlar  1850  yilgacha  davom  etgan  va  do’nay  daryosining  quyilish  joyidan  to Skandinaviya  yarim  orolining  shimoliy qirg‘og‘igacha  bo‘lgan  25  20    meridian yoyining  uzunligi  hisoblab chiqarilgan.“Muxandislik  geodeziyasi”  fanini  nazariy  jihatdan  rivojlantirishda  rus  olimlariP.L.CHebыshev,  A.P. Bolotov,  N.Ya.Singer,  A.A.Tillo  va  boshqalar  salmog‘li  hissa

qo‘shdilar.1928  yilda  mashhur  geodezist  F.N. Krasovskiy  davlat  territoriyasida  geodezik tayanch  shaxobchalarini  barpo  etish  va  topografik  plan  olish  ishlarining  dasturini tuzib chiqdi.1933  yilda  davlat  territoriyasini  gravimetrik  planini  olish  ishlari  olib  borildi. 1945  yilda  MDX  territoriyasini  1:1000000  masshtabli  kartalari  tuzildi.

Aerofototopografik  plan  olish  ishlariga  Drobishev,  Konshin,  Lobanov  va  boshqa olimlar  turli  injenerlik  inshootlarni  barpo  etishda  geodezik  ishlarini  bajarish uslublarini  yaratishga  olimlar  N.G.Vido’ev,  G.F.Glotov,  N.N.Lebedev  va  boshqalar katta hissa qo‘shdilar.Kartografiya  sohasida  ham  katta  yutuqlarga  erishildi  va  yirik  kartografik  asarlar yaratildi

1.Niverlirlash        Nivelirni  ishlatishdan  oldin  uning  quyidagi  geometrik  shartlarni qanoatlantirishi  tekshiriladi,  N-3  nivelirini  tekshirish  shartlari quyidagilardan iborat:

        Doiraviy  adilak  o`qi  nivelir  aylanish  o`qiga  parallel  bo`lishi  kerak, . Ko`targich vintlar orqali doiraviy adilak pufakchasi adilak qutisidagi  doira  markaziga  keltiriladi  va  nivelir  yuqori  qismi  180⁰buraladi.  Pufakcha  o`rtada  qolgan  bo`lsa,  shart  bajarilgan  bo`ladi,  aks holda  pufakcha  og`gan  qismining  yarmi  markazga  adilak  tuzatkich vintlari  bilan,  qolgan  yarmi  ko`targich  vintlar  bilan  markazga  keltiriladi.

Tekshirish nazorat uchun takrorlanadi. 

Bizda trassani niverlirlash topshirig’I berilgan unga kora 700 m masofada nevilirlash topshirig’i berilgan

Bizda olingan sanoqlar

Niverlirlash jurnali

Oldingi va orqadan olingan sanoqlarni ayirig yani qora va qizil sanoqlardan foydalangan holda ,oldindan olingan qora sanoqdan oldindan olingan qora sanoqni bir biridan ayirib nisbiy balandlikni olamiz va qizil sanoqdan ham hudi shunday amalni bajaramiz keyin esa ikkalasini ortacha qiymatini olamiz . Bizga malum bolgan Rp0 balandligiga shu chiqan nisbiy balandlikni qo’shamiz va hamma stansiyalarda shunday tartibda hisoblash amallarini bajaramiz.

H=a-b

Yani

a-oldingi reykadan olingan sanoq

b-orqa reykadan olingan sanoq

Rp1=424.66

Rp1+P0=424.66+0570=425.230

SHunday tartibda hisoblab balandlik otmetkalarini aniqlaymiz. Bizga keraklik otmetkalarni aniqlaganimizdan keyin , trassa pirofilini chizishga o’tamiz bunda esa belgilangan masshtab asosida chizamiz.

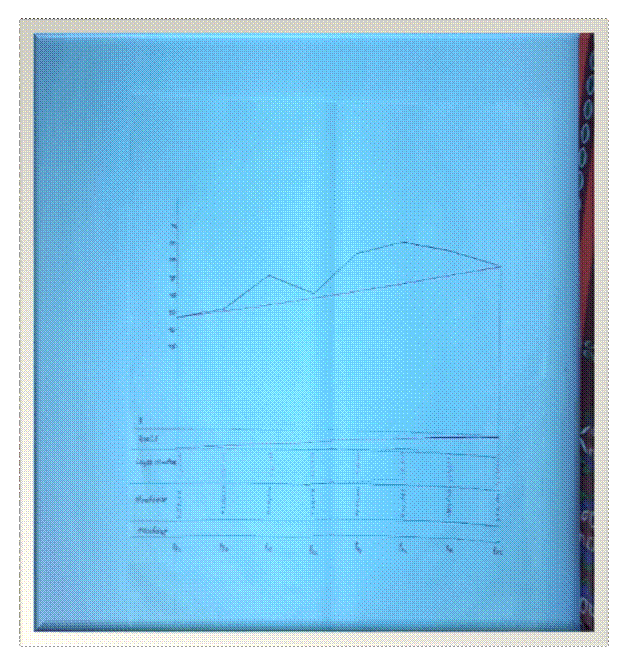
                       Garizantal masshtab 1;2000

                       Vertical masshtab 1;100

Bunda biz olchagan balandliklardan foydalanilgan holda loyiha otmetlasini hisoblaymiz, yani

Rp1-Rp2/St

Bunda Rp1,Rp2-nisbiy balandlik ,St-stansiyalar soni

Gorizontal burchak o’lchash mohiyati.

Joyda bir nuqtadan chiqqan ikki yoki bir necha yo‖nalish orasidagi burchaklarning  gorizontal  qo‖yilishini  o‖lchash  kerak  bo‖ladi.  Masalan,  V nuqtada    turib,  turli  balandlikda  yotuvchi  A  va  S  nuqtalarga qarash  yo‖li  bilan  ABC  burchakning  gorizontal  qo‖yilishi    ni  o‖lchash kerak  deylik.  Shakldan  ko‖rinadiki,  S  nuqta  balandda,  V  va  A  nuqtalar esa  S  ga  nisbatan  pastlikda.  Shunga  ko‖ra,  VA  va  VS  tomonlar  orasidagi  qiya tekislikdagi burchak desak ABCgorizontal proekstiyasi bo‖ladi. ning  qiymatini  aniqlash  uchun  shtativ  1  ustiga  aylanasi  graduslarga bo‖lingan  doira  2  gorizontal  vaziyatda  urnatiladi;  uning  markazi  O  dan chap  nuqta  S  ga  qarab  pch,  keyin  doirani  qo‖zg`atmay,  o‖ng  nuqta  A  ga qarab no‖ sanoqlar olinsa,  bu sanoqlar ayirmasiga teng bo‖ladi:=po‖-pch,  (1) ya‖ni  bir  nuqtadan  chiqqan  ikki  yo‖nalish  orasidagi  burchakning

gorizontal  qo‖yilishi  o‖ng  nuqtaga  qarab  olingan  sanoqdan  chap  nuqtaga qarab  olingan  sanoqning  ayirmasiga  teng.  Aylanasining  yo‖nalgan  qirrasi bo‖laklarga bo‖lingan va gorizontal holga keltirilib sanoq olinadigan doira 2  limb  deyiladi.  Agar  O  dan  S  ga  va  A  ga  qaralgan  ko‖rish  nurlaridan vertikal  tekisliklar  o‖tkazilsa,  bu  tekisliklar  kollimastion  tekisliklar deyiladi.Bu  tekisliklar  orasidagi  burchak  o‖lchanadigan  burchakning qiymati bo‖ladi.Ikki chiziq orasidagi burchakni goniometr yordamida ham o‖lchash mumkin.  Asosan,  burchakning  gorizontal  qo‖yilishi  teodolit  yordamida o‖lchanadi.

Bizda yopiq polygon vedmistini hisoblashimiz kerak bunga esa avalambor hisoblash ishini boshlashda o’lchangan burchak hisolaymiz.

B_n=[n-2]180⁰=7*180⁰=1260⁰ni tashkil qilishi kerak

Bizda olchangan qiymatlar

B_o’=[87⁰10.2’+216⁰17.5+95⁰39.5+180⁰27’+99⁰19.2’+216⁰23.5’+155⁰15.5+90⁰52’+118⁰38’]=1260⁰02.4’

F_b=B_o’-B_n bundan _foydalanib

F_b=1260⁰02.4’-1260⁰=0⁰02.4’

Bizda hatolik ruxsat etilgan darajada bo’lganligi uchun hisoblashni tuzatma kiritib davom etiramiz

Tuzatilgan burchaklardan foydalanib tomanlarnig direksion burchaklarini xisoblaymiz a_n=a_n-1+180⁰+B_n

Yani a₁ direksion burchak joyda olchangan shundan foydalanilgan holda qolgan burchaklarning direksion burchaklarini topamiz

A₂=104⁰21’+180⁰-87⁰10’=68⁰04’

A₃=68⁰04’+180⁰-216⁰17’=152⁰25’

Shunday tartibda qolgan tomonlarning direksion burchaklarini topamiz va oxirgi topilgan direksion burchakda ham huddi shunday ishni bajaramiz bunga sabab direksion burchakning to’g’ri hisoblanganligiga ishonch hosil qilamiz

A₁=11⁰31’+180⁰-87⁰10’=104⁰21’

Endi esa rumb burchakdan direksion burchakka o’tkazamiz

Rumb va direksion burchak orasidagi munosabat

Berilgan jadvaldan foydalanib direksion burchaklarni rumb burchakka o’tkazamiz

Rumb burchak qiymatlari va tomonlar garizantal quyilish qiymatlaridan foydalanib kordinata ortirmalari quyidagi formulalar yordamida hisoblanadi

   X_n=d_ncosr_n                                      X_n=d_nsinr_n

Kordinata ortirmalarining afsalyut bog’lanmasligi

F_abs[fx²+fy²]^-2

Koordinatalar otirmalarini hisoblash vedmisti [yopiq poligon]

Koordinatalar ortirmalarini xisoblash vedmisti [yopiq poligon]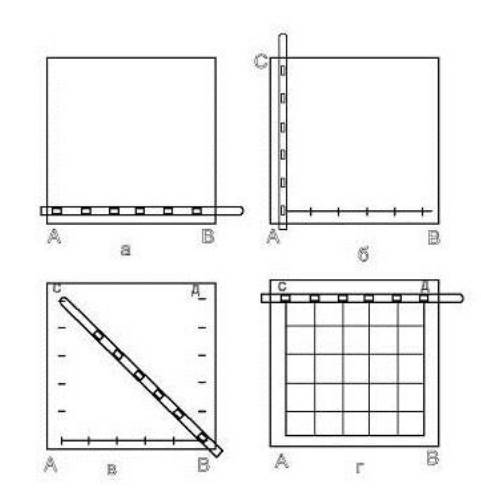

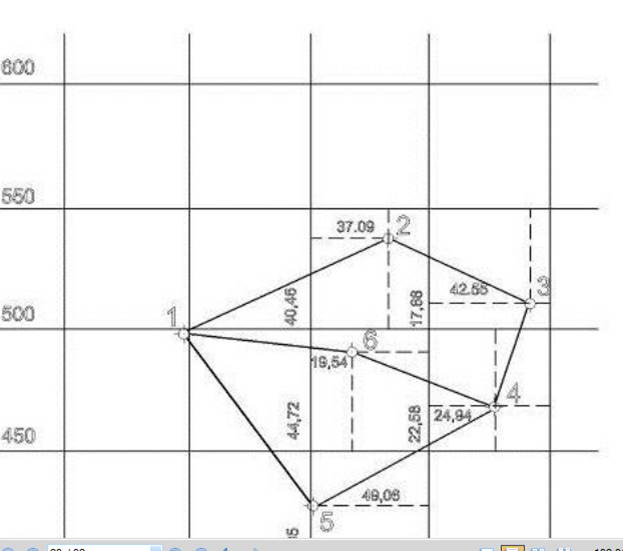
Kordinata ortirmalarini hisoblash uchun rumb burchak qiymatidan foydalanilgan holda

   X₁=104.15*cos [75⁰39’] =-25.83                                                            

   X_n=d_ncosr_n                                     

Shunday hisoblab kardinata ortirmalarini hisoblab topamiz delta x va delta y boyicha bizning hisob kitoblarimizga ko’ra delta X boyicha kordinata ortirmalari +- lar hisoblab chiqildi

-419.55

+419.78=0.18 bu kordinata ortirmasi pizning poligonda hisob kitob larimizga ko’ra ruhsat etiladigan qiymat bo’lgani uchun tuzatma kiritish yo’li bilan bu qiymatlarni tenglashtiramiz har bir topilgan ortirmaga -2 dan tarqatsak bu hatolikdan qutilgan bo’lamiz

Y boyicha ham hudi shunday hisoblash ishini bajarib tuzatma kiritamiz

Bizda topilgan kordinata ortirmalaridan foydalanib yani tuzatilgan kordinata ortirmalaridan foydalanib ,bizda birinchi nuqtaning kordinatasi malum shundan foydalanilgan holda quyidagi tartibda qolgan nuqtalarning kordinata ortirmalarini hisoblab chiqamiz

X₂=x₁+deltax₁

Yani

X_n=x_n-1+deltax_n-1

Y boyicha ham shunday xisob kitob qilamiz.  har bir nuqtaning kordinatalariga ega bolamiz.

Joyning  konturli  planini  chizish  uchun  avval,  joy  tafsiloti  s’yomka  qilinadi. Tafsilot  joyda  tabiiy  va  sun’iy  yo‘l  bilan  barpo  bo‘lgan  bino,  yo‘l,  ariq,  o‘rmon  elektr uzatish  liniyasi  va  boshqalardir,  ularning  o‘rni  va  shakli  to‘g‘ri  aniqlanishi  kerak. S’yomkada joyiga qarab quyidagi  usullar qo‘llaniladi.

Aylanma  usul.  Bunda  s’yomka  qilinadigan  joy  chegarasi  bo‘ylab  yopiq  polygon hosil  qilinadi.  Buning  tomon  va  burchak  uchlariga  asoslanib,  tafsilot  s’yomka

qilinadi.  Poligon  tomonlarining  uzunligi , ...., ,2 1 n d d d  tomonlar  orasidagi  o‘ng burchak  , ...., ,2 1 n    yoki  Chap  burchak  , ...., ,2 1 n    va  bir  yki  hamma  tomonlar

azimuti  ulchanadi  .  Tomonlarni  o‘lchashda  tomonning  ikki  yonida  20–40 m  gacha  bo‘lgan  tafsilot  harakterli nuqtalarining  o‘rni  shu  tomonga  nisbatan perpendikulyar  usuli  bilan  aniqlanadi.  O‘lchash  natijalari  abris  deyiladigan  varaqqa chiziladi  va  yoziladi.  chiziqni  to‘g‘ri  va  teskari  o‘lchash  natijalari  chiziq  oxirida  surat va  maxraj  holida  yoziladi  va  arifmetik o‘rtasi chiqariladida  yozib quyiladi.

Perpendikulyar  yoki  to‘g‘ri  burchakli  koordinatalarusuli.  Bu  usulda o‘lchanadiganchiziq  absissalar  o‘qi  deb,  uning  uchikoordinatalar  boshi,  absissalar o‘qiga  chiqarilgan  perpendikulyar  chiziqlar  esa  koordinatalar  o‘qi  deb  qabul  qilinadi. Tafsilot  harakterli  nuqtalarining  o‘rni  abssissa  (x) va  kordinata  (u) qiym atlari  buyicha aniqlanadi  .  Masalan,poligonning  AB  tomonini  o‘lchashda  uning  o‘ng

tomonidagi  binova  yo‘lni  s’yomka  qilish  ko‘rsatilgan.  AB  tomon  xo‘qi,  A  nuqta koordinatalar  boshi  deb  qabul  qilingan.  Binoning  chiziqdanko‘ringan  uchta burchagidan  xo‘qigaperpendikulyar  tushirilib,ularning  x  o‘qibilan  kesishgan nuqtalarining  o‘rni  koordinatalar  boshi  A  ga  nisbatananiqlangan,  16,00,  20,00  va 32,00  m  dagiperpendikulyarlar  uzunligi  o‘lchangan  va  bino  yoniga  yozilgan(20,01;va  14,0  m).  yo‘l  x  o‘qibilan  48,00   va  56,00  m  da kesishgan;  yo‘lyunalishini  aniqlash  uchun  60,00  m  da  x  ga perpendikulyar  chiqarilib,  uning  yo‘l  bilan  kesishgan  nuqtasining uzoqligi  4,00  mo‘lchangan.  Bu  ishdax  o‘qibuyicha  olingan masofalar  lenta  bilan,perpendikulyar  chiziqlar  uzunligi  esa ruletka  bilan  o‘lchanadi.  Chizik  va  unga  chiqarilgan perpendikulyar chiziqlar abris qog‘ozi.  joydagidek  chiziladi  va  o‘lchash  natijalari yoziladi.

Yopiq  poligon  tomonlarini  o‘lchashda  o‘ng  tomondagi,  ochiq  polygon tomonlarini (diagonal  yo‘lni) o‘lchashda esa ikki  tomondagi tafsilot s’yomka qilinadi. Perpendikulyar  chiziqlar  uzunligi  20  m  gacha  bo‘lganda  ular  chamalab, 40  m  gacha bo‘lganda  ekker  yordamida  chiqariladi.  S’yomka  qilingan  tafsilotni  planga tushirishda  ham  s’yomkadagidek  ishlanadi.  Poligon  tomonlari  chizilgach,  har  qaysi

tomonining  abrisi  buyicha  o‘lchangan  x  va  u  qiymatlari  masshtab  buyicha  qo‘yilib, nuqtalar topiladi: bu  nuqtalarni  abrisdagidek tutashtirilsa tafsilot  hosil bo‘ladi.

Abris  xomaki  plan  bo‘lib,  s’yomka  qilinadigan  joy    tafsiloti  va o‘lchash  natijalari  qo‘lda  mashtabsiz  chizilgan  chizmadir.  Burchak  o‘lchash  jurnalida maxsus  bet  bo‘lib,  unga  «abris»  deb  yozilgan  bo‘ladi;  abris  shu  betga  chiziladi.

O‘lchashda har qaysi tomon abrisi alohida  betga chiziladi.

Agar  tafsilot  murakkab  bo‘lmasa,  bir  betga ikki,  uch  tomon  abrisini  chizish  mumkin. S’yomkaning  hamma  usulida  ham  o‘ziga  xos  abris chiziladi Joy  plani  qog‘ozga  chizilganda  tafsilot  shu abrisga  ko‘ra  tasvirlanadi.  shuning  uchun  abrisda

joy  tafsiloti  to‘g‘ri  ko‘rsatilishi  va  aniq  o‘lchanishi kerak.                    

Kestirma  usuli.  Ma’lum  ikki  nuqta  orasidagi  masofa  va  uning  uchlarida o‘lchangan  burchak  tomonlari  yoki o‘lchangan  masofalarni  kesishtirish  orqali uchinchi  nuqta  o‘rnini  aniqlash  kestirma  usul  deyiladi.  Bu  usul,  ba’zan  ko‘shqutbiy (bipolyar)koordinatalar  usuli  deb  ham  yuritiladi.  Kestirma  ikki  usulga  bo‘linadi:

chiziqli kestirma va burchak kestirmasi chiziqli  kestirma  usuli.  Bu  usulda  s’yomka  qilinadigan  nuqta  o‘rni  shu  nuqtaga yaqin  bo‘lib,  o‘rni  asosiy  s’yomkada  aniqlangan  ikki  yoki  uch  nuqtadan  o‘lchangan masofa  buyicha  aniqlanadi.  Masalan,  asosiy  poligonning  BS  tomoniga  yaqin  yakka daraxt  yoki  ustun  o‘rnini  aniqlashda  B  va  S  nuqtadan  M  nuttagacha  bo‘lgan  masofa BM  va SM o‘lchanadi.

M  nuqtaning  plandagi  o‘rni  B  va  S  nuqtalardan  BM  va  CM  radiuslari  bilan chizilgan  yoylar kesishuvi orqali topiladi.

Burchak  kestirmasi.  Bu  usul  joyda  chiziq  uzunligini  o‘lchash  noqulay  bo‘lganda qo‘llaniladi.  Masalan,  CD  tomonga  nisbatan    daryoning  narigi  sohilini s’yomka  qilishda  Harakterli  uch  nuqta  (1,  2,  3)  belgilanadi.  Bu  nuktalar  o‘rnini aniqlash  uchun  poligon  tomoni  SD  bazis  deb  qabul  qilinadi  yoki  alohida  bazis o‘lchanadi.  Keyin  S  va  D  da  to‘rib  teodolit  bilan,   va ,3 D  da  to‘rib,   va ,3o‘lchanadi.  Bu  o‘lchash  natijalari  buyicha  1, 2, 3  nuqtalarining  plandagi  o‘rnini  ikki yo‘l  bilan  topish  mumkin.  AgarS  nuqtada  transportir  yordamida CD  ga  nisbatan2 1

,  va ,3  burchaklarni,  D  nuqtada  DC  ga  nisbatan

2 1,   va ,3  burchaklarini  yasab, burchak  tomonlarini davom  ettirsak  ular  kesishuvidan  1,2 va  3  nuqtalar  o‘rni  topiladi:

Burchak  yasashda  xato  katta  bo‘lganidan,  chiziqli  kestirma  usulidan  foydalanish

ma’qul  bo‘ladi.  Buning  uchun  sinuslar  teoremasi  buyicha

2 12 , 1   C a C va , 33a C hamda2 12 , 1 â D â D   va , 33â D   masofalar aniqlanadi

                            Hulosa

Ushbu kurs ishini  bajarish davomida geodeziyadan otilgan maruza , amaliy mashg’ulot va pitaktika darslaridsa otilgan mavzularni mustahkamlab olishimizga yordam beradi. Shu o’rinda yopiq polygon vedmistini xisoblash bizga geodeziyadan yaxshiroq bilim olishimizga yordam beradi. Yopiq polygon vedmistini xisoblash uchun har bir bosqicvhda aniq hisob kitob qilishimiz kerak chunki birgina etiborsiz qoldirilgan xato katta xatolarni keltirib chiqaradi. Yani odiygina burchaklardagi xato direksion burchaklarni to’g’ri chiqmasligiga olib keladi. Bizga berilgan topshiriqda yani 9 burchakli poligon ichki burchaklari yeg’indisi nazariy 1260⁰ ga teng bo’lishi kerak lelin teodalitda olingan sanoqlarda albatta hato boladi . yol qoyilgan hato ruxsat etarli bo’lsa hisoblash ishlari davom etiriladi aks holda sanoqlar boshqatdan olinadi. Amaliy olinga 9 burchakli poligon ichki burchaklari yeg’indisi 1260⁰02.4’ ni tashkil etdi bu esa yirik masshtabli poligonda ruxsat etarli bolganligi uchun biz olingan sanoqlarga tuzatma kiritamiz. Tuzatilgan qiymatlar boyicha hisoblash ishlarini davom etiramiz. bir  tomoning direksion burchagi malum bolsa  qolgan tomonlarning direksion burchaklarini hisoblab topamiz keyin esa direksion burchaklarni rumb burchakka otkazamiz. Tomonlarni quyilish masofasini rumb burchakni sin va cos qiyatlariga ko’paytirib delta X va delta Y larni topamiz va kordinata ortirmalari xatoligi ruxsat etilamaydigan darajada bolsa hisoblangan qiymatlarni boshidan boshqatdan tekshiriladi yani 0 dan boshqatdan o’lchanadi va xisoblanadi . ruxsat etarli darajada bolasa tuzatmalar kiritib hisoblash ishlari yakuniy bosqichga o’tkaziladi.

                        Foydalanilgan adabiyotlar

1 . Geodeziya-Qo’ziboyev.T. ‘’O’qtuvchi nashiryoti’’ Toshkent-1976

2.Geodeziya-O’tanov.O’, Nurmatov.E ‘’O’zbekiston’’Toshkent-2002

3.Injinerlik geodeziyasi-Norxojayev

4. Amaliy geodeziya

5 Injenerlik geodeziyasi uslubiy qollanmma –A.N.Inomov Toshkent2017

6.farpitalabalarigeodeziya telegram kanoli