Курсовая» Дидактические игры на уроках математики»

Оглавление

 

Введение

Глава 1. Теоретические основы развития познавательного интереса в процессе обучения математике

1.1. Психолого-педагогическое обоснование понятия «познавательный интерес»

1.2. Дидактическая игра и ее роль в развитии познавательного интереса

Глава 2. Практическое применение дидактических игр на уроках при изучении темы «Сложение и вычитание десятичных дробей» в 5 классе

2.1. Разработка конспектов уроков с использованием дидактических игр, их проведение и анализ

2.2. Опытно-экспериментальная работа. Анализ ее результатов

Заключение

Литература

Приложение

 

Введение

 

 Возникновение интереса к математике у значительного числа учащихся зависит в большей степени от методики ее преподавания, от того, насколько умело будет построена учебная работа. Надо позаботиться о том, чтобы на уроках каждый ученик работал активно и увлеченно, и использовать это как отправную точку для возникновения и развития любознательности, глубокого познавательного интереса. Это особенно важно в подростковом возрасте, когда еще формируются, а иногда и только определяются постоянные интересы и склонности к тому или иному предмету. Именно в этот период нужно стремиться раскрыть притягательные стороны математики.

Немаловажная роль здесь отводится дидактическим играм на уроках математики - современному и признанному методу обучения и воспитания, обладающему образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве. Современная дидактика, обращаясь к игровым формам обучения на уроках, справедливо усматривает в них возможности эффективной организации взаимодействия педагога и учащихся, продуктивной формы их общения с присущими им элементами соревнования, непосредственности, неподдельного интереса.

Игра - творчество, игра - труд. В процессе игры у детей вырабатывается привычка сосредоточиваться, мыслить самостоятельно, развивается внимание, стремление к знаниям. Увлекшись, дети не замечают, что учатся, познают, запоминают новое, ориентируются в необычных ситуациях, пополняют запас представлений, понятий, развивают фантазию. Дидактические игры очень хорошо уживаются с «серьезным» учением. Включение в урок дидактических игр и игровых моментов делает процесс обучения интересным и занимательным, создает у детей бодрое рабочее настроение, облегчает преодоление трудностей в усвоении учебного материала. Разнообразные игровые действия, при помощи которых решается та или иная умственная задача, поддерживают и усиливают интерес детей к учебному предмету. Игра должна рассматриваться как могущественный незаменимый рычаг умственного развития ребенка. Дидактическая игра - не самоцель на уроке, а средство обучения и воспитания. Игру не нужно путать с забавой, не следует рассматривать ее как деятельность, доставляющую удовольствие ради удовольствия. На дидактическую игру нужно смотреть как на вид преобразующей творческой деятельности в тесной связи с другими видами учебной работы.

В термине «дидактическая игра» подчеркивается ее педагогическая направленность, отражается многообразие применения. Актуальность темы в том, что математика  является важнейшей наукой и именно с ней человек встречается каждый день в своей жизни. Поэтому учителя серьезно относятся к обучению математике, делая уроки насыщенными. На то, чтобы уроки были интересными и занимательными, у учителей не хватает времени. В связи с этим ведутся поиски эффективных методов обучения, которые активизировали бы мысль школьников. Немаловажная роль здесь отводится дидактическим играм, которые  используется для развития познавательного интереса.

Цель:  подбор дидактических игр, развивающих познавательный интерес.

Задачи: - изучить и проанализировать психолого-педагогическую литературу в соответствии с темой работы;

- разработать конспекты уроков с использованием дидактических игр, их  провести и проанализировать;

-  провести анализ опытно-экспериментальной работы.  

Объектом исследования является игровая учебная деятельность на уроках математики.

Предмет исследования: процесс развития познавательного интереса учащихся 5 и 6 классов на уроках математики.

Гипотеза: использование дидактических игр на уроках математики влияет на развитие познавательного интереса у учащихся.

Игра – это феномен культуры. Она обучает, воспитывает, развивает, развлекает, дает отдых. Еще  А.С.Выготский подчеркивал, что «игра не должна исчезнуть из жизни ребенка, имея свое продолжение в дальнейшем школьном обучении и труде». Именно поэтому педагоги и психологи ориентируют на это воспитателей и учителей, подчеркивая, что создаваемые дидактические игры имеют функции интенсивного развития детей.

Дидактические игры, как уже отмечалось, в частности познавательные, дают возможность многогранного развития личности, развития способностей, сплочения детей на основе общих замыслов и интересов.

В своей работе я показывю всю важность дидактической игры в педагогическом процессе на примере использования игр на уроках математики в 5 и 6 классах. Прежде чем использовать игру на уроке, необходимо учитывать психологические особенности детей этого возраста и то, какие виды игр наиболее приемлемы для этого возраста.

Глава 1. Теоретические основы развития познавательного    интереса в процессе обучения математике

 

1.1.          Психолого-педагогическое обоснование понятия

«познавательный интерес»

 

Познавательный интерес – важнейшая область общего интереса. Его предметом является самое значительное  свойство человека: познавать окружающий мир не только с целью биологической и социальной ориентировки в действительности, но и  в самом  существенном отношении человека к миру – в стремлении проникать в его многообразие, отражать в сознании сущностные стороны, причинно-следственные связи, закономерности.

Интерес – сложное понятие, которое можно рассмотреть с позиций разных групп авторов. В переводе с  латинского языка слово «интерес» (interest) означает «имеет значение, важно ».

Филологи дают следующее определение: «Интерес – это особое внимание к чему-нибудь, желание вникнуть в суть, узнать, понять; занимательность, значительность».

С точки зрения психологов: «Интерес – это активная познавательная направленность человека на тот или иной предмет, явление или деятельность, связанная с положительным эмоциональным отношением к ней».

Значит, каковы бы ни были трактовки этого понятия, можно сказать, что значение интереса велико. Интерес побуждает к овладению знаниями, заставляют учеников активно работать, преодолевая трудности и препятствия.

Познавательный интерес – более узкое понятие, суть которого заключается в целенаправленном стремлении учащихся к овладению знаниями, в активном поиске новых способов углубления познания.

Познавательный интерес – важнейшее образование личности, которое складывается в процессе жизнедеятельности человека, формируется в социальных условиях его существования и никоим образом не является присущим человеку от рождения.

Познавательный интерес – интегральное образование личности. Интерес  имеет сложнейшую структуру, которую составляют как отдельные психические процессы: интеллектуальные, эмоциональные, регулятивные – так и объективные, и субъективные связи человека с миром, выраженные в отношениях.

 Познавательный интерес – явление многозначное, поэтому на процессы обучения и воспитания он может влиять различными своими сторонами. В педагогической практике познавательный интерес рассматривают часто лишь как внешний стимул этих процессов, как средство активизации познавательной деятельности учащихся, эффективный инструмент учителя, позволяющий ему сделать учебный процесс привлекательным, выделять в обучении именно те аспекты, которые могут привлечь к себе непроизвольное внимание учеников, заставить активизировать их мышление, волноваться и переживать, увлеченно работать над учебной задачей. «Смертный грех учителя – быть скучным» (Гербарт). Этот афоризм определяет понимание учителем места познавательного процесса в обучении, который рассматривается им как инструмент оживления учебного процесса.

Такой подход к познавательному процессу как внешнему стимулу обучения может иметь основания. Действительно, если из окружающего мира человек отбирает только то, что является для него более значимым, то следует задуматься над тем, что особо важное и значительное в обучении  нужно представить в интересной для учеников форме. Познавательный интерес на пути своего развития обычно характеризуется познавательной активностью, ясной избирательной направленностью учебных предметов, ценной мотивацией, в которой главное место занимают познавательные мотивы.

Познавательный интерес становится ценнейшим мотивом познавательной деятельности, если школьник проявляет готовность, стремление совершенствовать своё учение. Как мотив учения познавательный интерес имеет ряд преимуществ перед другими мотивами, которые могут существовать вместе и наряду с ним (коллективные, профессиональные, широкие социальные мотивы).

1.                 Познавательный интерес раньше других осознается школьником. «Интересно» – «неинтересно» – основные критерии его оценки. На вопрос «Что тебе нравится в школе?» значительная часть отвечают: «Интересно учиться, интересно каждый день узнавать новое».

2.                 Познавательный интерес в сравнении с другими мотивами более точно выражает мотивацию учения, ясно понимается.

3.                 Познавательный интерес более доступен для наблюдения. Его легче обнаружить, распознать, вызвать. А, следовательно, легче управлять его развитием.

4.                 Познавательный интерес является звеном в процессе мотивации и не обособлен от других мотивов, которыми одновременно руководствуется школьник. Он взаимосвязан с мотивами долга, ответственности, мотивами самоутверждения. Это необходимо учитывать, развивая познавательный интерес, потому что взаимосвязь мотивов обогащает личность, а интерес к познанию, обладая психологической основой, благотворно влияет на другие мотивы.

Проблема формирования познавательного интереса к математике представляет собой особую значимость для методики преподавания математики. Значительный вклад в разработку данной проблемы внесли Г.И.Щукина, Н.Г.Морозова, А.К.Маркова, А.Н.Леонтьев, В.Н.Мясищев.

По характеру проявления познавательного интереса в процессе изучения предмета выделяются уровни развития познавательного интереса: 1 – низкий уровень, 2 – средний и 3 – высокий уровень. [См. приложение 1]Так, у учащихся с низким уровнем развития познавательного интереса активность на уроках ситуативная, часты отвлечения, предпочтение отдается задачам репродуктивного характера, со стереотипными действиями. Учащиеся со средним уровнем развития познавательного интереса предпочитают также поисковый характер деятельности, но не всегда склонны к выполнению творческих заданий, их самостоятельная деятельность носит эпизодический характер, зависит от внешних стимулов. Учащиеся с высоким уровнем развития интереса отличаются  самостоятельностью, активным участием на уроке, предпочтением учебной деятельности более трудного характера.

Рассмотрим наиболее эффективный путь развития познавательно интереса к математике посредством задач. Выделим условия, которые необходимо соблюдать учителю при развитии интереса:

·                    владение понятием познавательный интерес(учителю необходимо знать, что такое «познавательный интерес», различать уровни развития данного интереса у учащихся);

·                    учет возрастных и индивидуальных особенностей;

·                    содержание задачи (задачи должны иметь интересное содержание, то есть формулировку и путь решения задачи);

·                    трудность задачи (следует учитывать, что при достаточно высокой трудности интерес к решению задачи снижается);

·                    свойство локальной устойчивости задачи (интерес к какой-либо задаче способен вызвать интерес к похожим задачам).

Сформулированные условия являются необходимыми: если соблюдать их, то возможно эффективное развитие познавательного интереса к математике. Сформулированные условия достаточны: развитие познавательного интереса к математике достигается соблюдением уже перечисленных условий.

Таким образом, развитие познавательных процессов школьников основывается на создании  интереса к предмету. Умелое применение учителем знаний по психологии, педагогике и по предмету в целом, дают гарантию результативности образовательного процесса.

Для  развития познавательного интереса на уроках математики используется   дидактическая игра. Остановимся на этом подробнее.

 

1.2.          Дидактическая игра и ее роль  в развитии познавательного

интереса учащихся

 

«Игровая деятельность – это особая сфера человеческой активности, в которой личность не преследует никаких других целей, кроме получения удовольствия от проявления физических и духовных сил» (О.С.Газман).[6,56]

Возникновение интереса к математике у значительного числа учащихся зависит в большей степени от методики ее преподавания, от того, насколько умело будет настроена учебная работа. Надо заботиться о том, чтобы на уроках каждый ученик работал активно, увлеченно, и использовать это как отправную точку возникновения и развития любознательности, глубокого познавательного интереса. Это особенно важно в подростковом возрасте, когда еще формируются, а иногда и только определяются постоянные интересы и склонности к тому или иному предмету. Именно в этот период нужно стремиться раскрыть притягательные стороны математики.

Немаловажная роль  отводится дидактическим играм на уроках математики.

Дидактическая игра - современный и признанный метод обучения и воспитания, обладающий образовательной, развивающей и воспитывающей функциями, которые действуют в органическом единстве.

Дидактические игры можно широко использовать как средство обучения, воспитания и развития. Основное обучающее воздействие принадлежит дидактическому материалу, игровым действиям, которые как бы автоматически ведут учебный процесс, направляя активность детей в определенное русло. Дидактическую игру следует отличать от игры вообще и игровой формы занятий, хотя это деление условное.

Природа создала детские игры для всесторонней подготовки к жизни. Поэтому они имеют генетическую связь со всеми видами деятельности человека и выступают как специфически детская форма и познания, и труда, и общения, и искусства, и спорта.

   Принято различать два основных типа игр: игры с фиксированными, открытыми правилами и игры со скрытыми правилами. Примером игр первого типа является большинство дидактических, познавательных и подвижных игр, сюда относят также развивающие интеллектуальные, музыкальные, игры-забавы, аттракционы.

Ко второму типу относят сюжетно-ролевые игры. Правила в них существуют неявно. Они – в нормах поведения воспроизводимых героев: доктор сам себе не ставит градусник, пассажир не летает в кабине летчика.

Дидактические игры различаются по обучающему содержанию, познавательной деятельности детей, игровым действиям и правилам, организации и взаимоотношениям детей, по роли преподавателя. Перечисленные признаки присущи всем играм, но в одних отчетливее выступают одни, в других – иные. В различных сборниках указано более 500 дидактических игр, но четкая классификация игр по видам отсутствует. Часто игры соотносятся с содержанием обучения и воспитания. В этой классификации можно представить следующие типы игр:

·                    Игры по сенсорному воспитанию

·                    Словесные игры

·                    Игры по ознакомлению с природой

·                    По формированию математических представлений и др.

Иногда игры соотносятся с материалом:

·              Игры с дидактическими игрушками,

·              Настольно-печатные игры,

·              Словесные игры,

·              Псевдосюжетные игры.

Такая группировка игр подчеркивает их направленность на обучение, познавательную деятельность детей, но не скрывает в достаточной мере основы дидактической игры – особенностей игровой деятельности детей, игровых задач, игровых действий и правил, организацию жизни детей, руководство учителя.

Условно можно выделить несколько типов дидактических игр, сгруппированных по виду деятельности учащихся.

·              Игры-путешествия

·              Игры-поручения

·              Игры-предположения

·              Игры-загадки

·              Игры-беседы (игры-диалоги).

Игры-путешествия имеют сходство со сказкой, ее развитием, чудесами. Игра-путешествие отражает реальные факты или события, но обычное раскрывается через необычное, простое – через загадочное, трудное – через преодолимое, необходимое – через интересное. Все это происходит в игре, в игровых действиях, становится близким ребенку, радует его. Цель игры-путешествия – усилить впечатление, придать познавательному содержанию чуть-чуть сказочную необычность, обратить внимание детей на то, что находится рядом, но не замечается ими. Игры-путешествия обостряют внимание, наблюдательность, осмысление игровых задач, облегчают преодоление трудностей и достижение успеха. Игры-путешествия всегда несколько романтичны. Именно это вызывает интерес и активное участие в развитии сюжета игры, обогащение игровых действий, стремление овладеть правилами игры и получить результат: решить задачу, что-то узнать, чему-то научиться.

Роль педагога в игре сложна, требует знаний, готовности ответить на вопросы детей, играя с ними, вести процесс обучения незаметно.

Игра-путешествие – игра действия, мысли, чувств ребенка, форма удовлетворения его потребности в знании.

В названии игры, в формулировке игровой задачи должны быть «зовущие слова», вызывающие интерес детей, активную игровую деятельность. В игре-путешествии используются многие способы раскрытия познавательного содержания в сочетании с игровой деятельностью: постановка задач, пояснение способов ее решения, иногда разработка маршрутов путешествия, поэтапное решение задач, радость от ее решения, содержательный отдых. В состав игры-путешествия иногда входит песня, загадки, подарки.

Игры-путешествия иногда неправильно отождествляются с экскурсиями. Существенное различие их заключается в том, что экскурсия – форма обучения и разновидность занятий. Целью экскурсии чаще всего является ознакомление с чем-то, требующим непосредственного наблюдения, сравнения с уже известным. Иногда игру-путешествие отождествляют и с прогулкой. Но прогулка чаще всего имеет оздоровительные цели. Познавательное содержание может быть и на прогулке, но оно является не основным, а сопутствующим.

Игры-поручения имеют те же структурные элементы, что и игры-путешествия, но по содержанию они проще и по продолжительности короче. В основе их лежат действия с предметами, игрушками, словесные поручения. Игровая задача и игровые действия в них основаны на предположении, что-то сделать: «Помоги Буратино расставить знаки в примерах», «Проверь домашнее задание у Незнайки».

Игры-предположения «Что было бы…?» или «Что бы я сделал…», «Как я решил  и почему?», и др. Иногда началом такой игры может послужить картинка, задание, задача, проблема и т.п.

Дидактическое содержание игры заключается в том, что перед детьми ставится задача и создается ситуация, требующая осмысления последующего действия. Игровая задача заложена в самом названии «Что было бы…?» или «Что бы я сделал…?». Игровые действия определяются задачей и требуют от детей целесообразно предполагаемого действия в соответствии с поставленными условиями или созданными обстоятельствами. Дети высказывают предположения, констатирующие или обобщенно-доказательные. Эти игры требуют умения соотнести знания с обстоятельствами, установления причинных связей. В них содержится и соревновательный элемент: «Кто быстрее сообразит?».

Игры-загадки. Возникновение загадок уходит в далекое прошлое. Загадки создавались самим народом, входили в обряды, ритуалы, включались в праздники. Они использовались для проверки знаний, находчивости. В этом и заключается очевидная педагогическая направленность и популярность загадок как умного развлечения.

В настоящее время загадки, загадывание и отгадывание рассматриваются как вид обучающей игры.

Основным признаком загадки является замысловатое описание, которое нужно расшифровать (отгадать и доказать). Описание это лаконично и нередко оформляется в виде вопроса или заканчивается им. Главной особенностью загадок является логическая задача. Способы построения логических задач различны, но все они активизируют умственную деятельность ребенка. Детям нравятся игры-загадки. Необходимость сравнивать, припоминать, думать, догадываться – доставляет радость умственного труда. Разгадывание загадок развивает способность к анализу, обобщению, формирует умение рассуждать, делать выводы, умозаключения.

Игры-беседы (диалоги). В основе игры-беседы лежит общение педагога с детьми, детей с педагогом и детей друг с другом. Это общение имеет особый характер игрового обучения и игровой деятельности детей. В игре-беседе учитель часто идет не от себя, а от близкого детям персонажа и тем самым не только сохраняет игровое общение, но и усиливает радость его, желание повторить игру. Однако игра-беседа таит в себе опасность усиления приемов прямого обучения.

Воспитательно-обучающее значение заключено в содержании сюжета – темы игры, в возбуждении интереса к тем или иным аспектам объекта изучения, отраженного в игре. Познавательное содержание игры не лежит «на поверхности», его нужно найти, добыть – сделать открытие и в результате что-то узнать.

Ценность игры-беседы заключается в том, что она предъявляет требования к активизации эмоционально-мыслительных процессов: единства слова, действия, мысли и воображения детей. Игра-беседа воспитывает умение слушать и слышать вопросы учителя, вопросы и ответы детей, умение сосредоточивать внимание на содержании разговора, дополнять сказанное, высказывать суждение. Все это характеризует активный поиск решения поставленной игрой задачи. Немалое значение имеет умение участвовать в беседе, что характеризует уровень воспитанности.

Основным средством игры-беседы является слово, словесный образ, вступительный рассказ о чем-то. Результатом игры является удовольствие, полученное детьми.

Перечисленными типами игр не исчерпывается, конечно, весь спектр возможных игровых методик. Однако на практике наиболее часто используются указанные игры, либо в «чистом» виде, либо в сочетании с другими видами игр: подвижными, сюжетно-ролевыми и др.

В основе любой игровой методики, проводимой на занятиях, должны лежать следующие принципы:

·              Актуальность дидактического материала (актуальные формулировки математических задач, наглядные пособия и др.) собственно помогает детям воспринимать задания как игру, чувствовать заинтересованность в получении верного результата, стремиться к лучшему из возможных решений.

·              Коллективность позволяет сплотить детский коллектив в единую группу, в единый организм, способный решить задачи более высокого уровня, нежели доступные одному ребенку, и зачастую – более сложные.

·              Соревновательность создает у учащегося или группы учащихся стремление выполнить задание быстрее и качественнее конкурента, что позволяет сократить время на выполнение задания с одной стороны, и добиться реально приемлемого результата с другой. Классическим примером указанных выше принципов могут служить практически любые командные игры: «Что? Где? Когда?» (одна половина задает вопросы – другая отвечает на них).

На основе указанных  принципов можно сформулировать  рекомендации к проводимым на занятиях дидактическим играм:

·              Каждая игра должна содержать элемент новизны.

·              Нельзя навязывать детям игру, которая кажется полезной, игра – дело добровольное. Ребята должны иметь возможность отказаться от игры, если она им не нравится, и выбрать другую игру.

·              Игра – не урок. Игровой прием, включающий детей в новую тему, элемент соревнования, загадка, путешествие в сказку и многое другое,… - это не только методическое богатство учителя, но и общая, богатая впечатлениями работа детей на занятии.

·              Эмоциональное состояние учителя должно соответствовать той деятельности, в которой он участвует. В отличие от всех других методических средств игра требует особого состояния от того, кто ее проводит. Необходимо не только уметь проводить, но и играть вместе с детьми.

·              Игра – средство диагностики. Ребенок раскрывается в игре во всех своих лучших и не лучших качествах.

Ни в коем случае нельзя применять дисциплинарные меры к детям, нарушившим правила игры или игровую атмосферу. Это может быть лишь поводом для доброжелательного разговора, объяснения, а еще лучше, когда, собравшись вместе, дети анализируют, разбирают, кто, как проявил себя в игре, и как надо было бы избежать конфликта.

Игровая форма занятий создается на уроках при помощи игровых приемов и ситуаций, которые выступают  как средство побуждения, стимулирования учащихся к математической деятельности.

Реализация игровых приемов и ситуаций при урочной форме занятий происходит по следующим основным направлениям: дидактическая цель ставится перед учащимися в форме игровой задачи; учебная деятельность учащихся подчиняется правилам игры; учебный материал используется в качестве средства  игры; в учебную деятельность вводится элемент соревнования, который переводит дидактическую задачу в игровую; успешность выполнения  дидактического задания связывается с игровым результатом.

Наблюдения показывают, что игровые приемы, использующие программный материал, и особенности игр школьников средних классов вызывают у них активизацию умственной деятельности, способствуют возникновению внутренних мотивов учения.

Идея игры состоит в том, что учитель  формирует учебную проблему или создает проблемную ситуацию, а учащиеся стараются решить эту проблему. Они понимают, что для решения проблемы им недостаточно имеющихся знаний.

Во время дидактической игры важным моментом является дисциплина. По мнению многих учителей, урок математики считается идеальным с точки зрения дисциплины, если школьники сосредоточены, внимательные, в меру активны, занимаются только индивидуальной самостоятельной работой. Они могут высказывать  свое мнение или вносить предложения только при поднятии руки или разрешения учителя.

Учитель, как правило, пресекает попытки ребят с ходу исправить замеченные ошибки, общаться между собой, оказывать друг другу посильную помощь. Это и понятно: хаотичное общение, подсказки, списывание приносят огромный вред.

Если же общение учеников сделать целенаправленным, таким, чтобы они почувствовали пользу от такого общения в процессе познавательной деятельности, то можно получить положительные результаты, как в обучении, так и в формировании личности, поскольку в этом случае по-настоящему реализуется принцип воспитания в коллективе.

Взаимопомощь и взаимоконтроль одновременно и упрощают, и усложняют работу учителя. Упрощают потому, что учитель получает возможность в ряде случаев перенести некоторые свои функции на школьников. Например, он может поручить  ученику, проконсультировать отстающих товарищей. Не секрет, что иногда отстающий школьник чувствует себя с товарищем более раскованно и занимается более успешно, чем с учителем. Что же касается усложнения работы учителя, то оно связано с необходимостью гибкого руководства познавательной деятельностью во время дидактической игры, удачного подбора групп (команд) и их руководителей.

Рассмотрим, в чем специфика дидактической игры, ее существенный признак. Во-первых, дидактическая игра имеет свою устойчивую структуру, которая отличает ее от всякой другой деятельности.

Во-вторых, основными структурными компонентами дидактической игры являются: игровой замысел, правила, игровые действия, познавательное содержание или дидактические задачи, оборудование, результаты игры. В отличие от игр вообще дидактическая игра обладает существенным признаком – наличием четко поставленной цели обучения и соответствующего ей педагогического результата, которые могут быть обоснованы, выделены в явном виде и характеризуются учебно-познавательной направленностью.

Остановимся более подробно на структурных компонентах дидактической игры. Игровой замысел -  первый структурный компонент игры – выражен, как правило, в названии игры. Он заложен в той дидактической задаче, которую надо решить в учебном процессе. Игровой замысел часто выступает в виде вопроса, как бы проектирующего ход игры, или в виде загадки. В любом случае он придает игре познавательный характер, предъявляет к участникам игры определенные требования в отношении знаний. Каждая дидактическая игра имеет правила, которые  определяют порядок действий и поведение учащихся в процессе игры, способствуют созданию на уроке рабочей обстановки. Поэтому правила дидактических игр должны разрабатываться с учетом цели урока и индивидуальных возможностей учащихся. Этим создаются условия для проявления самостоятельности, настойчивости, мыслительной активности, для возможности проявления у каждого ученика чувства удовлетворенности, успеха.

Кроме того, правила игры воспитывают умение управлять своим поведением, подчиняться требованиям коллектива.

Существенной стороной дидактической игры являются игровые действия, которые регламентируются правилами игры, способствуют познавательной активности учащихся, дают им возможность проявить свои способности, применить имеющиеся знания, умения и навыки для достижения целей игры. Очень часто игровые действия предваряются устным решением задачи.

Учитель, как руководитель игры, направляет ее в нужное дидактическое русло, при необходимости активизирует ее  ход разнообразными приемами, поддерживает интерес к игре, подбадривает отстающих учеников.

Основой дидактической игры, которая пронизывает собой ее структурные элементы, является познавательное содержание. Познавательное содержание заключается в усвоении тех знаний и умений, которые применяются при решении учебной проблемы, поставленной игрой.

Оборудование дидактической игры в значительной мере включает в себя оборудование урока. Это наличие технических средств обучения кодопозитивов, диапозитивов, диафильмов, видеофильмов, использование мультимедиа средств. Сюда также относятся различные средства наглядности: таблицы, модели, а также дидактические раздаточные материалы, грамоты, благодарности, подарки.

Дидактическая игра имеет определенный результат, который является финалом игры, придает игре законченность. Он выступает, прежде всего, в форме решения поставленной учебной задачи и дает школьникам моральное и умственное удовлетворение. Для учителя результат игры всегда является показателем уровня достижений учащихся, или усвоения знаний, или в их применении.

Все структурные элементы дидактической игры взаимосвязаны между собой, отсутствие основных из них разрушают игру. Без игрового замысла и игровых действий, без организующих игру правил, дидактическая игра или невозможна, или теряет свою специфическую форму, превращается в выполнение указаний, упражнений. Поэтому при подготовке к уроку, содержащему дидактическую игру, необходимо составить краткую характеристику хода игры (сценарий), указать временные рамки игры, учесть уровень знаний и возрастные особенности учащихся, реализовать межпредметные связи.

Сочетание всех элементов игры и их взаимодействие повышают организованность игры, ее эффективность, приводят к желаемому результату. Ценность дидактических игр заключается в том, что в процессе игры дети в значительной мере самостоятельно приобретают новые знания, активно помогают друг другу в этом.

При использовании дидактических игр очень важно следить за сохранением интереса школьников к игре. При отсутствии интереса или угасании его ни в коем случае не следует принудительно навязывать игру детям, так как игра по обязанности теряет свое дидактическое, развивающее значение; в этом случае из игровой деятельности выпадает самое ценное – ее эмоциональное начало. При потере интереса к игре учителю следует своевременно принять действия, ведущие к изменению обстановки. Этому могут служить эмоциональная речь, приветливое отношение, поддержка отстающих. При наличии интереса дети занимаются с большой охотой, что благотворно влияет и на усвоение ими знаний. Очень важно проводить игру выразительно. Если учитель разговаривает с детьми сухо, равнодушно, монотонно, то дети относятся к занятиям безразлично, начинают отвлекаться. Поэтому бывает трудно поддерживать их интерес, сохранять желание слушать, смотреть, участвовать в игре. Нередко это и совсем не удается, и тогда дети не получают от игры никакой пользы, она вызывает у них только утомление. Возникает отрицательное отношение к занятиям.

Учитель сам должен в определенной степени включаться в игру, иначе руководство и влияние его будут недостаточно естественными. Умение  включаться в игру тоже один из показателей педагогического мастерства. Интересная игра, доставившая детям удовлетворение, оказывает положительное влияние и на проведение последующих игр. При проведении дидактических игр забавность и обучение надо сочетать так, чтобы они не мешали, а, наоборот помогали друг другу. Средства и способы, повышающие эмоциональное отношение детей к игре, следует рассматривать не как самоцель, а как путь, ведущий к выполнению дидактических задач.  

Математическая сторона содержания игры всегда должна отчетливо выдвигаться на первый план. Только тогда игра будет выполнять свою роль в математическом развитии детей и воспитании интереса их к математике.

Дидактические игры в 5-6 классах часто бывают связаны с определенными сюжетами. Сюжеты эти весьма просты, рассчитаны на детское воображение. Иногда сюжеты подсказываются названием игры: «Магические квадраты», «Индивидуальное лото», «Кто быстрее», «Числовая мельница» и др.

Во многих играх взят принцип соревнования между группами ребят. Соревнования усиливают эмоциональный характер игр. При этом следует иметь в виду, что лучше, когда соревнование проводится не на личное первенство, а на первенство команды учащихся, сидящих в одном ряду, чтобы дети не только сами стремились хорошо выполнить задание, но и побуждали к этому своих товарищей, помогали им. Мотив соревнования может быть выражен по-разному, в частности в названии игр: «Кто скорее», «Кто вернее», «Хоккей», «Телефон» и другие.

Целесообразность использования дидактических игр на разных этапах урока различна. Так, например, при усвоении новых знаний возможности дидактических игр значительно уступают более традиционным формам обучения, поэтому игровые формы занятий чаще применяют при проверке результатов обучения, выработке навыков, формировании умений. Определение места дидактической игры в структуре урока и сочетание элементов игры и учения во многом зависят от правильного понимания учителем функций дидактических игр и их классификации. В первую очередь коллективные игры в классе следует разделять по дидактическим задачам урока. Это, прежде всего игры обучающие, контролирующие, обобщающие. Обучающей будет игра, если учащиеся, участвуя в ней, приобретают новые знания, умения и навыки или вынуждены приобрести их в процессе подготовки к игре. Причем результат усвоения знаний будет тем лучше, чем четче  будет выражен мотив познавательной деятельности не только в игре, но и в самом содержании математического материала.

Контролирующей будет игра, дидактическая цель которой состоит в повторении, закреплении, проверке ранее полученных знаний. Для участия в ней каждому ученику необходима определенная математическая подготовка.

Обобщающие игры требуют интеграции знаний. Они способствуют установлению межпредметных связей, направлены на приобретение умения действовать в различных учебных ситуациях.

При организации дидактических игр необходимо придерживаться следующих положений:

1.            Правила игры должны быть простыми, точно сформулированными, а математическое содержание предлагаемого материала – доступно пониманию школьников. В противном случае игра не вызовет интереса и будет проводиться формально.

2.            Игра должна давать достаточно пищи для мыслительной деятельности, в противном случае она не будет содействовать выполнению педагогических целей, не будет развивать математическую зоркость и внимание.

3.            Дидактический материал, используемый во время игры, должен быть удобен в использовании.

4.            При проведении игры, связанной с соревнованиями команд, должен быть обеспечен контроль за ее результатами со стороны всего коллектива учеников или выбранных лиц. Учет результатов должен быть открытым, ясным и справедливым.

5.            Каждый ученик должен быть активным участником игры.

6.            Легкие и более трудные игры должны чередоваться, если на уроке проводится несколько игр.

7.            Игровой характер при проведении уроков по математике должен иметь определенную меру.

8.            В процессе игры учащиеся должны математически грамотно проводить свои рассуждения, речь их должна быть правильной, четкой, краткой

9.            Игру нужно закончить на данном уроке, получить результат. Только в этом случае она сыграет положительную роль

Дидактическая игра является средством умственного развития, так как в процессе игры активизируются разнообразные умственные процессы. Чтобы понять замысел, усвоить игровые действия и правила, нужно активно выслушать и осмыслить объяснение учителя. Решения задач, поставленных играми, требуют сосредоточенного внимания, активной мыслительной деятельности, выполнения сравнения и обобщения. Исходя из особенностей предмета математики, следует различать игры-состязания и игры-олимпиады. В первом случае победа обеспечивается в основном за счет скорости выполнения вычислений, преобразований, но без ущерба качеству выполнения задания, во втором – победа обеспечивается главным образом за счет качества решений задач повышенной трудности. Первые полезны для выработки автоматизма действий, вторые – для воспитания серьезного отношения к математике.

Таким образом, в игровых формах занятий реализуются идеи совместного сотрудничества, соревнования, самоуправления, воспитания через коллектив, приобщения детей к научно-техническому творчеству, воспитанию ответственности каждого за учебу и дисциплину в классе, а главное – обучения математике. Игра способствует формированию прочных вычислительных навыков и умений, также играет огромную роль в развитии познавательного интереса как одного из важнейших мотивов учебно-познавательной деятельности, развития логического мышления, и развития личностных качеств ребенка.

Глава 2. Практическое применение дидактических игр  на уроках математики при изучении темы «Сложение и вычитание десятичных дробей»

2.1. Разработка конспектов уроков с использованием

дидактических игр, их проведение и анализ

 

Изучив теорию данного вопроса, у автора возникло желание и интерес реализации этого на практике. Для того чтобы доказать или опровергнуть, что использование дидактических игр на уроках математики развивает интерес у учащихся, автором были разработаны и проведены 12 уроков с использованием дидактических игр. Уроки с использованием дидактических игр проводились только в экспериментальном 5а классе. В контрольном 5б классе проводились традиционные уроки.

По тематическому  планированию данная тема включает следующие вопросы:

·              Десятичная запись дробных чисел (2ч)

·              Сравнение десятичных дробей (2ч)

·              Сложение и вычитание десятичных дробей (5ч)

·              Приближенные значения чисел. Округление чисел (3ч).

Конспект урока по теме «Десятичная запись дробных чисел»

Цели урока: -  знакомство учащихся с десятичной записью дробных чисел,с правилами их записи и чтения;

-  развитие вычислительных навыков и математической речи учащихся;

-  воспитание интереса к математике.

Оборудование: карточки к «Математической эстафете», наглядность.

Ход урока

1.                 Сообщение темы и целей урока

2.                 Анализ контрольной работы по теме «Обыкновенные дроби»

3.                 Устные упражнения

 

Игра «Математическая эстафета»

Каждому ученику раздается карточка с одним звеном цепочки. Необходимо решить эту цепочку. Выиграет тот, кто сделает это быстро и правильно. После того как все учащиеся решат, три учащихся, которые решили правильно и быстро, награждаются грамотой победителей в «Математической эстафете».

4.                 Изучение нового материала

5.                 Закрепление изученного материала

5.1. №1118 (устно)

5.2. №1117 (по цепочке у доски)

5.3. №1120 (а,б-учителем у доски; в,г- самостоятельно)

6. Домашнее задание: п.30 №1139(а), №1140, №1141

7. Итог урока (вопросы после параграфа).

Самоанализ

 На уроке были  использованы метод объяснения материала учителем. Сообщены тема и цели урока. Время на уроке распределено. Устные упражнения проведены в форме игры «Математическая эстафета». В данной игре важным стимулом является элемент соревнования. Это задание заинтересовало всех детей без исключения. Во время игры дети активно решали примеры, чтобы быть первыми. Большинство учеников пришли к правильному ответу, но трое из них были самыми быстрыми и все правильно решили. Они были награждены грамотами победителей. Для остальных ребят это послужило стимулом к тому, чтобы в следующий раз быть первыми. Данная игра настроила  детей на работу. Учащиеся работали активно, поэтому  поставленные  цели реализованы. План был выполнен. Итог урока подведен.

Конспект урока по теме «Сложение и вычитание десятичных дробей»

Цели урока: - знакомство учащихся со сложением и вычитанием десятичных дробей;

   - развитие вычислительных навыков, математической речи;

   - воспитание интереса к предмету, аккуратности.

Оборудование: карточки для игры, изображение слона

Ход урока

1.                 Сообщение темы и целей урока

2.                 Устные упражнения (Игра «В мире животных»)

Самое крупное наземное животное – африканский слон. С помощью рисунка узнайте:

 

 

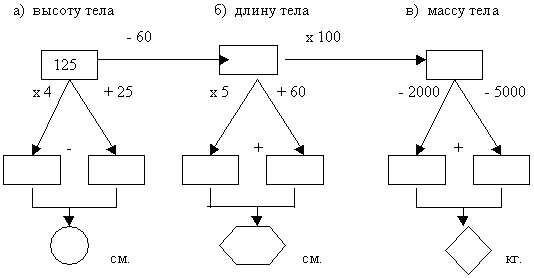
Выразите высоту и длину тела слона в метрах.

Высота тела: 350см = 3,5м. Длина тела: 450см = 4,5м. Масса тела: 6000кг = 6т.

3.                 Изучение нового материала

3.1. Объяснение учителем

3.2. Работа в группах

4. Закрепление изученного материала

4.1. № 1184 (у доски с полным объяснением)

4.2. №1186 (по цепочке у доски)

4.3. №1187 (4 человека у доски, остальные в тетрадях)

4.4. №1188 (самостоятельно)

5. Домашнее задание: №1228(а, б, в) №1229(а, б, в) №1230

6. Итог урока: вопросы после параграфа

Самоанализ

На уроке были  использованы метод объяснения нового материала учителем, групповая форма работы. Сообщены тема и цели урока. Время на уроке распределено. Устные упражнения проведены в форме игры «В мире животных». Это задание заинтересовало всех детей без исключения. Во время игры дети активно решали примеры, чтобы узнать какую высоту, длину и массу тела имеет африканский слон. Большинство учеников пришли к правильному ответу, но  некоторые не могли перевести  сантиметры в метры. Игра носит познавательный характер, так как во время игры дети получают дополнительные знания. Данная игра настроила  детей на работу. На уроке были использованы разные виды проверки, формы организации работы учащихся. Учащиеся работали активно, поэтому  поставленные  цели реализованы. План был выполнен. Итог урока подведен.

Конспект урока по теме «Сложение и вычитание десятичных дробей»

Цели урока: - закрепление знаний по сложению и вычитанию десятичных дробей, разложению десятичных дробей по разрядам, сравнению десятичных дробей;

- развитие вычислительных навыков, математической речи учащихся;

    - воспитание интереса к предмету.

Оборудование: карточки для устного счета, самостоятельной работы.

Ход урока

1. Сообщение темы и целей урока

2. Устные упражнения Игра «Умная лесенка»

 

На каждой ступеньке записано задание в одно действие. Класс делится на команды по 6 человек. Каждый ученик решает по очереди свой пример, и записывает ответ на своей «ступеньке». Шестой ученик ответы складывает. Результат записывает в треугольник.

 

0,7+8=                                                                                           ?

11,2+4=

7,3+6,7=                                                                      +

                                                                  +

0,3+5=

                                             +

1,5+2,3=           +

 

 

 

 

1.                 Работа по теме урока

1.1.                                  №1203 (устно)

1.2.                                  №1207 (у доски)

1.3.                                  №1211 (2 человека у доски, остальные в тетрадях)

1.4.                                  Задание на карточке

2.                 Домашнее задание №1236(в, г) №1240

3.                 Итог урока. Самостоятельная работа

Самоанализ

На уроке была  использована групповая форма работы. Сообщены тема и цели урока. Время на уроке распределено. Устные упражнения проведены в форме игры «Умная лесенка». Это задание заинтересовало всех детей без исключения. Во время игры дети активно решали примеры, чтобы как можно быстрее решить пример и передать эстафету другому ученику. Групповая форма помогла организовать детей. Во время игры развивала умение работать в группе.  Данная игра настроила  детей на работу. На уроке были использованы разные виды проверки, формы организации работы учащихся. Учащиеся работали активно, поэтому  поставленные  цели реализованы. План был выполнен. Итог урока подведен. Самостоятельная работа дала следующие результаты: «5»- 12, «4»- 8, «3»- 4, «2»-нет.

Конспект урока по теме «Приближенные значения чисел. Округление чисел»

Цели урока:  - развитие познавательного интереса учащихся

путем использования  дидактических игр на уроке;

- формирование умения выполнять арифметические действия   

с десятичными дробями;

- формирование умения работать в парах и микрогруппах;

- воспитание интереса к предмету.

Оборудование: карточки

 Ход урока

1.Устная работа.

   Сегодня мы с вами отправимся в путешествие. Путь наш лежит в средневековый город на рыцарский турнир.

Перед дальней дорогой необходимо подкрепиться. А так как мы отправимся в математический город на математический рыцарский турнир, то нам необходимо подкрепиться знаниями.

 Повторение теории по пунктам 30-32 учебника.

Вопросы: 1). Какие обыкновенные дроби можно записать в виде десятичных дробей?

2). Как определить количество цифр после запятой в десятичной записи

дроби?

3).Назовите первые 4 разряда после запятой в десятичных дробях.

4). Сформулируйте правило сложения (вычитания) десятичных дробей.

5). Сформулируйте  правило сравнения десятичных дробей.

Хорошо, молодцы!Ну, а теперь можно и в путь!

2.Игра:  «Рыцарский турнир».

1). Попасть в средневековый город непросто. Чтобы преодолеть временное пространство, необходимо пройти через математический лабиринт.

Время на прохождение лабиринта у вас ограничено; первые три человека, прошедшие лабиринт будут тремя рыцарями –участниками рыцарского турнира, все остальные – это их команда.

Учащимся предлагается задание «Математический лабиринт»

Математический лабиринт.

Вход в лабиринт: задание № 1

Выход из лабиринта:  ответ совпадает с номером задания.

№ 1.  Выполните действия:   8,65  -  5,7 + 1,05

№ 2. Решите уравнение:  ( х + 1,7 ) – 3,3 = 0,4

№ 3. Решите задачу:

Расстояние между городами 120 км. Из городов навстречу друг другу одновременно выехали два велосипедиста со скоростью 13,6 км/ч и 10,4 км/ч соответственно. Через сколько часов они встретятся?

№ 4. Найдите периметр треугольника АВС, если АВ = 0,4 м, ВС больше АВ на 0,65 м, но меньше АС на 0,5 м.

№ 5.  Вычислите:   ( 24,67 + 15,33 )  :  ( 88,9 – 68,9 )

( Примечание:   Ключ к лабиринту:  № 1    № 4  № 3№ 5 № 2  ).

2).  Рыцарский турнир:  «Кто быстрее?». Математическая эстафета.

Бланк с заданием получают ученики, сидящие за первой партой. Каждый решает одно задание и передает назад. Ученики, сидящие за последней партой, называют окончательный ответ.

1 вариант.

 

2,7

        + 2,8           + 4,9             + 2,4              : 2  

 

 

 2 вариант.

 

3,8

       + 1,8              12               + 1,3             - 5,3  

 

 

3).2.рыцарский турнир:  «Кто дальше?».

Рыцари – участники соревнования по стрельбе из лука. Сначала с помощью жеребьевки определяем  номер лука. Далее надо найти значение выражения, соответствующего данному номеру. Полученный ответ будет определять дальность полета стрелы каждого участника. Отметив положение стрелы на числовом луче, определите, кто победил!

Каждая парта получает бланк с соответствующим заданием. На доске (или с помощью кодоскопа) изображен числовой луч, на котором цветными магнитами первые выполнившие задание отмечают полученные числа.

Бланк с заданием:

II рыцарский турнир:«Кто дальше? ».

1). Методом жеребьевки определите номер своего лука со стрелой.

2). Найдите значение выражения соответствующего указанному номеру.

3). Полученный ответ определяет дальность полета стрелы каждого

участника.

4).Отметив положение стрелы на координатном луче, определите, кто победил.

 

№ 1.  ( 6.42 + 4,9 ) + ( 17,26 – 16,08 )

№ 2.  2 + ( 2,82 + 4,36 ) – ( 0,67 + 3,41 )

№ 3.  ( 25,9 -  6,2 ) – ( 19,374 + 4,626) : 3

№ 4.  ( 42,75 – 37,26 ) + ( 17,32 – 12,31 ) +

№ 5.  3 - ( 6,03 + 4,27 ) – ( 3,7 + 1,2 ) -

 

4). 3. рыцарский турнир:  «Самый зоркий».

Расшифруй слово. Что оно означает?

Учащиеся получают бланк с заданием, на котором зашифровано два слова (1 и 2 варианты).

Ответы:  Мицар  и Алькор  - звезды в созвездии Большой медведицы.

С помощью кодоскопа рассмотреть изображение Большой медведицы и расположение указанных звезд.

Бланк с заданием:

III рыцарский турнир:  «Самый зоркий!».

1 вариант.

Расшифруйте слово!  Что оно обозначает?

Ц 12,1 – ( х + 5.8 ) = 1,7

 

Р( у – 3,7 ) – 1,8 = 4,7

 

М ( 2,9 + х ) – 3,5 = 4,5

 

И14,08 – ( 52,3 – х ) = 1,003

 

А 6,793 х + 0,007 х + х = 7042

5,1

39,223

4,6

1006

10,2

 

 2 вариант.

Расшифруй слово! Что оно обозначает?

 

Р ( у – 3,7 ) – 1,8 = 4,7

 

Ь 13,2 - ( 5,7 + х ) = 3,9

 

О ( 39,4 – х ) + 2,004 = 27,03

 

А 6,793 х + 0,007 х +  х = 7042

 

К 3,97 х + 20, 4 х + 0,63 х = 5050

 

Л ( 52,3 – х ) – 4,08 = 17,3

 

1006

30,92

3,6

202

14,374

10,2

 

4.. Итог урока.

Ну, вот и закончился рыцарский турнир.  Победитель  -

В ходе нашей игры мы повторили сложение и вычитание десятичных дробей, решение уравнений, построение точки на числовом луче.

Пора возвращаться домой из средневековья. Но чтобы вернуться, нужно разгадать анаграммы:

ТАМЕЛЬНАЗЕН (знаменатель)

ИЛЕТСИЧЛЬ(числитель)

ИНОЖЕЛЕС   (сложение)

ИВЕТЫЧАНИ(вычитание)

ОДАНОТИКАР(координата)

БОРЬД(дробь)

Молодцы!

1.                                                                          Домашнее задание (подготовиться к контрольной работе).

Самоанализ

Урок-игра «Рыцарский турнир» начинается с устной работы, где идет объяснение правил игры. Четко были сформированы тема, цели и тип урока. Все учащиеся были хорошо подготовлены  к уроку, легко включались в работу. На уроке использовалась наглядность, кодоскоп. Время было распределено рационально. Все учащиеся были вовлечены в работу. При помощи игр у детей автор развивала внимание, память, интерес к математике через использование различных видов заданий. Чередовались письменные виды деятельности с устными. За счет смены видов деятельности обеспечивалась высокая работоспособность учащихся на уроке. Урок был эмоционален и спокойно завершен.

Таким образом, применение дидактических игр на уроках помогает добиться того, чтобы каждый ученик работал активно и увлеченно, используя игру как отправную точку для возникновения и развития любознательности, глубокого  познавательного интереса. Подобранные игры способствуют развитию у учащихся памяти, внимания, наблюдательности, интереса. В этих играх важным стимулом является элемент соревнования, так как в соревнованиях проявляются активность ученика и воля к победе. Дидактические игры хорошо сочетались с серьезным учением.

 

2.2. Опытно-экспериментальная работа. Анализ ее результатов

 

Для подтверждения гипотезы и выполнения поставленных задач была проведена экспериментальная работа, которая проходила в три этапа:

1) Констатирующий эксперимент.

2) Формирующий эксперимент

3) Контрольный эксперимент.

Цель исследования: убедиться в эффективности использования различных видов дидактических игр для развития познавательного интереса на уроках математики.

Исследование проходило на базе МОУ «СОШ с. Старые Озинки». Были взяты два класса: 5 - экспериментальный и 6 – контрольный.

В 5 классе учатся 4 человека: 3 мальчиков и 1 девочек. Класс занимается по учебнику Мерзляка А.Г. .Математика 5 класс.

В 6 классе учатся 5 человек: 3 мальчиков и 2 девочек. Класс также занимается по учебнику Жохова В.И.  Математика 6 класс.

1. Констатирующий эксперимент.

Цель: выявить, на сколько дети активны и заинтересованы на уроках математики на исходном этапе эксперимента.

1.1. Анкетирование экспериментального класса

Учащимся была предложена следующая анкета:

Фамилия, имя

1) какой предмет в школе тебе больше всего нравится?

2) Ты быстрее решаешь устно или письменно?

3) Нравится ли тебе, когда на уроке математики проводят игры?

4) Тебе больше нравится выполнять задания по русскому языку, литературе или по математике?

5) На какой бы урок ты опоздал? (русский, математика, литература)

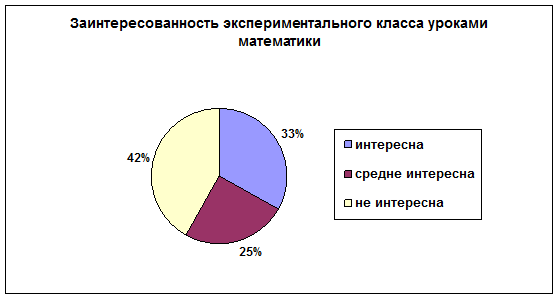
Основное внимание при анализе анкет учащихся уделялось 1 и 5 вопросам, 3 и 4, 2 вопросы дополняли ответ. Проанализировав протокол, были выявлены следующие результаты.[См.приложение 2]

При ответе на первый вопрос не всем учащимся нравятся уроки математики.  58% учащихся больше всего нравится математика, 9% - ИЗО, еще 9% нравится технология,12% нравится история и также 12% нравится русский язык. Таким образом, не всем учащимся легко заниматься математикой.

Результаты второго вопроса были следующими:  71% учащихся  быстрее решают устно, чем письменно; 29% учащихся быстрее решают письменно, чем устно.

Ответы на третий вопрос были такими: 90% учащихся нравится, когда с ними проводят игры, 10% - не нравится, когда с ними проводят игры.

Результаты четвертого вопроса были такими: 50% учащихся больше всего нравится выполнять задания по математике, 29% –нравится выполнять задания по русскому языку, 21% - нравится выполнять задания по литературе. Можно сказать, что половина учащихся этого класса не заинтересована в математике.

Ответы пятого вопроса: 33% учащихся – прогуляли бы математику, 46% - русский язык, 21% - прогуляли бы литературу.

Таким образом, у 33% учащихся экспериментального класса высокая заинтересованность в математике. Учащимся нравятся уроки математики, они активны на уроке, им нравится выполнять различные задания по математике, никогда бы не пропустили урок математики.

25% учащихся экспериментального класса имеет средний уровень заинтересованности в математике. На уроках учащиеся активны, но требуют систематических побуждений учителя. При разборе трудных вопросов прибегают к помощи учителя. Самостоятельное выполнение зависит от ситуации, наличия побуждения учителем или товарищем. Трудности преодолевают с помощью других.

У 42% учащихся экспериментального класса низкий уровень заинтересованности в математике.  Учащимся не нравятся уроки математики, наблюдается познавательн6я инертность. Не стремятся разобраться в трудных вопросах. Мнимая самостоятельность действий (списывание с доски, у соседа по парте), частые отвлечения. Полная бездеятельность при затруднениях, отсутствие интереса к математике.

 

 

1.2. Анкетирование контрольного класса.

 

Учащимся была предложена аналогичная анкета. Проанализировав протокол, были выявлены следующие результаты. [См. приложение 3]

При ответе на первый вопрос не всем учащимся нравятся уроки математики. 59% учащихся больше всего нравится математика, 10% - ИЗО, еще 12% нравится технология, 9% нравится история и 10% нравится русский язык. Таким образом, не всем учащимся легко заниматься математикой.

Результаты второго вопроса были следующими:  70% учащихся  быстрее решают устно, чем письменно; 30% учащихся быстрее решают письменно, чем устно.

Ответы на третий вопрос были такими: 92% учащихся нравится, когда с ними проводят игры, 8% - не нравится, когда с ними проводят игры.

Результаты четвертого вопроса были такими: 48% учащихся больше всего нравится выполнять задания по математике, 31% – нравится выполнять задания по русскому языку, 21% - нравится выполнять задания по литературе. Можно сказать, что половина учащихся этого класса не заинтересована в математике.

Ответы пятого вопроса: 35% учащихся – прогуляли бы математику, 45% - русский язык, 20% - прогуляли бы литературу.

Таким образом, у 34% учащихся контрольного класса высокая заинтересованность к математике. Учащимся нравятся уроки математики, они активны на уроке, им нравится выполнять различные задания по математике, они никогда бы не пропустили урок математики.

28% учащихся контрольного класса имеет средний уровень заинтересованности в математике. На уроках учащиеся активны, но требуют систематических побуждений учителя. При разборе трудных вопросов прибегают к помощи учителя. Самостоятельное выполнение зависит от ситуации, наличия побуждения учителем или товарищем. Трудности преодолевают с помощью других.

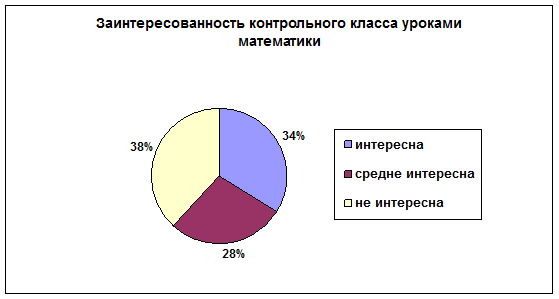
У 38% учащихся контрольного класса низкий уровень заинтересованности к математике. Учащимся не нравятся уроки математики, наблюдается познавательн6я инертность. Не стремятся разобраться в трудных вопросах. Мнимая самостоятельность действий (списывание с доски, у соседа по парте), частые отвлечения. Полная бездеятельность при затруднениях, отсутствие интереса к математике.

 

 

Таким образом, на развитие познавательного интереса  оказывает влияние возрастной аспект, поскольку приобретенные знания содействуют переводу интереса на более высокий уровень. Следует особенно подчеркнуть и то обстоятельство, что индивидуальное своеобразие познавательного интереса чрезвычайно велико. Учащиеся одного и того же класса могут находиться на самых различных, даже противоположных уровнях заинтересованности  уроками математики, что видно из диаграммы.

1.3. Анкетирование Григорьевой Т.М. и Ляляева С.Н. – учителей математики  5 и 6 классов.

Цель: выявить, как ведётся учителями работа по применению дидактических игр на уроках математики.

Учителям была предложена следующая анкета:

1) Проводите ли вы игры на уроках?

2) Если да, то, как часто (ответ подчеркнуть)

а – на каждом уроке

б – 3-4 раза в месяц

в – если остается лишнее время

3) На каком этапе урока проводятся вами дидактические игры? (ответ подчеркнуть)

а – при устном счете

б – при подготовке к изучению нового материала

в – при ознакомлении с новым материалом и при закреплении

г – при контроле знаний, умений и навыков

4) Что такое, по вашему мнению, познавательный интерес к предмету?

5) В чем состоит задача учителя в повышении интереса у учащихся к урокам математики?

 

	Григорьева Тамара Михайловна	Ляляев Сергей Николаевич
1 вопрос	Да	Да
2 вопрос	Если остается время на уроке	Если остается время
3 вопрос	При устном счете, при проверке знаний, умений и навыков	При устном счете
4 вопрос	Познавательный интерес побуждает к овладению знаниями, заставляет учеников работать, преодолевая трудности и препятствия	Познавательный интерес – это  понятие, суть которого заключается в стремлении учащихся к овладению знаниями
5 вопрос	Задача учителя состоит в эффективном использовании на уроках различных интересных моментов, в побуждении детей к изучению математики.	Использовать на уроках, игровые моменты, интересные задания с целью повышения  интереса.

 

Анализ анкет показал, что учителя используют на уроках математики игры, однако игры  проводятся не систематически из-за нехватки времени. В основном учителя используют игры при устном счете и при проверке и оценке знаний, умений и навыков. По мнению учителей, познавательный интерес – это понятие, суть которого заключается в побуждении к овладению знаниями, в стремлении учащихся работать, преодолевая трудности и препятствия. Задача учителя состоит в эффективном использовании на уроках математики игр, игровых моментов, в подборе к уроку интересных заданий с целью повышения интереса к уроку.

1.4 Наблюдение за работой учащихся на уроке математики

Цель: провести наблюдение и выяснить, на сколько дети экспериментального и контрольного классов активны  на уроках математики.

Критериями являлось: активная работа, частота правильных ответов, быстрота реакции, стремление достичь положительных результатов.

В графу «активен» заносились те ученики, которые активно работали на  протяжении всего урока, давали быстрые и правильные ответы,   

В графу «средне активны» заносились те ученики, которые работали только над теми заданиями, которые для них были легче и интереснее, поднимали реже руку, чтобы ответить, давали неверные ответы.

В графу «пассивен» заносились те ученики, которые постоянно отвлекались, не поднимали руку, чтобы ответить, неверно отвечали на вопросы.

Данные наблюдения занесены в протокол, в результате которого получено следующее. [См. приложение 4]

 

 

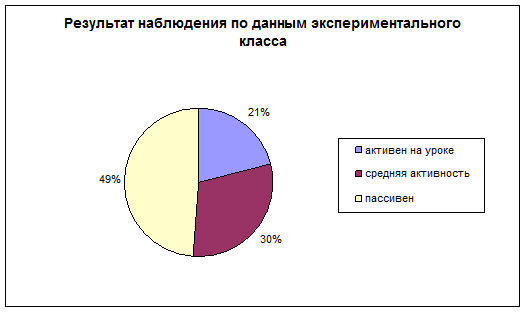
Таким образом, в исследовании принимало участие 24 человека, в результате которого выяснилось, что большая часть класса, а именно 49% не проявляют интереса к урокам математики, 30% проявляют частичный интерес в различных видах деятельности и лишь 21% активно участвуют в работе на уроках математики

Подобное наблюдение проводилось и  в контрольном классе. Данные наблюдения занесены в протокол, в результате которого получено следующее. [См. приложение 4]

 

 

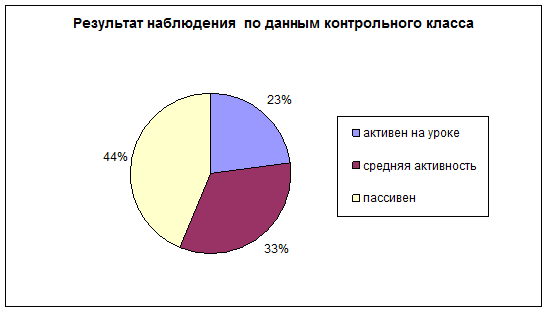
В исследовании принимали участие  18 человек. Результаты наблюдения по данным контрольного класса: 44% не проявляют активность на уроке математики, 33% частично активны на уроке и только 23% активно работают на уроке математики.

таблица 5 и 6 классов по данным наблюдения

 

На основании анкетирования и наблюдения учеников, можно сделать вывод, что интерес у детей экспериментального и контрольного классов на уроках математики не  высок.

1.5. Проверочная работа по теме «Обыкновенные дроби».

Цель: определить уровень вычислительных умений и навыков  после изучения темы «Обыкновенные дроби».

Учащимся 5а и 5б была предложена следующая контрольная  работа,   разработанная экспериментатором:

1.Найдите значение выражения

 

а) + -  ;б) 8 - (3 + 2);в)  (8- 7) + 3

 

2. В гараже 45 автомобилей. Из них  - легковые. Сколько легковых автомобилей в гараже?

3. Выполните действия:

 

а)  5 - 1; б)  3 + 1;   в)  5 + 5.

 

4. Решите уравнение: а)  3 - х = 1;    б) ( у - 8) + 1.

 

5. Какое число надо разделить на 8, чтобы частное равнялось 5?

Критерии оценки проверки работ:  За каждое правильное решенное задание дается 1 балл:

5 баллов – «5»отлично

4 балла  - «4»хорошо

3 балла  - «3»удовлетворительно

2 балла – «2»неудовлетворительно.

Проанализировав протоколы проверочной работы экспериментального и контрольного классов,  получены следующие результаты. [См. приложение 6,7]

 

 

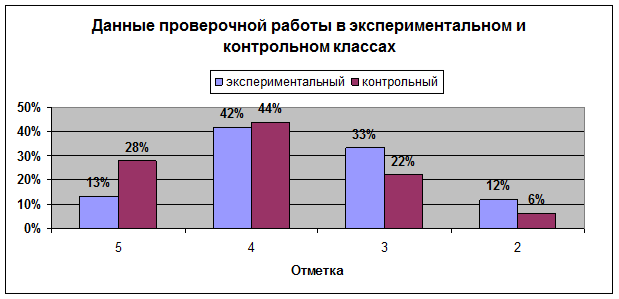
Таким образом, в результате сравнения полученных данных проверочной работы, выявлено, что контрольный класс находится на более высоком уровне сформированности вычислительных умений и навыков, чем экспериментальный класс.

Вывод: Констатирующий эксперимент показал, что:

-5 и 6 классы работают по одинаковой традиционной программе;

-классы примерно равны по возрастным показателям;

-интерес у классов на уроках математики не  высок;

-уровни сформированности вычислительных умений и навыков разные (экспериментальный класс отстает от контрольного класса).

На этой основе  сделан следующий вывод: что необходима коррекционная работа, направленная на развитие уровня познавательного интереса к математике, а также уровня усвоения знаний, умений и навыков вычислений при помощи проведения  работы с дидактическими играми в различных их видах и на разных этапах урока.

5 – экспериментальный класс, где будем проводить формирующий эксперимент,  6 – контрольный класс.

2. формирующий эксперимент.

Цель: повышение уровня познавательного интереса к урокам математики.

Задачи: - подобрать различные виды дидактических игр;

- способствовать повышению познавательного интереса к уроку математики;

- провести данные виды дидактических игр в экспериментальном классе.

На основе ранее перечисленных особенностей данного класса, с учетом содержания курса математики и возрастных особенностей учащихся, были взяты различные виды дидактических игр на разных этапах урока.

Цель дидактических игр: активизировать внимание детей на уроках математики, сделать процесс учения более интересным, развивать с помощью них познавательный интерес к уроку математики. Задания в занимательной форме более доступны и привлекательны для детей. Учащиеся незаметно для себя выполняют большее число арифметических действий, упражняются в устных вычислениях.

Дидактические игры проводились чаще всего в начале урока, чтобы привлечь внимание детей и подготовить их к усвоению последующего материала, или в конце урока, подводя итог нового материала, а также игре был посвящен целый урок. Использовалась безоценочная система знаний, поощрялись быстрота и правильность. Проведенные игры представлены в 2.1. Разработка конспектов уроков с использованием дидактических игр, их проведение и анализ.

Вывод: Проводимые виды дидактических игр  вызывали интерес у детей – они более активно работали на уроках, с готовностью выполняли задания учителя, стремились прийти к правильному результату. В процессе игры у детей вырабатывалась привычка сосредоточиваться, мыслить самостоятельно, развивалось внимание детей, стремление к знаниям. Увлекшись, дети не замечали, что учатся, познают, запоминают новое, ориентируются в необычных ситуациях, развивают фантазию. Дидактические игры очень хорошо уживаются с «серьезным» учением. Включение в урок дидактических игр и игровых моментов делало процесс обучения интересным и занимательным, создавало у детей бодрое рабочее настроение, облегчало преодоление трудностей в усвоении учебного материала. Проводя дидактические игры, особенный интерес вызывали у детей упражнения в занимательной форме.

3. Контрольный эксперимент.

В качестве контрольного эксперимента автор использовала наблюдение и контрольную работу по теме «Десятичные дроби. Сложение и вычитание десятичных дробей ».

Цель контрольного эксперимента состояла в выявлении наличия или отсутствия развития познавательного интереса к урокам математики, а так же выявление того, как это отразилось на уровне усвоения знаний, умений и навыков.

3.1. Наблюдение за работой учащихся на уроке математики

Цель: провести наблюдение и выяснить, на сколько дети экспериментального класса активны на уроках математики, чем дети контрольного класса.

Критериями являлось: активная работа, частота правильных ответов, быстрота реакции, стремление достичь положительных результатов.

В графу «активен» заносились те ученики, которые активно работали на протяжении всего урока, давали быстрые и правильные ответы,

В графу «средне активны» заносились те ученики, которые работали только над теми заданиями, которые для них были легче и интереснее, поднимали реже руку, чтобы ответить, давали неверные ответы.

В графу «пассивен» заносились те ученики, которые постоянно отвлекались, не поднимали руку, чтобы ответить, неверно отвечали на вопросы.

Данные о результатах наблюдения занесены в таблицу. [См. приложение 8]

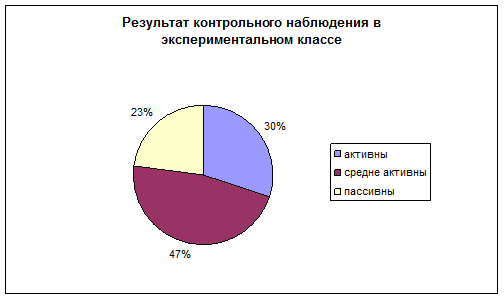
Таким образом, в исследовании принимало участие 24 человека, в результате которого выяснилось, что  30% учащихся активны  на уроках математики, 47% средне активны и лишь 23% пассивны на уроках математики.

Подобное наблюдение проводилось и  в контрольном классе. Данные о результатах наблюдения занесены в таблицу. [См. приложение 9]

 

 

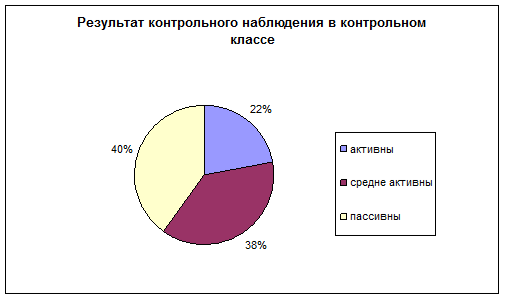
В исследовании принимали участие  18 человек. Результаты наблюдения по данным контрольного класса: 40% не проявляют активность на уроке математики, 38% частично активны на уроке и только 22% активно работают на уроке математики.

 

 

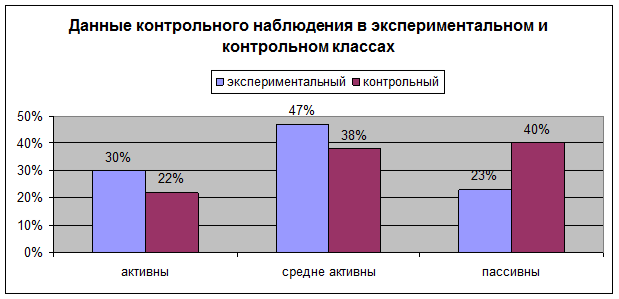
Как видно на диаграмме, учащиеся 5а класса после проведенного эксперимента стали более интересоваться уроками математики, это обусловлено тем, что проводилась работа на развитие познавательного интереса с помощью дидактических игр.

3.2. Контрольная работа по теме «Десятичные дроби. Сложение и вычитание десятичных дробей »

Цель: определить уровень сформированности вычислительных умений и навыков  после изучения темы «Десятичные дроби. Сложение и вычитание десятичных дробей» с использованием на уроках дидактических игр.

Учащимся 5 и 6 была предложена следующая контрольная  работа,   разработанная экспериментатором:

1. Сравните числа:    а) 7,189 и 7,2;   б) 0,34 и 0,3377;   в) 4,2 и 4,196.

2. Выполните действия: а) 61,35 - 49,561 – (2,69 + 4,01)  

б) 1000 – (0,72 + 81 – 3,968).  

3. Скорость теплохода по течению реки 42,8 км/ч. Скорость течения 2,8км/ч. Найдите собственную скорость теплохода и его скорость против течения.

4. Округлите числа: а) до сотых: 3,062; 4,137;  6,455;

б) до десятых: 5,86; 14,25; 30,22

в) до единиц: 247,57 и 376, 37.

Критерии оценки проверки работ: За каждое правильное решенное задание дается 1 балл:

4 балла – «5»отлично

3 балла  - «4»хорошо

2 балла  - «3»удовлетворительно

1 балл – «2»неудовлетворительно.

Данные по итогам контрольной работы зафиксированы в таблицу. [См. приложение 10,11]

 

 

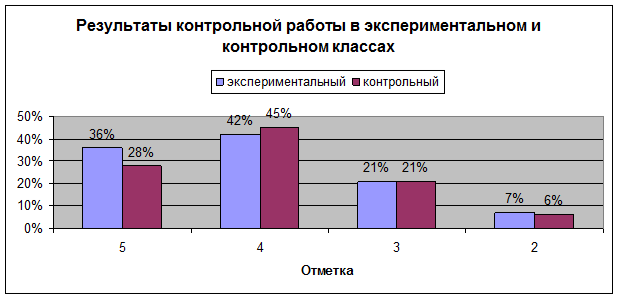
Таким образом, было выявлено, что вычислительные навыки сформированы лучше у детей экспериментального класса. Заметно развитие познавательного интереса к уроку математики, по сравнению с другим классом. В этом помогли дидактические игры.

Следовательно, дидактические игры помогли в развитии познавательного интереса, доказали свою эффективность – дети стали активнее и заинтересованнее заниматься на уроках математики. Дети, которые были пассивны на уроках, теперь с удовольствием вовлеклись в работу, активнее шли на контакт с учителем. Ученики соревновались друг с другом в сообразительности и быстроте ума. Используя дидактические игры,  учителю легче работать с отстающими детьми (осуществляется индивидуальный подход) – в игровой обстановке ребенок не боится отвечать, даже если не знает правильного ответа.

Игра стимулирует умственную деятельность учащихся, развивает внимание и познавательный интерес к предмету. Игра – один из приемов преодоления пассивности учеников. Игра воспитывает у школьников дисциплинированность, ответственность и коллективизм.

Заключение

 

В данной работе рассмотрен особый вид игр — дидактические игры, особая форма занятий - игровая форма. Из изложенного выше можно сделать вывод, что дидактическая игра отличается от обыкновенной игры тем, что участие в ней обязательно для всех учащихся. Ее правила, содержание, методика проведения разработаны так, что для некоторых учащихся, не испытывающих интереса к математике, дидактические игры могут послужить отправной точкой в возникновении  познавательного интереса. Основным в дидактической игре на уроках математики является обучение математике. Игровые ситуации лишь активизируют деятельность учащихся, делают восприятие более активным, эмоциональным, творческим. Поэтому использование дидактических игр дает наибольший эффект в классах, где преобладают ученики с пониженным интересом к предмету, для которых математика кажется скучной и сухой наукой. Создание игровых ситуаций на уроках математики повышает интерес к математике, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность, чувство соревнования, взаимопомощь. Мною  изучено 25 источников учебно-методической литературы, подобрано 12 игр по теме «Сложение и вычитание десятичных дробей» в 5 и 6 классе и проанализировано 12 конспектов по данной теме. Изучив более подробно и глубоко вопросы, связанные с использованием дидактических игр на уроках, поставленные цели и задачи решены. Гипотеза дала положительный результат.

Использование дидактических игр на разных этапах изучения математического материала является эффективным средством активизации учебной деятельности школьников, положительно влияющим на повышение качества знаний, умений и навыков учащихся, развитие умственной деятельности. Данная работа может стать методическим пособием для студентов КПУ, как при подготовке докладов, сообщений на эту тему, так и при проведении пробных уроков математик

Литература

 

1.Автайникова, А.К. Некоторые формы организации устного счета // Математика в школе. – 2001.- №3.- 123с.

2.Ананьев, Б.Г. Познавательные потребности и интересы. – Л.,2002.-243с.

3.Бабкина, Н.В. Использование игр и упражнений в учебном процессе // Начальная школа. – 1988.-№4.-56с.

4.Бондаренко, А.К., Матусин А.И. Воспитание в игре. – М.: Просвещение, 1983.- 192с.

5.Бряшина, Н. Математический брейн-ринг // Математика.-2003.-№27.-31с.

6.Газман, О.С., Харитонова Н.Е. В школу с игрой. – М.: Просвещение, 1991.- 96с.

7.Данилов, И.К. Об игровых моментах на уроках математики // Математика в школе. – 2005.- №1.- 98с.

1.                 Демченкова, Н., Моисеева Е. Формирование познавательного интереса у учащихся // Математика. -2004.- №19. – 30с.

2.                 Зимний, О.В. Элементы игры на уроках // Математика в школе. – 2004.- №6.- 87с.

3.                 Коваленко, В.Г. Дидактические игры на уроках математики. – М.: Просвещение, 1990. –  95с.

4.                  Коконов, А.Я. Устные занятия по математике 5-9 классы: Пособие для учителей. – М.: Издательский дом «Генжер», 1998.- 80с.

5.                 Кордемский, Б.А. Математическая смекалка. - М.: Просвещение, 1981.- 575с.

6.                  Кордемский, Б.А. Увлечь школьников математикой.– М., 1981.- 371с.

7.                  Крутецкий, В.А. Психология: Учебник для учащихся педагогических училищ.- М.: Просвещение, 2000.- 345с.

8.                  Минаева, С.С. Вычисления на уроках и внеклассных занятиях по математике: Пособие для учителя.- М.: Просвещение, 1983.- 128с.

9.                  Минскин, Е.М. От игры к занятиям. – М.: Просвещение, 1982.- 192с.

10.              Ожегов, С.И., Шведова Н.Ю. Толковый словарь русского языка. - 4-е изд., дополненное. М., 1997. – 876с.

11.              Ситников, Т.В. Приемы активизации учащихся в 5-6 классах //  Математика в школе. – 2003. -№2.- 32с.

12.             Спивановская, А.С. Игра – это серьезно. – М.: Педагогика, 1981.- 123с.

13.              Стеблина, Б. Игровые формы занятий 5-6 классы // Математика. – 2001.- №23.- 32с.

14.              Финько, З. Игровые уроки 5-6 классы // Математика. – 2001. - №23. – 34с.

15.              Шмаков, С.А. Игры учащихся – феномен культуры. – М.: Новая школа, 1994. – 240с.

16.              Шмаков, С.А. Культура – досуг – ребенок. – М.: Просвещение, 1994. – 381с.

17.              Щукина, Г.И. Активизация познавательной деятельности учащихся в учебном процессе: Учебное пособие для студентов педагогических институтов. – М.: Просвещение, 1980. – 156с.

18.             Шукина, Г.И. Актуальные вопросы формирования интереса в обучении: Учебное пособие для студентов педагогических институтов. – М.: Просвещение, 1980. – 245с.

Приложение 1

Уровни развития познавательного интереса
Высокий	Средний	Низкий
Высокая познавательная самопроизвольная активность	Познавательная активность, требующая систематических побуждений учителя	Познавательная инертность
Интерес к сущности явлений и процессов, к их взаимосвязям и закономерностям. Стремление разобраться в трудных вопросах.	Интерес к накоплению информации, в основе которой лежат факты, описания. Понимание сущности познания только при помощи учителя	Эпизодический интерес к эффектным занимательным сторонам явлений при отсутствии интереса к их сущности.
Интенсивно, с увлечением протекающий процесс самостоятельной деятельности.	Зависимость процесса самостоятельной деятельности от ситуации, наличия побуждений.	Мнимая самостоятельность действий (списывание с доски, у соседа по парте), частые отвлечения.
Стремление к преодолению трудностей.	Преодоление трудностей с помощью других, ожидания помощи.	Полная бездеятельность при затруднениях.
Посвящение свободного времени предмету интереса.	Эпизодические занятия предметом интереса.	Отсутствие склонности к какому-либо виду деятельности

 

Приложение 2

Протокол анкетирования экспериментального класса

Фамилия, Имя	1 вопрос	2 вопрос	3 вопрос	4 вопрос	5 вопрос
Сулин Данила	Математика	Устно	Да	Математике	Литература
Кулибабин Багдан	Изо	Устно	Да	Литературе	Математика
Уразаков Камиль	История	Устно	Да	Литературе	Математика
Арестанова Элина	Русский	Устно	Нет	Русскому	литературу

Приложение 3

Протокол анкетирования контрольного класса

Фамилия Имя	1 вопрос	2 вопрос	3вопрос	4 вопрос	5 вопрос
Байбусинов Асланбек	Математика	Устно	Да	Математике	Русский
Туйгушев Эмиль	Изо	Устно	Да	Русскому	Математика
Залазаев Юра	Технология	Устно	Да	Литературе	Математика
Брызгалова Анжелика	Математика	Письменно	Да	Математике	Русский
Брызгалова Елена	История	Устно	Нет	Русскому	Математика

Приложение 4

Протокол наблюдения  экспериментального класса

Фамилия	Устныйсчет	Изучение нового материала	Закрепление изученного материала
Сулин	+	+	-	Средне активна
Уразаков	+	+	+	Активна
Кулибабин	+	+	+	Активна
Арестанова	-	-	-	Пассивен

 

Приложение 5

Протокол  наблюдения  контрольного класса

Фамилия	Устный счет	Изучение нового материала	Закрепление изученного материала
Байбусинов	+	-	+	Средне активен
Туйгушев	+	+	+	Активен
Залазаев	+	+	+	Активна
Брызгалова А	+	+	+	Активен
Брызгалова Е	-	-	-	Пассивен

Приложение 6

Протокол проверочной работы экспериментального класса

Фамилия	№1	№2	№3	№4	№5	Отметка
Сулин	+	+	+	+	-	4
Уразаков	+	+	+	+	+	5
Кулибабин	+	-	+	+	+	4
Арестанова	+	-	-	-	+	2

Приложение 7

Протокол проверочной работы контрольного класса

Фамилия	№1	№2	№3	№4	№5	Отметка
Байбусинов	+	+	+	-	+	4
Туйгушев	+	+	+	+	+	5
Залазаев	+	+	+	+	+	5
Брызгалова А	+	+	+	+	+	5
Брызгалова Е	+	-	+	-	-	2

 

Приложение 8

Протокол  контрольного наблюдения экспериментального класса

Фамилия	Устныйсчет	Изучение нового материала	Закрепление изученного материала
Сулин	+	+	+	Активна
Уразаков	+	+	+	Активна
Кулибабин	+	+	+	Активна
Арестанова	+	+		Средне активен

 

Приложение 9

Протокол контрольного наблюдения контрольного класса

Фамилия	Устный счет	Изучение нового материала	Закрепление изученного материала
Байбусинов	+	-	+	Средне активен
Туйгушев	+	+	+	Активен
Залазаев	+	+	+	Активна
Брызгалова А	+	+	+	Активен
Брызгалова Е	-	-	-	Пассивен

 

Приложение 10

Протокол контрольной работы экспериментального класса

 

Приложение 11

Протокол контрольной работы контрольного класса