ЛАБОРАТОРНАЯ РАБОТА № 2. ИЗУЧЕНИЕ МНОГОСЛОЙНОГО НЕЛИНЕЙНОГО ПЕРСЕПТРОНА И АЛГОРИТМА ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ

Лабораторная работа № 2. ИЗУЧЕНИЕ МНОГОСЛОЙНОГО НЕЛИНЕЙНОГО ПЕРСЕПТРОНА И АЛГОРИТМА ОБРАТНОГО РАСПРОСТРАНЕНИЯ ОШИБКИ

1 ЦЕЛЬ РАБОТЫ

Изучить возможности многослойного персептрона как аппроксиматора и классификатора.

2 СВЕДЕНИЯ ИЗ ТЕОРИИ

2.1 Алгоритм обратного распространения ошибки

Пусть определена трехслойная нейронная сеть с п входами, m выходами и l скрытыми между ними элементами, тогда необ­ходимо рассмотреть и построить два слоя весов: от входов к скрытым элементам и к выходу, т. е. (W₁, W₂).

Назначение алгоритма обратного распространения ошиб­ки – настройка всех слоев многослойной структуры. Рас­смотрим работу алгоритма на примере сети с одним скрытым слоем и одним выходом (рис. 5). Преобразования вход­ных сигналов, задаваемые нейронной сетью, определяются следующими формулами:

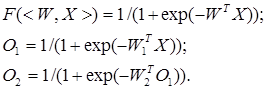
Общая функция ошибки зависит от весов всех слоев, в на­шем случае от вектора W₂ и от матрицы W₁:

где Y – выход, который задан в обучающей выборке.

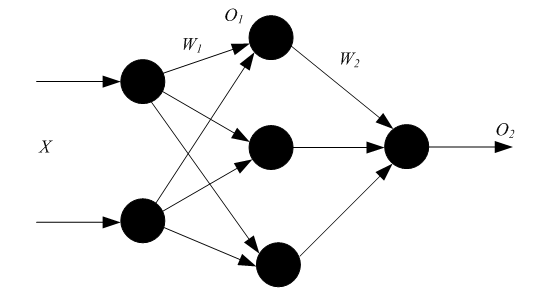
Рис. 5. Многослойный персептрон

Теперь необходимо определить приращение каждого веса с помощью частных производных:

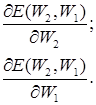
Для многослойной архитектуры частные производные ошибки по матрице весов каждого слоя определяются по формуле сложной производной. В случае униполярной сигмоиды правило изменения весов будет следующим:

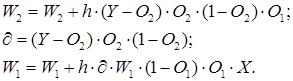
Таким образом, метод обратного распространения ошибки позволяет из­менять веса промежуточных слоев, хотя желаемые значения на промежуточных слоях не заданы.

2.2 Описание основных функций

Функция newff создает нейронную сеть прямого распрост­ранения сигнала, обучаемую с помощью алгоритма обратного распространения ошибки:

net = newff(PR, [S1 S2 SNl], {TF1 TF2 TFNl), BTF, BLF, PF).

Рассмотрим параметры функции newff: PR – матрица ин­тервалов значений для R входных элементов, задаваемых ми­нимальным и максимальным значениями; S_i – размер i-го слоя, для N слоев; TF_i – функция активации i-го слоя, по умолчанию используется функция tansig – гиперболический тангенс; BTF – функция обучения сети методом обратного распространения ошибки, по умолчанию используется функ­ция traingdx; BLF – функция изменения весов при обучении, по умолчанию используется learngdm; PF – функция измере­ния ошибки, по умолчанию тsе. Функция newff возвращает многослойную нейронную сеть прямого и обратного распро­странения сигнала и ошибки соответственно. Функции акти­вации могут быть выбраны из следующего перечня: гипербо­лический тангенс tansig, логистическая сигмоида logsig или линейная функция purelin.

3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

ПРИМЕР 1 Создание и обучение нейронной сети с по­мощью алгоритма обратного распространения ошибки

Зададим с помощью графика исходную функцию:

% входы НС

P = [0 1 2 3 4 5 6 7 8];

% желаемые реакции НС

T = [0 0.44 0.88 0.11 -0.66 -0.95 -0.45 0.18 0.92];

% изображение аппроксимируемой функции

plot(P, T, 'o');

Используем функцию newff, чтобы создать двухслойную сеть прямого распространения. Пусть сеть имеет входы с интервалом значений от 0 до 8, первый слой с 10 нелинейными сигмоидальными, второй – с одним линейным нейронами. Используем для обучения алгоритм обратного распространения ошибки (backpropagation) Левенберга – Марквардта (рис. 6).

% создание двухслойной НС прямого распространения с интервалом

% значений входов от 0 до 8, причем первый слой содержит

% 10 нелинейных сигмоид, а второй — один линейный нейрон.

% Для обучения используется алгоритм обратного распространения

% ошибки (backpropagation).

net = newff([0 8], [10 1], {'tansig' 'purelin'},'trainlm');

% имитация работы необученной НС

yl = sim (net, P);

% изображение результатов работы необученной НС

plot(P, T, 'o', P, yl, 'x') ;

% Обучим сеть на 100 эпохах с целевой ошибкой 0.01:

% установка количества проходов

net.trainParam.epochs = 50;

% установка целевого значения ошибки

net.trainParam.goal = 0.01;

% обучение НС (рис. 6)

net = train(net, P, T) ;

% имитация работы обученной НС

y2 = sim(net,  P);

% изображение результатов работы НС (рис. 7)

plot(P, T, 'o', P, yl, 'x', P, y2, '+');

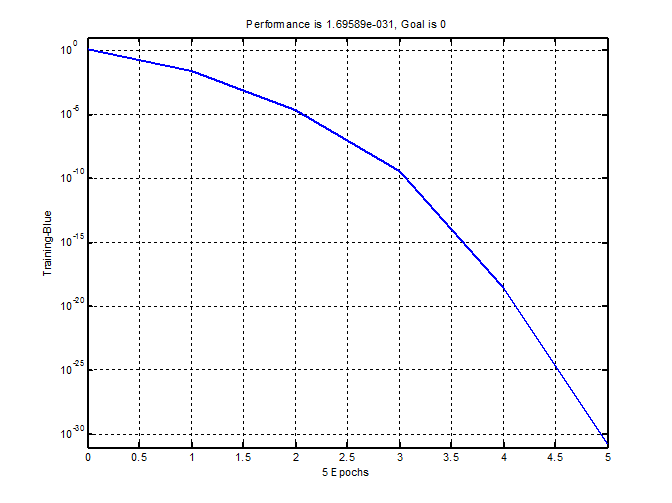
Рис. 6. График обучения двухслойного персептрона

Для исследования работы алгоритма обратного распространения ошибки воспользуемся примером, встроенным в Matlab toolbox, набрав команду demo.

В появившемся диалоговом окне необходимо последовательно выбирать пункты меню: Toolboxes->Neural Network->Other Demos->Other Neural Network Design textbook demos->Table of Contents->10-13->Backpropagation Calculation.

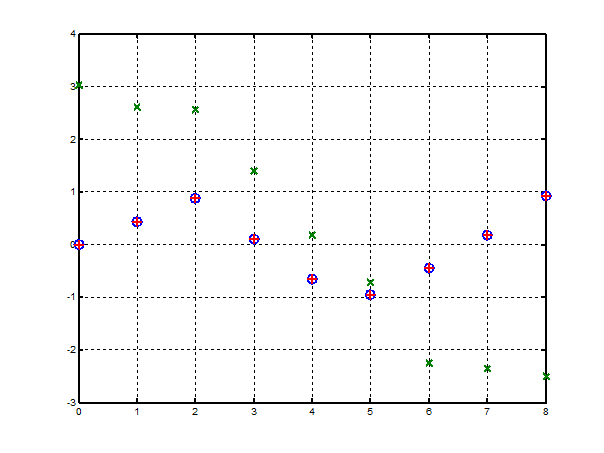
Рис. 7. Результат аппроксимации векторов двухслойным персептроном

В примере используется двухслойный персептрон с двумя нелинейными нейронами в первом слое и одним во втором. Действие алгоритма обратного распространения ошибки разбито на следующие шаги: назначение входа и желаемого вы­хода, прямой проход входного сигнала до выхода, обратное распространение ошибки, изменение весов. Переменные, по­зволяющие проследить работу алгоритма обратного распро­странения ошибки, обозначены следующим образом:

Р – входной сигнал;    

W₁(i) – вектор весов первого слоя, W₁(1) – вес связи, пе­редающий входной сигнал на первый нейрон, a W₁(2) – на второй;

W₂(i) – вектор весов второго слоя, W₂(1) – вес связи, пе­редающий входной сигнал с первого нейрона во второй слой, a W₂(2) – со второго;

B₁(i) – вектор пороговых значений (bias) нейронов пер­вого слоя, i = 1, 2;

В₂ – пороговое значение (bias) нейрона второго слоя;

N₁(i) – вектор выходов первого слоя, i = 1, 2;

N₂ – выход второго слоя;

A₁(i) – вектор выходных сигналов первого слоя после вы­полнения функции активации (сигмоиды), i = 1, 2;

А₂ – выход второго слоя после выполнения функции ак­тивации (линейной);

lr –  коэффициент обучаемости.

Пусть входной сигнал Р = 1,0, а желаемый выход .

Результаты выполнения этапов алгоритма представлены в табл. 1.

Таблица  1

Результаты поэтапного выполнения алгоритма обратного распространения ошибки

4 КОНТРОЛЬНЫЕ ВОПРОСЫ

1.                 Каким алгоритмом обучают многослойные НС?

2.                 Из каких основных этапов состоит алгоритм обратного распространения ошибки?

3.                 Почему алгоритм обратного распространения ошибки от­носится к классу алгоритмов градиентного спуска?

4.                 Как влияет функция принадлежности на правило измене­ния весов в обратном алгоритме распространения ошибки?

5.                 Какая функция в среде MATLAB создает НС прямого распространения?

6.                 Какие функции активации могут быть назначены для нейронов НС прямого распространения?

Скачано с www.znanio.ru