Добавить материал

и получить 10 документов
и свидетельство автора

Шибеко Марина Николаевна

Лекция 5. Экономика информационной безопасности на примере оценки криптосистем

doc
26.04.2020

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

0203. Лекция 5. Экономика информационной безопасности на примере оценки криптосистем.doc

Лекция 5. Экономика информационной безопасности на примере оценки криптосистем

Цель лекции

· Рассмотреть преимущества и недостатки существующих методов обоснования инвестиций в средства обеспечения ИБ;

· Выделить набор финансово-экономических показателей для оценки эффективности СКЗИ с экономических позиций

· Изучить методику экономической оценки эффективности СКЗИ

Текст лекции

Важность экономического обоснования инвестиций в ИБ подчеркивал В.Мамыкин, директор по информационной безопасности кабинета президента Microsoft в России и СНГ, в своих выступлениях на конференциях Security @ Interop '2008 и IT-Summit'2008 [7.48]. Согласно [7.49], большинство зарубежных компаний (84%) используют ROI и другие инструменты для оценки инвестиций в ИБ, которые составляют в среднем 5% всего ИТ-бюджета. В России на ИБ идет 0,5% ИТ бюджета, т.е. в 10 раз меньше. Такую ситуацию В.Мамыкин напрямую связывает с тем, что в нашей стране пока не получила широкого распространения практика оценки эффективности средств обеспечения ИБ с экономических позиций.

Расчет финансово-экономических показателей СЗИ позволяет решить следующие задачи [7.47]:

· Обоснование внедрения системы по обеспечению информационной безопасности на предприятии с экономической точки зрения;

· Оценка экономической эффективности внедрения или замены системы безопасности информации;

· Прогнозирование расходов по созданию/ функционированию/ модернизации СЗИ (задача управления бюджетом);

· Сравнение по экономическим критериям нескольких вариантов создания СЗИ, построенных на различных архитектурах (системах и компонентах), с целью выбора оптимального варианта реализации проекта (задача выбора ИТ-стратегии).

Качество информации, необходимой для принятия решения о целесообразности инвестиций, в первую очередь, будет зависеть от исходных данных, на основе которых производились вычисления. Уязвимым местом в любой методике расчета является именно сбор и обработка первичных данных, их качество и достоверность. Одним из основных вопросов является оценка затрат на ИБ. Выбор необходимой степени защиты должен учитывать ряд критериев: уровень секретности информации; ее стоимость; время, в течение которого она должна оставаться в тайне и т.д. Известный криптограф Брюс Шнайер (Bruce Schneier) в работе [7.26] подчеркивает, что термин "безопасность" лишен смысла без сведений о том, от кого и на какой срок защищена информация. Это утверждение применимо как к системам обеспечения безопасности в целом, так и к их важнейшему компоненту - средствам криптографической защиты информации.

Средства криптографической защиты информации (СКЗИ) представляют собой средства вычислительной техники, осуществляющие криптографическое преобразование информации для обеспечения ее безопасности. Росс Андерсон (Ross J Anderson), ведущий эксперт в области информационной безопасности, в своей статье [7.3] приходит к выводу, что при оценке уровня защищенности специалист должен принимать во внимание не только технические характеристики криптосистемы, получаемые путем криптоанализа и анализа информационных потоков, но использовать также и экономические инструменты.

Рассмотрим возможность разработки методики анализа эффективности СКЗИ с учетом того, каким угрозам защищаемая информация будет подвергаться со стороны злоумышленников.

Для решения поставленной задачи необходимо:

· формализовать процесс оценки эффективности криптографической защиты;

· разработать математическую модель угроз безопасности информационных ресурсов, защищенных с использованием криптографических средств;

· обеспечить криптоаналитика набором инструментальных средств, позволяющих оценить стойкость криптографических средств по отношению к идентифицированным угрозам;

· провести анализ существующих методов оценки СКЗИ с экономических позиций и выбрать финансово-экономические показатели, подходящие для экономической оценки инвестиций в СКЗИ.

Поставленные цели согласуются с задачами, вошедшими в перечень основных направлений и приоритетных проблем научных исследований в области информационной безопасности Российской Федерации, который был разработан секцией по информационной безопасности Научного совета при Совете Безопасности Российской Федерации при активном участии ведущих ученых и специалистов научных учреждений и организаций РАН, вузов, федеральных органов исполнительной власти, работающих в различных областях, связанных с обеспечением национальной безопасности (см. [7.44], пп. 46, 47 и 56).

Процесс оценки эффективности криптографической защиты

Анализ существующих подходов

При оценке эффективности СКЗИ важнейшим критерием считается криптостойкость, т.е. способность противостоять атакам криптоаналитика [7.40]. Такой подход не учитывает других важных требований к криптосистемам, а именно (см. [7.46]):

· минимальный объем используемой ключевой информации;

· минимальная сложность реализации (в количестве машинных операций);

· стоимость;

· высокое быстродействие.

Кроме того, использование СКЗИ, обеспечивающих устойчивость к взлому ниже некоторой "фоновой" вероятности, является экономически неоправданным [7.35]. Например, если вероятность выхода компании из бизнеса равна 2³⁰ (менее чем один из миллиона), то есть ли смысл для защиты информации, которая может нанести компании ущерб, сопоставимый с кризисом рынка, использовать алгоритм, вероятность вскрытия которого за приемлемое время составляет 2¹⁰⁰?

В статье В.П.Иванова [7.38] эффективность криптографических средств защиты предлагается оценивать с использованием математического аппарата теории массового обслуживания и теории катастроф на основе вероятностно-временной группы показателей, в числе которых:

· среднее время безопасного функционирования защищаемой системы;

· время безопасного функционирования защищаемой системы с вероятностью НСД не выше заданной;

· экономическая эффективность созданной системы защиты информации.

Выбор показателей эффективности представляет интерес, однако методика имеет ряд критических недостатков, которые делают невозможным ее применение на практике для оценки современных СКЗИ. В первую очередь это границы применимости: методика подходит только для оценки криптосистем, принадлежащих по классификации Ж.Брассара (Gilles Brassard) [7.6] к классу криптосистем ограниченного использования, стойкость которых основывается на сохранении в секрете алгоритмов зашифрования и расшифрования. Однако, согласно фундаментальному допущению Кирхгоффа (Auguste Kerckhoffs) [7.14], стойкость криптосистемы должна основываться не на секретности алгоритмов зашифрования и расшифрования, а на секретности некоторого значения, которое называется ее ключом. Все современные криптосистемы построены по этому принципу, и исследования их надежности всегда должны проводиться в предположении, что потенциальному противнику о криптосистеме известно все, за исключением используемого ключа.

Еще одним недостатком методики, описанной в работе [7.38], является то, что она не учитывает зависимости эффективности криптосистемы от условий ее использования. Очевидно, эффективность одной и той же криптосистемы в разных контекстах может существенно отличаться, т.к. среда функционирования системы накладывает определенные ограничения на возможные сценарии атак.

Существуют методики, позволяющие построить модели угроз и уязвимостей информационных систем и на основе анализа рисков получить количественную оценку соотношения потерь от угроз безопасности и затрат на создание системы защиты (см., например, [7.39]):

· метод CRAMM, разработанный Агентством по компьютерам и телекоммуникациям Великобритании по заданию Британского правительства [7.9];

· семейство программных продуктов RiskWatch от одноименной американской компании [7.23];

· комплексная система анализа и управления рисками информационной системы ГРИФ, созданная отечественной компанией Digital Security [7.10].

Эти инструментальные средства полезны специалисту при проведении аудита систем обеспечения безопасности предприятия, однако они не учитывают специфики СКЗИ и, как показано в [7.34], не подходят для решения поставленной в данной работе задачи.

Наконец, существуют методы формального анализа криптопротоколов. Криптографический протокол [7.24] регламентирует последовательность действий, выполняемых двумя и более сторонами для решения какой-либо задачи с использованием криптографических преобразований и алгоритмов. Можно выделить три основных класса методов анализа криптопротоколов:

· Дедуктивные методы, основанные на автоматическом доказательстве теорем, связанных со свойствами исследуемого криптопротокола [7.5];

· Методы анализа состояний, моделирующие криптопротокол в виде конечного автомата [7.4];

· Методы статического анализа, объектом исследования в которых являются потоки данных и управления [7.7].

Перечисленные подходы имеют существенный недостаток: все они построены на предположении, что используемые в протоколе криптографические примитивы идеальны. Рассматривается только концептуальная схема протокола, от конкретных методов шифрования и их подверженности атакам злоумышленника принято абстрагироваться.

Модель процесса оценки эффективности СКЗИ

Наиболее эффективным при выборе и оценке криптографической системы считается использование экспертных оценок [7.46]. При оценке эффективности СКЗИ необходимо принимать во внимание взаимосвязь факторов, определяющих ее подверженность атаке определенного типа. Упрощенное графическое представление модели сценария атаки изображено на рис. 7.1. Во избежание избыточности из модели исключен элемент "Защищаемые ресурсы", который задается неявно - через элемент "Злоумышленник" (характер зашифрованной информации определяет возможных злоумышленников, которые могут осуществлять попытки взлома в целях нарушения конфиденциальности, целостности или доступности).

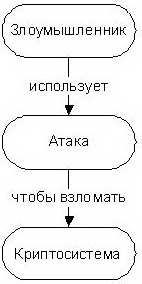
Модель сценария взлома

Рис. 7.1. Модель сценария взлома

На основании предложенной модели сценария атаки построена модель угроз безопасности информационных ресурсов из трех элементов [7.30] - ABC-модель ("A" от англ. Attack - атака, "B" от англ. code-Breaker - взломщик шифра, "C" от англ. Cryptosystem - криптосистема ). Математическое описание ABC -модели дано позже, здесь мы рассмотрим процесс экспертной оценки эффективности криптографической защиты (графическая модель процесса изображена на рис. 7.2).

Целью этапов 1-3 является построение ABC -модели. Первый этап - определение объекта исследования. Здесь описываются конкретные характеристики криптосистемы. На втором этапе задаются параметры, определяющие тип потенциальных взломщиков криптосистемы. Как будет показано в следующем разделе, при наличии формальных представлений исследуемой криптосистемы и потенциальных злоумышленников мы можем перейти к третьему этапу, т.е. определить типы атак, которым подвержена криптосистема, а также связанный с ними риск.

Четвертый этап представляет собой анализ устойчивости криптосистемы к атакам, определенным на третьем этапе. Для проведения криптоанализа специалиста необходимо обеспечить набором инструментальных средств, исследование и разработке которых будет рассмотрена далее.

Наконец, пятый этап предполагает использование различных подходов к оценке экономической эффективности инвестиций в СКЗИ на основании данных, полученных на этапах 1-4.

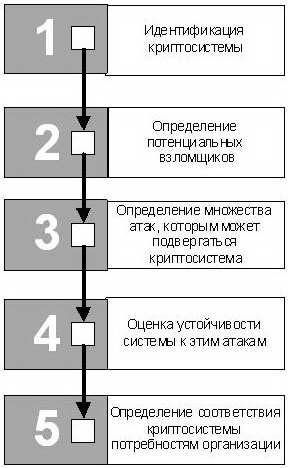
Процесс оценки эффективности криптографической защиты

Рис. 7.2. Процесс оценки эффективности криптографической защиты

Моделирование угроз безопасности информационных ресурсов

Задача состоит в разработке ABC -модели угроз безопасности информационных ресурсов, защищенных с использованием криптографических средств, которая даст возможность формализовать взаимосвязь между параметрами криптосистемы, потенциальных злоумышленников и возможных атак. Для решения поставленной задачи необходимо:

· Разработать многокритериальные классификационные схемы, позволяющие идентифицировать:

o криптосистему - с учетом особенностей ее реализации;

o потенциального взломщика - с учетом его мотивации, возможностей и квалификации;

o криптоаналитическую атаку - с учетом применимости к различным криптосистемам и необходимых для ее осуществления ресурсов.

· На основе разработанных классификаций создать параметрические модели криптосистем, атак и злоумышленников;

· Установить зависимость возможных сценариев взлома от характеристик злоумышленников и от особенностей реализации исследуемой криптосистемы.

Анализ существующих подходов

Для идентификации исследуемой криптосистемы нужно выделить набор ее ключевых свойств. Известны классификации криптосистем, в числе которых - классификационная схема, предложенная швейцарским математиком и криптографом У.Маурером (Ueli Maurer) [7.21] и основанная на том, чтобы различать криптосистемы по количеству ключей, упомянутая выше схема Ж.Брассара [7.6], в которой криптосистемы различаются в зависимости от сохранения в секрете механизма шифрования. Ни одна из этих классификаций сама по себе не позволит идентифицировать криптосистему - необходима многокритериальная классификация. С этой точки зрения представляет интерес работа К.Черезова [7.43], в которой предлагаются обобщающие критерии для сравнения продуктов на российском рынке СКЗИ:

· Фирма-производитель;

· Тип реализации;

· Наличие действующих сертификатов соответствия ФСБ России и классы защиты;

· Реализованные криптографические алгоритмы;

· Поддерживаемые операционные системы;

· Предоставляемый программный интерфейс;

· Наличие реализации протокола SSL / TLS ;

· Поддерживаемые типы ключевых носителей;

· Интегрированность с продуктами и решениями компании Microsoft ;

· Наличие дистрибутива продукта в свободном доступе на сайте производителя, дилерской сети распространения и сервиса поддержки.

Недостатком приведенной классификации для построения параметрической модели криптосистемы является то, что для решения поставленной в нашей работе задачи важны не "потребительские" и "технические" характеристики СКЗИ, а их свойства, определяющие подверженность тем или иным атакам.

Типы взломщиков, от которых криптосистема должна обеспечить защиту, определяют разумный уровень безопасности. Чтобы понять, каким атакам будет подвергаться система, необходимо выделить наиболее вероятных взломщиков. Классификации Дж.Говарда (John D Howard) [7.13] и Б.Шнайера [7.25], в которых злоумышленники различаются в зависимости от их движущих мотивов, подходят для высокоуровневого анализа контекста использования криптосистемы, однако не позволяют установить зависимость возможных сценариев атак от характеристик злоумышленников.

Существует большое количество классификаций и таксономий атак. Недостатком схем, описанных в [7.15, 7.17, 7.22, 7.28], является то, что они разработаны для описания атак на компьютерные системы, а объектом нашего исследования является более узкий класс атак - криптоаналитические атаки. Классификация Кирхгоффа [7.14] по доступу к открытому и зашифрованному тексту с появлением атак по побочным каналам [7.37] уже не может считаться полной; кроме того, она не позволяет учитывать такие важные факторы, как объем необходимых ресурсов, возможность распараллеливания и т.д.

Математическая модель угроз безопасности информационных ресурсов

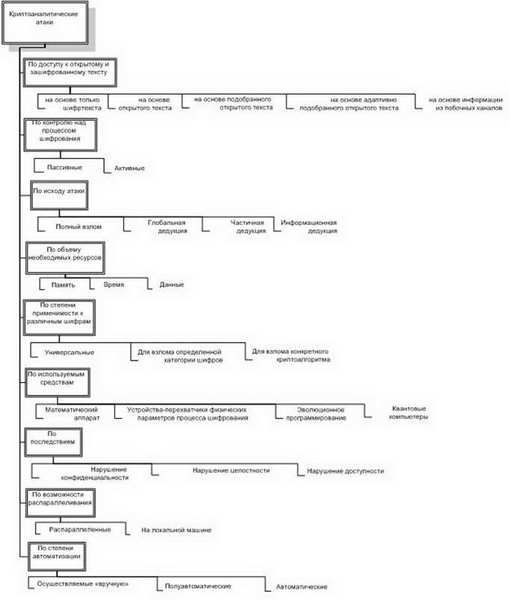
На основе анализа существующих классификационных схем, перечисленных выше, нами были разработаны новые многокритериальные классификации криптосистем, атак и злоумышленников (см. рис. 7.3 - 7.5 ). Далее мы покажем, как применение разработанных классификационных схем для построения ABC -модели позволяет провести всесторонний анализ угроз безопасности информационных ресурсов, защищенных с использованием криптографических средств.

Пусть $A \subseteq A_1 \times A_2 \times \ldots \times A_8$ - множество параметрических моделей атак, где ( $i=\overline{1,9}$ ) - множество значений i-го параметра модели атаки, определяющего тип атаки в соответствии с критериями разработанной классификации. Каждая модель $\vec a \in A$ представляет собой вектор $(a_1, a_2, \ldots , a_9)$ , где $\vec {a_i} \in A_i$ .

Аналогично, параметрическая модель злоумышленника задается в виде вектора $\vec b \in B$ , где $B \subseteq B_1 \times B_2 \times \ldots \times B_6$ , ( $j= \overline {1,6}$ ) - множество значений j-го параметра модели злоумышленника, модель криптосистемы - $\vec c \in C$ , где $C \subseteq C_1 \times C_2 \times \ldots \times C_6,$ ( $k= \overline{1,6}$ ) - множество значений k-го параметра модели криптосистемы в соответствии с многокритериальной классификацией. Заметим, что множества значений параметров модели атаки, злоумышленника и криптосистемы конечны.

При дальнейшем изложении для краткости слово "модель" применительно к модели атаки, модели злоумышленника и модели криптосистемы будем опускать.

С каждой атакой будем связывать значение риска, вычисляемое по общеизвестной формуле на основе двух факторов - вероятности происшествия и тяжести возможных последствий:

Риск = Влияние Вероятность

Обозначим через $\Re : A \times B \times C \to [0;1]$ функцию, задающую уровень риска, связанного с атакой $\vec a \in A$ в условиях, когда она может быть применена злоумышленником $\vec b \in B$ для взлома криптосистемы $\vec c \in C$ .

Пусть $I : C \times A \to [0;1]$ - функция влияния (от англ. impact - влияние, воздействие). Под влиянием мы будем понимать степень ущерба от применения атаки $\vec a \in A$ к криптосистеме $\vec c \in C$ .

Пусть $P : B \times A \to [0;1]$ - вероятность того, что злоумышленник $\vec b \in B$ предпримет атаку $\vec a \in A$ , т.е. обладает ресурсами для ее осуществления и сочтет эту атаку целесообразной.

Тогда функция риска $\Re$ выражается следующим образом:

$\Re (\vec a, \vec b,\vec c)=I(\vec c, \vec a) * P(\vec b, \vec a)$

Определим функцию $I(\vec c, \vec a)$ . Для этого рассмотрим семейство функций $I_{gh} : C_g \times A_h \to R_+$ , , , где - множество неотрицательных действительных чисел. Здесь функция $I_{gh}$ задает уровень взаимного влияния параметра криптосистемы и параметра атаки :

· $I_{gh}(c,a)=0$ , если атака со значением параметра $a \in A_h$ не применима к криптосистеме со значением параметра $c \in C_g$ ;

· $0 < I_{gh}(c,a) < 1$ , если значение параметра криптосистемы $c \in C_g$ снижает вероятность успешного применения атаки со значением параметра $a \in A_h$ ;

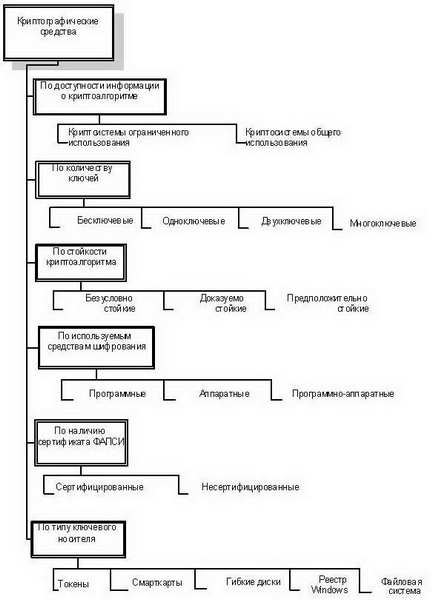
Классификация криптосистем

Рис. 7.3. Классификация криптосистем

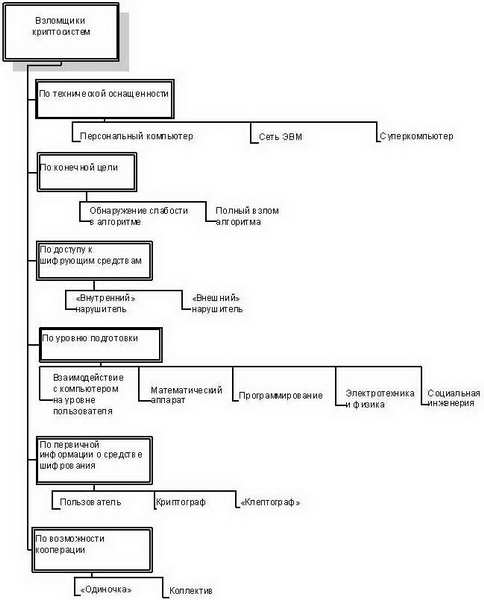
Классификация злоумышленников

Рис. 7.4. Классификация злоумышленников

Классификация криптоатак

увеличить изображение
Рис. 7.5. Классификация криптоатак

· $I_{gh}(c,a)=1$ , если значение параметра криптосистемы $c \in C_g$ не влияет на применимость атаки с параметром $a \in A_h$ ;

· $I_{gh}(c,a) > 1$ , если значение параметра криптосистемы $c \in C_g$ указывает на то, что атака с параметром $a \in A_h$ применима для ее взлома.

Например, если исследуемый алгоритм шифрования реализован в аппаратном обеспечении, это повышает вероятность применения для взлома криптосистемы атак по побочным каналам [7.37] (это вид криптографических атак, использующих информацию, которая может быть получена с устройства шифрования и не является при этом ни открытым текстом, ни шифртекстом). Уровень взаимного влияния параметров криптосистемы и атаки определяется на основе экспертных оценок.

Обозначим через $\overline {I_{gh}} : C_g \times A_h \to [0;1]$ нормированную функцию:

$\overline {I_{gh}}(c,a)=\frac{I_{gh}(c,a)}{\sum_{\xi \in C_g} I_{gh}(\xi, a)}$

Тогда уровень ущерба от применения атаки $\vec a \in A$ к криптосистеме $\vec c \in C$ вычисляется по следующей формуле:

$I(\vec c, \vec a)=\min\limits_{h=\overline {1,9}} \prod \limits_{g=\overlime {1,5}} \overline {I_{gh}}(c_g,a_h)$

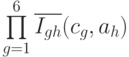где атака и криптосистема заданы параметрами $(a_1,a_2, \ldots , a_9)$ и $(c_1,c_2, \ldots , c_6)$ соответственно. Заметим, что уровень влияния всех параметров криптосистемы на применимость атаки с заданным значением -го параметра в этой формуле вычисляется по мультипликативному критерию: $\prod\limits_{g=1}^6 \overline {I_{gh}} (c_g, a_h)$ . Если значение хотя бы одного из параметров криптосистемы противоречит возможности применения атаки, то результатом оценки применимости атаки к криптосистеме будет нулевое значение, что соответствует нулевому уровню ущерба от атаки.

Функция $P(\vec b, \vec a)$ , определяющая зависимость между параметрами $(a_1,a_2, \ldots , a_9)$ атаки и $(b_1,b_2, \ldots , b_6)$ злоумышленника, выражается аналогично функции $I(\vec c, \vec a)$ . В качестве иллюстрации взаимосвязи параметров злоумышленника и атаки можно привести следующий пример: наличие у предполагаемого взломщика доступа к распределенным вычислительным ресурсам повышает вероятность применения метода "грубой силы" и, вообще говоря, любой атаки, легко поддающейся распараллеливанию.

Таким образом, общая формула для определения уровня риска, связанного с атакой $\vec a \in A$ в условиях, когда эта атака может быть применена злоумышленником $\vec b \in B$ для взлома криптосистемы $\vec c \in C$ , имеет вид:

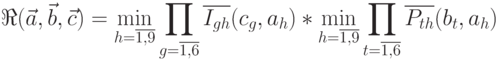
$\Re (\vec a, \vec b, \vec c)=\min\limits_{h=\overline {1,9}} \prod\limits_{g=\overline {1,6}} \overline {I_{gh}} (c_g, a_h) * \min\limits_{h=\overline {1,9}} \prod\limits_{t=\overline {1,6}} \overline {P_{th}} (b_t, a_h)$

Будем считать, что криптосистема $\vec c \in C$ подвержена атаке $\vec a \in A$ в условиях, когда ей угрожает злоумышленник $\vec b \in B$ , если $\Re (\vec a, \vec b, \vec c) > \theta$ , т.е. связанный с ней уровень риска превышает заданное пороговое значение $\theta$ , где $\theta \in [0;1]$ . Допустимый уровень риска $\theta$ является настраиваемым параметром ABC -модели угроз криптосистемы. Значение $\theta$ задается с учетом двух критериев:

· критичности защищаемых данных;

· временных и других ресурсов, доступных специалисту, который осуществляет аудит системы.

В общем случае:

· криптосистема может включать несколько подсистем (например, генератор ключей и симметричный шифратор), к каждой из которых применим свой набор атак;

· на криптосистему может нападать несколько злоумышленников.

Множество атак, которым подвержена криптосистема, состоящая из подсистем $\vec c \in C'$ ( $C' \subseteq C$ ), в условиях, когда ей угрожают злоумышленники $\vec b \in B'$ ( $B' \subseteq B$ ), будем определять по формуле $\Lambda = \cup\limits_{\vec b \in B'} \cup\limits_{\vec c \in C'} \lambda (\vec b, \vec c)$ , где $\lambda (\vec b, \vec c)=\{ \vec a \in A : \Re (\vec a, \vec b, \vec c) > \theta \}$ при заданном уровне риска. Для оценки защищенности криптосистемы необходимо с использованием инструментальных средств оценить ее способность противостоять атакам, входящим в множество $\Lambda$ .

В описанной математической модели сделаны следующие допущения:

· не учитывается зависимость параметров атаки от сочетания параметров криптосистемы, хотя влияние каждого параметра принимается во внимание;

· не учитывается возможность совместных действий со стороны взломщиков различных типов, хотя можно задать модель нападения со стороны однородного коллектива злоумышленников.

Исправление ABC -модели с учетом указанных допущений привело бы к ее значительному усложнению. Вопрос о том, насколько эти допущения снижают точность моделирования угроз безопасности, подлежит дальнейшим исследованиям.

Важно отметить, что разработанная классификационная схема для построения моделей атак на алгоритмы шифрования с небольшими модификациями применима и для моделирования атак на криптопротоколы. Возможность использования ABC -модели угроз для комплексного исследования криптосистемы является важной, т.к. вопрос совместного функционирования криптопротоколов и шифров в рамках одной криптосистемы, как показано в [7.27], до сих пор был мало изучен.

Оценка стойкости криптографических средств к идентифицированным угрозам

После того, как выделен набор атак, представляющих наибольшую угрозу для защищаемых данных, необходимо оценить способность криптосистемы противостоять этим атакам.

Базой для получения таких оценок может служить статистика взлома и успешных атак на криптосистемы. Например, известно, что стартовавший в 1997 г. на сайте www.distributed.net проект "распределенного взлома" RC5-64 (блочного шифра компании RSA, использующего 64-битный ключ) [7.29], в котором на добровольной основе приняли участие более 300 тысяч пользователей глобальной сети, был успешно завершен за пять лет (1757 дней) - за это время было перебрано 85% всего пространства ключей. Однако такая информация, во-первых, не всегда доступна, а, во-вторых, со временем теряет актуальность, т.к. повышение производительности вычислительной техники и появление новых видов атак на шифры ведет к понижению стойкости известных криптографических алгоритмов. Для проверки надежности шифров, используемых в криптосистеме, специалисту необходим набор инструментальных средств, позволяющих осуществлять криптоанализ и не предполагающих у использующего их специалиста наличия глубоких знаний в программировании или электротехнике. В качестве примера можно привести упомянутые в п.1.1 автоматизированные средства анализа криптопротоколов [7.7] или прототип программного комплекса для моделирования атак по побочным каналам [7.37], описанный в [7.19]. Моделирование аппаратного обеспечения в работе [7.19 осуществляется с использованием SystemC [7.2] - языка проектирования и верификации моделей системного уровня, реализованного в виде библиотеки на C++ с открытым исходным кодом. На примере программных и аппаратных реализаций шифра AES показано, каким образом разработанный инструмент позволяет обнаружить уязвимости в реализации криптографического алгоритма.

Особого внимания заслуживают асимметричные криптосистемы. Функциональные возможности шифров с открытым ключом используются в разнообразных технологиях, в числе которых [7.33]:

· Управление идентичностью;

· Цифровая подпись кода;

· Доверенная платформа;

· Управление авторством;

· Построение VPN ;

· Гарантированное уничтожение информации;

· Защита от физической кражи носителя информации.

Процесс криптоанализа асимметричных шифров сопряжен с решением задач из теории чисел и общей алгебры, т.к. практически все используемые алгоритмы асимметричной криптографии основаны проблемах факторизации и дискретного логарифмирования в различных алгебраических структурах. Чтобы определить, могут ли математические задачи той или иной размерности считаться достаточно прочным фундаментом для криптографических целей, специалисту требуются инструментальные средства, позволяющие оценивать быстродействие алгоритмов факторизации и дискретного логарифмирования. Необходимо учитывать, что криптоаналитик может не обладать навыками в области программирования. Кроме того, важно предусмотреть возможность работы под управлением наиболее распространенной ОС - MS Windows.

Итак, выделим набор основных требований к инструментальным средствам криптоанализа:

· Эффективность вычислений с длинными числами в модулярной арифметике;

· Наличие алгоритмов работы с разреженными матрицами;

· Наличие алгоритмов создания факторной базы, решета и разложения на множители;

· Удобство пользовательского интерфейса;

· Возможность сборки в ОС Windows.

Будем считать, что решение соответствует поставленной задаче, если оно удовлетворяет всем перечисленным пяти критериям оценки.

Анализ существующих подходов

Математические пакеты Maple [7.36] и Mathematica [7.45] отличаются простотой кодирования алгоритмов и не имеют встроенных ограничений на разрядность операндов. Тем не менее, помимо платформенной зависимости они обладают критическим недостатком - низкой эффективностью теоретико-числовых операций.

Высокой эффективности можно добиться, используя встроенные средства низкоуровневого языка программирования для разработки функций, необходимых для исследования криптосистем. Однако важно отметить, что реализация примитивов для конструирования современных методов криптоанализа асимметричных шифров оперирует числами в длинной арифметике. Встроенные числовые типы языков C и C++ имеют ограниченную разрядность:

· long: 32 бита;

· long long: 64 бита;

· double: 53 бита - мантисса, 11 бит - экспонента;

· long double: в зависимости от реализации языка может быть определен как double (см. выше) либо как extended double: 64 бита - мантисса, 15 бит - экспонента [7.1].

В реализации языков на платформе . NET отсутствует тип extended double: он доступен только неявно при выполнении промежуточных вычислений (например, где умножение дает результат, выходящий за пределы диапазона значений double, но последующее деление возвращает промежуточный результат обратно в этот диапазон). Кроме того, существует встроенный 128-битный тип данных decimal, позволяющий представлять целые числа разрядностью до 96 бит (в соответствии с размером мантиссы), однако он реализуется в режиме эмуляции, поскольку аппаратная поддержка этого типа на сегодняшний день отсутствует [7.11].

Java поддерживает возможность работы с длинными числами и обладает переносимостью, однако недостатком является низкая эффективность реализации.

Рассмотрим специализированные библиотеки функций для работы с длинной арифметикой и теоретико-числовыми задачами, находящиеся в открытом доступе: LIP, LiDIA, CLN, GMP, NTL.

Библиотека для работы с длинной арифметикой LIP (Long Integer Package) [7.18] является одной из первых таких библиотек. Она была разработана на языке ANSI C известным специалистом Арженом Ленстрой (Arjen K. Lenstra) и поддерживается Полом Лейлендом (Paul Leyland). При хорошей переносимости эта библиотека обладает низкой эффективностью. Кроме того, в ней отсутствует поддержка высокоуровневых теоретико-числовых алгоритмов.

Библиотека CLN (a Class Library for Numbers) [7.8] реализует элементарные арифметические, логические и трансцендентные функции. Авторами библиотеки являются Бруно Хейбл (Bruno Haible) и Ричард Крекел (Richard Kreckel). CLN содержит большой набор классов, реализованных на C++, в частности, классы для поддержки модулярной арифметики, операций с целыми, рациональными и комплексными числами, числами с плавающей запятой. Поскольку числовая библиотека задумывалась как универсальная, это привело к ее ограниченной применимости для решения узкоспециализированных задач.

Библиотека теоретико-числовых алгоритмов LiDIA [7.16], предложенная Томасом Папаниколау (Thomas Papanikolau, Technical University of Darmstadt), написана на C++,поддерживает различные пакеты для работы с целыми числами ( GMP, CLN, LIP ) и характеризуется высокоэффективными реализациями типов данных с увеличенной точностью и алгоритмов с большой временной сложностью. Недостатком библиотеки LiDIA является невозможность сборки в операционных системах Windows, что очень существенно в связи с широким использованием продуктов Microsoft и необходимостью проверки их защищенности.

При разработке GMP ( GNU Multiple Precision arithmetic library ) [7.12] был сделан упор на скорость. Эффективность от использования библиотеки теоретико-числовых алгоритмов GMP растет при увеличении разрядности операндов. Часть функций реализована на языке C, часть - на ассемблере. Автором является Торбжорд Гранланд (Torbjord Granlund). Помимо несовместимости с платформой Windows, недостатком GMP является отсутствие алгоритмов формирования факторной базы, разложения на множители и ряда других, необходимых для реализации современных методов криптоанализа.

Таблица 7.1. Сравнительный анализ программных решений для решения задач криптоанализа
Решение	Mathematica	*LIP*	*CLN*	LiDIA	GMP	NTL	КРИПТО
Критерии оценки	Mathematica	*LIP*	*CLN*	LiDIA	GMP	NTL	КРИПТО
Эффективность вычислений	-	-	-	+	+	+	+
Возможность сборки в ОС Windows	+	+	+	-	-	+	+
Наличие алгоритмов работы с разреженными матрицами	-	-	-	+	+	-	+
Наличие алгоритмов создания факторной базы, решета и разложения на множители	-	-	-	+	-	-	+
Удобство пользовательского интерфейса	+	-	-	-	-	-	+

Известная математическая библиотека библиотека NTL (a Library for doing Number Theory) [7.20] разработана Виктором Шаупом (Victor Shoup) для поддержки теоретико-числовых алгоритмов. Функции, реализованные на языке C++,характеризуются переносимостью. Библиотеку можно использовать совместно с GMP в целях повышения эффективности. NTL имеет большое количество преимуществ по сравнению с рассмотренными аналогами (см. табл. 7.1), однако для решения поставленной задачи реализованных в библиотеке NTL алгоритмов недостаточно. Кроме того, для ее использования в криптоанализе специалист должен обладать квалификацией программиста.

Как видно из табл. 7.1, ни одно из рассмотренных решений не удовлетворяет одновременно всем пяти установленным критериям.

Инструментальные средства криптоанализа асимметричных шифров

Для оценки стойкости криптосистем аналитику необходим инструмент, эффективно работающий с теоретико-числовыми задачами, обладающий простым пользовательским интерфейсом и легко расширяемый. Прототип такого средства для криптоанализа систем с открытым ключом реализован в виде программного комплекса "Инструментальные средства криптоанализа асимметричных шифров" (обозначение в таблице - КРИПТО) [7.31, 7.32]. Программный комплекс состоит из библиотеки КОНСТРУКТОР, включающей необходимые примитивы для конструирования современных методов криптоанализа асимметричных шифров, и приложения АНАЛИТИК, имеющего графический интерфейс пользователя для доступа алгоритмам факторизации и дискретного логарифмирования с использованием функций библиотеки КОНСТРУКТОР. Библиотека КОНСТРУКТОР написана на языке C++ и содержит компоненты, реализующие следующие основные функции:

· Дискретное логарифмирование;

· Факторизация целых чисел;

· Тестирование чисел на простоту;

· Решение систем линейных уравнений в кольцах вычетов и конечных полях.

Для выполнения операций с длинными числами использована библиотека NTL. Выбор базовой библиотеки, обусловленный её функциональностью, скоростью, компактностью (исходный код занимает чуть более 600 килобайт) и переносимостью, позволил получить эффективные реализации перечисленных теоретико-числовых алгоритмов. В настоящей работе мы не будем приводить полное сравнение библиотеки КОНСТРУКТОР с аналогами; заметим лишь, что если на решение задачи дискретного логарифмирования размерностью 55 бит с использованием системы Maple уходит порядка 8 часов, то разработанный программный комплекс КРИПТО позволяет за 10 минут вычислить дискретный логарифм в поле разрядностью 80 бит (испытания проводились на компьютере со следующими аппаратными характеристиками: процессор Intel Pentium IV 3,20GHz, ОЗУ 1Гб).

Расчет эффективности капитальных вложений в использование криптографических средств

Оценки вероятности взлома криптосистемы за определенный период позволяют определить сокращение риска НСД к данным от использования криптосистемы, например, за 1-й год - на 95%, за 2-й год - на 70%, за 3-й год - на 35%. При наличии достоверных оценок объема потерь от реализации угроз нарушения конфиденциальности, целостности или доступности защищаемых данных можно получить математические ожидания потерь и использовать их для определения эффективности криптосистемы с экономических позиций.

Анализ существующих подходов

В настоящее время нет единых стандартов, позволяющих оценить СКЗИ с экономических позиций, поэтому любой из разработанных методов заслуживает отдельного рассмотрения с выявлением его положительных и отрицательных сторон, а также сравнения его с другими представителями этого класса. В табл. 7.2 представлены результаты сравнительного анализа методов оценки эффективности инвестиций в средства обеспечения ИБ. На основании результатов был сделан вывод, что оптимальным является метод дисконтирования денежных потоков [7.42], позволяющий получить наиболее полное представление о целесообразности капитальных вложений, хотя и требующий много времени и усилий на расчет экономических показателей.

Методика дисконтирования денежных потоков при оценке эффективности инвестиций в СКЗИ

Определим денежные потоки, связанные с использованием СКЗИ, за период (где t = 0, 1, 2…. T - периоды, Т - горизонт расчета).

С защищаемой информацией связаны значения дохода от ее использования и ущерба от НСД в течение указанного промежутка времени t. Затраты на приобретение, установку и эксплуатацию СКЗИ могут быть определены очень точно. Пусть результаты оценки способности криптосистемы противостоять атакам показали, что в t-м периоде злоумышленник получит доступ к защищаемой информации с вероятностью . Тогда математическое ожидание дохода , связанного с использованием оцениваемой СКЗИ, вычисляется по формуле:

На основании этих данных о притоках и оттоках денежных средств вычисляются финансово-экономические показатели эффективности инвестиций в криптосистему и делаются выводы о ее соответствии потребностям организации.

Таблица 7.2. Сравнительный анализ методов оценки эффективности инвестиций в средства обеспечения ИБ
Методика оценки	Преимущества	Недостатки
Коэффициент возврата инвестиций	Показатель, понятный финансистам.	Отсутствие достоверных методов расчета в области ИТ. "Статичный" показатель.
Совокупная стоимость владения	Позволяет оценить целесообразность реализации проекта на основании оценки только затрат. Предполагает оценку затрат на различных этапах всего жизненного цикла системы.	Не учитывает качество системы безопасности. "Статичный" показатель. Показатель, специфичный для ИТ.
Дисконтированные показатели эффективности инвестиций	Показатель, понятный финансистам. Учитывает зависимость потока денежных средств от времени. Учитывает все потоки денежных средств, связанные с реализацией проекта.	Сложность расчета.

Краткие итоги

Выполнен анализ существующих методов и средств оценки криптосистем, показаны их недостатки. Описаны этапы комплексного процесса оценки эффективности криптографических средств. Рассмотрены многокритериальные классификации криптосистем, атак и злоумышленников, положенные в основу их параметрических моделей. Описана математическая модель угроз безопасности информационных ресурсов, защищенных с использованием СКЗИ. Проведен сравнительный анализ программных средств, позволяющих решать задачи криптоанализа асимметричных шифров, показаны их преимущества и недостатки. Показаны преимущества и недостатки существующих методов обоснования инвестиций в средства обеспечения ИБ. Выделен набор финансово-экономических показателей для оценки эффективности СКЗИ с экономических позиций. Предложена методика дисконтирования денежных потоков при оценке эффективности инвестиций в СКЗИ.

Скачано с www.znanio.ru

Лекция 5. Экономика информационной безопасности на примере оценки криптосистем

Средства криптографической защиты информации (СКЗИ) представляют собой средства вычислительной техники, осуществляющие криптографическое преобразование информации для обеспечения ее безопасности

Кроме того, использование СКЗИ, обеспечивающих устойчивость к взлому ниже некоторой "фоновой" вероятности, является экономически неоправданным [ 7

RiskWatch от одноименной американской компании [ 7

Рис. 7.2. Процесс оценки эффективности криптографической защиты

Математическая модель угроз безопасности информационных ресурсов

Определим функцию . Для этого рассмотрим семейство функций , , , где - множество неотрицательных действительных чисел

Рис. 7.5. Классификация криптоатак · , если значение параметра криптосистемы не влияет на применимость атаки с параметром ; · , если значение параметра криптосистемы указывает…

В общем случае: · криптосистема может включать несколько подсистем (например, генератор ключей и симметричный шифратор ), к каждой из которых применим свой набор атак ;…

Однако такая информация, во-первых, не всегда доступна, а, во-вторых, со временем теряет актуальность, т

Эффективность вычислений с длинными числами в модулярной арифметике; ·

Наличие алгоритмов создания факторной базы, решета и разложения на множители - - - + - - +

Maple уходит порядка 8 часов, то разработанный программный комплекс

Таблица 7.2. Сравнительный анализ методов оценки эффективности инвестиций в средства обеспечения

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также