Понятие степени.

Определение. Степенью числа а с натуральным показателем n  называется число, записываемое как аⁿ  и определяемое по правилу

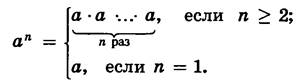
Некоторые степени чисел 2,3,4,5

Определение. Степенью числа а (а ≠ 0) с целым показателем m называется число, записываемое как а^m и определяемое по правилу

Выражения «нуль в нулевой степени» и «нуль в отрицательной степени» не определены.

Если основанием степени является обыкновенная дробь, то удобно использовать правило, которое следует непосредственно из определения:

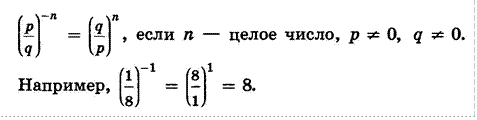
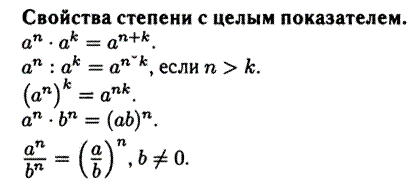
Примеры.

1.  Соотнесите выражения с их значениями

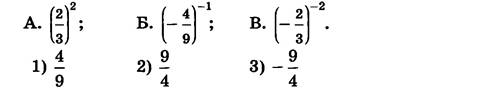
Решение. По определению степени с натуральным показателем 

                                                                                 23 ² = 2 2⋅        = 4.

                                                                                                      3 3     9

По определению степени с целым показателем

^− 94 −1 = 1 =1:− 94  =1⋅− 94 = − 94.

По определению степени с целым показателем

                                                 − 2 ⁻² = −  32 ² = −      32   ⋅ − 32  = 94.

3 

Ответ:  А1,Б3, В2 2. Расположите выражения  5⁻¹;^ ¹5^⁻¹;5 ;⁰ ^ 5¹^² в порядке возрастания их

значений. 

Решение.  Найдем значение каждого числового выражения.

По определению степени с целым показателем:  

По определению степени с целым показателем: 15⁻¹ = 1 =1: 15 =1 5⋅      = 5

По определению степени с целым показателем: 5⁰ = 1.

По определению степени с натуральным показателем:  15² = ^{1 1}5 5⋅ = 251 .

                                                             1        1

         Сравним значения    ,5,1,     заданных числовых выражений: 

                                                             5       25

 1 −2

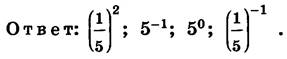
   3. Вычислите:   ₄^_ − 4⁻³ :4⁻⁵ + 2012 .⁰

Решение.  Преобразуем каждое слагаемое, используя свойство степеней. 

 1 −2

   В выражении  4 перейдем к степени с натуральным показателем:

^ 14 ⁻² =  14² = 42.



В выражении 4^-3 · 4^-5 применим свойство деления степеней:

4-3 · 4-5 = 4-3 – (-5) = 42.

По определению степени с целым показателем 2012⁰ = 1.

В итоге получим  14−2 − 4⁻³ :4⁻⁵ + 2012⁰ = 4² − 4² +1.

Ответ: 1.

Квадратные корни

Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а, то есть выполняются условия:

•               a ≥ 0,

2

•               ( a) = a            при любом а ≥ 0.

Свойства арифметического квадратного корня.

1)  Квадратный корень из произведения неотрицательных множителей равен произведению квадратных корней из этих множителей, то есть если           а ≥ 0, b ≥ 0, то ab = a ⋅ b .

2)  Квадратный корень из дроби с неотрицательным числителем и положительным знаменателем равен частному от деления квадратного корня из числителя на квадратный корень из знаменателя, то есть если а ≥ 0, b > 0, то

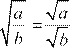
3)  При любом значении а и натуральном k верно равенство

a2k = ak .

Таблица квадратов чисел от 11 до 25

Таблица кубов чисел от 2 до 6

Применение свойств арифметического квадратного корня

          1. Вычислите:    81 0,0001⋅ .

1) ±0,09      2) 0,09       3) 0,03      4) другой ответ

Решение.

1 способ

Подкоренное выражение равно 0,0081. Так как 0,09² = 0,0081, то по определению арифметического квадратного корня 0,0081 = 0,09.

2 способ

          По свойству (1) получим    81 0,0001⋅ =   81⋅   0,0001 = 9 • 0,01 = 0,09. 

Ответ: 2.

2. Вычислите:  .

1) 25      2) ±5       3) 5          4) другой ответ 

Решение.

1 способ

Применим свойство (2). Внесем и число 125, и число 5 под общий корень.

125 125 = = 25 = 5.

                                                                                       5          5

2  способ

В числителе разложим 125 на множители и вынесем множитель из-под знака корня.

              125       25 5⋅     5 5

                          =            =        = 5.

                  5           5          5

Ответ: 3.

3.   Вычислите:  (−3 2)². 

Решение.

Возведем во вторую степень каждый из множителей произведения (−3 2)² = −( 3)² ⋅( 2)² = 9 2⋅        =18. 

Ответ: 18.

4.   Вычислите:  .

1) 2,2       2) ± 2,2        3) 0,44         4) другой ответ 

Решение.

Чтобы вычислить значение арифметического квадратного корня из смешанного числа, переведем смешанное число в неправильную дробь и применим свойство (2):

                   21       4 25⋅ + 21      121      121    11      1

               4     =                   =         =         =     = 2   = 2,2.

                   25            25             25        25      5       5

Ответ: 1.

Если сразу не удается вычислить значение корня, то часто помогает разложение подкоренного выражения на множители.

            5. Найдите значение выражения 12 15 20⋅  ⋅        . 

Решение.

1  способ (непосредственно) 12 15 20⋅ ⋅ = 3600 = 60.

2  способ (с помощью разложения на множители)

              12 15 20⋅  ⋅              = 4 3 3 5 2 10⋅ ⋅ ⋅ ⋅          ⋅          =   4 9 100⋅      ⋅        = 2 3 10⋅ ⋅           = 60. 

Ответ: 60.

Предостережение. При возведении в квадрат произведения возводите в степень все множители. Сокращение дроби выполняйте аккуратно.

Совет. Запишите «квадрат» (и даже куб) умножением двух (трех) скобок, не возводя в степень. Ответ будет без корня. Обязательно сократите дробь.

6.               ^{5 12⋅}          ₌ ⁶⁰ ₌ 3.                                                          Ответ: 3.

                         20           20

7.               Найдите значение выражения ^{(3 5)2}

15

 .                               Ответ: 3.

8.               2 2 5 3⋅   ⋅        6 = 2 5⋅      ⋅        2 3 6⋅ ⋅        =10⋅  36 =10 6⋅    = 60 .       Ответ: 60.

9.                .                                                                 Ответ:  .

10.          3⁶ ⋅2⁴ ⋅5² =        3⁶ ⋅     2⁴ ⋅     5² = ( 3 )^{3 2} ⋅( 2 )^{2 2} ⋅         5² =

               = 3 2 5 27 4 5 540³ ⋅ ² ⋅                                   =     ⋅        ⋅        =       .                                                  Ответ: 540.

11.          Найдите значение выражения: ^{(5 3)2} .

15

 .                                                      Ответ: 5.