Добавить материал

и получить 10 документов
и свидетельство СМИ

Изображение пользователя Шкода Лидия Ильинична Шкода Лидия Ильинична

Логарифмические уравнения из материалов ЕГЭ базового уровня.

  • Домашняя работа
  • docx
  • 09.03.2023
Публикация в СМИ для учителей

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал
Работа содержит 10 разобранных заданий с подробным решением и 11 заданий для самостоятельного решения.
Иконка файла материала Лог.ур.базов.из ЕГЭ.docx

Логарифмические уравнения из материалов ЕГЭ базового  уровня.

 (Для всех уравнений делается проверка или находится ОДЗ).

1. Найдите корень уравнения \log _\tfrac17 левая круглая скобка 7 минус x правая круглая скобка = минус 2.

Решение. Последовательно получаем:

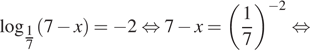
\log _\tfrac17 левая круглая скобка 7 минус x правая круглая скобка = минус 2 равносильно 7 минус x= левая круглая скобка дробь: числитель: 1, знаменатель: 7 конец дроби правая круглая скобка в степени левая круглая скобка минус 2 правая круглая скобка равносильно
равносильно 7 минус x=49 равносильно x= минус 42.

 Ответ: −42.

2. Найдите корень уравнения \log _5} левая круглая скобка 5 минус x правая круглая скобка =\log _53.

Решение. Последовательно получаем:

\log _5 левая круглая скобка 5 минус x правая круглая скобка =\log _53 равносильно 5 минус x=3 равносильно x=2.

 Ответ: 2.

3. Решите уравнение логарифм по основанию 5 левая круглая скобка x в квадрате плюс 2x правая круглая скобка = логарифм по основанию 5 левая круглая скобка x в квадрате плюс 10 правая круглая скобка .

Решение. Перейдем к одному основанию степени:

\log _5 левая круглая скобка x в квадрате плюс 2x правая круглая скобка =\log _5 левая круглая скобка x в квадрате плюс 10 правая круглая скобка равносильно x в квадрате плюс 2x=x в квадрате плюс 10 равносильно x=5.Ответ: 5.

4. Найдите корень уравнения \log _5 левая круглая скобка 5 минус x правая круглая скобка =2\log _53.

Решение. Последовательно получаем:

\log _5 левая круглая скобка 5 минус x правая круглая скобка =2\log _53 равносильно 5 минус x=3 в квадрате равносильно 5 минус x=9 равносильно x= минус 4.

Ответ: −4.

5. Решите уравнение логарифм по основанию 5 левая круглая скобка 7 минус x правая круглая скобка = логарифм по основанию 5 левая круглая скобка 3 минус x правая круглая скобка плюс 1.

Решение. Заметим, что 1= логарифм по основанию левая круглая скобка 5 правая круглая скобка 5и используем формулу логарифм по основанию a b плюс логарифм по основанию a c= логарифм по основанию левая круглая скобка a правая круглая скобка bc.Имеем:

\log _5 левая круглая скобка 7 минус x правая круглая скобка =\log _5 левая круглая скобка 3 минус x правая круглая скобка плюс 1 равносильно
равносильно логарифм по основанию 5 левая круглая скобка 7 минус x правая круглая скобка = логарифм по основанию 5 левая круглая скобка 3 минус x правая круглая скобка плюс логарифм по основанию 5 5 равносильно

 

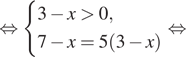
равносильно система выражений новая строка 3 минус x больше 0, новая строка 7 минус x=5 левая круглая скобка 3 минус x правая круглая скобка конец системы . равносильно
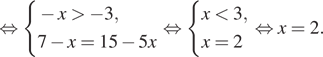
равносильно система выражений новая строка минус x больше минус 3, новая строка 7 минус x=15 минус 5x конец системы . равносильно система выражений новая строка x меньше 3, новая строка x=2 конец системы . равносильно x=2.

 Ответ: 2.

6. Решите уравнение логарифм по основанию левая круглая скобка x минус 5 правая круглая скобка 49=2.Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Решение. На ОДЗ перейдем к уравнению на основание логарифма: \log _x минус 549=2 равносильно система выражений новая строка левая круглая скобка x минус 5 правая круглая скобка в квадрате =49, новая строка x минус 5 больше 0, новая строка x минус 5 не равно 1 конец системы . равносильно


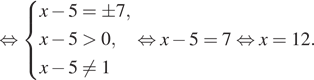
равносильно система выражений новая строка x минус 5=\pm 7, новая строка x минус 5 больше 0, новая строка x минус 5 не равно 1 конец системы . равносильно x минус 5=7 равносильно x=12.

Итак, на ОДЗ уравнение имеет только один корень.

 Другое решение.

\log _x минус 5}49=2 равносильно \log _x минус 5}7 в квадрате =2 равносильно 2\log _x минус 5}7=2 равносильно \log _x минус 5}7=1 равносильно x минус 5=7 равносильно x=12.

 Ответ: 12.

7. Найдите корень уравнения логарифм по основанию левая круглая скобка 8 правая круглая скобка 2 в степени левая круглая скобка 8x минус 4 правая круглая скобка = 4.

Решение. Используем формулу логарифм по основанию левая круглая скобка a в степени m правая круглая скобка a в степени n = дробь: числитель: n, знаменатель: m конец дроби :

логарифм по основанию левая круглая скобка 8 правая круглая скобка 2 в степени левая круглая скобка 8x минус 4 правая круглая скобка =4 равносильно логарифм по основанию левая круглая скобка 2 в кубе правая круглая скобка 2 в степени левая круглая скобка 8x минус 4 правая круглая скобка =4 равносильно
равносильно дробь: числитель: 8x минус 4, знаменатель: 3 конец дроби =4 равносильно 8x минус 4=12 равносильно x=2.

Приведем другое решение:

логарифм по основанию левая круглая скобка 8 правая круглая скобка 2 в степени левая круглая скобка 8x минус 4 правая круглая скобка =4 равносильно 2 в степени левая круглая скобка 8x минус 4 правая круглая скобка =8 в степени 4 равносильно
равносильно 2 в степени левая круглая скобка 8x минус 4 правая круглая скобка =2 в степени левая круглая скобка 12 правая круглая скобка равносильно 8x минус 4=12 равносильно x=2.

 Ответ:2.

8. Найдите корень уравнения 2 в степени левая круглая скобка логарифм по основанию левая круглая скобка 8 правая круглая скобка левая круглая скобка 5x минус 3 правая круглая скобка правая круглая скобка = 4.

Решение. Используя формулу a в степени левая круглая скобка логарифм по основанию b c правая круглая скобка =c в степени левая круглая скобка логарифм по основанию b a правая круглая скобка ,получаем:

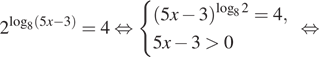
2 в степени левая круглая скобка логарифм по основанию левая круглая скобка 8 правая круглая скобка левая круглая скобка 5x минус 3 правая круглая скобка правая круглая скобка = 4 равносильно система выражений левая круглая скобка 5x минус 3 правая круглая скобка в степени левая круглая скобка логарифм по основанию левая круглая скобка 8 правая круглая скобка 2 правая круглая скобка = 4,5x минус 3 больше 0 конец системы равносильно
равносильно левая круглая скобка 5x минус 3 правая круглая скобка в степени д робь: числитель: 1, знаменатель: 3 конец дроби =4 равносильно 5x минус 3 = 64 равносильно x =13,4.Ответ: 13,4.

 Примечание.   Следует отличать это уравнение от похожего, но другого: 2 в степени левая круглая скобка логарифм по основанию левая круглая скобка 8 правая круглая скобка 5x минус 3 правая круглая скобка = 4.В этом случае имеем:

2 в степени левая круглая скобка логарифм по основанию левая круглая скобка 8 правая круглая скобка 5x минус 3 правая круглая скобка =4 равносильно 2 в степени левая круглая скобка логарифм по основанию левая круглая скобка 8 правая круглая скобка 5x минус 3 правая круглая скобка =2 в квадрате равносильно логарифм по основанию левая круглая скобка 8 правая круглая скобка 5x минус 3 =2 равносильно
равносильно логарифм по основанию левая круглая скобка 8 правая круглая скобка 5x =5 равносильно 5x=8 в степени 5 равносильно x= 6553,6.

9. Решите уравнение логарифм по основанию x 32=5..

Решение. На ОДЗ перейдем к уравнению на основание логарифма:

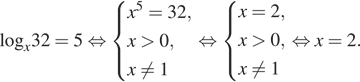
\log _x32=5 равносильно система выражений новая строка x в степени 5 =32, новая строка x больше 0, новая строка x не равно 1 конец системы . равносильно система выражений новая строка x=2, новая строка x больше 0, новая строка x не равно 1 конец системы . равносильно x=2.

Итак, на ОДЗ уравнение имеет только один корень.

 

Ответ: 2.

10. Решите уравнение   ln log2 log3 4x =0   Решение.      ln b = loge b      Основание  натурального логарифма ln равно числу е, поэтому по определению логарифма, запишем:  е0 = 1. Значит  log2 log3 4x =1 log3 4x = 21   log3 4x = 21        4х =32     х=2,25    Ответ: 2,25.

 

Решить самостоятельно.

 

 

1.    Найдите корень уравнения       логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка 4 минус x правая круглая скобка =7.

 

2.    Найдите корень уравнения      \log }_2} левая круглая скобка 15 плюс x правая круглая скобка =\log _23.

 

3.    Найдите корень уравнения      \log _4 левая круглая скобка x плюс 3 правая круглая скобка =\log _4 левая круглая скобка 4x минус 15 правая круглая скобка .

 

4.    Найдите корень уравнения     log 6 (12x +10) = 2 log 6 7

 

5.    Найдите корень уравнения     log 2 (x2 -4x) =  log 2 (6x – 16)

 

6.    Найдите корень уравнения       log 3 (21 -x) =  log 3 (x-7) +2

 

7.    Найдите корень уравнения       log 9 – 4x 144 = 2

 

8.    Найдите корень уравнения        lg 100 4x -2   = 4

 

9.    Найдите корень уравнения       3 log 9 (2x + 6) = 9

 

10.Найдите корень уравнения       log x 81 = 4 

 

11. Найдите корень уравнения       log 1,5 log 5 log 2 8x = 0

 

 

 

 

 

 

 

 

 

 

Ответы на задания.

1.      -124

 

2.       -12

 

3.         6

 

4.       55,75

 

5.          8

 

6.       8,4

 

7.      -0,75

 

8.          1

 

9.        37,5

 

10.         3

 

11.         4

 

Логарифмические уравнения из материалов Итак, на ОДЗ уравнение имеет только один корень Решить самостоятельно. 1 Ответы на задания. 1. -124 2

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также