Мастер-класс "Активизация познавательной деятельности учащихся в процессе обучения математики»

Мастер-класс

"Активизация познавательной деятельности учащихся в процессе обучения математики»

Учитель математики Рябова Т.А.

МБОУ «Садовская СШ»

Цель “Мастер-класса”: показать методические приемы активизации познавательной активности учащихся на уроках математики.

Учение, лишённое всякого интереса и взятое только силой принуждения, убивает в ученике охоту к овладению знаниями. Приохотить ребёнка к учению гораздо более достойная задача, чем приневолить.

К.Д. Ушинский

Ход занятия

Добрый день, уважаемые коллеги. Нам с вами сегодня предстоит выполнить совместно большую работу. Тема нашего занятия мастер – класса «Активизация познавательной активности учащихся в процессе обучения математики». Это очень сложный вопрос и нам предстоит докопаться до истины. Каждого из вас, в том числе и меня, интересует ответ на вопрос «Каким мы хотим видеть ученика на уроке?»……..

Особое  внимание  уделяю  организации  начала  урока.  Удачно  выбранный  вид деятельности  в  начале  урока  настраивает  на  плодотворную  работу.  Творческие,  причем посильные  задания  наиболее  цепко  держат  внимание  ребят,  включают  их  в  урок, обеспечивают  положительную  мотивацию.  Данное  занятие предлагаю  провести  в  форме экскурсии.

Решить анаграмму

(в словах изменен порядок букв). Какое слово зашифровано?

ренунеави

Оформление доски.

Эмблема 28k + 30n + 31m = 365

Комментарий учителя к уравнению:

Говорят,  уравнение вызывает сомнение, но итогом сомнения может быть озарение!

Задание. Найти хотя бы одно решение уравнения. К его решению вернёмся в конце занятия.

А теперь совершим экскурсию в математику!

План экскурсии.

1. Развиваем гибкость ума через решение задач.

2. Ситуации в жизни такие: либо сложные, либо простые.

3. Без логики нет математики.

4. В геометрию тропинки одолеем без запинки.

5. Точка соприкосновения: “Где же зарыта кошка?”

Ход занятия

 Организационный момент. Посмотрим друг на друга и улыбнёмся друг другу. Можно необычно начать урок поздороваться локтями. Эта смешная игра позволяет весело начать урок, размяться перед более серьезными упражнениями, способствует контакту между учениками. ( Метод «Поздоровайся локтями»)

Пригласительныйбилет

Пригласительный билет

Экскурсия будет проводить по группам. 

I этап. Развиваем гибкость ума через решение задач.

На  примере  этого  типа  заданий  учу  применять  переформулировки  условия задачи или переключаться с прямого хода мыслей на обратный.

1) У двух зрячих один брат слепой, но у слепого нет зрячих братьев. Как это может быть? (из первой фразы как будто следует, что речь в задаче идет о братьях, тогда как на самом деле зрячими оказываются сестры).

2) Дано 5 спичек. Сложите их них 2 равносторонних треугольника. А теперь сложите из 6 спичек  –  4  равносторонних  треугольника  (первая  задача  решается  в плоскости,  а  вторая  в пространстве).

На  примере  этого  типа  заданий  отрабатываю  навыки  расширения  сферы поиска  решения,  учу  отделять  главное  от  второстепенного,  извлекать  из  текста  не только то, что там сказано прямо, но и то, что содержится между строк.

1)  Известно,  что  бумеранг  можно  бросить  так,  что  он  вернется  обратно.  А  можно  как-то ухитриться и бросить теннисный мяч так, чтобы он вернулся обратно? 

Ответ: мяч нужно бросить вверх и он вернется обратно.

IIэтап. Ситуации в жизни такие: либо сложные, либо простые.

 На примере этого типа заданий учу видеть главные причины происходящего, объяснять  их  сущность,  делать  выводы,  находить  закономерности,  отрабатывать вычислительные навыки.

Решить задачу: Найди закономерность и продолжи ряд.

29,18,24,13,19…(8)

16,64,256…(1024)

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

По коэффициентам  p и  q приведенного квадратного уравнения можно предсказать знаки корней.

Решите уравнения используя свойства коэффициентов.

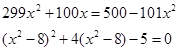 Слайд№11

Для работы над темой урока можно использовать методы «Ульи», «Визитные карточки», «Экспертиза», «Карта группового сознания». Для проведения дискуссии и принятия решений – методы «Cветофор», «Приоритеты», «На линии огня». Для представления материала самостоятельной работы обучающихся – «Инфо-карусель», «Автобусная остановка», «Ярмарка».

Пример АМ организации самостоятельной работы над темой

Метод «Автобусная остановка»

Цель: научиться обсуждать и анализировать заданную тему в малых группах.
Группы: 5-7 человек
Численность: весь класс
Время: 20-25 мин.
Материал: листы большого формата (ватман, плакат, блокнот для флипчата), фломастеры.

Проведение:
Учитель определяет количество обсуждаемых вопросов новой темы (оптимально 4-5). Участники разбиваются на группы по числу вопросов (5-7 человек в каждой).

Группы распределяются по автобусным остановкам. На каждой остановке (на стене или на столе) расположен лист большого формата с записанным на нем вопросом по теме. Учитель ставит задачу группам – записать на листе основные моменты новой темы, относящиеся к вопросу. В течение 5 минут в группах обсуждаются поставленные вопросы и записываются ключевые моменты. Затем по команде учителя группы переходят по часовой стрелке к следующей автобусной остановке. Знакомятся с имеющимися записями и, при необходимости, дополняют их в течение 3 минут. Исправлять существующие записи, сделанные предыдущей группой нельзя. Затем следующий переход к новой автобусной остановке и еще 3 минуты на знакомство, обсуждение и добавление своих записей. Когда группа возвращается к своей первой остановке, она в течение 3 минут знакомится со всеми записями и определяет участника группы, который будет представлять материал. После этого каждая группа презентует результаты работы по своему вопросу. В завершении учитель резюмирует сказанное всеми группами, при необходимости вносит коррективы и подводит итоги работы.

Примечание: Желательно организовать автобусные остановки (прикрепить листы с вопросами) в разных углах учебной комнаты, чтобы в процессе обсуждения группы не мешали друг другу. Вопросы изучаемой темы можно стилизовать под названия автобусных остановок.

1Автобусная остановка: основные тригонометрические формулы.

2Автобусная остановка: вид тригонометрической функции и её график.

3Автобусная остановка: тригонометрические уравнения и формулы решения.

4Автобусная остановка: тригонометрические неравенства и их решение.

.

 Активные методы релаксации

Цель – повысить уровень энергии в классе
Если вы чувствуете, что обучающиеся устали, а впереди еще много работы или сложная задача, сделайте паузу, вспомните о восстанавливающей силе релаксации! Иногда достаточно 5 – 10 минут веселой и активной игры для того, чтобы встряхнуться, весело и активно расслабиться, восстановить энергию. Активные методы «Энергия - 1», «Роботы», Постройся по росту», «Красная Шапочка и Серый Волк», «Шест», и многие другие позволят вам это сделать, не выходя из класса.

Пример Активных методов релаксации

Метод «Земля, воздух, огонь и вода»

Численность – весь класс.
Время – 8-10 минут

Проведение:
Учитель просит обучающихся по его команде изобразить одно из состояний – воздух, землю, огонь и воду.

Воздух. Ученики начинает дышать глубже, чем обычно. Они встают и делают глубокий вдох, а затем выдох. Каждый представляет, что его тело, словно большая губка, жадно впитывает кислород из воздуха. Все стараются услышать, как воздух входит в нос, почувствовать, как он наполняет грудь и плечи, руки до самых кончиков пальцев; как воздух струится в области головы, в лицо; воздух заполняет живот, область таза, бедра, колени и стремится дальше – к лодыжкам, ступням и кончикам пальцев.

Ученики делают несколько глубоких вдохов и выдохов. Можно предложить всем пару раз зевнуть. Сначала это получается скорее искусственно, но иногда после этого возникает настоящий зевок. Зевота – естественный способ компенсировать недостаток кислорода. (Зевание может использоваться и по-другому: вы можете на первой встрече предложить зевать сознательно, чтобы группа быстрее «взбодрилась»).

Земля. Теперь ученики должны установить контакт с землей, «заземлиться» и почувствовать уверенность. Учитель вместе с обучающимися начинает сильно давить на пол, стоя на одном месте, можно топать ногами и даже пару раз подпрыгнуть верх. Можно потереть ногами пол, покрутиться на месте. Цель – по-новому ощутить свои ноги, которые находятся дальше всего от центра сознания, и благодаря этому телесному ощущению почувствовать большую стабильность и уверенность.

Огонь. Ученики активно двигают руками, ногами, телом, изображая языки пламени. Учитель предлагает всем ощутить энергию и тепло в своем теле, когда они двигаются подобным образом.

Вода. Эта часть упражнения составляет контраст с предыдущей. Ученики просто представляют себе, что комната превращается в бассейн, и делают мягкие, свободные движения в «воде», следя за тем, чтобы двигались суставы – кисти рук, локти, плечи, бедра, колени.

Можно дать дайте дополнительные 3 минуты времени, чтобы каждый мог создать свою индивидуальную комбинацию элементов.

Примечание: Если учитель сам принимает участие в этом упражнении, помимо пользы для себя, он поможет также и неуверенным и стеснительным ученикам активнее участвовать в упражнении.

IIIэтап. Без логики нет математики.
В процессе урока учителю регулярно приходится сообщать новый материал обучающимся. Такие методы, как «Инфо-угадайка»,  «Кластер», «Мозговой штурм» позволят вам сориентировать обучающихся в теме, представить им основные направления движения для дальнейшей самостоятельной работы с новым материалом.

Пример АМ презентации учебного материала

Вместо привычного устного рассказа учителя о новой теме можно использовать следующий метод представления нового материала:

Метод «Инфо-угадайка»

Цели метода: представление нового материала, структурирование материала, оживление внимания обучающихся.
Группы: все участники.
Время: Зависит от объема нового материала и структуры урока.
Материал: подготовленный лист ватмана, цветные маркеры.

Проведение:
Учитель называет тему своего сообщения. На стене прикреплен лист ватмана или блокнот флипчата, в его центре указано название темы. Остальное пространство листа разделено на секторы, пронумерованные, но пока не заполненные. Начиная с сектора 1, учитель вписывает в сектор название раздела темы, о котором он сейчас начнет говорить в ходе сообщения. Обучающимся предлагается обдумать, о каких аспектах темы, возможно, далее пойдет речь в докладе. Затем учитель раскрывает тему, а в сектор вписываются наиболее существенные моменты первого раздела (можно записывать темы и ключевые моменты маркерами разных цветов). Они вносятся на плакат по ходу сообщения. Закончив изложение материала по первому разделу темы, учитель вписывает во второй сектор название второго раздела темы, и так далее.

Этот метод изложения материала помогает обучающимся следить за аргументацией учителя и видеть актуальный в данный момент рассказа аспект темы. Отчетливое разделение общего потока информации способствует лучшему восприятию. "Белые пятна" стимулируют - многие участники начнут обдумывать, какими будут следующие, пока не обозначенные разделы темы.

На примере логических заданий отрабатываю навыки размышления над задачей, учу отделять главное от второстепенного, вычленять ведущие закономерности явлений.

Такие задачи носят занимательный характер, решение которых развивает логическое мышление  и  не  требуют  большого  запаса  математических  знаний,  поэтому  они привлекают даже тех учащихся, которые не очень любят математику.

Три курицы за три дня несут три яйца. Сколько яиц снесут 12 таких же курей за 12 дней?

Одна курица несет одно яйцо за три дня. За 12 дней одна курица снесет четыре яйца, следовательно, 12 курей за 12 дней снесут 12х4=48 яиц.

 Чтобы люди могли попасть в канализационные коллек­торы или добраться до других подземных коммуника­ций, используются люки. В подавляющем большинстве случаев крышки люков имеют круглую форму, а не квадратную или прямоугольную. Почему?

Крышка квадратного или прямоугольного люка может провалиться в люк, так как длина диагонали люка больше длины стороны крышки. Крышка же круглого люка провалиться не может, как ее ни поверни. Поэтому круглые люки удобнее и безопаснее квадратных.

IV этап. В геометрию тропинки одолеем без запинки. 

1).Найдитеплощадьпрямоугольника, длинысторонкоторогочисленноравныкорнямуравнения√2x² - 17x + 3 = 0.

1) 3√2;        2) 1,5√2 ;          3)  3 ;      4) 8,5√2;      5) 17√2.

Решение. Площадьпрямоугольникаравнапроизведениюдлинегососеднихсторон. Поусловиюдлинысторонданногопрямоугольникачисленноравныкорнямданногоуравнения. Значит, применивтеоремуВиета, покоторойпроизведениекорнейквадратногоуравнения

ax² + bx + c = 0равноc/a, получим:

Sпрямоугольника = 1,5√2, тоестьвернымявляетсявторойвариантответа .Аименно: 1,5√2 .

Слайд№23 решение квадратного уравнения с помощью окружности.

Слайд№24 нахождение периметра параллелограмма.

V этап. Точка соприкосновения: “Где же зарыта кошка?”

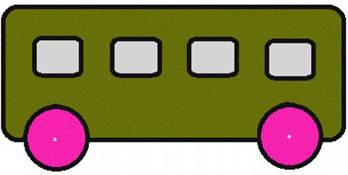
№1Издевательски простая задача, понятная детям и непонятная взрослым. Куда едет автобус?

Ответ

Обычно взрослые, видя схематичное изображение, мигом забывают о деталях. К примеру,  дети часто ездят в школу на автобусе, поэтому знают, с какой стороны у него двери и как он подъезжает. Они понимают, что на картинке не хватает дверей. Значит, автобус едет влево.

№2 Дошкольники решают эту задачу за 5-10 минут. У некоторых программистов уходит на неё до часа. 

Но многие люди, исписав несколько листов бумаги, сдаются.

Ответ

Маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В "9" один кружочек, в "8" — два, в "1" — ни одного, а, значит, 2581 = 2.

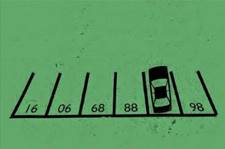
№3 На решение этой задачи у шестилетнего ребенка уходит обычно не больше 20 секунд. А вот неподготовленных взрослых она часто вводит в ступор.

Так какое же число скрыто под машиной?

Ответ

Как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путем. Например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест.

В действительности же, картинку надо просто перевернуть.

№4

• Гений находит решение за 10 секунд.
• Билл Гейтс — за 20 секунд.
• Выпускник Гарварда — за 40 секунд.
• Если вы нашли ответ за 2 минуты, то вы принадлежите к 15% наиболее одаренных людей.
• 75% людей не способны решить эту задачу.

Ответ

Фигура № 1

Пояснение: Сначала вам кажется, что это фигура, у которой нет какого-то общего со всеми признака. Но тут происходит самое интересное:
— Да, № 2 без белой рамки.
— Но как же тогда № 3 — единственный круг?
— № 4 — зеленый, когда остальные красные.
— № 5 явно меньше остальных...
Логика загадки в том, что только № 1 не содержит явных отличий от большинства. И в этом его главное отличие. Поздравляем тех, кто нашел ответ. Не дайте вашим способностям пропасть зря.

Такие  нестандартные  задачи  у  учащихся  вызывают  большой  интерес. 

 Итог занятия.
Для завершения образовательного мероприятия можно использовать такие активные методы как: "Мухомор", «Мудрый совет», «Письмо самому себе», «Все у меня в руках!», «Итоговый круг», «Что я почти забыл?», «Ресторан», «Комплименты». Эти методы помогут вам эффективно, грамотно и интересно подвести итоги урока и завершить работу.

Пример Активных методов подведения итогов урока

Метод «Ресторан»

Цель: Выяснить получить обратную связь от учеников от прошедшего урока.
Время: 5 мин. на подготовку; 1-3 мин. каждому участнику (на ответ).
Численность: Все ученики
Материал: лист большого формата, фломастеры, скотч, цветные карточки

Проведение:
Учитель предлагает ученикам представить, что сегодняшний день они провели в ресторане и теперь директор ресторана просит их ответить на несколько вопросов:
- Я съел бы еще этого…
- Больше всего мне понравилось…
- Я почти переварил…
- Я переел…
- Пожалуйста, добавьте…
Участники пишут свои ответы на карточки и приклеивают на лист флип-чарта, комментируя.

Примечание: Для учителя этот этап очень важен, поскольку позволяет выяснить, что ребята усвоили хорошо, а на что необходимо обратить внимание на следующем уроке. Кроме того, обратная связь от учеников позволяет учителю скорректировать урок на будущее.

Вернемся к эмблеме занятия.

28k + 30n + 31m = 365

Слова учителя: Кто увидел? Кто догадался? Кто решил?

“Смотреть – не значит видеть!”

Ответ: 365 – это количество дней в году, 28 – количество дней в феврале, 30 – количество дней имеют 4 месяца в году, 31 – количество дней имеют 7 месяцев в году. Тогда:

 28 ·1 + 30 · 4 + 31 · 7 = 365.

Вывод.  В применяемой технологии системы эффективных уроков,  важная роль отводится высокопроизводительному уроку, на котором главное: 

·       создание и поддержание высокого уровня познавательного интереса; 

·       экономное расходование времени урока;

·       тренинг умственных действий;

·       объем и прочность полученных знаний;

·       положительный уровень межличностных отношений.

Подобранные  задания  выполняют  познавательные  и воспитательные  функции.  Ученики применяют  приобретенные  знания,  открывают  новые  приемы  и  способы  решений, рассуждений; развивается логическое мышление, развивается смысловая и образная память, формируется  умение  работать  с  нестандартными  задачами,  обязательность  четкого, правильного и наиболее полного объяснения решения той или иной задачи, также является положительной  чертой.  Учащиеся  преображаются  на  глазах,  с  огромным  удовольствием показывают  свои  умения  и  навыки. 

Согласно Концепции модернизации образования и новым ФГОС базовым звеном образования является общеобразовательная школа, модернизация которой предполагает ориентацию образования не только на усвоение обучающимся определенной суммы знаний, но и на развитие его личности, его познавательных и созидательных способностей. Общеобразовательная школа должна формировать целостную систему универсальных знаний, умений, навыков, а также опыт самостоятельной деятельности и личной ответственности обучающихся, то есть ключевые компетенции, определяющие современное качество содержания образования. 

Выпускник школы должен уметь применять полученные в школе знания и умения в реальных жизненных ситуациях.

После выступления представителей всех групп докладчик подводит итог. Как сказал Бернард Шоу: «Един­ственный путь, ведущий к знаниям, — это деятельность». Можно бесконечно долго говорить о том, как провести мастер-класс, но это будут только слова, пока не будет самостоятельно подготовлен и проведен свой первый мастер-класс.

Сегодня вы получили порцию вдохновения — теперь работайте! Ведь и эпиграф семинара: «Правильный путь такой: усвой то, что сделали твои предшественники, и иди дальше».

Спасибо за внимание и активное участие!

В заключение хочу дать несколько советов:

-будьте терпеливы; не ждите быстрых результатов от детей, они обязательно будут, только не торопите события;

-не забывайте о доброжелательности;

- не бойтесь движения и шума на занятиях; практикуйте небольшие физические разминки на уроке, которые снимают интеллектуальную и эмоциональную напряжённость;

-помните о том, что каждый ребёнок имеет право на творческое самовыражение, поэтому не нужно делить детей на талантливых и остальных;

-творите сами; и как нет детей без воображения, так нет и педагога без творческих порывов.

Урок – презентация

Тема урока «Квадратные уравнения (методы решения)» (2ч.)

Цели урока:

1.     Обучающие:

§         обобщение и систематизация знаний по теме;

§         ликвидация пробелов в знаниях учащихся;

§         установление внутри предметных связей изученной темы с другими темами курса алгебры.

2.     Развивающие:

§         расширение кругозора учащихся;

§         пополнение словарного запаса;

§         развитие мышления, внимания, умения учиться.

3.     Воспитание общей культуры.

Оборудование: ПК, проектор, экран;

у каждого ученика: конспект, пригласительный билет, исторический “путеводитель”.

Ход урока:

                              I.           Организационный момент

 Приветствие учащихся; проверка готовности к уроку.

Сообщение темы урока: “Квадратные уравнения (методы решения)”.

Совместное формулирование цели урока.

— Сегодня у нас несколько необычный урок: урок-презентация методов решения квадратных уравнений. Как вы думаете, как можно сформулировать цель нашего урока исходя из его темы? /Речь идет о методах, значит их много (больше одного), надо каждый вспомнить и проиллюстрировать примером./

 Иными словами, обобщить и систематизировать весь предшествующий опыт решения квадратных уравнений. А зачем нам это надо? /Для возможности выбора рационального пути решения./

 Итак, наша цель: обобщить опыт решения квадратных уравнений, научиться выбирать рациональный путь решения.

                           II.           Актуализация знаний

Прежде всего, вспомним, какие уравнения называются квадратными. /Уравнение вида , где х- переменная, a,b,c – числа , называется квадратным./ Квадратное уравнение, записанное в таком виде, является стандартным видом уравнения. Как называются числа a, b, c ?

/ а – старший коэффициент, b – второй коэффициент, с – свободный член/

Вспомним, как традиционно решаются квадратные уравнения разных видов.Первый вид квадратных уравнений – неполные квадратные уравнения. С этим видом квадратных уравнений мы познакомились на первых уроках изучения квадратных уравнений. Вспомним, какие виды неполных квадратных уравнений бывают и как они решаются (анализ таблицы).

Вспомним, как традиционно решаются квадратные уравнения, записанные в стандартном виде. Прежде всего, обратимся к понятию дискриминанта. Для чего и зачем он нужен? Вспомните слово “дискриминация”, что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к разным людям. Оба слова (и дискриминант, и дискриминация) происходят от одного латинского слова, означающего “различающий”. Дискриминант различает квадратные уравнения по числу корней (анализ слайда). Важное дополнение: в таких случаях (D<0) обычно уточняют – нет действительных корней. Дело в том, что в математике, кроме действительных чисел, рассматриваются так называемые мнимые числа; так вот, мнимые корни у такого уравнения есть. О мнимых числах и разрешимости таких квадратных уравнений мы поговорим в старших классах. Мы вспомнили всю “азбуку” квадратного уравнения?

/Нет. Мы не вспомнили теорему Виета./

Формулируем, обращая внимание на условие D0.

Итак, все необходимые, азбучные методы решения повторили, и я приглашаю вас на презентацию иных методов решения квадратных уравнений. И для начала заполним пригласительный билет, лежащий у каждого из вас на столе.

(Подписывают и заполняют таблицу)

Проверим. Возьмите в руки простой карандаш, сверим ответы.

Поднимите руки те, кто безошибочно справились с работой. Молодцы! Передайте свои заполненные билеты вперед.

III.            Презентация специальных методов

Обратимся к конспекту урока. Помимо традиционных методов решения квадратных уравнений есть еще специальные и общие методы. Рассмотрим каждый из специальных методов в отдельности. И оценим его “перспективы”.

Метод выделения квадрата двучлена

Цель: привести уравнение общего вида к неполному квадратному уравнению.

В этом нам помогут формулы сокращенного умножения, а именно, квадратов суммы и разности: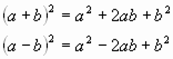 

Решим уравнение х²-6х+8=0 методом выделения квадрата двучлена.

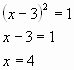,или 

Ответ: 2;4.

Замечание: метод применим для любых квадратных уравнений, но не всегда удобен в использовании. Используется для доказательства формулы корней квадратного уравнения. (Обратить внимание на возможность пойти иным путем, применяя формулу разности квадратов).

Метод “переброски” старшего коэффициента

Суть метода состоит в то, что корни квадратных уравнений

ax² + bx + c = 0 и y²+by+ac=0

связаны соотношениями:

и 

В некоторых случаях удобно решать сначала не данное уравнение

ax² + bx + c = 0, а приведенное y²+by+ac=0 ,которое получается из данного “переброской” коэффициента а, а затем разделить найденные корни на а для нахождения корней исходного уравнения.

Пример: решите уравнение: 

2х²-9х-5=0

заменим приведенным квадратным уравнением с “переброской” коэффициента а:

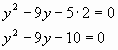
( D>0 ), по теореме, обратной теореме Виета, подбором найдем корни

вернемся к корням исходного уравнения

Ответ: 5; -0,5

 Замечание: метод хорош для квадратных уравнений с “удобными” коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.

Следующие два метода также применимы при определенных условиях и позволяют избежать громоздких вычислений.

Если в квадратном уравнении a+b+c=0, то один из корней равен 1, а второй, по теореме Виета, равен .

Пример: решите уравнение:

157х²+20х-177=0

a = 157, b = 20, c = -177

a + b+ c =157+20-177=0

x₁ = 1,

x₂ = =

Ответ: 1; 

 Если в квадратном уравнении a+c=b, то один из корней равен -1, а второй, по теореме Виета, равен 

Пример: решите уравнение:

203х²+220х+17=0

a = 203, b = 220, c = 17

a + c = 203 + 17 = 220 = b

х₁ = -1,

Ответ: -1; 

Вывод: при решении квадратного уравнения стандартного вида полезно сначала проверить, являются ли числа 1 и -1 корнями уравнения.

Однако, при выборе пути решения квадратного уравнения следует помнить, что помимо специальных методов возможно применение и общих методов решения уравнений.

К таким методам относятся:

• разложение на множители;
• введение новой переменной;
• графический способ.

Презентация общих методов решения уравнений

Метод разложения на множители

Цель: Привести квадратное уравнение общего вида к виду А(х)·В(х)=0, где А(х) и В(х) – многочлены относительно х.

Способы:

• вынесение общего множителя за скобки;
• использование формул сокращенного умножения;
• способ группировки. 

Пример: решите уравнение:

3х²+2х-1=0

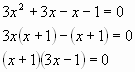
произведение двух множителей равно нулю, если хотя бы один из них равен нулю, а второй при этом не теряет смысла, или когда оба равны нулю.

,

или

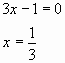
Ответ: -1; .

Метод введения новой переменной

Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.

Пример: решите уравнение:

Пусть: t = 5х + 3

Произведем замену переменной:

(Устно проверим условие D > 0)

по теореме, обратной теореме Виета,

t₁ = 1, t₂ = 2

Произведем обратную замену и вернемся к переменной х:

Если t = 1, то

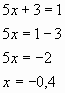
Если t = 2, то

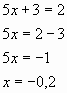
Ответ: -0,4; -0,2

Вывод: при решении уравнения не следует торопиться выполнять преобразования. Посмотрите, нельзя ли записать уравнение проще, введя новую переменную.

И, наконец, наиболее “зрелищный” метод.

Графический метод

Для решения уравнения f(x) = g(x) необходимо построить графики функций 
y = f(x), y = g(x) и найти точки их пересечения; абсциссы точек пересечения и будут корнями уравнения. Вспомним применение этого метода при решении квадратного уравнения:

(Устно обсудить области определения.)

1.     Построим график функции 

Графиком является парабола, “ветви” которой направлены вверх,(0;0) – вершина параболы, график симметричен относительно оси ординат

2.     Построим график функции y = x + 2

Линейная функция. Графиком является прямая.

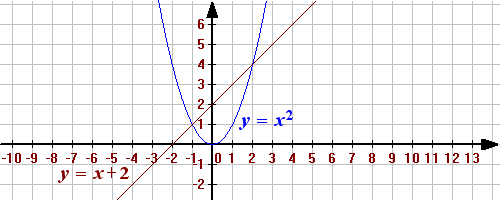
3.    Точки пересечения: А(-1;1) и В(2;4)

Ответ: -1;2

Применяя графический метод в данном случае, мы нашли точное значение корней, но так бывает не всегда. Однако графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.

Историческая справка

Посмотрите на многообразие методов решения. Как, когда, сразу ли появилось такое многообразие? Как много вопросов…

Безусловно, человечество “додумалось” до всего не сразу и не в одночасье. Для этого потребовались долгие годы и даже столетия. Обратимся к историческому путеводителю. Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными относятся ко второму тысячелетию до н.э. Это эпоха расцвета Вавилонии и Древнего Египта. Первое тысячелетие н.э. – Римские завоевательные войны. К этому периоду относится творчество Диофанта. Его трактат “Арифметика” содержит ряд задач, решаемых при помощи квадратных уравнений. В IX веке узбекский математик Аль-Хорезми в Трактате “Алгебра” классифицирует квадратные уравнения. Для нас это время знаковое тем, что приблизительно в это время образуется древнерусское государство Киевская Русь. Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению. И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым он заложил основы буквенной алгебры.

Более подробно с этапами развития методов решения квадратных уравнений, а так же личностью Виета и его вклада в развитие алгебры мы сможем познакомиться на конференции.

Подведение итогов.

Итак, подведем итог. Решение квадратных уравнений возможно осуществлять разными методами. Для квадратных уравнений применимы не только традиционные и специальные методы решения, но и общие методы решения уравнений. Сегодня мы обобщили опыт решения квадратных уравнений и посмотрим, как научились выбирать наиболее рациональный метод решения. Попробуйте расшифровать высказывание из копилки “Золотых мыслей”. Для этого проанализируйте представленные уравнения, выберите для каждого более рациональный метод решения и укажите номер этого метода. Затем, согласно ключу, расставьте в нижней таблице слоги и прочтите высказывание.

Итак, получили высказывание Я. А. Коменского: “Учиться нелегко, но интересно”. Я думаю, эти слова как нельзя, кстати, подходят для окончания нашей сегодняшней презентации.

Домашнее задание

1.    Решите уравнение х²+6х-16=0 по формуле, выделением квадрата двучлена и графическим методом.

2.    Составьте уравнения на применение теорем (метод 9, 10).

3.    Решите уравнение 3х²+5х+2=0 пятью способами.

4.    Решите уравнение (х²-х)²-14(х²-х)+24=0 методом введения новой переменной.

“Золотые мысли” (контроль)

Расставьте номера методов решения уравнений и расшифруйте высказывание.

КЛЮЧ

Пригласительный билет (контроль)

Скачано с www.znanio.ru