
Е. В. Андреева Л. Л. Босова И. Н. Фалина
з п Е к т и в
МАТЕМАТИЧЕСКИЕ основы
ИНФОРМАТИКИ
Учебное пособие
I=10g2N
1/3=0,13
БИНОМ
Е. В. Андреева Л. Л. Босова И. Н. Фалина
МАТЕМАТИЧЕСКИЕ основы
ИНФОРМАТИКИ
Издание подготовлено при содействии
НФПК — Национального фонда подготовки кадров

Москва
БИНОМ. Лаборатория знаний
2005
удк 004.9
БЫС 32,97
Аб5
Андреева Е. В.
Аб5 Математические основы информатики. Элективный курс: Учебное пособие / Е. В. Андреева, Л. Л. Босова, И. Н. Фалина — М.: БИНОМ. Лаборатория знаний,
2005 — 328 с.: ил.
![]() ISBN 5-94774-139-3
ISBN 5-94774-139-3
Учебное пособие входит в УМК для старших классов наряду
с методическим пособием и хрестоматией, Материал раскрывает взаимосвязь
математики и информатики, показывает, как развитие одной из этих научных
областей стимулировало развитие другой. Дается углубленное ![]() представление о математическом
аппарате, используемом в информатике, показывается, как теоретические
результаты, полученные в математике, послужили источником новых идей и
результатов в теории алгоритмов, программировании и в других разделах информатики.
представление о математическом
аппарате, используемом в информатике, показывается, как теоретические
результаты, полученные в математике, послужили источником новых идей и
результатов в теории алгоритмов, программировании и в других разделах информатики.
Для учащихся старших классов информационно-технологического, физико-математического и естественно-научного профилей, желающих расширить свои теоретические представления о математике в информатике и информатике в математике.
удк 004.9 ББК 32.97
Учебное издание
Андреева Елена Владимировна Босова Людмила Леонидовна Фалина Ирина Николаевна
МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ
Элективный курс
Учебное пособие
Ведущий редактор О. Полежаева. Художник Ф. Инфантэ
Художественный редактор О. Лапко. Компьютерная верстка В. Носенко
Подписано в печать 03.10.05. Формат 60х90 1 16. Бумага офсетная. Печать офсетная. Усл. печ. л. 20,5. Тираж 5000 экз. Заказ 3931
Издательство «БИНОМ. Лаборатория знаний». Телефон (095)955-0398. E-mail: Lbz@aha.ru http:\\www.Lbz.ru
Отпечатано с готовых диапозитивов в
полиграфической фирме «Полиграфист» . ![]() 160001, г. Вологда, ул. Челюскинцев, З.
160001, г. Вологда, ул. Челюскинцев, З.
© Андреева Е. В., Босова Л. Л., Фалина И.
ISBN 5-94774-139-3 © БИНОМ. Лаборатория Н., 2005 знаний, 2005
Оглавление
![]()
От авторов![]()
Глава 1. Системы счисления![]()
S 1.1. Позиционные системы счисления. Основные
определения
![]() Вопросы и задания
Вопросы и задания
![]() S 1.2. Единственность представления
чисел в Р-ичных системах счисления Вопросы и задания
S 1.2. Единственность представления
чисел в Р-ичных системах счисления Вопросы и задания
![]() 1.3. Представление произвольных
чисел в позиционных системах счисления
1.3. Представление произвольных
чисел в позиционных системах счисления![]()
1.3.1. Развернутая и свернутая формы записи. . . . . . . 2![]()
1.3.2. Перечисление натуральных чисел![]()
1.3.3. Представление обыкновенных
десятичных дробей в Р-ичных системах счисления . . . . . . . .![]()
Вопросы и задания![]()
![]() 1.4. Арифметические операции в
Р-ичных системах счисления
1.4. Арифметические операции в
Р-ичных системах счисления
 1.4.1. Сложение
1.4.1. Сложение
1.4.2. Вычитание
1.4.3. Умножение
1.4.4. Деление
Вопросы и задания
S 1.5. Перевод чисел из Р-ичной системы счисления в десятичную
1.5.1. Перевод целых Р-ичных чисел
1.5.2. Перевод конечных Р-ичных дробей 1.5.3. Перевод периодических Р-ичных дробей .
Вопросы и задания
S 1.6. Перевод чисел из десятичной системы счисления в Р-ичную .
1.6.1. Два способа перевода целых чисел . . . . . . .
1.6.2. Перевод конечных десятичных дробей. .
Вопросы и задания
S 1.7. Смешанные системы счисления
Вопросы и задания
4 Оглавление
![]()
|
S 1.8. Системы счисления и архитектура компьютеров 1.8.1. Использование уравновешенной троичной |
|
|
системы счисления 1.8.2. Использование Фибоначчиевой системы |
. 56 |
|
счисления |
. 58 |
|
1.8.3. Недвоичные компьютерные арифметики |
. 60 |
|
Вопросы и задания |
. 61 |
|
Заключение |
. 61 |
|
Глава 2. Представление информации в
компьютере |
• 63 |
|
S 2.1. Представление целых чисел |
. 65 |
|
2.1.1. Представление целых положительных чисел |
. 66 |
|
2.1.2.
Представление целых отрицательных чисел . 2.1.3. Перечисление чисел в целочисленной |
. 68 |
|
компьютерной арифметике 2.1.4. Особенности реализации арифметических |
. 71 |
|
операций в конечном числе разрядов . |
. 73 |
|
Вопросы и задания |
. 74 |
|
S 2.2. Представление вещественных чисел |
. 74 |
|
2.2.1. Нормализованная запись числа 2.2.2. Представление вещественных чисел |
. 75 |
|
в формате с плавающей запятой 2.2.3. Выполнение арифметических операций |
. 80 |
|
над вещественными числами 2.2.4. Особенности реализации вещественной |
|
компьютерной арифметики
Вопросы и задания
S 2.3. Представление текстовой информации Вопросы и задания
S 2.4. Представление графической информации
2.4.1. Общие подходы к представлению
в компьютере информации естественного происхождения .![]()
 2.4.2. Векторное и растровое
представление графической информации .
2.4.2. Векторное и растровое
представление графической информации .![]() . 102 2.4.3. Квантование цвета . . .
104
. 102 2.4.3. Квантование цвета . . .
104
2.4.4. Цветовая модель RGB
2.4.5. Цветовая модель СМУК .
2.4.6. Цветовая модель HSB. .
Вопросы и задания. . . . . .
S 2.5. Представление звуковой информации
2.5.1. Понятие звукозаписи . . . . . 122
2.5.2. Импульсно-кодовая модуляция .
2.5.3. Формат MIDI .
Оглавление
![]()
2.5.4. Принципы компьютерного воспроизведения
звука
Вопросы и задания
S 2.6. Методы сжатия цифровой информации
2.6.1. Алгоритмы обратимых методов .
![]() 2.6.2. Методы сжатия с регулируемой
потерей
2.6.2. Методы сжатия с регулируемой
потерей
информации
Вопросы и задания
Заключение ![]() . 145
. 145
Глава З. Введение в алгебру логики![]()
S 3.1. Алгебра логики. Понятие высказывания . . . . . . . 148 Вопросы и задания

![]() 3.2. Логические операции. Таблицы истинности Вопросы
и задания S 3.3.
3.2. Логические операции. Таблицы истинности Вопросы
и задания S 3.3.
Вопросы и задания
![]() Методы решения логических задач . 168
Методы решения логических задач . 168
Вопросы и задания
 S 3.5. Алгебра переключательных схем
S 3.5. Алгебра переключательных схем
Вопросы и задания
S 3.6. Булевы функции![]() . 176
Вопросы и задания
. 176
Вопросы и задания![]()
S 3.7. Канонические формы логических формул.
Теорема о СДНФ
![]() Вопросы и задания
Вопросы и задания
S 3.8. Минимизация булевых функций в
классе дизъюнктивных нормальных форм![]() . 185 Практические задания
. 185 Практические задания![]() . 189
. 189
S 3.9. Полные системы булевых функций![]() . 190
. 190
Вопросы и задания![]() . 192
. 192
![]() S 3.10. Элементы схемотехники. Логические схемы .
193
S 3.10. Элементы схемотехники. Логические схемы .
193
Заключение
Глава 4. Элементы теории алгоритмов![]() . 199
. 199
S 4.1. Понятие алгоритма. Свойства алгоритмов .![]() . 200
. 200
Вопросы и задания![]() . 208
. 208
S 4.2. Уточнение понятия алгоритма. Машина Тьюринга . . 209
4.2.1. Необходимость уточнения понятия алгоритма . 209
![]() 4.2.2. Описание машины Тьюринга
4.2.2. Описание машины Тьюринга
4.2.3. Примеры машин Тьюринга
![]() Формальное описание алгоритма.
Формальное описание алгоритма.
Математическое описание машины Тьюринга . 218
6 Оглавление
![]()
Вопросы и
задания. . ![]() . 220
. 220
S 4.3. Машина Поста как уточнение понятия алгоритма . . . 220
|
Вопросы и задания. . . . . |
|
|
S 4.4. Алгоритмически неразрешимые задачи |
|
|
и вычислимые функции. . |
|
|
Вопросы и задания. . |
|
|
S 4.5. Понятие сложности алгоритма . . . |
|
|
Вопросы и задания. . |
|
|
S 4.6. Анализ алгоритмов поиска . . . . . |
|
|
4.6.1. Последовательный поиск в неупорядоченном |
|
|
массиве |
|
|
4.6.2. Алгоритм бинарного поиска в упорядоченном |
|
|
массиве |
|
|
Вопросы и задания. . . . . |
|
|
S 4.7. Анализ алгоритмов сортировки |
|
|
4.7.1. Обменная сортировка методом «пузырька» |
|
|
4.7.2. Сортировка выбором |
|
|
4.7.3. Сортировка вставками . . . . . . |
|
|
4.7.4. Сортировка слиянием. . . . . |
|
|
Вопросы и задания |
|
|
Заключение . . |
|
|
Глава 5. Основы теории информации.
. . . . . . . . . . . . . . |
|
|
S 5.1. Понятие информации. Количество информации. |
|
|
Единицы измерения информации |
. 250 |
|
Вопросы и задания S 5.2. Формула Хартли определения количества |
. 254 |
|
|
. 254 |
|
Вопросы и задания. . . . . |
. 260 |
|
S 5.3. Применение формулы Хартли . |
. 261 |
|
Вопросы и задания. . . . . . . S 5.4. Закон аддитивности информации. Алфавитный |
. 265 |
|
подход к измерению информации |
. 266 |
|
Вопросы и задания. . . . . |
. 269 |
S 5.5. Информация и вероятность. Формула Шеннона . . . . . 269
|
Вопросы и задания. . . . . S 5.6. Оптимальное кодирование информации |
|
|
и ее сложность . . . . . . . |
|
|
Вопросы и задания. . . . . |
|
|
Заключение . . . . . . |
|
Глава 6. Математические основы вычислительной геометрии и
компьютерной графики. . . . . .![]() . 283 S 6.1. Координаты и векторы на
плоскости .
. 283 S 6.1. Координаты и векторы на
плоскости .![]() . 285
. 285
Оглавление 7
![]()
Вопросы и задания. . . . . . . . .![]() . 292
. 292
6.2. Способы описания линий на плоскости. . . .![]() . 292
. 292
6.2.1. Общее уравнение прямой . . . . , . .![]() . 292
. 292
6.2.2. Нормированное уравнение прямой. . . . . . . . . . 294
6.2.3. Параметрические уравнения прямой, луча ![]() отрезка. . . . . .
отрезка. . . . . .![]() . 296 6.2.4. Способы описания
окружности .
. 296 6.2.4. Способы описания
окружности .![]() . 297
. 297
Вопросы и задания. . . . .![]() . 298
. 298
S 6.3. Задачи компьютерной графики на
взаимное расположение точек и фигур .![]() . 298 6.3.1. Прямая, перпендикулярная
данной и проходящая через заданную точку .
. 298 6.3.1. Прямая, перпендикулярная
данной и проходящая через заданную точку .![]() . 298 6.3.2. Расположение точки
относительно прямой, луча или отрезка . . . . . .
. 298 6.3.2. Расположение точки
относительно прямой, луча или отрезка . . . . . .![]() . 299
. 299
6.3.3. Взаимное расположение прямых,
отрезков, лучей . .![]() . 301
. 301
![]() 6.3.4. Взаимное расположение
окружности и прямой
6.3.4. Взаимное расположение
окружности и прямой![]() . зоз
. зоз
6.3.5. Взаимное расположение двух окружностей . . . 305
Вопросы и задания![]() . 307 S 6.4.
Многоугольники
. 307 S 6.4.
Многоугольники![]() . 307
. 307
6.4.1. Проверка выпуклости многоугольника . 308
6.4.2. Проверка принадлежности точки
внутренней области многоугольника![]() . 308
. 308
6.4.3. Вычисление площади простого многоугольника . .![]() . 310 Вопросы и задания. . . . . .
. 310 Вопросы и задания. . . . . .![]() . 311
. 311
S 6.5. Геометрические объекты в пространстве![]() . 312
. 312
6.5.1. Основные формулы![]() . 312
. 312
6.5.2. Определение пересечения прямой
линии и треугольника в пространстве![]()
![]() 6.5.3. Вращение точки вокруг заданной прямой в
пространстве
6.5.3. Вращение точки вокруг заданной прямой в
пространстве![]() . 315 Вопросы и задания
. 315 Вопросы и задания![]() . 317
. 317
Заключение . -. . . . . . . .![]() . 318
. 318
Приложение .
. .![]() . . . . . . . 319
. . . . . . . 319
Предметный
указатель . . . . . . . . . . . . . .![]() . . . е . . . . 320
. . . е . . . . 320
От авторов
![]()
Дорогие старшеклассники!
Задумывались ли вы, почему в современных компьютерах используется двоичная система счисления и можно ли заменить ее какой-либо другой?
Знаете ли вы, что такое машина Тьюринга и почему знакомству с ней придают такое важное значение в теории алгоритмов?
Вы, конечно, знаете, что для записи в компьютере графической информации используется растровое и векторное представление. А можно ли любую фотографию сохранить в компьютере так, чтобы ее цифровое представление было абсолютно идентичным оригиналу?
А из каких элементов построен компьютер, ведь известно, что компьютер обрабатывает только двоичные данные, но при этом является универсальным исполнителем?
До какого уровня можно улучшать алгоритмы, например, сортировки, чтобы они работали как можно быстрее?
На эти и многие другие вопросы вы найдете ответы в данной книге. Каждый ответ на подобный вопрос — это результат гениальной догадки и длительной работы ученых по разработке математической теории, на основе которой удалось обосновать выдвинутое предположение.
Наша книга новый профильно-ориентированный курс «Математические основы информатики», который поможет вам продолжить образование в области математики, информатики и информационных технологий.
Сегодня, в начале XXI века, человечество
входит в новую цивилизацию — цивилизацию, связанную с проникновением
компьютеров во все сферы жизнедеятельности человека. Эту цивилизацию называют
информационной, виртуальной, компьютерной.![]()
Вы будете жить в новой цивилизации и должны научиться жить в ней, не теряя себя, пользоваться ее благами, но не становиться зависимыми от них. Мы убеждены, что человек может сохранить себя как homo sapi-
От авторов 9
ens, только изучая основы фундаментальных знаний о мире, который его окружает. Особое значение в современных условиях приобретает такая учебная дисциплина, как информатика. В данной книге мы хотим показать, как математический аппарат используется в информатике, какие достижения математики повлияли на становление и развитие информатики с одной стороны, а с другой стороны, какие задачи информатики дали толчок к появлению новых идей и методов в математике. Это взаимовлияние двух наук продолжается до сих пор.
Мы хотели вам показать, как сложно выдвигать новые гипотезы, как часто ученые шли десятилетиями и даже столетиями к тем результатам, которые для вас сегодня привычны и очевидны.
![]()
![]()
![]()
![]()
![]()
![]() В
подготовке этой книги участвовал большой коллектив. Многие преподаватели СУНЦ
МГУ (физико-математической школы—интерната им. А. Н. Колмогорова) использовали
предварительные варианты книги на своих занятиях со школьниками и предложили
различные улучшения. В написании книги большую помощь оказали наши коллеги: В.
В. Усатюк (глава 2), Е. В. Щепин (глава 5), Ю. Е. Егоров (глава 6). Мы выражаем
им глубокую благодарность. Мы благодарим за внимательное прочтение и научные
консультации преподавателей факультета ВМиК МГУ им. М. В. Ломоносова В. Б,
Алексеева (главы З и 4) и А. И. Фалина (глава 6). И, конечно же, мы благодарны
самой многочисленной группе наших соавторов — ученикам СУНЦ МГУ, которые
слушали лекции по материалам глав книги, самыми первыми решали все наши задачи
и спрашивали, спрашивали, спрашивали... еще во время написания книги.
В
подготовке этой книги участвовал большой коллектив. Многие преподаватели СУНЦ
МГУ (физико-математической школы—интерната им. А. Н. Колмогорова) использовали
предварительные варианты книги на своих занятиях со школьниками и предложили
различные улучшения. В написании книги большую помощь оказали наши коллеги: В.
В. Усатюк (глава 2), Е. В. Щепин (глава 5), Ю. Е. Егоров (глава 6). Мы выражаем
им глубокую благодарность. Мы благодарим за внимательное прочтение и научные
консультации преподавателей факультета ВМиК МГУ им. М. В. Ломоносова В. Б,
Алексеева (главы З и 4) и А. И. Фалина (глава 6). И, конечно же, мы благодарны
самой многочисленной группе наших соавторов — ученикам СУНЦ МГУ, которые
слушали лекции по материалам глав книги, самыми первыми решали все наши задачи
и спрашивали, спрашивали, спрашивали... еще во время написания книги.
Книга, на наш взгляд, будет интересна и полезна тем, кто интересуется математикой, информатикой, физикой. Мы надеемся, что она поможет вам в выборе будущей профессиональной деятельности. Однако читать и изучать ее будет непросто, хотя мы максимально пытались структурировать материал, включили много иллюстраций, примеров. Не страшно, если вы не сможете разобраться в чем-то при первом чтении, возможно, к содержанию некоторых параграфов вам придется вернуться позже. Но, как говорится, дорогу осилит идущий.
Авторы
От авторов
![]()
Как работать с книгой![]()
Книга «Математические основы информатики» состоит из 6 глав, которые, вообще говоря, можно читать и изучать в любом порядке. Материал некоторых глав взаимосвязан, и в тексте есть соответствующие ссылки.
Главы состоят из параграфов, после каждого параграфа есть вопросы и задания для самостоятельной работы.
В тексте параграфов вам будут встречаться вопросы и задания, ответы на которые даны там же. Все эти вопросы не очень простые, но не спешите читать ответы и решения, попробуйте сначала самостоятельно найти ответы к поставленным проблемам.
![]() В тексте много рисунков и таблиц, как
правило, они
В тексте много рисунков и таблиц, как
правило, они ![]() содержат обобщающий материал в
графическом виде, каждый раз старайтесь понять, почему приведен именно этот
рисунок и именно в таком виде. Такая работа с иллюстративным материалом поможет
вам лучше понять излагаемый материал.
содержат обобщающий материал в
графическом виде, каждый раз старайтесь понять, почему приведен именно этот
рисунок и именно в таком виде. Такая работа с иллюстративным материалом поможет
вам лучше понять излагаемый материал. ![]()
![]() Наиболее важный
материал мы выделили навигационным знаком. Этот знак поможет вам быстро
находить наиболее существенные факты, облегчит работу с книгой.
Наиболее важный
материал мы выделили навигационным знаком. Этот знак поможет вам быстро
находить наиболее существенные факты, облегчит работу с книгой.
Текст книги непростой, некоторые
разделы или па![]() раграфы, скорее всего, придется читать
несколько раз, пусть вас это не смущает, именно так изучается серьезная
профессиональная литература.
раграфы, скорее всего, придется читать
несколько раз, пусть вас это не смущает, именно так изучается серьезная
профессиональная литература.
В тексте курсивом выделены вводимые термины и понятия, все они внесены в предметный указатель, который находится в конце книги. Обязательно используйте его для поиска нужных терминов и определений, это облегчит вам работу с книгой.
Успехов вам, дорогие ребята, в изучении книги!
Глава 1 ![]()
![]()
Системы счисления
![]()
Мысль выражать все числа немногими ![]() знаками, придавая им, кроме значения
по форме, еще значение по месту, настолько проста, что именно из-за этой
простоты трудно понять, насколько она удивительна. Как нелегко было прийти к
этому методу, мы видим на примере величайших гениев греческой учености Архимеда
и Аполлония, от которых эта мысль осталась скрытой.
знаками, придавая им, кроме значения
по форме, еще значение по месту, настолько проста, что именно из-за этой
простоты трудно понять, насколько она удивительна. Как нелегко было прийти к
этому методу, мы видим на примере величайших гениев греческой учености Архимеда
и Аполлония, от которых эта мысль осталась скрытой.
П. С. Лаплас
Владея развитой компьютерной теорией, компьютерные специалисты иногда забывают о той роли, которую сыграли системы счисления в истории компьютеров.
А. П. Стахов
S 1.1. Позиционные системы счисления. Основные определения
S 1.2. Единственность представления чисел в Р-ичных системах счисления
S 1.3. Представление произвольных чисел в позиционных системах счисления
S 1.4.Арифметические операции в Р-ичных системах счисления
S 1.5. Перевод чисел из Р-ичной системы счисления в десятичную
S 1.6. Перевод чисел из десятичной системы счисления в Р-ичную
S 1.7. Смешанные системы счисления
S 1.8. Системы счисления и архитектура компьютеров
![]()
ервые счетные приборы (абаки, счеты), прообразы современных компьютеров, начали создаваться задолго до возникновения и алгебры логики, и теории алгоритмов. И определяющую роль в их конструкции играли выбранные для них системы счисления.
 Первые механические
счетные машины (суммирующая машина Блеза Паскаля — 1642 г., счетная машина
Вильгельма Лейбница — 1673 г., аналитическая машина Чарльза Бэббиджа — 1848 г.)
были разработаны на основе десятичной системы счисления. Для реализации десяти
устойчивых состояний использовались сложные системы зубчатых колес. Эти
механические машины были очень громоздки, занимали много места. Так, если бы
проект Аналитической машины Бэббиджа, которая яви
Первые механические
счетные машины (суммирующая машина Блеза Паскаля — 1642 г., счетная машина
Вильгельма Лейбница — 1673 г., аналитическая машина Чарльза Бэббиджа — 1848 г.)
были разработаны на основе десятичной системы счисления. Для реализации десяти
устойчивых состояний использовались сложные системы зубчатых колес. Эти
механические машины были очень громоздки, занимали много места. Так, если бы
проект Аналитической машины Бэббиджа, которая яви![]() лась механическим
прототипом появившихся спустя столетие ЭВМ, был реализован, то по размерам
машина сравнялась бы с локомотивом, и чтобы привести в движение ее устройства,
понадобился бы паровой двигатель. Причинами этого были механический принцип
построения устройств и использование десятичной системы счисления, затрудняющей
создание простой элементной базы. Через 63 года после смерти Бэббиджа немецкий
студент Конрад Цузе начал работу по созданию машины, основанной на принципах
действия Аналитической машины Бэббиджа. В 1937 г. машина Z1 была готова.
Работала она на основе двоичной системы счисления и была чисто механической,
как у Бэббиджа. Но использование двоичной системы сотворило чудо машина
занимала Конрад цузе всего два квадратных метра на столе в квар(1910—1985) тире
изобретателя.
лась механическим
прототипом появившихся спустя столетие ЭВМ, был реализован, то по размерам
машина сравнялась бы с локомотивом, и чтобы привести в движение ее устройства,
понадобился бы паровой двигатель. Причинами этого были механический принцип
построения устройств и использование десятичной системы счисления, затрудняющей
создание простой элементной базы. Через 63 года после смерти Бэббиджа немецкий
студент Конрад Цузе начал работу по созданию машины, основанной на принципах
действия Аналитической машины Бэббиджа. В 1937 г. машина Z1 была готова.
Работала она на основе двоичной системы счисления и была чисто механической,
как у Бэббиджа. Но использование двоичной системы сотворило чудо машина
занимала Конрад цузе всего два квадратных метра на столе в квар(1910—1985) тире
изобретателя.
В современных компьютерах вся информация также хранится в виде последовательностей нулей и единиц. Однако двоичная система счисления в чистом виде обладает рядом принципиальных недостатков, которые становятся критичными в век бурного развития компьютерной техники. Главными из этих недостатков являются проблема представления отрицательных чисел и «нулевая избыточность» (т. е. отсутствие избыточности, из чего вытекает невозможность определения, произошло ли искажение информации при ее передаче — см. S 1.8). Практическая потребность в решении этих вопросов вызывает сегодня по-
вышенный интерес к способам представления информации в компьютере и новым компьютерным арифметикам. Так, например, родоначальник теории информации Джон фон Нейман доказал теорему о том, что троичная система счисления позволяет наиболее эффективно среди всех основных позиционных систем счисления «сворачивать» информацию о вещественном числе.
Какие же системы счисления рассматриваются математиками и инженерами в качестве «компьютерных»? Какими свойствами должна обладать система счисления, при помощи которой будет кодироваться информация в компьютерных системах? Мы попытаемся ответить на эти и другие вопросы, связанные с системами счисления. Наша задача — рассмотреть принципы построения позиционных систем счисления, познакомиться с неклассическими (нетрадиционными) позиционными системами счисления, с системами счисления, используемыми в компьютерах.
Начнем с повторения базовых определений.
![]()
Определение 1. Система счисления или нумерация это способ записи (обозначения) чисел.
Определение 2. Символы, при помощи
которых записываются числа, называются цифрами, а их совокупность ![]() алфавитом
системы счисления. Количество цифр, составляющих алфавит, называется его
размерностью.
алфавитом
системы счисления. Количество цифр, составляющих алфавит, называется его
размерностью.
Определение З. Система счисления называется позиционной, если количественный эквивалент цифры зависит от ее положения в записи числа.
В привычной нам десятичной системе значение числа образуется следующим образом: значения цифр умножаются на «веса» соответствующих разрядов и все полученные значения складываются. Например, 5047 = 5' 1000 + + 0100 + 4•10 + 7•1. Такой способ образования значения числа называется аДДитивно-мультипликативным.
Определение 4. Последовательность чисел, каждое из которых задает «вес» соответствующего разряда, называется базисом позиционной системы счисления.
![]() Основное достоинство практически любой позиционной системы
счисления — возможность записи произвольного числа при помощи ограниченного
количества символов.
Основное достоинство практически любой позиционной системы
счисления — возможность записи произвольного числа при помощи ограниченного
количества символов.
Определение 5. Позиционную систему счисления называют традиционной, если ее базис образуют члены геометрической прогрессии, а значения цифр есть целые неотрицательные числа.
Так, базисы десятичной, двоичной и
восьмеричной систем счисления образуют геометрические прогрессии со
знаменателями 10, 2 и 8 соответственно. В общем виде базис традиционной системы
счисления можно за![]() писать так:
писать так:
-3 -2 -1![]()
В Р-ичных системах размерность алфавита равна основанию системы счисления.
Так, алфавит десятичной системы
составляют цифры О, 1, 2, З, 4, 5, 6, 7, 8, 9. Алфавитом произвольной системы
счисления с основанием Р служат числа О, 1, ![]() Р—1, каждое из
которых должно быть записано с помощью одного уникального символа, младшей
цифрой всегда является О.
Р—1, каждое из
которых должно быть записано с помощью одного уникального символа, младшей
цифрой всегда является О.
В класс позиционных систем счисления входят также системы, в которых либо базис не является геометрической прогрессией, а цифры есть целые НеОТРИЦательные числа, либо базис является геометрической прогрессией, но цифры не являются целыми неотрицательными числами.
К первым можно отнести факториальную и
Фибоначчиеву системы счисления, ко вторым — уравновешенные системы счисления.
Такие системы будем называть нетрадиционными. Алфавитом Фибоначчиевой системы
являются цифры О и 1, а ее базисом — последовательность чисел Фибоначчи 1, 2,
З, 5, 8, 13, 21, 34, 55, 89![]()
Леонардо Пизанский Фибоначчи (1170—1250) итальянский математик. Благодаря его книге «Liber Abaci» Европа узнала индо-арабскую систему чисел, которая позднее вытеснила римские числа
Базисом факториальной системы счисления
является последовательность 1!, 2'![]() В отношении алфавита этой системы можно
сделать замечание: количество цифр, используемых в разряде, увеличивается с
ростом номера разряда.
В отношении алфавита этой системы можно
сделать замечание: количество цифр, используемых в разряде, увеличивается с
ростом номера разряда.
В общем случае, если система счисления
устроена та![]() ким образом, что основание как таковое в
ней отсутствует, а базис представляет собой последовательность чисел
ким образом, что основание как таковое в
ней отсутствует, а базис представляет собой последовательность чисел ![]() то
количество Ук цифр, используемых в К-м разряде, определяется так:
то
количество Ук цифр, используемых в К-м разряде, определяется так:
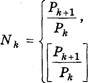 если РК
+1'. ;
если РК
+1'. ;
+ 1, в противном случае.
Знак «:» означает «делится нацело».
Пример 1. Приведем сводную таблицу, характеризующую ![]() некоторые
позиционные системы счисления.
некоторые
позиционные системы счисления.
|
Система счисления |
Основание |
Размерность алфавита |
Цифры |
|
Двоичная |
2 |
2 |
|
|
Троичная |
|
з |
|
|
Восьмеричная Шестнадцатеричная |
16 |
16 |
|
|
Факториальная |
Нет |
Увеличивается с ростом номера разряда |
1-й разряд: О, 1 2-й разряд: 0, 1, 2 3-й разряд: О, 1, 2, З |
|
Фибоначчиева |
Нет |
2 |
|
|
Уравновешенная троичная (см. S 1.8) |
з |
з |
|
Основанием Р-ичной системы счисления
может быть ![]() любое натуральное число, большее единицы.
Системой счисления с минимальным основанием является двоичная система, все
числа в которой записываются с помощью 0 и 1.
любое натуральное число, большее единицы.
Системой счисления с минимальным основанием является двоичная система, все
числа в которой записываются с помощью 0 и 1.
Пример 2. Приведем запись некоторых десятичных чисел в различных нетрадиционных позиционных системах счисления.

![]()
позиционную систему счисления:
1) фазис, алфавит, основание}; 2) фазис, алфавиту; З) {базис}?
Ответ. Оказывается, что для
однозначного определения позиционной системы счисления, у которой в качестве
цифр используются натуральные числа и 0, необходимо и достаточно указать только
ее базис: последовательность чисел ..., Р о, Р![]() Все остальные
компоненты системы являются производными от базиса. Покажем это.
Все остальные
компоненты системы являются производными от базиса. Покажем это.
Формулировка необходимого условия имеет вид: если задана позиционная система счисления, то, следовательно, задан базис. Это утверждение очевидно следует из определений З и 4.
Формулировка достаточного условия имеет вид: если задан базис, то задана позиционная система счисления,
![]() Рассмотрим отдельно
два случая: 1) базис является геометрической прогрессией, 2) базис не является
геометрической прогрессией.
Рассмотрим отдельно
два случая: 1) базис является геометрической прогрессией, 2) базис не является
геометрической прогрессией.
![]()
янно и равно Р — основанию системы счисления. Количество цифр в алфавите также равно Р, так как максимальное число единиц, которое можно записать в любом разряде, равно Р—1, а минимальным числом является О.
Во втором случае основание в системе
отсутствует, а количество цифр алфавита в каждом разряде опреде![]() ляется по
базису согласно формуле (1.1).
ляется по
базису согласно формуле (1.1).
Если же в качестве цифр в системе счисления используются числа, отличные от целых неотрицательных, то для определения системы счисления необходимо еще описать и ее алфавит.
Вопрос. Какая последовательность чисел может быть использована 6 качестве базиса позиционной системы счисления?
Ответ. Последовательность чисел может являться базисом позиционной системы счисления только тогда, когда в соответствующей этому базису системе может быть представлено любое число (если система предназначена только для нумерации целых чисел, то любое целое число).
Для представления целых чисел достаточно
взять любую бесконечную монотонно возрастающую числовую последовательность (Ро,
Р Р., ...), начинающуюся с единицы (Ро = 1). В качестве цифр К-го разряда этой
системы следует использовать символы, обозначающие числа О, 1, 2, ..., ЛТк—1,
где вычисляется по формуле (1.1). Числа О и 1 в любой из таких систем
представляются соответствующими цифрами. Пусть числа 2, . ![]() представимы
в системе с описанным базисом. Покажем, что тогда и число а + 1 также
представимо.
представимы
в системе с описанным базисом. Покажем, что тогда и число а + 1 также
представимо.
Если младшая цифра числа а меньше, чем — 1, то в представлении числа а + 1 все старшие цифры совпадают с цифрами а, а младшая цифра на единицу больше, чем соответствующая цифра числа а. Так как Ро = 1, то, согласно аддитивно-мультипликативному принципу построения подобных систем, числа а и а + 1 в системе с данным базисом в этом случае действительно отличаются на единицу. Пусть теперь в представлении числа а в разрядах О, 1, 2 i стоят максимально допустимые цифры этих разрядов, а цифра в (i + 1)-м разряде меньше, чем — 1. Увеличим значение числа, состоящего из цифр, стоящих в разрядах 0, 1, 2, i числа а, на единицу. Получившееся число можно оценить снизу и сверху так:
S
1 +No-1 + - 1)Р1 + (ЛЬ- 1)Р2 + ... + (N. - ![]()
Здесь при оценке снизу учтено, что согласно формуле (1.1) Рр 2 Р N. •Р. Р. 1, а при оценке сверху используются следующие из той же формулы неравенства — 1 < Таким образом, для числа а + 1
оказывается возможным следующее представление: цифра в (i + 1)-м разряде числа а увеличивается на единицу, а число
О S 1 + No-1 + (N1-1)P1+ (ЛЉ-1)Р2 +...+ (Nr1)P. - Р <
![]()
![]() Р.. Заметим, что если
для любых соседних элементов базиса справедливо точное равенство к
Р.. Заметим, что если
для любых соседних элементов базиса справедливо точное равенство к![]()
![]() то все цифры в представлении а + 1 в
разрядах 0, 1, ..., i равны О. В этом случае можно говорить и о единственности
представления чисел в позиционной системе с соответствующим базисом.
Соответствующая теорема доказана в следующем параграфе.
то все цифры в представлении а + 1 в
разрядах 0, 1, ..., i равны О. В этом случае можно говорить и о единственности
представления чисел в позиционной системе с соответствующим базисом.
Соответствующая теорема доказана в следующем параграфе.
Вопрос. Какие символы могут быть использованы в качестве цифр системы счисления?
Ответ. В качестве цифр систем счисления могут быть использованы любые символы, это наглядно демонстрируют нам ученые, занимающиеся историей математики: вавилоняне использовали клиновидные цифры (у них не было бумаги, и «писали» они на мягких глиняных дощечках); китайцы использовали иероглифы; мы используем арабские цифры. Однако в математике придерживаются следующих договоренностей в отношении вида используемых цифр.
Если основание системы счисления Р меньше 10, то для символьного представления цифр в ней, как правило, используются первые Р десятичных цифр (от 0 до Р — 1). Например, в пятеричной системе счисления будут использоваться пять цифр: О, 1, 2, З, 4.
Для 10 < Р < 37 в качестве первых десяти цифр также обычно используют их десятичное представление, а для остальных цифр — буквы латинского алфавита.
Вопросы и задания
1. Сформулируйте определение аддитивно-мультипликативной системы счисления.
2. Сформулируйте правила, по которым вычисляется значение числа в римской системе счисления. Является ли она аддитивно-мультипликативной?
З. Сколько цифр нужно для записи чисел в двенадцатеричной системе счисления?
4. Верно ли записаны числа в семеричной системе счисления.• 23607, 357217, 608512 ?
5. Предложите собственную классификацию систем счисления.
6. Придумайте и выпишите алфавит для пятидесятеричной системы счисления.
7. Опишите позиционную систему счисления, основанную на разложении числа по степеням простых чисел. Является ли она аддитивно-мультипликативной?
8. Докажите, что для Р-ичных систем счисления минимальным основанием является число 9
S 1 .2. Единственность представления чисел в Р-ичных системах счисления
В примере 2 (5 1.1) были приведены представления чисел 10, 25 и 100 в системах счисления, отличных от десятичной.
Вопрос. Можно ли эти числа записать 6 указанных системах еще и Другим способом или это преДставление еДинственно?
Ответ. Оказывается, что любое десятичное число можно
представить в любой позиционной системе счисления, а для целых чисел в
большинстве систем это можно сделать единственным способом. Докажем это
утверждение ![]() для натуральных чисел в Р-ичных системах
счисления. З
для натуральных чисел в Р-ичных системах
счисления. З
Теорема 1. Пусть Р — произвольное натуральное число, большее единицы. Существует и единственно представление любого натурального числа Х в виде степенного ряда
![]()
Доказательство
Существование. Доказательство основано на методе построения, т. е. для произвольного натурального числа мы просто построим представление вида (1.2).
Так как числа ро , Р 1 , Р 2 , Р з образуют монотонно возрастающую числовую последовательность, то СУП№СТвует такое натуральное число п, что
![]()
Разделим интервал [Р п ; Р+1 ) на Р — 1 равную часть, тогда границами полученных интервалов окажутся числа 1 2 , хр = Р•р п = Р +1 . Длина каждого промежутка [хк ; 1), где К = 1, Р — 1, равна Рп .
Из (1.3) и проведенного построения следует, что число Х попадет в один из интервалов [хк ; 1), т. е. существует такое натуральное К, 1 < К Р, что крп S х < (К + 1)Р П .
Положим а = К < Р. Тогда а![]()
Обозначим разницу между числом Х и левой
границей хк соответствующего интервала как У = Х — а Р п ![]() О S У
Р п по построению.
О S У
Р п по построению.
![]()
![]() Если У = О,
то построение закончено, в противном случае, опять сравнивая уже величину У с
членами возрастающей последовательности 1, Р, Р 2 , Р Рп ,
найдем целое число т такое, что Р Т < У < Рт+1
Если У = О,
то построение закончено, в противном случае, опять сравнивая уже величину У с
членами возрастающей последовательности 1, Р, Р 2 , Р Рп ,
найдем целое число т такое, что Р Т < У < Рт+1
Для номеров т + 1 < i п — 1 положим а.
ких номеров может и не оказаться, если т + 1 = п) и вычислим а . Для этого, как и ранее, разделим интервал [РТ ; РТ +1 ) на Р — 1 равные части длиной РТ и определим, в какую из них попадает число У, т. е. среди целых значений h: О h < Р найдем такое, что
![]() + 1)Р Т .
+ 1)Р Т .
Положим
а = и обозначим Z = У — а Р ![]()
т
И так далее.
В результате получим, что
![]()
где О < а. <Р, ![]() п, а * О.
п, а * О.
Единственность. Для доказательства воспользуемся методом от противного.
Предположим, что некоторое натуральное число имеет два различных представления вида (1.2):
![]() (1.40)
(1.40)
и
Х 2 = ь тР т + Ь т 1 рп 1 + + 61 р + ![]()
Покажем, что если т > п, то Х2 > Х
1. Для доказательства оценим Х2 снизу наименьшим возможным числом (Ь![]()
![]() 1•р
т + 1 + ... + + О = Р Т .
1•р
т + 1 + ... + + О = Р Т .
Оценим Х1 сверху наибольшим возможным числом
![]()
![]() (Р-1)Р П + (Р-1)РП -
1 + ... + (Р-1)? + (Р-1) -
(Р-1)Р П + (Р-1)РП -
1 + ... + (Р-1)? + (Р-1) -
![]()
Здесь для вычисления суммы использовалась формула суммы членов конечной геометрической прогрессии.
Так как по
предположению т п + 1, то Х1 < рп+ 1 Х2![]()
т. е. Х < Х2. Следовательно, если Х = Х2 , то п = т.
Покажем, что а = Ь . Опять воспользуемся методом от
противного. Пусть а Ь (например, ап = Ь + 1). Оценим разность Х1 — Х2 = Р — (а![]()
Заменим все а. (О i п) на их максимально возможные значения (Р — 1), а все Ь. (О i < п) — на минимально возможные значения (нули):
Х1 - Х2 ![]() П-
П-
Это противоречит тому, что Х1 = Х2 , следовательно,
![]()
Пусть существует такое К, что а. = bi при К + 1 S i п = т, но ак Ьк. Сравним числа
![]()
![]()
После преобразования получаем:
![]()
где ак Ьк. Повторив проведенные ранее рассуждения, получим, что У У2 , и, следовательно, Х * Х
![]()
Получили противоречие с исходным предположением о равенстве представлений (1.4, а) и (1.4, Ь). Следовательно, а. = Ь. при О < i < п = т, т. е. представление вида (1.2) для любого натурального числа единственно. Теорема Доказана.
На основании теоремы 1 можно утверждать, что любое натуральное число можно записать в какой угодно Р-ичной системе счисления, причем единственным образом.
Пример З. Построим представление десятичного числа Х = 3056 в виде степенных рядов при различных значениях Р.
1) Р = 10. ![]()
![]()
![]() Очевидно, что 103
< 3056 < 104 , следовательно, в представлении (1.2) п =
З.
Очевидно, что 103
< 3056 < 104 , следовательно, в представлении (1.2) п =
З.
![]() Разделив интервал [103 ; 104
) на 9 равных частей, получим, что 3•103 S 3056 < 4•10 3
, следовательно, аз = З. У = 3056 - 3,103 = 56 и, так как 10
56 < 10 2 , то = О.
Разделив интервал [103 ; 104
) на 9 равных частей, получим, что 3•103 S 3056 < 4•10 3
, следовательно, аз = З. У = 3056 - 3,103 = 56 и, так как 10
56 < 10 2 , то = О.
![]() Далее получаем 5•10 < 56 < 6•10,
следовательно, ал
Далее получаем 5•10 < 56 < 6•10,
следовательно, ал ![]() Оставшееся число Z = У — 5•10 = 56 — 50 =
6 < 10, следовательно, ао = 6, и построение закончено. В результате
получаем: 3056 = 3•10 3 + 5•10 + 6.
Оставшееся число Z = У — 5•10 = 56 — 50 =
6 < 10, следовательно, ао = 6, и построение закончено. В результате
получаем: 3056 = 3•10 3 + 5•10 + 6.
2) Р = 16.
16 2 3056 < 16 3 , следовательно, в представлении (1.2)
Разделив интервал [162 ; 16 )
на 15 равных частей, получим, что 11•162 3056 < 12•16 2 ,
следовательно, аг = 11. ![]() У = 3056 - 11,16 2 = 240. Но
15•16 S 240 < 16 2 , следовательно, ар 15.
У = 3056 - 11,16 2 = 240. Но
15•16 S 240 < 16 2 , следовательно, ар 15.
И, так как 240 — 15-16 О, то построение окончено,
![]()
В результате получаем: 3056 = 11•16 2 + 15•16.
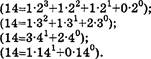 Пример 4.
Десятичное число 14 можно записать в двоичной системе как 11102 (14=12 3 +1
Пример 4.
Десятичное число 14 можно записать в двоичной системе как 11102 (14=12 3 +1
в троичной системе как 1123 в четверичной системе как 324 в 14-ричной системе как 1014
В системах счисления с основанием, ббльшим 14, данное число
будет представлено одной цифрой (это будет буква латинского алфавита Е или
некий другой символ). ![]()
В разделе математики «Теория чисел» доказывается, что и любую правильную дробь можно представить в
виде конечной или бесконечной суммы
отрицательных ![]() степеней любого натурального числа Р >
1. Например:
степеней любого натурального числа Р >
1. Например:
0,123 = 1,10-1 + 210-2 + 3,10-3= + 0,02 + 0,003;
1
![]() = = 1,10-1 + 6,10 -2 + 010 -3 + .
= = 1,10-1 + 6,10 -2 + 010 -3 + . ![]() 6
6
![]() + 0,06 + 0,006 +
+ 0,06 + 0,006 + ![]()
![]() 1415... 1' 10—1 + ф 10 —2 + 1 • 10 —3
+ 5' 10—4 +
1415... 1' 10—1 + ф 10 —2 + 1 • 10 —3
+ 5' 10—4 +![]()
- + 0,04 +
0,001 + 0,0005 + .![]()
![]()
Так как произвольное неотрицательное действительное число можно представить в виде суммы его целой и дробной частей (любая из этих частей может и отсутствовать), то полученные результаты можно обобщить.
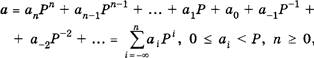 п ? О, (1.5)
п ? О, (1.5)
где Р > 1 — основание позиционной системы счисления, а цифры числа а в Р-ичной системе счисления.
Отрицательные числа в Р-ичных системах счисления представляются с помощью знака «минус» перед выражением вида (1.5) для модуля отрицательного числа. Далее мы будем рассматривать только положительные числа и их представление в Р-ичных системах счисления.
Вопросы и задания
1. Постройте представление десятичного числа Х = 3056 в виде степенного ряда при Р = 2.
2. Покажите, что любое натуральное число может быть
представлено в виде суммы различных неотрицательных степеней числа 2.
З. Во сколько раз увеличится число 3256 , если приписать к нему справа ноль?
4. Как изменится запись Р-ичной дроби с нулевой целой частью, если ее разделить на Р 2 ?
5. Выполните путем рассуждения следующие действия, не используя операцию деления: 100000p:1000p; 201p:100p.
S 1 .З. Представление произвольных чисел в позиционных системах счисления
На основании теоремы 1 мы можем утверждать, что любое число может быть записано в виде суммы степеней числа Р, где Р — натуральное число, большее 1. Вместе с тем, если мы в качестве базиса позиционной системы счисления возьмем возрастающую последовательность степеней числа Р и тем самым однозначно определим Р-ичную систему счисления, то это разложение по степеням числа Р будет являться представлением данного числа в Р-ичной системе счисления.
1.3„1 , Развернутая и свернутая формы записи
Другим способом записи произвольного числа в позиционной системе счисления с основанием Р является последовательное перечисление его значащих цифр, начиная со старшей, при этом целая часть отделяется от дробной запятой. То есть разложению вида (1.5) вещественного числа а по степеням Р соответствует запись вида:
а = а
...чао,а![]()
Представление числа в Р-ичной системе счисления в виде (1.6) называется свернутой формой записи числа.
Таким образом, натуральное число а в Р-ичной системе счисления можно записать двумя равнозначными способами:
а = а Рп + ап 1 рп 1 + + 01 р + а![]() ...чао.
...чао.![]()
Правильную конечную Р-ичную дробь Ь можно записать следующими способами:
-1 -2—К
![]() -1 -2
-1 -2![]()
При использовании развернутой формы для
записи числа в Р-ичной системе счисления основание Р и его степени обычно
записывают в десятичной системе, а цифРЫ — в Р-ичной. При использовании
свернутой формы цифры также записывают в Р-ичной системе, а основа![]() ние Р,
записанное в десятичной системе, приписывают к числу в качестве его нижнего
индекса. Исключение может составлять лишь десятичная система счисления, при
записи чисел в которой индекс часто опускается.
ние Р,
записанное в десятичной системе, приписывают к числу в качестве его нижнего
индекса. Исключение может составлять лишь десятичная система счисления, при
записи чисел в которой индекс часто опускается.
1.3.2. Перечисление натуральных чисел
![]() Вопрос. ПРеДПОЛОЖиМ,
что мы работаем в 50-ричной системе счисления. Можно ли только по свернутой
форме
Вопрос. ПРеДПОЛОЖиМ,
что мы работаем в 50-ричной системе счисления. Можно ли только по свернутой
форме ![]() числа А, не произвоДя никаких вычислений,
опреДелить, больше 50 или нет Десятичный эквивалент ЧИСла А?
числа А, не произвоДя никаких вычислений,
опреДелить, больше 50 или нет Десятичный эквивалент ЧИСла А?
Из ответа на предыдущий вопрос понятно, как в Р-ичной системе счисления перечислять (выписывать в возрастающем порядке) числа, меньшие Р. Само число Р записывается в виде 10р. Для перечисления чисел, больших Р, воспользуемся следующим алгоритмом, описывающим, как по известной Р-ичной форме записи натурального числа ар получить запись следующего натурального числа ар + 1.
Алгоритм перечисления натуральных чисел в Р-ичных системах счисления
1. Если последняя (крайняя справа) цифра числа ар меньше Р — 1, то в следующем по порядку натуральном числе все цифры, кроме последней, будут совпадать с циф-
рами числа ар, а последняя цифра числа ар + 1 будет на единицу больше последней цифры числа ар.
2.
![]() Если последняя цифра числа ар равна Р — 1, то последняя
цифра числа ар + 1 будет равна О, а остальные цифры будут представлять число,
состоящее из первых цифр числа ар (начиная с крайней левой цифры и за
Если последняя цифра числа ар равна Р — 1, то последняя
цифра числа ар + 1 будет равна О, а остальные цифры будут представлять число,
состоящее из первых цифр числа ар (начиная с крайней левой цифры и за![]() канчивая
предпоследней справа), увеличенное на единицу по правилам 1—2 данного
алгоритма; если же первые цифры в записи ар отсутствуют, то число ар + 1 будет
равно 10р.
канчивая
предпоследней справа), увеличенное на единицу по правилам 1—2 данного
алгоритма; если же первые цифры в записи ар отсутствуют, то число ар + 1 будет
равно 10р.
Покажем, как перечислять натуральные числа в различных системах счисления.
Пример 5. В двоичной системе первые 16 чисел будут иметь следующий вид:
|
|
(правило 1); |
|
8 - 10002 |
(трижды примененное правило 2); |
|
9 = 1001 |
(правило 1); |
|
2 |
|
|
10 - 10102 |
(правила |
|
11 - 10112 |
(правило 1); |
|
12 - 11002 |
(дважды примененное правило 2, правило 1); |
|
|
13 -- 11012 |
(правило 1); |
|
|
14 - 11102 |
(правила 2 и 1); |
|
|
15 |
(правило 1); |
|
|
16 = 100002 |
(четырежды примененное правило 2). |
О |
|
|
|
Пример 6. Приведем (без подробных комментариев) некоторые числа в 16-ричной системе счисления:
11
![]() - В16,
- В16, ![]()
12
= ![]()
![]() D 16 , 31 1F16,
D 16 , 31 1F16,
![]() 14
14 ![]() 32
- 2016 ,
32
- 2016 ,
16
15![]()
16 = 1016, 255 - FF16,
16![]() 256 = 10016
256 = 10016![]()
1 .З.З.
Представление ![]() деСЯТИЧНЫХ дробей в Р-ичных системах счисления
деСЯТИЧНЫХ дробей в Р-ичных системах счисления
В общем случае для представления десятичной дроби в Р-ичной системе счисления надо воспользоваться специальными алгоритмами перевода. Однако для некоторых видов десятичных дробей мы можем указать их Р-ичное представление, даже не зная алгоритмов перевода. Речь идет об обыкновенных Дробях. Обыкновенные дроби записываются с помощью отношения числителя и знаменателя, наибольший общий делитель которых равен 1.
В десятичной системе счисления обыкновенная дробь будет точно представима конечной дробью, если существует такое натуральное число т, при умножении на которое знаменателя дроби можно получить некоторую натуральную степень числа 10. Если же такого числа не существует, то эту дробь можно представить только в виде бесконечной периодической дроби.
Ответ. Да, это возможно. Более того, для любой обыкновенной десятичной дроби, не являющейся конечной, можно найти систему счисления, в которой она будет представима конечной дробью. И наоборот, для любой обыкновенной десятичной дроби, являющейся конечной дробью, можно указать систему счисления, в которой она не будет представима конечной дробью.
1 Пример 7. Известно, что правильную
десятичную дробь ![]()
нельзя записать в виде конечной десятичной дроби. Однако в троичной и 9-ричноЙ системах счисления эта дробь будет записана в виде конечной Р-ичной дроби.
1
В 3-ичной системе счисления: = 0,13; З
1
в 9-ричной системе счисления: 0,39 .
з
Общее правило. Десятичная обыкновенная дробь будет точно представима конечной Р-ичной дробью, если существует такое натуральное число т, при умножении на которое знаменателя дроби можно получить некоторую натуральную степень числа Р. Если же такого числа не существует, то в Р-ичной системе счисления дробь окажется бесконечной периодической.
Данный факт следует непосредственно из развернутой формы представления числа.
Кроме того, из развернутого представления дробной части числа следует, что в любой системе счисления с основанием Р верны равенства
1 1 1
![]()
![]() = одр;
= одр; ![]() = 0,0...01
= 0,0...01
Алгоритм записи обыкновенной десятичной дроби в виде конечной Р-ичной дроби
Пусть для нашей дроби существует такое натуральное число т, что при умножении знаменателя на т получаем К-ю степень числа Р.
1. Умножим числитель дроби на т.
2. Представим результат умножения в Р-ичной системе счисления.
З. Дополним числитель, если потребуется, до К цифр нулями слева.
4. Полученное Р-ичное число запишем после запятой. Оно является конечной Р-ичной дробью для исходной обыкновенной.
5
Пример 8. Запишем в двоичной системе. В знаменателе 16 уже стоит четвертая степень двойки. Переведем числитель в двоичную систему (5 = 1012) и дополним получившееся число до четырех цифр: 0101. В результате полу5
чим: = 0,01012.
16
Пример 9. Запишем — в 6-ричной системе. Если знаменатель 18 умножить на 2, то получим 6 2 . Тогда умножим и числи-
зо
![]()
тель на 2. Так как в знаменателе стоит
вторая степень ![]() основания системы счисления, то после
запятой мы дол1
основания системы счисления, то после
запятой мы дол1
жны записать
02. В результате получим: - 0,026. ![]()
18
Вопрос. Можно ли описанный способ преДставления обыкНОоННЫХ Десятичных Дробей в Р-ИЧНЫХ системах счисления использовать для решения обратной заДачи?
Ответ. Так как все Р-ичные системы
равноправны, то описанный способ представления десятичных дробей в Р-ичной
системе счисления можно использовать и для решения обратной задачи:
обыкновенную Р-ичную дробь за![]() писать в десятичной системе счисления, не
производя операции деления числителя на знаменатель.
писать в десятичной системе счисления, не
производя операции деления числителя на знаменатель.
112
Пример 10. Запишем 0,0112 в десятичной системе. 10002
Для того чтобы знаменатель, равный сейчас 2 3 , оказался степенью десяти, его нужно домножить на 5 3 . Таким образом, производя необходимые действия в десятичной системе счисления, получим:
112 з 3-5 3 375
= 0,375.
10002 8 8,53 1000
Вопросы и задания
1. Запишите в развернутом виде числа 657', 10203,405 • 0,15А16; 1AF1H,A920.
2. Какое из чисел больше: 510 или 105', 10002 или 108?
З. Существуют ли системы счисления с основаниями Р и Q, в которых 12p > 21 ?
4. Для десятичного числа 371 найдите основание Р системы счисления, в которой данное число будет представлено теми же цифрами, но записанными в обратном порядке,
т. е. 37110 ![]() 173p.
173p.
5. В каких системах счисления 5p + 5 10 ?
6. В
каких системах счисления 2 р + 2![]()
7. Во сколько раз увеличится число 324 , если справа к нему
![]()
приписать три нуля?
8. Докажите, что в любой позиционной системе счисления с основанием Р > З число 121 р является полным квадратом.
![]()
9. Запишите в 6-ричноЙ системе счисления число, следующее по порядку за числом 5.
10. Какое число следует за числом 111 14 в 14-ричной системе счисления?
11. Какое число предшествует числу 1018 в 18-ричноЙ системе счисления?
12. Выпишите в пятеричной системе счисления все четные числа из диапазона от 1 до 20.
13. Даны числа в
четверичной системе счисления от 1 до 33 ![]() Выпишите все нечетные
числа.
Выпишите все нечетные
числа.
14. Запишите в системе счисления с основанием 234 число 235.
15. Запишите в системе счисления с основанием 240 числа 241, 242, 243, 250, 251.
16. Подсчитайте количество троичных чисел в диапазоне от 123 до 10003.
17. Назовем круглыми все числа, записываемые одной цифрой и несколькими нулями (быть может, одним). Выпишите все двузначные и трехзначные круглые числа в 5-ричной системе счисления.
18. В каких системах счисления 10p является нечетным числом?
19. Как будет выглядеть в двоичной системе счисления десятичное число 0,125?
S 1 .4. Арифметические операции в Р-ичных системах счисления
Во всех позиционных системах счисления арифметические операции выполняются по одним и тем же правилам согласно соответствующим таблицам сложения и умножения. Для всех систем счисления справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный, а также правила сложения, вычитания, умножения и деления столбиком.
1.4.1. Сложение
В Р-ичной системе счисления таблица сложения представляет собой результаты сложения каждой цифры алфавита Р-ичной системы с любой другой цифрой этой же системы. Составить подобную таблицу нетрудно. Наиболее простыми являются таблицы сложения в двоичной и троичной системах счисления (индексы 2 и З опущены).
32
![]()
Таблш.ф1 сложения двоичной и троичной систем счисления
|
|
|
Приведем также таблицу сложения в шестнадцатеричной системе счисления (нижний индекс 16 в обозначении шестнадцатеричных чисел в таблице опущен).
Таблица сложения шестнадцатеричной системы счисления
![]()
|
21 |
2 |
З |
4 |
5 |
1 2 3 4 5 6 7 8 9 6 |
7 |
8 |
9 |
А |
В |
С |
D |
Е |
|
10 11 |
|
2 |
З |
4 |
5 |
6 |
7 |
8 |
9 |
А |
В |
С |
D |
Е |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б
|
6 |
7 |
8 |
9 |
А |
В |
С |
D |
Е |
F |
10 |
11 |
12 |
13 |
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
9 |
А |
в |
с |
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
|
|
А |
в |
с |
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
|
А |
в |
С |
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
19 |
|
|
с |
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
19 |
|
|
с |
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
10 |
11 |
12 |
|
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
Несложно показать, что если результат
сложения двух цифр в Р-ичной системе счисления больше Р — 1 ![]() (т. е.
полученное число двузначное), то старшая цифра результата всегда равна 1.
Действительно, при сложении двух самых старших цифр алфавита мы имеем:
(т. е.
полученное число двузначное), то старшая цифра результата всегда равна 1.
Действительно, при сложении двух самых старших цифр алфавита мы имеем: ![]() 1[Р—2]р.
Например, в четверичной системе счисления: З + З = 12
1[Р—2]р.
Например, в четверичной системе счисления: З + З = 12 ![]()
Следовательно, при сложении столбиком в
любой системе счисления в следующий разряд может переходить только единица, а
результат выполнения сложения в любом разряде будет меньше, чем (максимум ![]() —
1 = 1[Р — 1]р, с учетом переноса единицы из предыдущего разряда). То есть
результат сложения двух поло-
—
1 = 1[Р — 1]р, с учетом переноса единицы из предыдущего разряда). То есть
результат сложения двух поло-
![]()
жительных Р-ичных чисел либо имеет столько же значащих цифр, что и максимальное из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица.
Пример 11. Сложение столбиком в двоичной, троичной и шестнадцатеричной системах счисления.
|
101,012 |
213 |
F2A16 |
|
|
1,112 |
2,13 |
|
|
|
111,002 |
100,13 |
101316 |
2 |
1 .4.2. Вычитание
Вычитание из большего числа меньшего в Р-ичной системе счисления можно производить столбиком аналогично вычитанию в десятичной системе. Для выполнения этой операции будем также использовать таблицу сложения в Р-ичной системе счисления.
Если нам необходимо вычесть из цифры а цифру Ь и а Ь, то в столбце «Ь» таблицы сложения ищем число а. Самая левая цифра в строке, в которой расположено число а, и будет результатом вычитания. Если же а < Ь, то, занимая единицу из левого разряда, мы придем к необходимости выполнения следующего действия: 10p + а — Ь = 1ар — Ь. Для этого в столбце «Ь» таблицы сложения мы уже ищем число 1ар, левая цифра в соответствующей строке является результатом вычитания.
Пример 12. Вычитание в двоичной, троичной и шестнадцатеричной системах счисления.
1012 2103
![]()
10,12 102310216
![]()
10,12 1013 90Е1б
1 .4.3. Умножение
Для выполнения умножения двух многозначных чисел в Р-ичной системе счисления надо иметь таблицы умножения и сложения в этой системе.
Приведем таблицы умножения для двоичной, троичной и шестнадцатеричной систем, опуская нижние ин-
![]()
дексы, указывающие на принадлежность к соответству![]() ющей
системе счисления.
ющей
системе счисления.
Таблщы умножения двоичной и троичной систем счисления

Таблица умножения шестнадцатеричной системы счисления
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
8 |
с |
10 |
14 |
18 |
1C |
20 |
24 |
28 |
2C |
зо |
34 38 |
зс |
|
|
53? |
5 |
А |
|
14 19 |
1Е |
23 |
28 |
2D |
32 |
37 |
ЗС |
41 |
46 |
4В |
|
|
|
6 |
С |
12 |
18 1Е |
24 |
2А |
30 |
36 |
ЗС |
42 |
48 |
4Е |
54 |
5А |
|
|
7+ |
7 |
Е |
15 |
1C |
23 |
2А |
31 |
38 |
ЗР |
46 |
|
54 |
|
62 |
69 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9- |
9 |
12 |
1В |
24 |
2D |
36 |
3F |
48 |
51 |
5А |
63 |
60 |
75 |
7Е |
87 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
С |
18 |
24 |
ЗО |
ЗС |
48 |
54 |
60 |
6C |
78 |
84 |
90 |
эС |
А8 |
|
|
|
D |
1А |
27 |
34 |
41 |
4Е |
5В |
68 |
75 |
82 |
8F |
эС |
А9 |
Вб |
СЗ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() Приведем
примеры выполнения умножения в двоичной, троичной и шестнадцатеричной системах.
Действия производятся по правилам умножения столбиком (последовательное
умножение цифр второго сомножителя на первый сомножитель и сложение
промежуточных результатов), при этом используются соответствующие таблицы
умножения и сложения.
Приведем
примеры выполнения умножения в двоичной, троичной и шестнадцатеричной системах.
Действия производятся по правилам умножения столбиком (последовательное
умножение цифр второго сомножителя на первый сомножитель и сложение
промежуточных результатов), при этом используются соответствующие таблицы
умножения и сложения.
Пример 13. Умножение в различных системах счисления.
101002 Умножение на О не производится. Все
1012 оставшиеся справа нули, не участвующие
![]() 101 в умножении, приписываются справа к ре101 зультату умножения.
101 в умножении, приписываются справа к ре101 зультату умножения.
![]()
11001002![]()
![]()
2123 При сложении столбиком трех и
более слах 12103 гаемых действия сложения целесообразно ![]() 212 производить последовательно, так
как слож1201
212 производить последовательно, так
как слож1201![]() ные вычисления в непривычной системе 12222 счисления могут породить
ошибки.
ные вычисления в непривычной системе 12222 счисления могут породить
ошибки. ![]() 212
212![]()
FFA,316 При умножении Р-ичных дробей количество
|
DFAEA |
ме количеств цифр в дробных частях множи- |
|
CFB4 7 |
телей (если одна или более крайних справа |
|
DDAF,5A16 |
цифр результата окажутся равными нулю, то их можно опустить как незначащие). Ш |
![]()
![]() D,E16 цифр в
дробной части результата равно сум-
D,E16 цифр в
дробной части результата равно сум-
Возможен и другой подход к выполнению арифметических операций. Можно перевести каждый из сомножителей в десятичную систему счисления, произвести требуемое действие в десятичной системе, а результат записать в исходной Р-ичной системе счисления. Аналогичным способом можно поступать и при выполнении операций сложения и вычитания.
1 .4.4. Деление
При делении столбиком в Р-ичной системе счисления приходится в качестве промежуточных вычислений выполнять действия умножения и вычитания, следовательно, используются таблицы умножения и сложения.
Пример 14. Наиболее просто деление организовать в двоичной системе, так как в ней необходимо лишь сравнивать два числа между собой и вычитать из большего числа меньшее.
|
|
|
1102
110
110 ![]()
![]()
Пример 15. Деление столбиком в шестнадцатеричной системе счисления.
36
![]()
|
816 |
|
1Е24,Е1б |
F12716
8
![]()
71
70
12
10
27
20
70
70
Однако результат деления не всегда является конечной Р-ичной дробью (или целым числом). Тогда при осуществлении операции деления обычно требуется выделить непериодическую часть дроби и ее период. Продемонстрируем это на нескольких примерах.
Пример 16. Деление в троичной системе счисления.
|
23 |
|
1,(1)з |
103Так как результат последнего вычитания
-2совпал с предыдущим, то все остальные циф-
10 ры дробной части результата совпадут с по- 2 следней наиденной цифрой. Повторяющаяся 1 цифра образует период троичной дроби.
Деление в двоичной системе счисления.
|
11 |
|
11,0101...2 |
10102В этом примере период
-11 ![]() дроби состоит из двух
дроби состоит из двух
100 цифр. Для определения
-11 периода дроби деление выполняется до тех
![]()
100 пор, пока не будет заметно повторение
- 11 группы цифр в результате. Точнее, должно
100 обнаружиться, что на каком-то этапе вы-
![]() 11 числений результат последнего вычитания
11 числений результат последнего вычитания ![]() 1 совпал с неким предыдущим,
встречавшимся ранее при подсчете именно дробной
1 совпал с неким предыдущим,
встречавшимся ранее при подсчете именно дробной ![]() части. Следовательно, все остальные цифры
дробной части результата будут повторяться такими же группами. Повторяемая
группа и образует период дроби, в данном случае двоичной. 2
части. Следовательно, все остальные цифры
дробной части результата будут повторяться такими же группами. Повторяемая
группа и образует период дроби, в данном случае двоичной. 2
![]()
Вопросы и задания
1. Подсчитайте сумму троичных чисел в диапазоне от 103 до 1003 , включая границы диапазона. Ответ запишите в троичной системе счисления.
2. Найдите сумму шестнадцатеричных чисел:
![]()
Ответ запишите в десятичной системе счисления.
З. Выпишите таблицы сложения и умножения в двенадцатеричной системе счисления.
4. Объясните, почему любая таблица сложения (и умножения) симметрична относительно главной диагонали (линии, проведенной из левого верхнего угла таблицы в ее правый нижний угол).
5. Число, записанное в десятичной системе счисления, оканчивается цифрой 5. Будет ли оно делиться на 5, если его записать в троичной системе счисления?
6. Будут ли справедливы признаки делимости натуральных чисел на 2, З, 5, 9, 10, сформулированные для десятичной системы счисления, и в других системах?
7. В каком случае при прибавлении единицы к числу в Р-ичной системе счисления количество цифр в числе-результате возрастет по сравнению с исходным числом? Может ли количество цифр возрасти больше, чем на одну?
8. Выполните операции сложения и вычитания над следующими парами чисел:
110101012 и 11102; 12345 и 4321$,
ВАВА16 и АВВА16![]()
9. Выполните операцию умножения над следующими парами чисел:
110101012 и 11102; 43215 и 1235;
АВВА12 и 1ОА![]()
10. Выполните операцию деления над следующими парами чисел:
100100002 и 1100$, 43225 и 35; АВО612 и Ап.
11. В следующих примерах найдите пропущенные цифры, обозначенные знаком «*» , определив вначале, в какой системе счисления выполняются действия:
а) 2*21 б) 5*55 в) 21*02 г) 1*01
123* *327 *1212 1**
*203 10100
38
![]()
S 1 .5. Перевод чисел из Р-ичной системы счисления в десятичную
1.5.1. Перевод целых Р-ичных чисел
Дано число в Р-ичной системе счисления а
= а а ...чао. Требуется получить запись этого числа в десятичной системе
счисления. Для решения задачи представим число в развернутой форме: а = а РП
+ ап 1Рп 1 + ... + ч Р + ао (формула (1.7)). Для того чтобы
получить значение этого многочлена в десятичной системе счисления, следует
число Р и коэффициенты при степенях Р (цифры Р-ичного числа) записать в виде
десятичных чисел и все вычисления провести в десятичной системе. Дан![]() ный
способ можно сформулировать в виде следующего алгоритма.
ный
способ можно сформулировать в виде следующего алгоритма.
Алгоритм перевода целых чисел из Р-ичной системы счисления в десятичную
1. Каждая цифра Р-ичного числа переводится в десятичную систему.
2. Полученные числа нумеруются справа налево, начиная с нуля .
З. Число Р переводится в десятичную систему.
4. Десятичное число, соответствующее
каждой Р-ичной цифре, умножается на Р , где К номер этого числа (п. 2),
результаты складываются, причем все арифметические действия проводятся в
десятичной системе. ![]()
Пример 17. Переведем число BOF916 в десятичную систему
счисления.
![]() BOF916
BOF916
=
45 305 ![]() 2
2
При вычислении десятичного значения Р-ичного числа по развернутой форме удобно пользоваться схемой Горнера, которая позволяет получить результат с использованием минимального числа арифметических операций сложения и умножения / деления (операция возведения в степень не используется). Схема Горнера основана на следующих тождественных преобразованиях исходного степенного ряда (многочлена):
![]() + ап_1Р 1 +
+ ап_1Р 1 +
— (а пр п 1 + ап_1РП 2 + +а1)Р+ао —
![]() ((апрп 2 + ап 1Рп З -4- 02)Р + 01)Р + ао —
(1.10) — (((anpn З + ап_1РП 4 + . + аз)Р + 02)Р + + ао
((апрп 2 + ап 1Рп З -4- 02)Р + 01)Р + ао —
(1.10) — (((anpn З + ап_1РП 4 + . + аз)Р + 02)Р + + ао
Пример 18. Применим схему Горнера для
перевода в десятичную систему числа 2143 ![]()
21435 = 2•53 + 1•52 + + З =
![]() ((26
+ + + з = 298
((26
+ + + з = 298 ![]() 2
2
Задание. Подсчитайте, сколько операций сложения и умНОЖеНИЯ потребуется при перевоДе числа BOF916 в де-
сятичную систему «в лоб» и при использовании схемы Горнера.
Для двоичной системы описанный выше алгоритм
перевода чисел из Р-ичной системы в десятичную выгля![]() дит следующим
образом.
дит следующим
образом.
Алгоритм перевода целых чисел из двоичной системы счисления в десятичную
Для того чтобы перевести число из двоичной системы счисления в десятичную, надо в десятичной системе счисления сложить все степени двоек, которые соответствуют единицам в записи исходного двоичного числа. Нумерация степеней ведется справа налево, начиная с нулевой.
Пример 19. Переведем двоичное число 10011012 в деся-
тичное.
10011012 = 20 + 2 2 + 2 3 + 2 6 — 77
![]()
![]() Двоичная система
счисления широко используется в информатике и вычислительной технике, поэтому
очень полезным оказывается знание по крайней мере первых шестнадцати степеней
двойки:
Двоичная система
счисления широко используется в информатике и вычислительной технике, поэтому
очень полезным оказывается знание по крайней мере первых шестнадцати степеней
двойки:
23![]()
24 - 16;
2 5 - 32;
26![]()
2 7 - 128;
28 256;
2 9 - 512;
2 10 = 1024;
2 11 - 2048; 210 32 768; 2 12 - 4096; 2 16 - 65 536.
213 8192;
214
16 384; ![]()
1.5.2. Перевод КОНеЧНЫХ Р-ичных дробей
Дана правильная конечная дробь Ь в Р-ичной системе счисления: Ь = Оф Ь ...Ь_к. Требуется получить запись этой дроби в десятичной системе счисления.
Способ 1
Для решения этой задачи представим аробь в развернутой форме Ь = Ь р- 1 + b_g-2 + ... + Ь_кр- (формула (1.8)). Для того чтобы вычислить значение многочлена в десятичной системе счисления, следует число Р и коэффициенты многочлена (цифры Р-ичного числа) записать в виде десятичных чисел и все вычисления проводить в десятичной системе. Запишем эти правила в виде алгоритма.
Алгоритм перевода конечной Р-ичной дроби в десятичную
1. Целая часть числа переводится в десятичную систему отдельно (см. п. 1.5.1).
2. Каждая цифра дробной части Р-ичного числа переводится в десятичную систему.
4. Число Р переводится в десятичную систему.
5. Десятичное число, соответствующее каждой Р-ичной цифре, умножается на р-к , где К — номер этого числа, результаты складываются, причем все арифметические действия проводятся в десятичной системе.
Пример 20. Переведем число 0,BOF916 в десятичную систему счисления.
0,BOF916 = ![]() = 11,16 -1
= 11,16 -1 ![]()
- 0,691299438476562510![]()
Здесь, согласно пункту З алгоритма, числа были пронумерованы так: 11 — номер один (коэффициент при Р в степени минус один), 15 — номер три, 9 — номер четыре.
При вычислении десятичного значения
Р-ичной дроби по развернутой форме также рекомендуется пользоваться схемой
Горнера, это минимизирует количество необходимых арифметических действий. Для
того чтобы получить схему Горнера для вычисления значения Р-ичной дроби,
выпишем цифры дроби в представлении (1.8) ![]() в обратном порядке:
в обратном порядке:
 -1
-1
-1
(1.11)
-1
Пример 21. Вычислим значение двоичной дроби 0,11012 , используя схему Горнера.
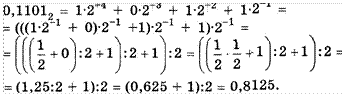 -1
-1
Представим конечную Р-ичную дробь в виде обыкновенной дроби. Числителем этой дроби будет число, стоящее после запятой, а знаменателем -— Р п, где п — количество значащих цифр в дробной части. Знаменатель записывается в десятичной системе. Далее числитель запишем в десятичной системе, и мы получим обыкновенную дробь в десятичной системе. При необходимости ее можно записать в виде десятичной дроби (конечной или периодической, выделяя непериодическую часть и период).
Пример 22. Переведем число 0,1315 в десятичную систему счисления.
![]() 1315 1810 210
1315 1810 210
0,1315 ![]() = 0,0810.
= 0,0810.
15fo 22510 2510
В опрос. В каких случаях целесообразно использовать способ 1, а в каких способ 2?
О твет. Способ 2 наиболее эффективен в случаях, когда среди простых делителей основания системы счисления Р
содержатся какие-нибудь числа, кроме 2 и
5, и соответ![]() ствующую конечную Р-ичную дробь невозможно
представить в виде конечной десятичной дроби.
ствующую конечную Р-ичную дробь невозможно
представить в виде конечной десятичной дроби. ![]()
![]() Пример 23. Переведем число 0,1А15 в десятичную систему
счисления.
Пример 23. Переведем число 0,1А15 в десятичную систему
счисления. ![]() 2510 110
2510 110
о,1А15 ![]()
15io 22510 910 ![]() 2
2
1 .5.3.
Перевод периодических Р-ИЧНЫХ дробей![]()
![]() Существует несколько способов перевода бесконечной
периодической дроби в десятичную систему, причем все они касаются лишь
преобразования периода, а непериодическую дробную часть из Р-ичной системы
счисления в десятичную следует переводить отдельно, используя один из способов
для конечных дробей.
Существует несколько способов перевода бесконечной
периодической дроби в десятичную систему, причем все они касаются лишь
преобразования периода, а непериодическую дробную часть из Р-ичной системы
счисления в десятичную следует переводить отдельно, используя один из способов
для конечных дробей.
Способ 1
Ь = арк =
![]() арр - чат..ак + а.
арр - чат..ак + а.
Отсюда получаем уравнение ар = а + чат..ак, преоб-
разовав его, находим а —![]() В результате для за-
В результате для за-
писи числа а мы получили обыкновенную
дробь. Знаменатель в ней записан в десятичной системе счисления. ![]() Переведя
целое Р-ичное число а1%...ак (числитель) в десятичную систему, мы получим
обыкновенную дробь, записанную в десятичной системе, равную исходному числу а.
При необходимости ее можно перевести в десятичную дробь.
Переведя
целое Р-ичное число а1%...ак (числитель) в десятичную систему, мы получим
обыкновенную дробь, записанную в десятичной системе, равную исходному числу а.
При необходимости ее можно перевести в десятичную дробь.
![]() Пример 24. Пусть а = тогда
Пример 24. Пусть а = тогда
Ь = 2 4
•а = а + 1001 ![]()
Мы получаем уравнение 16•а = а + 9, из которого находим: а ![]() =
0,610.
=
0,610.
15 5
![]() При наличии
непериодической части вычисления изменятся незначительно. Пусть периодическая
Р-ичная дробь имеет вид: Ь = Обозначим через а следующую дробь: а = Тогда
исходную дробь можно выразить через а так: Ь = р-па + 0,c1c2
При наличии
непериодической части вычисления изменятся незначительно. Пусть периодическая
Р-ичная дробь имеет вид: Ь = Обозначим через а следующую дробь: а = Тогда
исходную дробь можно выразить через а так: Ь = р-па + 0,c1c2 ![]() (сдвигаем
период на п Р-ичных разрядов вправо и прибавляем непериодическую часть). Далее
переводим отдельно в десятичную систему конечную дробь 0,c1c2
(сдвигаем
период на п Р-ичных разрядов вправо и прибавляем непериодическую часть). Далее
переводим отдельно в десятичную систему конечную дробь 0,c1c2 ![]() чисто
периодическую дробь а =
чисто
периодическую дробь а =
Пример 25. = + 0,12
= 24 0,610 + 0,12 = +
0,510 - 0,6510 ![]() 2-2-0,610 = 0,15
2-2-0,610 = 0,15![]()
Непериодическая часть последней двоичной дроби состоит из двух нулей, но ее нельзя считать отсутствующей, так как она определяет сдвиг периода.
Способ 2
Запишем исходную бесконечную периодическую дробь в виде следующей бесконечной суммы:
![]()
За исключением непериодической части данное выражение соответствует сумме бесконечной геометрической прог_рессии со знаменателем q = р-к < 1 и первым членом
![]() • чат..ак. Как известно, сумма такой
прогрессии конечна и равна:
• чат..ак. Как известно, сумма такой
прогрессии конечна и равна:
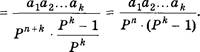 Р п К • ар2...ак
Р п К • ар2...ак
—К
Остается лишь записать числитель и знаменатель полученного отношения в десятичной системе счисления и прибавить к результату непериодическую часть дроби, предварительно переведенную в десятичную систему.
Пример 26. Переведем двоичную периодическую дробь ![]() в
десятичную. Для этого представим исходную дробь в виде:
в
десятичную. Для этого представим исходную дробь в виде:
![]() = 0,12 + 2-6,10012 + 2 10 ,10012 + 2 14 ,10012 +...
= 0,12 + 2-6,10012 + 2 10 ,10012 + 2 14 ,10012 +...
Легко увидеть, что слагаемые этой бесконечной суммы, начиная со второго, представляют собой бесконечную геометрическую прогрессию со знаменателем q = 2 и первым членом Ь = 2 -6 •10012. Сумма этой бесконечной 2-6.10012 геометрической прогрессии равна Переведем 1 - 2 4
числитель пол енной величины в десятичную систему
счисления: 2- • 10012 ![]() 2 + 1) = 2 -6 ,9.
2 + 1) = 2 -6 ,9.
9 9
Тогда![]() = 0,12
= 0,12 ![]() = 0,5 +
= 0,5 + ![]() - 0,6510.
- 0,6510.
4 .(2 4 -1) 4 -15
Вопросы и задания
1. Переведите в десятичную систему счисления двоичные числа:
1', 1012; 100002; 10001010102; 11001011![]()
2. Переведите в десятичную систему счисления числа, записанные в пятеричной системе счисления: 15; 3015; 1212345.
4. Переведите
следующие числа в десятичную систему счисления.• 1234; 123,45; 203,56;![]()
5. Подсчитайте количество используемых операций (сложения и умножения) при вычислении десятичного значения числа ABCDA916 по развернутой форме записи и по схеме Горнера. Вместо операции возведения в степень используются несколько операций умножения.
6. Дано действительное число х. Дайте словесную запись алгоритма, позволяющего не более чем за четыре умножения и четыре сложения вычислить значение следующего выражения: 2х4 + 3х3 + 4х2 + 5х + 6.
S 1 .б, Перевод чисел из десятичной
системы счисления в Р-ичную ![]()
1.6.1. два способа перевода целых чисел
Способ 1. Перевод делением на Р с остатком.
Запишем число а в Р-ичной системе счисления в развернутой форме (1.7):
![]()
где а , а ... Ч, ао пока неизвестны. Тогда, разделив а на Р с остатком, получаем целое частное: п—1 п—2
![]() (1.12)
(1.12)
1 и ао в остатке, не превышающее Р — 1. Таким образом, мы
определили последнюю цифру в Р-ичной записи числа а. Разделив полученное
частное (1.12) вновь на Р, получим в остатке значение Ч. Новое частное: а Р п
2 + ![]() п—1 + 02. Таким образом, мы определили
предпоследнюю цифру в Р-ичной записи числа а. Продолэкаем этот процесс, пока
частное при целочисленном делении не станет равным нулю. Более формально данный
способ можно записать в виде следухощего алгоритма.
п—1 + 02. Таким образом, мы определили
предпоследнюю цифру в Р-ичной записи числа а. Продолэкаем этот процесс, пока
частное при целочисленном делении не станет равным нулю. Более формально данный
способ можно записать в виде следухощего алгоритма.
Алгоритм перевода целого числа из десятичной системы счисления в Р-ичную
1.
2. Остаток от деления заменяем на соответствующую цифру в Р-ичной системе счисления и приписываем ее слева к полученным ранее цифрам Р-ичной записи числа а (первая полученная цифра соответствует младшему разряду).
З. Выполняем пункты 1 и 2, до тех пор пока число а не станет равным О,
Пример 27. Переведем число 123 в троичную систему счисления.
|
123. 41 |
(0) |
В скобках указаны остатки от цело- |
|
41.в = 13 |
(2) |
численного деления, которые явля- |
|
13:3 - |
(1) |
ются соответствующими цифрами в |
|
4:3 = 1 |
(1) |
троичном представлении числа. |
Ответ: 123 = 111203.
Переведем это же число в шестнадцатеричную систему счисления.
![]() 123:16
= 7
123:16
= 7![]()
![]() (7)
(7)
Заменим число 11 на шестнадцатеричную цифру В. Ответ: 123 =
7В ![]()
Способ 2. Этот способ основан на выделении максимальной степени числа Р в исходном десятичном числе.
Заменим в развернутой форме записи числа в Р-ичной системе все цифры на максимальную (равную Р—1) и покажем, что и в этом случае число строго меньше, чем Р+1 . Очевидно, что такое число также не меньше, чем Р, так как а > 1.
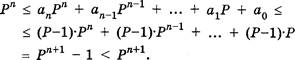 + (Р-1)
+ (Р-1)![]()
Последнее равенство получено с использованием формулы суммы конечного числа членов геометрической прогрессии .
РК ап_1РП 1 + + + S рп .
Тогда п — 1 — К следующих за ап цифр будут равны нулю (при п — 1 = К нулевые цифры между ап и ак отсутствуют), а ак получаем в результате деления нацело а на РК . Пока остаток от такого деления не окажется равен нулю, будем продолжать описанные действия.
Задание. Запишите описанный способ 6 виде алгоритма.
Пример 28. Переведем вторым способом число 100 в двоичную систему счисления.
Используя таблицу степеней двойки, запишем неравенства: 2 6 < 100 < 2 7 . Следовательно, двоичная запись числа 100 будет состоять из 7 цифр. Целая часть от деления 100 на 2 6 равна 1, т. е, старшая цифра искомого числа равна 1. Остаток от деления 100 на 2 6 равен 36. Так как 2 5 < 36 < 2 6 , то и вторая слева цифра равна единице. Остаток же от деления 36 на 2 5 равен 4 = 2 2 , т. е. третья и четвертая, а также шестая и седьмая цифры в двоичной записи числа 100 нулевые. Ответ: 10010 = 11001002.
Пример 29. Переведем в шестнадцатеричную систему счисления число 525.
Заметим, что второй способ перевода
эффективен лишь тогда, когда нам уже известны значения всех степеней числа Р,
которые не превосходят исходное число. Но преимущество такого метода состоит в
естественном порядке записи получившихся Р-ичных цифр (слева направо), что
бывает важно при программировании: очередная полученная цифра сразу же может
выводиться на печать. В первом же способе перевода все цифры надо
предварительно запомнить для последующей распечатки ![]() результата в порядке,
обратном их получению.
результата в порядке,
обратном их получению.
1.6.2, Перевод конечных десятичных дробей
В этом разделе мы рассмотрим перевод только конечных десятичных дробей.
Если в дроби есть ненулевая целая часть, то она переводится из десятичной системы в Р-ичную отдельно. Сформулируем правила перевода дробной части.
![]() Дана правильная конечная десятичная дробь
Ь. Допу
Дана правильная конечная десятичная дробь
Ь. Допу![]() стим, что в Р-ичной системе наша дробь Ь
имеет вид
стим, что в Р-ичной системе наша дробь Ь
имеет вид ![]() = 0 ' b -1 -2 к (в
Р-ичной системе дробь может оказаться и бесконечной). Необходимо найти цифры Ь
= 0 ' b -1 -2 к (в
Р-ичной системе дробь может оказаться и бесконечной). Необходимо найти цифры Ь![]()
![]()
Запишем десятичную дробь Ь в развернутой форме в
Р-ичной системе счисления:
-1 -2-к
![]() -1 -2
-1 -2 ![]() —К
—К ![]() (1.13)
Умножим левую (само число) и правую части выражения (1.13) на Р. В правой части
получим:
(1.13)
Умножим левую (само число) и правую части выражения (1.13) на Р. В правой части
получим:
![]() -1
-1
-1 -2 -к (1.14)
![]()
значит, первая цифра Ь_1 дробной части числа Ь в Р-ичной
системе равна целой части результата умножения десятичной дроби Ь на Р. Дробную
часть результата умножения обозначим через Ь, т. е. Ь = b_y-1 + + Ь_ р-К+1 +![]()
Сформулируем описанные выше правила перевода десятичных дробей в Р-ичную систему в виде алгоритма.
Алгоритм перевода правильной конечной десятичной дроби в Р-ичную систему счисления
1. Умножим исходное число на Р (основание системы счисления), целая часть полученного произведения является первой цифрой после запятой в искомом числе.
2. Если дробная часть произведения не равна О, умножим ее на Р, целую часть полученного числа заменим на цифру в Р-ичной системе и припишем ее справа к результату.
З. Выполняем пункт 2 до тех пор, пока дробная часть произведения не станет равной нулю или не выделится период (дробная часть окажется равной уже получавшейся ранее дробной части произведения).
Пример 30. Переведем число 0,375 в двоичную систему.
0,75 о — первая цифра результата
0,75 1 — вторая цифра результата
0,5последняя цифра результата ответ: 0,375 = 0,0112.
![]() Переведем число
0,515625 в четверичную систему. 2,0625 2
Переведем число
0,515625 в четверичную систему. 2,0625 2
1 ![]() ответ: 0,515625 =
0,201
ответ: 0,515625 =
0,201 ![]()
Переведем число О, 109375 в шестнадцатеричную систему.
1,75 1
![]() - 12,0 1210
- 12,0 1210 ![]() ответ:
0,109375 = о,1С16
ответ:
0,109375 = о,1С16![]()
Пример 31. Переведем число 0,123 в пятеричную систему.
![]() 0,1236 = 0,615
0,1236 = 0,615
0,6156 3,075
![]() 0,0756 = 0,375
0,0756 = 0,375
0,8756 = 4,375
![]() Дробная часть
последнего произведения равна уже встречавшейся ранее дробной части,
следовательно, последние две цифры образуют период пятеричной дроби.
Дробная часть
последнего произведения равна уже встречавшейся ранее дробной части,
следовательно, последние две цифры образуют период пятеричной дроби.
ответ: 0,123 =![]()
Задание. Докажите, что при переводе конечных ДесятичНЫХ Дробей в Р-ичнџю систему счисления можно получить или конечную Р-ичную дробь, или периоДическую дробь (бесконечную непериоДическую дробь получить нельзя).
Вопросы и задания
1. Переведите десятичное число 52 в двоичную, восьмеричную и 11-ричную системы счисления.
2. Переведите число 2005 в систему счисления с основанием, равным вашему возрасту. Может ли в новой системе счисления получившееся число быть дробным?
З. Переведите следующие десятичные дроби в троичную и восьмеричную системы счисления: 0,1; 0,3; 0,8.
4. Требуется выбрать 5 различных гирь так, чтобы с их помощью можно было взвесить любой груз до 30 кг включительно при условии, что гири ставятся только на одну чашу весов. (Эта задача приведена в книге Л. Фибоначчи. Ею также интересовался Л. Эйлер.)
5. Переведите в
восьмеричную систему счисления конечную шестнадцатеричную дробь BF3,616![]()
6. Найдите 1999-ю
цифру после запятой в четверичной записи десятичного числа 20,45.![]()
S 1 .7, Смешанные системы счисления
![]() В некоторых случаях
числа, заданные в системе счисления с основанием Q, приходится изображать с
помощью цифр другой Р-ичной системы счисления.
В некоторых случаях
числа, заданные в системе счисления с основанием Q, приходится изображать с
помощью цифр другой Р-ичной системы счисления.
![]()
Например, ранее широкое распространение в вычислительной технике имела двоично-десятичная система. В двоично-десятичной системе счисления основанием системы счисления является число 10, но все десятичные цифры отдельно кодируются четырьмя двоичными цифрами и в таком виде записываются последовательно друг за другом. Так, число 83910 в двоично-десятичной системе счисления будет записываться как 1000001110012 . Заметим, что такое представление обладает избыточностью, поскольку четыре двоичные цифры могут кодировать не 10, а 16 различных чисел.
Особый интерес представляет случай, когда
Q = Рт где т — натуральное число. Для таких систем вид числа ![]() в Р—фичной
системе совпадает с видом числа в Р-ичной системе. Тогда перевод чисел из
Р-ичной системы счисления в фичную и наоборот может производиться по более
простым алгоритмам (сформулируем и докажем их пока только для целых чисел).
в Р—фичной
системе совпадает с видом числа в Р-ичной системе. Тогда перевод чисел из
Р-ичной системы счисления в фичную и наоборот может производиться по более
простым алгоритмам (сформулируем и докажем их пока только для целых чисел).
Теорема 2. Для того чтобы перевести целое число из системы счисления- с основанием Р в систему счисления с основанием Q = Р Т , где т — натуральное число, достаточно запись числа в Р-ичной системе разбить на группы по т цифр, начиная с правой цифры, и каждую такую группу заменить одной цифрой в фичной системе.
Например: 101012 101101
= 8![]()
Доказательство. Запишем исходное число в развернутом виде в системах счисления с основаниями Р и Q:
2 о ![]()
![]()
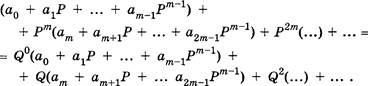
Покажем, что любой многочлен в скобках строго меньше Q. Для этого каждую цифру Р-ичной системы счисления а. заменим на максимальную цифру [Р—1] алфавита этой системы:
![]() ао + 01Р + ... + ат_1РТ 1
(Р— + р + р2 +
ао + 01Р + ... + ат_1РТ 1
(Р— + р + р2 +![]()
Р Т -1
![]()
Р-1
В приведенных преобразованиях была применена формула суммы конечного числа элементов геометрической прогрессии со знаменателем Р и первым членом, равным единице.
Следовательно, каждый многочлен в
скобках при сте![]() пенях Q можно записать в виде одной цифры
фичной системы счисления. В силу единственности представления натуральных чисел
в любой системе счисления:
пенях Q можно записать в виде одной цифры
фичной системы счисления. В силу единственности представления натуральных чисел
в любой системе счисления:
![]()
Теорема Доказана.
Теорема З. Для того чтобы перевести целое число из системы счисления с основанием Q = РТ , где т — натуральное число, в систему счисления с основанием Р, необходимо каждую ф•ичную цифру перевести в систему с основанием Р и дополнить, если это необходимо, полученные числа слева нулями так, чтобы каждое число, за исключением самого левого, состояло ровно из т цифр.
Например:
7316 ![]() 111011
= 11100112 (Р = 2; 16; т = 4).
111011
= 11100112 (Р = 2; 16; т = 4).
Доказательство. Представим каждую цифру
bi, i = О, ![]() (формула (1.15)) в представлении исходного
числа в Фичной системе счисления в Р-ичной системе счисления. Так как Ь. < Q
= = РТ , то максимальное количество цифр в полученном представлении
равно т.
(формула (1.15)) в представлении исходного
числа в Фичной системе счисления в Р-ичной системе счисления. Так как Ь. < Q
= = РТ , то максимальное количество цифр в полученном представлении
равно т.
2
![]()
![]() 01 02 0(т-1)
01 02 0(т-1)
+ рте 10 + 611 р + ь 12р 2 + +
1(m—1)![]()
![]() а ; = ар
а ; = ар![]()
Теорема Доказана.
Примечание. Аналогичные утверждения справедливы также и для правильных дробей. Перевод дробной части из фичной системы в Р-ичную осуществляется, как и для целых чисел. Незначащими в дробной части теперь являются правые нули в Р-ичном представлении самой правой цифры дробной части Фичного числа. При обратном же переводе цифры Р-ичной дроби группируются по т ШТУК слева направо, начиная с первой цифры после запятой. Если последняя группа содержит менее т цифр, то к ней добавляют справа соответствующее количество нулей.
Пример 32. Переведем двоичное число 1010,000110112 в восьмеричную систему счисления.
![]() Для двоичной и
восьмеричной систем счисления выполняется соотношение Q = Р Т , а
именно 8 = 2 3 . Следовательно, при переводе будем группировать
цифры двоичного числа по три (в целой части справа налево, в
Для двоичной и
восьмеричной систем счисления выполняется соотношение Q = Р Т , а
именно 8 = 2 3 . Следовательно, при переводе будем группировать
цифры двоичного числа по три (в целой части справа налево, в
дробной части слева направо): 1l010,l0001110l112 ![]() -
12,0668 (последняя группа двоичных цифр была дополнена нулем справа).
-
12,0668 (последняя группа двоичных цифр была дополнена нулем справа).
ответ: 1010,000110112 = 12,0668.
Пример 33. Переведем число А, 1016 из шестнадцатеричной системы счисления в четверичную.
Для шестнадцатеричной и четверичной
систем счисления ![]() выполняется соотношение Q = РТ ,
а именно 16 = 4 2 . Поэтому заменим каждую 16-ричную цифру ее
4-ричным представлением, для чего используем десятичную систему в качестве
промежуточной: А 16 = 1010 224; с16
выполняется соотношение Q = РТ ,
а именно 16 = 4 2 . Поэтому заменим каждую 16-ричную цифру ее
4-ричным представлением, для чего используем десятичную систему в качестве
промежуточной: А 16 = 1010 224; с16 ![]() = 1210 = 304. Тогда А,1С16 22,l01l304
(последний незначащий О можно опустить). Ответ: АДС16 = 22,0134.
= 1210 = 304. Тогда А,1С16 22,l01l304
(последний незначащий О можно опустить). Ответ: АДС16 = 22,0134.
Полученные результаты для смешанных систем счисления, таких что РТ = Q, имеют ряд практических применений.
1.
2. Замена системы счисления с меньшим основанием Р на систему с ббльшим основанием Q = Р Т обеспечивает сокращение записи числа, уменьшая количество цифр в т раз. Например, при использовании двоичной системы счисления числа можно представлять в 16-ричной, сократив количество цифр в записи числа в 4 раза (16 = 2 4 ).
З. В некоторых случаях удается сделать более рациональным решение задачи перевода чисел из одной системыв другую, даже если непосредственно их основания не связаны соотношением Q = Р Т . Например, при переводе чисел из восьмеричной системы в шестнадцатеричную и наоборот удобно сначала переписать число в двоичном виде (8 = 2 3 и 24 - 16).
Пример 34. Переведем
число BF3,616 в восьмеричную систе![]() му счисления:
му счисления:
![]() = 5763,38.
= 5763,38.
Вопросы и задания
1. Переведите десятичные числа а = 645, Ь = 383 в двоичную, восьмеричную и шестнадцатеричную системы счисления и заполните следующую таблицу:
|
Выражение |
Система счисления |
|||
|
10-тичная |
16-ричная |
8-ричная |
2-ичная |
|
|
а |
645 |
|
|
|
|
|
383 |
|
|
|
|
|
|
|
|
|
2. Переведите число 1234,56789 в 27-ричную систему счисления, а число ABCD,EF16 — в восьмеричную.
4. Во сколько раз сократится количество цифр в записи числа, если его перевести из четверичной системы счисления в 64-ричную? А из десятичной в 10 ООО-ричную?
5. Выпишите четверичные представления для всех цифр алфавита шестнадцатеричной системы счисления и переведите число 12345678,9ABCDEF16 в четверичную систему, не используя его двоичное представление в качестве промежуточного.
S 1 .8. Системы счисления и архитектура компьютеров
В каждой области науки и техники существуют фундаментальные идеи или принципы, которые определяют ее содержание и развитие. В компьютерной науке роль таких фундаментальных идей сыграли принципы, сформулированные независимо друг от друга двумя крупнейшими учеными ХХ века — американским математиком и физиком Джоном фон Нейманом и советским инженером и ученым Сергеем -4- Александровичем Лебедевым.
Центральное место среди «принципов Неймана—Лебедева» , определяющих архитектуру ЭВМ, занимает предложение об использоваДж. фон нии двоичной системы счисления. Это предло-
Нейман жение было обусловлено рядом обстоятельств:
 (1903-1957) простотой
выполнения арифметических операций в двоичной системе счисления; ее
«оптимальным» согласованием с булевой логикой; простотой технической реализации
двоичного элемента памяти (триггера).
(1903-1957) простотой
выполнения арифметических операций в двоичной системе счисления; ее
«оптимальным» согласованием с булевой логикой; простотой технической реализации
двоичного элемента памяти (триггера).
Однако на определенном этапе развития компьютерной техники было выявлено, что использование классической двоичной систе-
С. А. Лебедев мы счисления для представления информа(1902—1974) ции в компьютере имеет существенные недостажи. Первым из них является так называемая проблема представления отрицательных чисел. Второй недостаток двоичной системы счисления получил название нулевой избыточности.
Как известно, отрицательные числа непосредственно не могут быть представлены в двоичной системе счисления, использующей только две цифры 0 и 1. Перед модулем отрицательного числа необходимо ставить знак «минус». Это влечет за собой необходимость анализировать знаки операндов при выполнении арифметических операций, что снижает скорость обработки информации. Для того чтобы не выполнять анализ операндов, был разработан и реализован способ представления целых отрицательных чисел в виде дополнительного кода (см. главу 2), что существенно упростило схему выполнения арифметических операций, но затруднило восприятие записи отрицательных чисел.
Второй недостаток двоичной системы особенно неприятен
при хранении и передаче двоичных кодов. Нулевая избыточность (т. е. отсутствие
избыточности) двоичного представления означает, что в системе счисления
отсутствует механизм обнаружения ошибок, которые, к сожалению, неизбежно
возникают в компьютерных системах под ![]() влиянием внешних и внутренних
факторов.
влиянием внешних и внутренних
факторов.
![]() Суть этой проблемы
состоит в следующем. Пусть в процессе передачи или хранения информации,
представленной, например, двоичным кодом 10011010, под влиянием внешних или
внутренних факторов произошло искажение информации, и она перешла в кодовую
комбинацию 11010010 (искаженные разряды подчеркнуты). Поскольку комбинация
11010010 (как и любой другой двоичный код) является «разрешенной» в двоичной
системе счисления, то без дополнительных действий невозможно определить,
произошло искажение информации или нет. Для решения этой проблемы можно,
например, для каждого байта (8 разрядов двоичного числа) подсчитывать
количество единиц, или для группы байтов подсчитывать контрольную сумму и т. д.
В любом случае должны быть использованы специальные методы избыточного кодирования,
что замедляет работу компьютера и требует дополнительной памяти.
Суть этой проблемы
состоит в следующем. Пусть в процессе передачи или хранения информации,
представленной, например, двоичным кодом 10011010, под влиянием внешних или
внутренних факторов произошло искажение информации, и она перешла в кодовую
комбинацию 11010010 (искаженные разряды подчеркнуты). Поскольку комбинация
11010010 (как и любой другой двоичный код) является «разрешенной» в двоичной
системе счисления, то без дополнительных действий невозможно определить,
произошло искажение информации или нет. Для решения этой проблемы можно,
например, для каждого байта (8 разрядов двоичного числа) подсчитывать
количество единиц, или для группы байтов подсчитывать контрольную сумму и т. д.
В любом случае должны быть использованы специальные методы избыточного кодирования,
что замедляет работу компьютера и требует дополнительной памяти.
Попытка преодолеть эти и другие недостатки двоичной системы счисления стимулировала использование в компьютерах других систем счисления и развитие собственно теории систем счисления.
1 ,8.1 . Использование уравновешенной троичной системы счисления
Для преодоления недостатков использования двоичной системы для кодирования информации уже на этапе зарождения компьютерной эры был выполнен ряд проектов и сделано несколько интересных математических открытий, связанных с системами счисления. Пожалуй, наиболее интересным проектом в этом отношении является троичный компьютер «Сетунь», разработанный в 1958 г. в Московском государственном университете им. М. В. Ломоносова иод руководством Н. П. Брусенцова (Сетунь — название речки, протекающей неподалеку от МГУ).
В ЭВМ «Сетунь» применялась
уравновешенная (симметричная) троичная система счисления для представления
чисел, использование которой впервые в истории компьютеров поставило знак
равенства между представлением отЭВМ «Сетунь» рицательных и положительных
чисел, позволило отказаться от различных «ухищрений», используемых для
представления отрицательных чисел. Это обстоятельство, а также использование
«троичной логики» при разработке программного обеспечения привело к созданию
весьма совер![]() шенной архитектуры компьютера.
шенной архитектуры компьютера.
ЭВМ «Сетунь» является наиболее ярким примером,
![]() подтверждающим
влияние системы счисления на архитектуру компьютера!
подтверждающим
влияние системы счисления на архитектуру компьютера! ![]()
Определение 9. Система счисления с основанием Р = З и цифрами 1, О, 1, где 1 означает «минус единица», называется уравновешенной троичной или симметричной троичной системой счисления.
Пример 35. Приведем примеры записи некоторых чисел в уравновешенной троичной системе:
|
Положитель- ные десятичные числа |
Положительные троичные уравновешенные числа |
Отрицательные троичные уравновешенные числа |
Отрицатель- ные десятичные числа |
|
1 |
1 |
|
-1 |
|
2 |
1 1 |
i 1 |
-2 |
|
з |
|
1 0 |
-3 |
|
4 |
1 1 |
1 i |
—4 |
|
5 |
1 1 i |
1 1 1 |
-5 |
|
6 |
1 1 0 |
1 1 0 |
—6 |
|
7 |
1 1 1 |
1 |
|
|
8 |
1 0 1 |
1 0 1 |
-8 |
|
9 |
1 0 0 |
1 0 0 |
—9 |
|
10 |
1 0 1 |
1 0 1 |
-10 |
|
11 |
1 1 1 |
1 |
-11 |
|
12 |
1 1 0 |
1 1 0 |
-12 |
|
13 |
1 1 1 |
1 1 1 |
-13 |
|
14 |
|
|
— 14 |
Из приведенного примера понятно, почему
эта систе![]() ма счисления называется уравновешенной или
симметричной.
ма счисления называется уравновешенной или
симметричной.
Главная особенность уравновешенных систем счисления — при выполнении арифметических операций не используется «правило знаков» .
1 .8.2.
Использование Фибоначчиевой системы ![]() счисления
счисления
На заре компьютерной эры было сделано
еще два открытия в области позиционных способов представления чисел, которые,
однако, малоизвестны и в тот период не привлекли особого внимания математиков и
инженеров. ![]() Речь идет о свойствах Фибоначчиевой
системы счисления и системы счисления золотой пропорции.
Речь идет о свойствах Фибоначчиевой
системы счисления и системы счисления золотой пропорции.
![]() Основное преимущество кодов Фибоначчи для
практических применений состоит в их «естественной» избыточности, которая может
быть использована для целей контроля числовых преобразований. Эта избыточность
проявляет себя в свойстве множественности представлений одного и того же числа.
Например, число 30 в коде Фибоначчи имеет несколько представлений:
Основное преимущество кодов Фибоначчи для
практических применений состоит в их «естественной» избыточности, которая может
быть использована для целей контроля числовых преобразований. Эта избыточность
проявляет себя в свойстве множественности представлений одного и того же числа.
Например, число 30 в коде Фибоначчи имеет несколько представлений:
зо = 1001101 1010001 ![]() fib fibfib'
fib fibfib'
При этом различные кодовые
представления одного и того же числа могут быть получены друг из друга с
помощью специальных Фибоначчиевых операций свертки (011 -» 100) и развертки
(100 -» 011), выполняемых над кодовым изображением числа. Если над кодовым изоб![]() ражением
выполнить все возможные свертки, то мы придем к специальному Фибоначчиевому
изображению, называемому минимальной формой, в которой нет двух рядом стоящих
единиц. Если же в кодовом изображении выполнить все возможные операции
развертки, то придем к специальному Фибоначчиевому изображению, называемому
максимальной или развернутой формой, в которой рядом не встречаются два нуля.
ражением
выполнить все возможные свертки, то мы придем к специальному Фибоначчиевому
изображению, называемому минимальной формой, в которой нет двух рядом стоящих
единиц. Если же в кодовом изображении выполнить все возможные операции
развертки, то придем к специальному Фибоначчиевому изображению, называемому
максимальной или развернутой формой, в которой рядом не встречаются два нуля.
Анализ Фибоначчиевой арифметики показал, что основными ее операциями являются операции свертки, развертки и основанная на них операция приведения кода Фибоначчи к минимальной форме.
Эти математические результаты стали основой для проекта создания компьютерных и измерительных систем на основе Фибоначчиевой системы счисления.
![]() Отличительной
особенностью микросхемы являлось наличие контрольного выхода, на котором
формировалась информация о неправильной работе микросхемы.
Отличительной
особенностью микросхемы являлось наличие контрольного выхода, на котором
формировалась информация о неправильной работе микросхемы.
Таким образом, основным результатом
этой разработки было создание первой в истории компьютерной техники микросхемы
для реализации самоконтролирующе![]() гося Фибоначчи-процессора со
стопроцентной гарантией обнаружения сбоев, возникающих при переключении
триггеров.
гося Фибоначчи-процессора со
стопроцентной гарантией обнаружения сбоев, возникающих при переключении
триггеров.
![]() И хотя создать
Фибоначчи-компьютер по разным причинам пока так и не удалось, теоретические
основы дан
И хотя создать
Фибоначчи-компьютер по разным причинам пока так и не удалось, теоретические
основы дан![]() ного направления представляют несомненный
интерес и могут стать источником новых идей не только в компьютерной области,
но и в области математики. Особенно эффективным считается использование
«Фибоначчие
ного направления представляют несомненный
интерес и могут стать источником новых идей не только в компьютерной области,
но и в области математики. Особенно эффективным считается использование
«Фибоначчие![]() вых» представлений в измерительной
технике и цифровой обработке сигналов.
вых» представлений в измерительной
технике и цифровой обработке сигналов.
1.8.3. Недвоичные компьютерные арифметики
При разработке вычислительной техники
перед математиками всегда стоит сложнейшая проблема — создание эффективных (их
часто называют «предельными») алгоритмов выполнения арифметических операций в
компьютере. В рамках решения этой проблемы учеными были придуманы новые системы
счисления и разработаны компьютерные арифметики на их основе, которые позволяют
построить вычислительные устройства, быстродействие и надежность которых
превосходят вычислители, основанные на двоичной арифметике. К таким системам
счисления можно отнести непозиционную систему остаточных классов, некоторые
иерархические системы счис![]() ления и др.
ления и др.
Система остаточных классов (СОК) — это непозиционная система счисления, числа в которой представляются остатками от деления на выбранную систему оснований Р 1 , Р 2 , Р и являются взаимно простыми числами. Операции сложения, вычитания и умножения над числами в СОК производятся независимо по каждому основанию без переносов между разрядами.
Такие операции, как деление, сравнение и др., требующие информации о величине всего числа, в СОК выполняются по более сложным алгоритмам. И в этом заключается существенный недостаток данной системы счисления, сдерживающий ее широкое применение в качестве компьютерной. Однако сегодня в современных компьютерах при работе с большими и супербольшими числами используют СОК, ибо только СОК-арифметика позволяет получать результаты вычислений в реальном времени.
В таких случаях в качестве оснований СОК берут величины,
близкие к 2т 171(т — двоичная т разрядность компьютера),
например, 2 ![]() 2 - + 1 и т. д. Начиная с середины
прошлого столетия ученые многих стран мира, включая и нашу, занимаются
проблемой повышения скорости «неудобных» операций в СОК. Сама же система
остаточных классов применяется в вычислительных системах достаточно широко уже
несколько десятилетий.
2 - + 1 и т. д. Начиная с середины
прошлого столетия ученые многих стран мира, включая и нашу, занимаются
проблемой повышения скорости «неудобных» операций в СОК. Сама же система
остаточных классов применяется в вычислительных системах достаточно широко уже
несколько десятилетий.
Вопросы и задания ![]()
1. Перечислите первые 14 натуральных чисел в Фибоначчиевой системе счисления в минимальной форме.
2. Сформулируйте правила перечисления натуральных чисел в Фибоначчиевой системе.
З. Сформулируйте правила перечисления натуральных чисел в троичной уравновешенной системе счисления.
4. Сформулируйте правила сложения в Фибоначчиевой системе счисления.
5.
6. Объясните, почему системы счисления, аналогичные используемой в ЭВМ «Сетунь», называют уравновешенными или симметричными.
7. Напишите алгоритм составления таблицы сложения в Р-ичной системе счисления.
8. Напишите алгоритм составления таблицы умножения в Р-ичной системе счисления.
Заключение
Сегодня многими учеными высказывается
утверждение, что элементная база компьютерной техники, основанная на двоичном
кодировании, скоро достигнет границы своих возможностей, и тогда, скорее всего,
дальнейшее развитие этой области науки и техники будет связано с новыми
математическими результатами в области кодирования информации. В ХХ веке в
теории чисел системам счисления не уделялось должного внимания, и в этой части
данная теория не намного ушла вперед по сравне![]() нию с периодом своего
зарождения. Это было связано с отсутствием серьезной потребности в
использовании новых систем счисления в практике вычислений, которая в течение
последних столетий всецело удовлетворялась десятичной системой, а в последние
десятилетия — двоичной системой (в информатике).
нию с периодом своего
зарождения. Это было связано с отсутствием серьезной потребности в
использовании новых систем счисления в практике вычислений, которая в течение
последних столетий всецело удовлетворялась десятичной системой, а в последние
десятилетия — двоичной системой (в информатике).
Ситуация резко изменилась в результате появления современных компьютеров. Именно в информатике опять проявился интерес к способам представления чисел и к новым компьютерным арифметикам. Дело в том, что, как мы уже говорили, классическая двоичная система счисления обладает рядом принципиальных недостатков, главными из которых являются проблема представления отрицательных чисел и нулевая избыточность.
В связи с этим изучение основ построения систем счисления, свойств различных систем счисления представляет сегодня не только научный, но и практический интерес.
В заключение хотелось бы отметить, что научные исследования в области систем счисления продолжаются. Математики, например, изучают нега-позиционные системы счисления, основаниями которых являются целые отрицательные числа, а также системы с основанием, содержащим мнимую единицу и т. д. Не исключено, что кому-то из вас удастся сказать свое слово в этих областях математики и информатики.
Глава 2
![]()
Представление информации в компьютере
![]()
В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль — небытие, и что высшее су-
![]()
ЩеСТВО создает все супцее из небытия точно таким же образом, как единица и нуль в его системе выражают все числа.
П. С. Лаплас
Очень легко делать удивительные открытин, но трудно усовершенствовать их в такой степени, чтобы они получили практическую ценность.
Т. А. эдисон
S 2.1. Представление целых чисел
S 2.2. Представление вещественных чисел
S 2.3. Представление текстовой информации
S 2.4. Представление графической и видеоинформации
S 2.5. Представление звуковой информации
S 2.6. Методы сжатия цифровой информации
конца ХХ века, века компьютеризации,
человече![]() ство ежедневно пользуется двоичной
системой счисления, так как вся информация, обрабатываемая современными
компьютерами, представлена в двоь
ство ежедневно пользуется двоичной
системой счисления, так как вся информация, обрабатываемая современными
компьютерами, представлена в двоь ![]() ичном виде.
ичном виде.
Каждый регистр арифметического устройства компьютера, каждая ячейка памяти представляет собой физическую систему, состоящую из некоторого числа однородных элементов, обладающих двумя устойчивыми состояниями, одно из которых соответствует нулю, а другое — единице. Каждый такой элемент служит для записи одного из разрядов двоичного числа. Именно поэтому каждый элемент ячейки называют разрядом.
(К — 1)-й разряд О-й разряд

ячейка из К разрядов
В данной главе мы рассмотрим, каким образом решается проблема преобразования исходной информации в компьютерное представление для каждого вида информации. Будет показано, насколько точно компьютерное представление отражает исходную информацию, причем слово «точно» здесь применяется не только к числам (точность представления), но и к другим видам информации. А именно, рассматривается степень реалистичности передачи оттенков цвета на мониторе, степень приближенности воспроизводимой музыки к естественному звучанию музыкальных инструментов или голосу человека и т. д. Задача перевода информации естественного происхождения в компьютерную называется задачей Дискретизации или квантования. Эту задачу необходимо решать для всех видов информации. Способы дискретизации для разных видов информации различны, но подходы к решению этой задачи построены на одинаковых принципах.
S 2.1 . Представление целых чисел
Введение специальных способов представления целых чисел оправдано тем, что достаточно часто в задачах, решаемых с помощью компьютера, многие действия сводятся к операциям над целыми числами. Например, в задачах экономического характера данными служат количества акций, сотрудников, деталей, транспортных средств и т. д., по своему смыслу являющиеся целыми числами. Целые числа используются и для обозначения даты и времени, и для нумерации различных объектов: элементов массивов, записей в базах данных, машинных адресов и т. п.
![]() Для компьютерного
представления целых чисел обычно используется несколько различных способов
представления, отличающихся друг от друга количеством разрядов и наличием или
отсутствием знакового разряда. Беззнаковое представление можно использовать
только для неотрицательных целых чисел, отрицательные числа представляются
только в знаковом виде.
Для компьютерного
представления целых чисел обычно используется несколько различных способов
представления, отличающихся друг от друга количеством разрядов и наличием или
отсутствием знакового разряда. Беззнаковое представление можно использовать
только для неотрицательных целых чисел, отрицательные числа представляются
только в знаковом виде.
При беззнаковом представлении все разряды ячейки отводятся под само число. При представлении со знаком самый старший (левый) разряд отводится под знак числа, остальные разряды под собственно число. Если число положительное, то в знаковый разряд помещается О, если число отрицательное — 1. Очевидно, в ячейках одного и того же размера можно представить больший диапазон целых неотрицательных чисел в беззнаковом представлении, чем чисел со знаком. Например, в одном байте (8 разрядов) можно записать положительные числа от О до 255, а со знаком — только до 127. Поэтому, если известно заранее, что некоторая числовая величина всегда является неотрицательной, то выгоднее рассматривать ее как беззнаковую.
![]() Говорят,
что целые числа в компьютере хранятся в
Говорят,
что целые числа в компьютере хранятся в
формате с фиксированной запятой.
2.1 в 1 . Представление целых положительных чисел
Максимально представимому числу
соответствуют единицы во всех разрядах ячейки (двоичное число, со![]() стоящее из К
единиц). Для К-разрядного представления оно будет равно 2 — 1. Минимальное
число представляется нулями во всех разрядах ячейки, оно всегда равно нулю.
Ниже приведены максимальные числа для беззнакового представления при различных
значениях К:
стоящее из К
единиц). Для К-разрядного представления оно будет равно 2 — 1. Минимальное
число представляется нулями во всех разрядах ячейки, оно всегда равно нулю.
Ниже приведены максимальные числа для беззнакового представления при различных
значениях К:
|
Количество разрядов |
Максимальное число |
|
|
8 |
255 (2 8 - 1) |
|
|
16 |
65535 (2 16 |
1) |
|
32 |
4294967295 (2 32 |
1) |
|
|
18446744073709551615 (2 64 |
1) |
При знаковом представлении целых чисел возникают такие понятия, как прямой, обратный и дополнительный коды.
определение 1. Представление числа в привычной для
человека форме «знак—величина», при которой старший раз- ![]()
![]() ряд ячейки отводится
под знак, остальные К — 1 разрядов — под цифры числа, называется прямым кодом.
ряд ячейки отводится
под знак, остальные К — 1 разрядов — под цифры числа, называется прямым кодом.
Например, прямые коды двоичных чисел 110012 и —110012 для восьмиразрядной ячейки равны 00011001 и
![]()
10011001 соответственно. Положительные
целые числа представляются в компьютере с помощью прямого кода. Прямой код
отрицательного целого числа отличается от прямого кода соответствующего
положительного числа содержимым знакового разряда. Но вместо прямого кода ![]() для
представления отрицательных целых чисел в компьютере используется
дополнительный код (см. п. 2.1.2).
для
представления отрицательных целых чисел в компьютере используется
дополнительный код (см. п. 2.1.2).
Отметим, что максимальное положительное
число, ![]() которое можно записать в знаковом
представлении в К
которое можно записать в знаковом
представлении в К
К-1
разрядах, равно 2 1, что практически в два раза ![]() меньше
максимального числа в беззнаковом представлении в тех же К разрядах.
меньше
максимального числа в беззнаковом представлении в тех же К разрядах.
![]()
Решение. Максимальное положительное
число в 8 битах равно 127 (2 7 — 1), в 16 битах — 32767 (2 15![]()
Пример 1. Число 53 = 1101012 в восьмиразрядном представлении имеет вид:
|
0 0 1 1 0 1 0 1 |
Это же число 53 в 16 разрядах будет записано следующим образом:
0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1
В обоих случаях неважно, знаковое или беззнаковое представление при этом используется.
Пример 2. Для числа 200 = 110010002 представление в 8 разрядах со знаком невозможно, так как максимальное допустимое число в таком представлении равно 127, а в беззнаковом восьмиразрядном представлении оно имеет вид:
2.1 .2. Представление целых отрицательных чисел
Для представления в компьютере целых отрицательных чисел используют дополнительный код, который позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно увеличивает скорость вычислений. Прежде чем вводить определение дополнительного кода, сделаем следующее важное замечание.
![]() В К—разрядной целочисленной компьютерной арифметине 2
В К—разрядной целочисленной компьютерной арифметине 2![]()
Объяснить это можно тем, что двоичная
запись числа 2 k состоит из одной единицы и К нулей, а в ячейку из К
![]() разрядов
может уместиться только К цифр, в данном случае только К нулей. В таком случае
говорят, что значащая единица вышла за пределы разрядной сетки.
разрядов
может уместиться только К цифр, в данном случае только К нулей. В таком случае
говорят, что значащая единица вышла за пределы разрядной сетки.
Разберемся, что и до чего дополнительный
код дополняет. Дополнительный код отрицательного числа т ![]() это
дополнение модуля этого числа до 2 h (или до нуля в К-разрядной
арифметике): (2 k — lml) + lml = 2 k О.
это
дополнение модуля этого числа до 2 h (или до нуля в К-разрядной
арифметике): (2 k — lml) + lml = 2 k О.
Алгоритм получения дополнительного К-разрядного кода отрицательного числа
1. Модуль числа представить прямым кодом в К двоичных разрядах.
2. Значения всех разрядов инвертировать (все нули заменить на единицы, а единицы — на нули), получив, таким образом, К—разрядный обратный код исходного числа.
З. К полученному обратному коду, трактуемому как К—разрядное неотрицательное двоичное число, прибавить единицу.
Обратный код является дополнением исходного числа до числа 2 — 1, состоящего из К двоичных единиц. Поэтому прибавление единицы к инвертированному коду позволяет получить его искомый дополнительный код.
Пример З. Получим дополнительный код числа —52 для восьми- и шестнадцатиразрядной ячеек.
Для восьмиразрядной ячейки:
0011 0100 — прямой код числа 1—52! = 52;
1100 1011 обратный код числа —52;
1100 1100 — дополнительный код числа —52. Для шестнадцатиразрядной ячейки:
0000 0000 0011 0100 — прямой код числа 1—521;
![]() — обратный код числа —52;
— обратный код числа —52;
Вопрос. Какое минимальное отрицательное число можно записать в К разрядах?
Ответ. Описанный выше алгоритм получения дополнительного
кода для отрицательного числа знаковую единињу_ в ![]() левом разряде
образует автоматически при lml 2
левом разряде
образует автоматически при lml 2
Представим значение 2 k — lml в следующем виде:
![]() Д).
Д).
Здесь первое слагаемое 2 соответствует
единице в левом знаковом разряде. То есть при представлении отрицательного
числа т дополнительным кодом в самом левом (знаковом) разряде записывается знак
отрицательного числа (единица), а в остальных разрядах ![]()
К—1
число 2 lml. Следовательно, минимальное отрицательное (максимальное по модулю) число т, которое
К-1
можно представить в К разрядах, равно —2 (это ограничение и было приведено в определении 2).
Задание. Постройте Дополнительный восьмиразряДный код для чисел —128, —127 и —0.
Решение. Ответы приведены в таблице ниже:
|
Число |
-128 |
-127 |
—0 |
|
Прямой код модуля Обратный код |
1000 0000 |
1000 0000 |
0000 0000 |
|
Дополнительный код |
1000 0000 |
1000 0001 |
0000 0000 |
Отметим, что для числа —128 прямой код совпадает с дополнительным, а дополнительный код числа —0 совпадает с обычным нулем. При преобразовании обратного кода для числа —0 в его дополнительный код правила обычной двоичной арифметики нарушаются, а именно:
![]()
Восстановить модуль исходного десятичного отрицательного числа по его дополнительному коду можно двумя способами.
Способ 1 (обратная цепочка
преобразований): вычесть единицу из дополнительного кода, инвертировать
полученный код и перевести полученное двоичное представ![]() ление числа в
десятичное.
ление числа в
десятичное.
Способ 2: по приведенному выше алгоритму построить дополнительный код для имеющегося дополнительного кода искомого числа и представить результат в десятичной системе счисления.
Способ 1 :
1) из дополнительного кода вычтем 1:
10010111 — 1 = 10010110 (получили обратный код);
2) инвертируем полученный код: 01101001 (получили модуль отрицательного числа);
З) переведем полученное двоичное значение в десятичную систему счисления:
011010012 = 2 6 + 2 5 + 2 3 + 1 = 64 + 32 + 8 + 1 = 105. Ответ: —105.
Способ 2:
1) инвертируем имеющийся дополнительный код:
01101000;
2) прибавим к результату 1: 01101000 + 1 01101001 (получили модуль отрицательного числа);
З) переведем полученное двоичное значение в десятичную систему счисления:
011010012 = 2 6 + 2 5 + 2 3 + 1 = 64 + 32 +8+ 1 - 105. Ответ: —105.
Целые числа со знаком, пуедставимые в К разрядах, принадлежат диапазону [—2 — 1], который не является симметричным относительно 0, Это следует учитывать при программировании. Если, например, изменить знак у наибольшего по модулю отрицательного числа, то полученный результат окажется уже не представимым в том же числе разрядов.
Ниже приведены значения границ диапазонов для знаковых представлений в ячейках с различной разрядностью:
|
Разрядность |
Минимальное число |
Максимальное число |
|
8 |
-128 |
127 |
|
16 |
-32768 |
32767 |
|
32 |
-2147483648 |
2147483647 |
|
|
-9223372036854775808 |
9223372036854775807 |
2.1 .З. Перечисление чисел в целочисленной компьютерной арифметике
![]()
О 1 2 255
Для восьмиразрядного знакового представления:
![]()
-128 -127 -1 О 1 2 127
![]() Однако в К—разрядной компьютерной
арифметике эти
Однако в К—разрядной компьютерной
арифметике эти ![]() отрезки можно замкнуть в кольца и
перечислять числа соответствующего представления по кругу.
отрезки можно замкнуть в кольца и
перечислять числа соответствующего представления по кругу.
![]() Все целые числа
любого К—разрядного представления можно зафиксировать на кольце по порядку,
причем рядом с максимальным числом в том или ином представлении будет
находиться минимальное, например:
Все целые числа
любого К—разрядного представления можно зафиксировать на кольце по порядку,
причем рядом с максимальным числом в том или ином представлении будет
находиться минимальное, например:
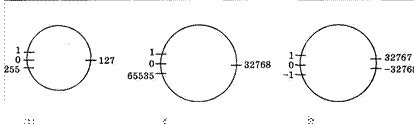
беззнаковое беззнаковое знаковое
Действительно, результатом прибавления единицы в арифметике с фиксированным количеством разрядов является следующее по часовой стрелке за исходным значение на кольце, а результатом вычитания единицы — следующее значение по ходу против часовой стрелки. Данный факт очевиден, кроме случаев перехода от максимально допустимого числа к минимальному при прибавлении единицы и от минимального к максимальному при вычитании.
![]()
![]() Поясним эти
случаи. Рассмотрим вначале беззнаковые представления. Максимально допустимое
число в К—разрядном беззнаковом представлении равно 2 1 и состоит из К единиц в
двоичном представлении. При прибавлении к такому числу единицы мы получаем 2 ,
что в свою очередь соответствует нулю в К-разрядной арифметике. Вычитание же из
нуля единицы является обратной опера
Поясним эти
случаи. Рассмотрим вначале беззнаковые представления. Максимально допустимое
число в К—разрядном беззнаковом представлении равно 2 1 и состоит из К единиц в
двоичном представлении. При прибавлении к такому числу единицы мы получаем 2 ,
что в свою очередь соответствует нулю в К-разрядной арифметике. Вычитание же из
нуля единицы является обратной опера![]() цией: вычитание единицы можно
рассматривать и как
цией: вычитание единицы можно
рассматривать и как ![]() прибавление к нулю минус единицы, по
правилам же К—разрядной арифметики «минус единица» — это дополнение единицы 40
2 k , т. е. число, которое при сложении с единицей даст 2 .
Очевидно, что таковым является число
прибавление к нулю минус единицы, по
правилам же К—разрядной арифметики «минус единица» — это дополнение единицы 40
2 k , т. е. число, которое при сложении с единицей даст 2 .
Очевидно, что таковым является число ![]() — 1, состоящее из К двоичных единиц,
значит, в беззнаковом представлении О + (—1) 2 k 1, что является
максимально представимым числом .
— 1, состоящее из К двоичных единиц,
значит, в беззнаковом представлении О + (—1) 2 k 1, что является
максимально представимым числом .
В знаковом К—разрядном представлении
максимально допустимым является число 2к - [1]
— 1 (К — 1 двоичная единица). При увеличении такого числа на 1 мы
получаем ![]() , или единицу в знаковом бите и нули в
остальных, что соответствует отрицательному числу с максимально возможным
модулем. Вычитание единицы из такого
, или единицу в знаковом бите и нули в
остальных, что соответствует отрицательному числу с максимально возможным
модулем. Вычитание единицы из такого
числа можно проводить по правилам обычной двоичной арифметики: 1 0...0 — 1 = О 1...1 = 2К - 1.
К-1
Достоинством рассмотренных форматов представления целых чисел является простота реализации алгоритмов арифметических операций (например, вычитание, благодаря использованию дополнительного кода для представления отрицательных чисел, сводится к сложению).
2.1 .4. Особенности реализации арифметических операций в конечном числе разрядов
Целочисленная арифметика в ограниченном числе разрядов несколько отличается от обычной. При выполнении арифметических действий в целочисленной К-разрядной арифметике возможно возникновение следующих ситуаций, незнание которых может привести к неверному результату при выполнении верных алгоритмов:
Пример 5. Выполним сложение 100 10 и
5110 в знаковом восьмиразрядном представлении. В этом представлении числа имеют
следующий вид: 10010 0110 01002 и 5110![]()
![]() 0011 00112. При сложении этих чисел получим 1001 01112. Самая левая
единица (знаковый разряд) указывает на то, что в 8 разрядах записано
отрицательное штсло.
0011 00112. При сложении этих чисел получим 1001 01112. Самая левая
единица (знаковый разряд) указывает на то, что в 8 разрядах записано
отрицательное штсло.
Так как все отрицательные числа в машине представляются дополнительным кодом, то для восстановления десятичного значения этого отрицательного числа надо воспользоваться алгоритмом получения исходного числа по его дополнительному коду (см. пример 4). В результате получим число —105.
Таким рбразом, в восьмиразрядной знаковой арифметике 100 + 51 — —105, т. е. при сложении двух положительных чисел мы получили отрицательное число! 2
Вопросы и задания
1. Обоснуйте целесообразность представления особым образом в компьютере целых чисел.
2. Приведите пример умножения в ограниченном числе разрядов двух положительных чисел, в результате которого получается отрицательное число.
З. Перечислите и объясните все ошибки, которые могут возникать при выполнении арифметических операций над целыми числами в компьютерной арифметике в ограниченном числе разрядов.
4. Покажите,
каким образом использование дополнительного кода позволяет заменить операцию
вычитания опе![]() рацией сложения.
рацией сложения.
5. В восьмиразрядной ячейке запишите дополнительные коды следующих двоичных чисел:
а) -1010; 6) -1001; в) -11; г) -11011.
6. Можно ли по виду дополнительного кода числа сказать, четно оно или нечетно?
7.
![]()
8. Какие из чисел 4316, 1010102 , 12910 и —13510 можно сохранить в одном байте (в 8 разрядах)?
9. Получите 16-разрядное представление следующих чисел:
а) 25; 6) -610.
10. Для чисел А = 11102, В = 11012 выполните следующие операции: А + В; А — В; В — А; —А — А; —В — В; —А — В (в восьмиразрядном знаковом представлении).
11. Вычислите с помощью Инженерного калькулятора (стандартное приложение Windows) следующие выражения:
а) 1110111012 11011101102,
6) 11011010012 110001001002.
Как вы можете объяснить полученные результаты?
S 2.2. Представление вещественных чисел
Вещественные числа в компьютере хранятся в формате с плавающей запятой, который опирается на нормализованную форму записи чисел.
![]()
2.2.1 . Нормализованная запись числа
Если при представлении целых чисел в компьютере ограничением может служить лишь величина записываемого числа, то при записи вещественного числа речь в первую очередь идет о точности его представления, т. е. о количестве значащих цифр, которые удается сохранить в ограниченном числе разрядов.
![]() Пример 6. Допустим, мы имеем калькулятор, в котором на
экране дисплея для вывода чисел есть только 10 знако
Пример 6. Допустим, мы имеем калькулятор, в котором на
экране дисплея для вывода чисел есть только 10 знако![]() мест (включая знак
числа и запя
мест (включая знак
числа и запя![]() тую между целой и дробной частя
тую между целой и дробной частя![]() ми
десятичного числа). Если нам необходимо работать с числами
ми
десятичного числа). Если нам необходимо работать с числами
-6392000000; -639,2;
-0,0000006392,
то на дисплее нашего калькулятора отобразить удастся лишь второе из них (первое число занимает 11 знакомест, второе 6 знакомест, третье — 13 знакомест).
Эта задача может быть решена, если числа
предста![]() вить несколько иначе. Забегая вперед,
скажем, что для примера 6 искомый способ записи чисел в калькуляторе таков .
вить несколько иначе. Забегая вперед,
скажем, что для примера 6 искомый способ записи чисел в калькуляторе таков .
-6.З92Е+9 -6.З92Е+О2 -6.З92Е-О7,
![]() где знак «Е» читается
как «умножить на десять в степени». Такая запись отражает экспоненциальную
форму записи чисел.
где знак «Е» читается
как «умножить на десять в степени». Такая запись отражает экспоненциальную
форму записи чисел.
Определение З. Любое число а в
экспоненциальной форме представляется в виде а = +mxPq, где Р —
основание системы счисления, т называется мантиссой числа, q ![]() поряДком
числа.
поряДком
числа.
![]()
В калькуляторе, как и во многих компьютерных программах, вместо запятой для отделения дробной части от целой используется точка. Это соответствует западной традиции записи Р-ичных чисел.
Пример 7. Длину отрезка, равного 47,8 см, в экспоненциальной форме записи можно представить так:
1) 478 х 10 -1 см = 478 мм;
2) 4,78 х 10 1 см = 4,78 дм;
3) 47,8 х 10 0 см = 47,8 см;
4) 0,478 х 10 2 см = 0,478 м. 2
Из этого примера видно, что длину одного и того же отрезка можно записать с использованием различных экспоненциальных форм. Эта неоднозначность записи может приводить в определенных случаях к неудобству. Из курса алгебры известно, что если Р фиксировано и 1 /Р S т < 1, то представление числа в экспоненциальной форме единственно. Такая форма экспоненциального представления называется нормализованной формой и используется в компьютере для однозначности представления вещественных чисел.
![]()
![]()
Заметим, что число ноль не может быть записано в нормализованной форме так, как она была определена. Поэтому относительно нормализованной записи нуля приходится прибегать к особым соглашениям. Условимся, что запись нуля является нормализованной, если и мантисса, и порядок равны нулю.
В нормализованной форме все числа записываются одинаково в том смысле, что запятая у них ставится в одном и том же месте — перед первой (самой левой) значащей цифрой мантиссы. Заметим, что в двоичной системе счисления первая цифра мантиссы нормализованного числа всегда равна 1 (за исключением числа ноль). Величина же числа (т. е. ее порядок) указывается отдельно, с помощью соответствующей степени основания системы счисления, в которой это число было записано изначально. Количество цифр в мантиссе может оказаться меньше, чем число значащих цифр в исходном числе. Часто в нормализованной записи мантисса Р-ичного числа записывается в Р—ичной системе счисления, а порядок и само число Р — в десятичной.
Пример 8. Приведем примеры нормализации чисел:
1) О = 0,0 х 100 (возможная нормализация нуля);
2) 3,1415926 = 0,31415926 х 10 1 (количество значащих цифр не изменилось);
З) 1000 = 0,1 х 104 (количество значащих цифр уменьшилось с четырех до одной);
4) 0,123456789 = 0,123456789 х 10 0 (запятую передвигать не нужно);
5) 0,00001078 — - О ,1078 х 8- (количество значащих цифр уменьшилось с семи до трех);
6) 1000,00012 = О ,100000012 х 2 4 (количество значащих цифр уменьшить невозможно);
7) AB,CDEF16 = 0,ABCDEF16 х 16 2 (количество значащих цифр уменьшить невозможно).
При записи нормализованного числа в компьютере или калькуляторе для записи мантиссы и порядка отводится заранее фиксированное количество разрядов.
Поясним это на примере школьного
калькулятора, который производит вычисления в десятичной системе счисления.
Пусть это будет калькулятор с десятью знакоместами на дисплее, мантисса в нем
имеет четыре цифры, порядок — две. В отличие от стандартной нормализации, у
калькуляторов первая значащая цифра, с которой и начинается мантисса,
изображает![]() ся перед точкой. Порядок при этом
соответственно уменьшается на единицу. Такая форма записи нормализованных чисел
позволяет экономить одно знакоместо, так как вместо нуля в целой части мы
помещаем значащую цифру.
ся перед точкой. Порядок при этом
соответственно уменьшается на единицу. Такая форма записи нормализованных чисел
позволяет экономить одно знакоместо, так как вместо нуля в целой части мы
помещаем значащую цифру.
Пример 9
1) Число 248,53786 в калькуляторе превращается в +2.485Е+О2. Переводя последнее число в привычное представление с фиксированной запятой, получим +248,5.
2) Число —2485378600,0 в калькуляторе превращается в —2.485Е+О9. Переводя последнее число в привычное представление с фиксированной запятой, получим -2485000000.
З) Число 0,00024853786 в калькуляторе имеет вид +2.485Е—О4, т. е. равно числу 0,0002485.
Следовательно, всякое десятичное число, состоящее не более чем из четырех значащих цифр в нормализованном виде, можно представить в таком калькуляторе точно, а остальные числа — лишь приближенно.
В первом пункте примера 9 погрешность калькуляторного представления исходного числа составила 248,53786 — 248,5 = 0,03786. Во втором пункте погрешность равна 2485378600 2485000000 378600, а в третьем — 0,00024853786 - 0,0002485 = 0,00000003786. Если бы мантисса калькулятора имела больше цифр, погрешность была бы меньше.
Несмотря на то, что в абсолютном исчислении погрешность может быть значительно больше 1, относительно величины самого числа ее порядок остается неизменным. Относительная погрешность представления чисел в примере 9 равна:
![]() 0,00015233...
0,00015233...
378600/2485378600 = 0,00015233...
![]() =
0,00015233...
=
0,00015233... ![]()
Определение 6. Относительной
погрешностью представления х называют величину ![]()
Вопрос. Как вы Думаете, что нам Дает знание величин абсолютной и относительной погрешности при решении реальных задач на компьютере?
Ответ. Абсолютная погрешность говорит о том, на сколько полученный результат (например, результат представления числа в компьютере) отличается от истинного результата (в нашем примере от самого числа).
При решении реальных задач знание этой величины позволяет оценивать, насколько достоверный результат был получен. Если его точность нас не удовлетворяет, то следует выбрать другой (более точный) способ представления чисел.
Относительная же погрешность показывает,
сколько ![]() верных старших значащих цифр содержит
результат. В примере 9 относительная погрешность представления разных по
величине чисел равна 0,00015233... Такая относительная погрешность означает,
что мы имеем три безусловно верные значащие цифры результата. Значение
относительной погрешности непосредственно связано с количеством разрядов,
отводимых для представления мантиссы нормализованного числа.
верных старших значащих цифр содержит
результат. В примере 9 относительная погрешность представления разных по
величине чисел равна 0,00015233... Такая относительная погрешность означает,
что мы имеем три безусловно верные значащие цифры результата. Значение
относительной погрешности непосредственно связано с количеством разрядов,
отводимых для представления мантиссы нормализованного числа.
На практике обычно известна относительная погрешность представления чисел, так как разрядность мантиссы фиксирована. Следовательно, можно предположить, сколько верных цифр содержит результат. Если из каких-то априорных соображений известно значение вычисляемой величины, то можно оценить абсолютную погрешность результата. 2
![]() В компьютерной записи вещественных чисел с плавающей
запятой количество цифр, отводимых под запись порядка, определяет, насколько
большие и насколько маленькие положительные числа могут быть представлены .
В компьютерной записи вещественных чисел с плавающей
запятой количество цифр, отводимых под запись порядка, определяет, насколько
большие и насколько маленькие положительные числа могут быть представлены .
Покажем это опять на примере школьного калькулятора. В формате нашего калькулятора порядок имеет две цифры, и наибольшее число, которое может быть в нем представлено, — это +9.999Е+99. Если бы нам пришлось записать это число в формате с фиксированной запятой, оно имело бы ровно 100 цифр до запятой (четыре девятки и 96 нулей), т. е. это и в самом деле очень большое число.
А самое маленькое положительное число, которое можно ввести в нашем калькуляторе, — это +1.OOOE-99. В формате с фиксированной запятой оно имеет 99 десятичных знаков после запятой, а именно 98 нулей и единицу. Это очень маленькое число. Таким образом, выраэкая порядок лишь двумя десятичными цифрами, можно записывать числа из очень широкого диапазона.
2) Число —2485378600,0 в калькуляторе превращается в —2.485Е+О9, Переводя последнее число в привычное представление с фиксированной запятой, получим -2485000000.
З) Число 0,00024853786 в калькуляторе имеет вид +2.485Е—О4, т. е. равно числу 0,0002485.
Следовательно, всякое десятичное число, состоящее не более чем из четырех значащих цифр в нормализованном виде, можно представить в таком калькуляторе точно, а остальные числа — лишь приближенно.
В первом пункте примера 9 погрешность калькуляторного представления исходного числа составила 248,53786 — 248,5 = 0,03786. Во втором пункте погрешность равна 2485378600 2485000000 378600, а в третьем — 0,00024853786 - 0,0002485 = 0,00000003786. Если бы мантисса калькулятора имела больше цифр, погрешность была бы меньше.
![]()
Несмотря на то, что в абсолютном исчислении погрешность может быть значительно больше 1, относительно величины самого числа ее порядок остается неизменным. Относительная погрешность представления чисел в примере 9 равна:
![]() = 0,00015233...
= 0,00015233...
378600/2485378600 = 0,00015233...
![]() = 0,00015233...
= 0,00015233...
|
|
|
х |
Определение 6. Относительной погрешностью представления х называют величину
Вопрос. Как вы Думаете, что нам Дает знание величин абсолютной и относительной погрешности при решении реальных задач на компьютере?
Ответ. Абсолютная погрешность говорит о том, на сколько полученный результат (например, результат представления числа в компьютере) отличается от истинного результата (в нашем примере от самого числа).
При решении реальных задач знание этой величины позволяет оценивать, насколько достоверный результат был получен. Если его точность нас не удовлетворяет, то следует выбрать другой (более точный) способ представления чисел.
Относительная же погрешность
показывает, сколько верных старших значащих цифр содержит результат. ![]() В
примере 9 относительная погрешность представления разных по величине чисел
равна 0,00015233... Такая относительная погрешность означает, что мы имеем три
безусловно верные значащие цифры результата. Значение относительной погрешности
непосредственно связано с количеством разрядов, отводимых для представления
мантиссы нормализованного числа.
В
примере 9 относительная погрешность представления разных по величине чисел
равна 0,00015233... Такая относительная погрешность означает, что мы имеем три
безусловно верные значащие цифры результата. Значение относительной погрешности
непосредственно связано с количеством разрядов, отводимых для представления
мантиссы нормализованного числа.
![]()
![]() В компьютерной записи вещественных чисел с плавакощей
запятой количество цифр, отводимых под запись порядка, определяет, насколько
большие и насколько маленькие положительные числа могут быть представлены.
В компьютерной записи вещественных чисел с плавакощей
запятой количество цифр, отводимых под запись порядка, определяет, насколько
большие и насколько маленькие положительные числа могут быть представлены.
Покажем это опять на примере школьного калькулятора. В формате нашего калькулятора порядок имеет две цифры, и наибольшее число, которое может быть в нем представлено, — это +9.999Е+99. Если бы нам пришлось записать это число в формате с фиксированной запятой, оно имело бы ровно 100 цифр до запятой (четыре девятки и 96 нулей), т. е. это и в самом деле очень большое число.
А самое маленькое положительное число,
которое можно ввести в нашем калькуляторе, — это +1.OOOE-99. В формате с
фиксированной запятой оно имеет 99 десятичных знаков после запятой, а именно 98
нулей и единицу. Это очень маленькое число. Таким образом, выра![]() экая порядок
лишь двумя десятичными цифрами, можно записывать числа из очень широкого
диапазона.
экая порядок
лишь двумя десятичными цифрами, можно записывать числа из очень широкого
диапазона.
Широкий диапазон представления чисел с плавающей запятой необходим при решении научных и инженерных задач. Такое представление чисел не только позволяет сохранять в разрядной сетке большое количество значащих цифр и тем самым повышать точность вычислений, но также упрощает действия над порядками и мантиссами.
2.2.2. Представление вещественных чисел в формате с плавающей запятой
Как и для целых чисел, при представлении
вещественных чисел в компьютере используется чаще всего двоич![]() ная система
счисления, следовательно, предварительно десятичное число должно быть
переведено в двоичную систему, а уж затем представлено в нормализованной форме
с Р = 2.
ная система
счисления, следовательно, предварительно десятичное число должно быть
переведено в двоичную систему, а уж затем представлено в нормализованной форме
с Р = 2.
Например, можно представить себе такое распределение разрядов ячейки памяти:
![]()
Первые два разряда служат для представления знаков порядка (s ) и мантиссы (sm) соответственно. Следующие К разрядов используются для представления абсолютной величины порядка числа ф), остальные п разрядов — для представления абсолютной величины мантиссы. В каждом разряде ячейки может храниться одно из двух значений: О или 1.
Тогда изображенному на схеме состоянию ячейки соответствует число
![]() где q
где q 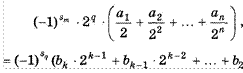 1
1 ![]()
При такой системе записи наибольшее по
абсолютной величине число, которое может быть представлено в машине, равно 2 •
(1 — 2 -п ), а наименьшее по абсолютной ![]() величине число,
отличное от нуля, равно 2 - 2 -2
величине число,
отличное от нуля, равно 2 - 2 -2![]()
Вещественных чисел, точно представимых в компьютере, конечное число. Остальные числа либо приближаются представимыми, либо оказываются непредставимыми. Последнее относится к слишком большим и к слишком маленьким вещественным числам.
2.2.31 Выполнение арифметических операций над вещественными числами
Использование в компьютере представления чисел в формате с плавающей запятой усложняет выполнение арифметических операций.
![]()
Пусть а = х 2 % , Ь = х 2 0 — два норма-
лизованных двоичных числа, и qa Ъ. Результатом их сложения
или вычитания будет являться следующее выражение: С = (О, Т О, ТЬ Х![]()
После операций над порядками и мантиссами мы получаем порядок и мантиссу результата, но последняя, вообще говоря, может не удовлетворять ограничениям, накладываемым на мантиссы нормализованных чисел. Так как от результата арифметических операций в компьютере требуется, чтобы он также был нормализованным числом, необходимо дополнительное преобразование результата — нормализация. В зависимости от величины получившейся мантиссы результата, она сдвигается вправо или влево так, чтобы ее первая значащая цифра попала в первый разряд после запятой. Одновременно порядок результата увеличивается или уменьшается на число, равное величине сдвига.
![]() Заметим, что над
мантиссами в арифметическом устройстве могут выполняться все четыре
арифметических действия, а также операции сдвига, тогда как над порядками
производятся только действия сложения и вычитания. Отрицательные порядки можно
записывать в дополнительном коде для того, чтобы операцию вычитания свести к
операции сложения.
Заметим, что над
мантиссами в арифметическом устройстве могут выполняться все четыре
арифметических действия, а также операции сдвига, тогда как над порядками
производятся только действия сложения и вычитания. Отрицательные порядки можно
записывать в дополнительном коде для того, чтобы операцию вычитания свести к
операции сложения.
![]() В ряде случаев, даже
если некоторые два числа были представлены в формате с плавающей запятой
абсолютно точно, результат выполнения над ними арифметических операций часто
может содержать погрешность, а иногда может быть заведомо неверным.
В ряде случаев, даже
если некоторые два числа были представлены в формате с плавающей запятой
абсолютно точно, результат выполнения над ними арифметических операций часто
может содержать погрешность, а иногда может быть заведомо неверным.
Поясним более подробно особенности выполнения арифметических операций над вещественными числами на примерах. При этом будем считать, что в записи вещественного числа с плавающей запятой один разряд отводится под десятичный порядок и пять разрядов — под десятичную мантиссу.
Так как порядки у чисел различны, то перед сложением производится выравнивание порядков. Число с меньшим порядком преобразуется в число с порядком, равным порядку другого слагаемого (меньший порядок «приводится» к большему). В данном случае второе слагаемое будет преобразовано к виду 0,00071824 х 10 2 , после чего выполняется сложение.
10 2 х 0,23619
+ 10 2 х 0,00071824
10 2 х 0,23690824
Результат получили с ббльшим числом разрядов, чем вмещает ячейка, поэтому он округляется и записывает-
2
ся в памяти в виде 0,23691 х 10 .
Пример 11. Выполним сложение двух вещественных чисел: 0,23619 х 10 8 и 0,91824 х 10 8 .
Так как порядки у этих чисел одинаковы, то производить операцию выравнивания порядков не требуется. Операция сложения сводится к сложению мантисс.
108 х 0,23619
+ 108 х 0,91824
108 х 1,15443
![]()
Результат ненормализованное число 1,15443 х 10 8 . Требуется выполнить нормализацию путем сдвига мантиссы вправо на один разряд, а затем округление результата, так как в мантиссе будет уже шесть цифр, а в ячейке памяти под мантиссу отведено их только пять. Ответ: 0,11544 х 109 .
Пример 12. Выполним сложение двух
вещественных чисел, одно из которых достаточно большое по сравнению со вторым:
0,23619 х 103 и 0,91824 х 10-3![]()
Так как порядки у этих чисел различны,
то требуется ![]() произвести предварительную операцию их
выравнивания. После выполнения выравнивания порядков складываться будут
следующие числа:
произвести предварительную операцию их
выравнивания. После выполнения выравнивания порядков складываться будут
следующие числа:
103 х 0,23619
+ 103 х 0,00000091824
10 3 х 0,23619091824
![]() В вещественной компьютерной арифметике с ограниченным
числом разрядов 1 + г = 1 при 0 < Е < 2 , где п — количество разрядов,
отводимых для представления мантиссы вещественного числа.
В вещественной компьютерной арифметике с ограниченным
числом разрядов 1 + г = 1 при 0 < Е < 2 , где п — количество разрядов,
отводимых для представления мантиссы вещественного числа.
![]() При умножении двух целых чисел с плавающей
запя
При умножении двух целых чисел с плавающей
запя![]() той их порядки необходимо просто сложить,
а мантиссы перемножить (предварительное выравнивание не производится). При
Делении из порядка делимого надо
той их порядки необходимо просто сложить,
а мантиссы перемножить (предварительное выравнивание не производится). При
Делении из порядка делимого надо ![]() вычесть порядок делителя, а мантиссу
делимого разделить на мантиссу делителя.
вычесть порядок делителя, а мантиссу
делимого разделить на мантиссу делителя.
Результатами выполнения операций умножения и деления нормализованных чисел а и Ь в арифметике с ограниченным числом разрядов будут:
d = а • Ь = (О, та • О, ть) х 2 qa![]()
![]() : Ь = (О, та :
: Ь = (О, та :![]()
Пример 13. Выполним умножение двух вещественных чисел: 0,23000 х 10 3 и 0,95000 х 10 7 .
При умножении двух вещественных чисел в представлении с плавающей запятой порядки складываются, а мантиссы перемножаются. В результате получим: 0,21850 х 10 10 . Это число не умещается в отведенный формат — в нашем формате под порядок отводится один разряд, а в получившемся числе порядок содержит две цифры. Выполнение операции умножения над этими числами приведет к прекращению выполнения программы в связи с ошибкой «переполнение порядка».
При делении вещественных чисел в представлении с плавающей запятой порядки вычитаются, а мантиссы делятся одна на другую. В нашем примере при делении мантисс мы имеем бесконечную периодическую дробь 0,92:0,3 — 3,0(6). Следовательно, при записи мантиссы результата произойдет ее округление. После нормализа-
-2 ции результат будет иметь вид:
0,30667 х 10![]()
2.2,4. Особенности реализации вещественной компьютерной арифметики
Когда говорят о точности представления вещественных чисел в
компьютере, надо помнить следующее: десятичное число, имеющее даже всего одну
значащую цифру после запятой, вообще говоря, невозможно представить точно в
формате с плавающей запятой. Объясняется это тем, что конечные десятичные дроби
часто оказываются бесконечными периодическими двоичными дробями. Так 0,110 — ![]() а
значит, и в нормализованном виде такое двоичное число будет иметь бесконечную
мантиссу и не может быть представлено точно. При записи подобной мантиссы в
ячейку компьютера число не усекается, а округляется. Если под мантиссу отведено
п разрядов и (п+1)-я значащая цифра двоичной нормализованной мантиссы равна О,
то цифры, начиная с (п+1)-й, просто отбрасываются, если же (п+1)-я цифра равна
единице, то к целому числу, составленному из первых п значащих цифр мантиссы,
прибавляется единица.
а
значит, и в нормализованном виде такое двоичное число будет иметь бесконечную
мантиссу и не может быть представлено точно. При записи подобной мантиссы в
ячейку компьютера число не усекается, а округляется. Если под мантиссу отведено
п разрядов и (п+1)-я значащая цифра двоичной нормализованной мантиссы равна О,
то цифры, начиная с (п+1)-й, просто отбрасываются, если же (п+1)-я цифра равна
единице, то к целому числу, составленному из первых п значащих цифр мантиссы,
прибавляется единица.
Пример 15. Рассмотрим, как будет выглядеть запись мантиссы (т) числа а = 0,110 при двоичной нормализации для различного количества бит (п), отведенных под мантиссу.
а = 0,110 ![]() х 2 -3 , т. е. мантисса в нормализованном
числе есть 0,11(0011)
х 2 -3 , т. е. мантисса в нормализованном
числе есть 0,11(0011) ![]()
При п = 10 т = 1100110011 (остальные цифры мантиссы отброшены в результате округления).
При п = 12 т = 110011001101 (последняя цифра изменилась с О на 1 при округлении).
Опишем ситуации, приводящие к неточности вычислений, которые могут возникнуть при операциях сложения и вычитания в вещественной компьютерной арифметике.
1. Потеря значащих цифр мантиссы у меньшего из чисел при выравнивании порядков
При сложении и вычитании вещественных чисел в худшем случае утерянными оказываются все значащие цифры меньшего числа, и а + Ь а, что является абсурдным с точки зрения математики, но возможным в компьютерной арифметике с ограниченным числом разрядов (см. пример 12).
2. Потеря крайней справа значащей цифры результата при сложении или вычитании
При сложении и вычитании двух чисел количество значащих цифр может увеличиться лишь на одну, это влияет на точность, но не на правильность результата.
Пример 16. При сложении пятнадцатиразрядных мантисс
![]()
количество значащих цифр стало равным 16, и после
округления и нормализации результат будет выглядеть так: 0,110001010100010 х 2 1![]()
Гораздо хуже обстоит дело при вычитании близких по модулю и имеющих одинаковый знак чисел (или сложении чисел разного знака). В этом случае достоверной может остаться всего одна значащая цифра, а остальные цифры нормализованной мантиссы (скорее всего нули) окажутся недостоверными.
Пример 17. Пусть требуется вычислить
разность чисел ![]() и 0,001100110011
и 0,001100110011 ![]()
Произведем
вначале вычитание «на бумаге». Представим первую дробь (она периодическая) в
виде ![]() Перед периодом выписали 12 цифр, так как
вторая дробь содержит 12 значащих цифр. Произведем вычитание и получим:
Перед периодом выписали 12 цифр, так как
вторая дробь содержит 12 значащих цифр. Произведем вычитание и получим:
-14
![]()
конечно убывающей геометрической прогрессии с q![]()
2
11002
![]() 0,0011001100112
0,0011001100112 ![]() 24
24
![]()
При выполнении этой же операции вычитания в компьютере при условии, что под мантиссу отведено 12 разрядов, получим: 0,1100110011012 х 2-2 - 0,11001100112
-2 -13 ![]()
![]() 0,12 х 2 1 х 2
0,12 х 2 1 х 2
![]()
т. е. уже старшая значащая цифра результата оказалась неверной. 2
З. Выход за границу допустимого диапазона значений при нормализации результата
Данная ситуация возникает в случае,
когда порядок результата оказывается либо больше максимально воз![]() можного
значения, либо меньше минимально возможного. Такую ситуацию различные
компиляторы и операционные системы обрабатывают по-разному, но чаще всего
выполнение программы прерывается с сообщением об ошибке «арифметическое
переполнение» .
можного
значения, либо меньше минимально возможного. Такую ситуацию различные
компиляторы и операционные системы обрабатывают по-разному, но чаще всего
выполнение программы прерывается с сообщением об ошибке «арифметическое
переполнение» .
Пример 18. Выполним сложение
![]() 128
и если максимальный представимый порядок равен 127, результат оказывается не
представимым.
128
и если максимальный представимый порядок равен 127, результат оказывается не
представимым.
Опишем ситуации, приводящие к неточности вычислений при выполнении умножения; деления вещественных чисел.
4. Получение «не представимого»
Данная ситуация соответствует описанному выше «арифметическому переполнению»; однако в 80-разрядном представлении вещественных чисел (а именно он является основным в современных персональных компьютерах) диапазон допустимых порядков достаточно велик, чтобы производить практические любые вычислительные работы, и возникновение подобной ошибки скорее всего означает, что программа составлена неверно.
5, Потеря младших значащих цифр результата
Во-вторых, при операции умножения возможна потеря п-й младшей значащей цифры результата при сдвиге мантиссы на один разряд влево. Самый правый разряд мантиссы при этом заполняется нулем, а не очередной значащей цифрой результата перемножения мантисс, с одновременным уменьшением порядка результата на единицу. Для операции же деления может понадобиться сдвиг вправо вместе с увеличением порядка результата на единицу.
Таким образом, у вещественной арифметики есть несколько потенциально опасных особенностей. Все они имеют общее происхождение, а именно, тот факт, что мантисса и порядок в представлении с плавающей запятой занимают фиксированное число разрядов.
Подведем итог всему сказанному о компьютерной вещественной арифметике:
а) уже на стадии записи чисел в компьютер возникают ошибки округления, которые при выполнении арифметических действий нарастают;
б) наличие погрешностей округления приводит к следующему правилу программирования: неразумно сравнивать в программе два вещественных числа на точное равенство (вместо сравнения на равенство правильнее требовать, чтобы модуль разности сравниваемых чисел не превосходил некоторого числа г, соответствующего абсолютной погрешности представления);
в) в результате вычитания возникают недостоверные значащие цифры, которые могут привести к серьезной потере точности или получению неправильного результата;
г) прибавление или вычитание малого числа может никак не сказаться на результате;
д) получение очень больших чисел может вызвать переполнение порядка, а очень малых отрицательное переполнение, или исчезновение числа (превращение в нуль), это может привести к аварийному завершенико программы.
Вопросы и задания
1.
а) 217,934; в) 10,0101; 6) 75321; г) 0,00200450.
2. Приведите к нормализованному виду следующие числа, используя в качестве Р основания их систем счисления:
а) -0,0000010111012; 6) 98765432101$
в) 123456789,ABCD16![]()
З. Сравните следующие числа:
![]() а) 318,4785 х 10 9
и 3,184785 х 10 11 6) 218,4785 х 10-3 и 21847,85 х 10
а) 318,4785 х 10 9
и 3,184785 х 10 11 6) 218,4785 х 10-3 и 21847,85 х 10
в) 0,11012 х 2 2 и 1012 х 2-2![]()
4. Сравните диапазон представления чисел с плавающей запятой в 32-разрядном формате (24 разряда для мантиссы и 6 разрядов для модуля порядка) с диапазоном представления чисел с фиксированной запятой в том же формате.
5. Каковы преимущества компьютерного представления чисел с плавающей запятой по сравнению с их представлением с фиксированной запятой, которое мы чаще всего используем в повседневной жизни?
6. Произведите следующие арифметические действия над десятичными нормализованными числами согласно правилам вещественной компьютерной арифметики (в мантиссе должно быть сохранено 6 значащих цифр)1.
а) 0,397621 х 10 3 + 0,237900 х 10 [2] , 6) 0,982563 х 10 2 0,745623 х 10 2 ; в) 0,235001 х 10 2 • 0,850000 х 10 3 ;
г) 0,117800 х 10 2 • 0,235600 х 10 3 .
7. Выполните действие над машинными кодами чисел с плавающей запятой в 32-разрядном формате (см. задание 4): Х = А + В, где А = 125,75 и В = —50.
8. Перечислите и объясните все ошибки, которые могут возникать при арифметических операциях с нормализованными числами в ограниченном числе разрядов.
9.
10. Подберите такие значения вещественных чисел а, Ь и с, чтобы при вычислениях на описанном выше школьном калькуляторе значение результата зависело от порядка суммирования, т. е. а + Ь + с * с + Ь + а.
S 2,3, Представление текстовой информации
Всякий текст состоит из символов — букв, цифр, знаков препинания и т. д., которые человек различает по начертанию. Однако для компьютерного представления текстовой информации такой метод неудобен, а для компьютерной обработки текстов и вовсе неприемлем.
Пример 19. Пусть в компьютере сохранены изображения двух похожих слов («караван» и «каравай»):
КАРАВАН КараваЙ
Чтобы расположить эти слова в алфавитном порядке, компьютер должен проанализировать, из каких букв состоят слова и в какой последовательности расположены буквы в словах. Но одинаковые буквы изображены на двух картинках по-разному. Эта задача, как и задача нахождения общей части этих двух слов, неразрешима в таком представлении. Действительно, общая часть этих слов должна быть изображением текста «карава». Но поскольку исходные слова записаны по-разному, то соответствующие части изображений тоже выглядят по-разному. А это значит, что если мы выберем изображение текста «карава» из первой картинки, то оно не будет совпадать с соответствующей частью второго изображения.
Все кодовые таблицы, используемые в любых компьютерах и любых операционных системах, подчиняются международным стандартам кодирования символов. На заре компьютерной эпохи, когда США были абсолютным лидером в этой области, стандарты разрабатывались Американским национальным институтом стандартизации (ANSI); впоследствии для разработки и принятия КОМПЬютерных стандартов была создана Международная организация стандартизации (ISO).
В программировании наиболее часто используются однобайтовые кодировки: в них код каждого символа занимает ровно 1 байт, или 8 бит. При этом общее количество различаемых символов составляет 2 8 = 256, а коды символов имеют значения от О до 255.
Определение 7. Информационным объемом блока информации называется количество бит, байт или производных единиц (килобайт, мегабайт и т. д.), необходимых для записи этого блока путем заранее оговоренного способа двоичного кодирования.
Задание. Оцените в байтах объем текстовой информации в «Современном словаре иностранных слов» из 740 страниц, если на одной странице размещается в среднем 60 строк по 80 символов (включая пробелы).
Решение. Будем считать, что при записи
используется кодировка «один символ — один байт» . Количество символов во всем
словаре равно 80 • 60 • 740 = З 552 ООО. Следовательно, объем в байтах равен З
552 ООО байт = З 468,75 Кбайт ![]()
![]() 3,39 Мбайт.
3,39 Мбайт.
например:
|
Код |
Действие |
|
Английское название |
|
7 |
Подача стандартного звукового сигнала |
|
|
|
8 |
Удаление предыдущего символа |
|
ВасК space (BS) |
|
13 |
Перевод строки |
|
Line Feed (LF) |
|
26 |
Признак «Конец текстового файла» |
|
End Of File (EOF) |
|
27 |
Отмена предыдущего ввода |
|
Escape (Esc) |
К изображаемым символам в ASCII
относятся буквы английского алфавита (прописные и строчные), цифры, знаки
препинания и арифметических операций, скобки и некоторые специальные символы.
Фрагмент кодировки ASCII приведен в табл. 1. ![]()
Таблица 1
|
Символ |
Десятичный код |
Двоичный код |
Символ |
Десятичный код |
Двоичный код |
|
Пробел |
32 |
00100000 |
|
48 |
00110000 |
|
|
33 |
00100001 |
1 |
49 |
00110001 |
|
|
35 |
00100011 |
2 |
50 |
00110010 |
|
|
36 |
00100100 |
з |
51 |
00110011 |
|
|
42 |
00101010 |
4 |
52 |
00110100 |
|
|
|
00101011 |
5 |
53 |
00110101 |
|
|
44 |
00101100 |
6 |
54 |
00110110 |
|
|
45 |
00101101 |
7 |
55 |
00110111 |
|
|
46 |
00101110 |
8 9 |
56 |
00111000 00111001 |
|
в |
47 65 |
01000001 |
о |
57 78 79 |
01001110 |
|
с |
66 67 |
01000010 01000011 |
|
80 |
01010000 |
|
|
68 |
01000100 |
|
81 |
01010001 |
|
|
69 |
01000101 |
|
82 |
01010010 |
|
|
70 |
01000110 |
|
83 |
01010011 |
|
|
71 |
01000111 |
т |
|
01010100 |
|
н |
72 |
01001000 |
|
85 |
01010101 |
|
|
73 |
01001001 |
|
86 |
01010110 |
|
|
74 |
01001010 |
|
87 |
01010111 |
|
|
75 |
01001011 |
х |
88 |
01011000 |
|
1, |
76 |
01001100 |
|
89 |
01011001 |
|
м |
77 |
01001101 |
|
90 |
01011010 |
Хотя в ASCII символы кодируются 7 битами, в памяти компьютера под каждый символ отводится ровно 1 байт, при этом код символа помещается в младшие биты, а старший бит не используется.
Главный недостаток стандарта ASCII заключается в том, что он рассчитан на передачу только английского текста. Со временем возникла необходимость кодирования и неанглийских букв. Во многих странах для этого стали разрабатывать расширения ASCII-tcoTl.pomcu, в которых применялись однобайтовые коды символов; при этом первые 128 символов кодовой таблицы совпадали с кодировкой ASCII, а остальные (со 128-го по 255-й) использовались для кодирования букв национального алфавита, символов национальной валюты и т. п. Из-за несогласованности этих разработок для многих языков было создано по нескольку вариантов кодовых таблиц (например, для русского языка их около десятка!).
Впоследствии использование кодовых таблиц было несколько упорядочено: каждой кодовой таблице было присвоено особое название и номер. Указав кодовую таблицу, автоматически выбирают и язык, которым можно пользоваться в дополнение к английскому; точнее, выбирается то, как будут интерпретироваться символы с кодами более 127.
Таблица 2
Кодировка КОИ-8
![]()
1 Иначе эта кодировка обозначается сокращением СР-1251 (Code Page — кодовая страница).
Таблица З
Пример 20. Вот так будет выглядеть десятичный код слова «Диск» в разных кодировках:
кои-8 228 201 211 203 Windows—1251 196 232 241 234
СР-866 132 168 225 170
Однобайтовые кодировки обладают одним серьезным ограничением: количество различных кодов символов в этих кодировках недостаточно велико, чтобы можно было пользоваться одновременно несколькими языками. Для устранения этого ограничения в 1993 году был разработан новый стандарт кодирования символов, получивший название Unicode, который, по замыслу его разработчиков, позволил бы использовать в текстах любые символы любых языков мира.
![]() В Unicode на
кодирование символов отводится 31 бит. Первые 128 символов (коды 0—127)
совпадают с таблицей ASCII; далее размещены основные алфавиты современных
языков: они полностью умещаются в первой части таблицы, их коды не превосходят
65 536 (65 536 = 2 16 ). А в целом стандарт Unicode описывает
алфавиты всех известных, в том числе и «мертвых», языков; для языков, имеющих
несколько алфавитов или вариантов написания (например, японский и индийский),
закодированы все варианты; в кодировку Unicode внесены все математические и
иные научные символьные обозначения и даже некоторые придуманные языки
(например, письменности эльфов и Мордора из эпических произведений Дж. Р. Р.
Толкиена). Потенциальная информационная емкость 31-битового Unicode столь
велика, что сейчас используется менее одной тысячной части возможных кодов
символов!
В Unicode на
кодирование символов отводится 31 бит. Первые 128 символов (коды 0—127)
совпадают с таблицей ASCII; далее размещены основные алфавиты современных
языков: они полностью умещаются в первой части таблицы, их коды не превосходят
65 536 (65 536 = 2 16 ). А в целом стандарт Unicode описывает
алфавиты всех известных, в том числе и «мертвых», языков; для языков, имеющих
несколько алфавитов или вариантов написания (например, японский и индийский),
закодированы все варианты; в кодировку Unicode внесены все математические и
иные научные символьные обозначения и даже некоторые придуманные языки
(например, письменности эльфов и Мордора из эпических произведений Дж. Р. Р.
Толкиена). Потенциальная информационная емкость 31-битового Unicode столь
велика, что сейчас используется менее одной тысячной части возможных кодов
символов!
Вопросы и задания
1. На чем основывается возможность двоичного кодирования текстовой информации?
2. На основании чего можно утверждать, что для латинских букв применяется семибитовое кодирование?
З. Зная, что в кодировке ASCII десятичный код каждой строчной латинской буквы на 32 больше кода соответствующей прописной буквы, представьте фрагмент этой кодировочной таблицы в формате, основанном на шестнадцатеричной системе счисления:
|
|
0 1 2 3 4 5 6 7 8 9 A B C I) E F |
|
||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4. Используя результат выполнения предыдущего задания, декодируйте следующее сообщение, записанное в восьмибитовой кодировке:
01010101 01110000 00100000 00100110 00100000
![]()
5. Определите вид кодировки и декодируйте следующие сообщения:
а) 235 207 212 197 204 216 206 201 203 207 215; 6) 213 224 244 244 236 224 237.
6. Петя и Коля пишут друг другу электронные письма. Однажды Петя отправил Коле письмо в кодировке Windows-1251 , Коля письмо получил, но прочитал его в кодировке КОИ-8. Получился бессмысленный текст, одно из предложений которого имело вид:
КЧАЮЪ ХМТНплЮЖХЪ ЛНФЕР АШРЭ
ОПЕДЯРЮБЕЕМЮ Я ОНЛНЫЭЧ ВХЯњю
Какое предложение было в исходном сообщении?
7.
8. Будут ли
упорядочены по алфавиту фамилии, записанные русскими буквами, если их
сортировку осуществить ![]() согласно кодам символов из кодировки
Windows- 1251 ?
согласно кодам символов из кодировки
Windows- 1251 ?
9. Почему в кодировке ASCII сдвиг, с помощью которого по коду прописной английской буквы можно получить код соответствующей строчной, равен 32, а не, например, 26 (в кодировках КОИ-8 и Windows-1251 это же свойство сохраняется и для русских букв)?
S 2,4. Представление графической информации
Подавляющую часть информации об окружающем мире человек получает с помощью зрения — по оценкам ученых, доля зрительной информации составляет не менее 80 0/0 общего потока информации, воспринимаемого всеми органами чувств. Важность зрения обусловлена историческим развитием человека как биологического вида, поэтому зрительные органы человека, и особенно зрительные центры мозга, прекрасно приспособлены к обработке информации с большой скоростью и в больших объемах. С появлением компьютеров, способных быстро обрабатывать информацию, и их совершенствованием ученые стали разрабатывать компьютерные методы хранения и обработки изображений.
2.4.1 . Общие подходы к представлению в компьютере информации естественного происхождения
Для преобразования «естественной»
информации в дискретную форму ее подвергают Дискретизации и квантованию.![]()
Определение 8. Дискретизацией (англ. discretisation) называют процедуру устранения временнбй и/или пространственной непрерывности естественных сигналов, являющихся носителями информации.
При пространственной Дискретизации изображения его разбивают на небольшие области, в пределах которых характеристики изображения считают неизменными.
Пример 21. Пространственная дискретизация изображения.
При временнбй Дискретизации время разбивают на небольшие интервалы, в пределах которых характеристики природных сигналов, как и в пространственном случае, считают неизменными.
Наглядным примером временнбй дискретизации могут служить кино и телевидение. В них иллюзия подвижного изображения создается путем быстрой смены кадров. При этом сами кадры являются статическими изображениями. Компьютерное кодирование видеоинформации также основано на эффекте смены кадров, на которых изображены последовательные фазы движения.

Пример 23. Временнбя дискретизация звукового сигнала.
Вопрос. Зачем нужна Дискретизация изображения?
Ответ. Пространство непрерывно, а это означает, что в любой его области содержится бесконечное количество точек. Если мы хотим точно сохранить изображеНИе, то должны запоминать информацию о каждой точке пространства (если мы какие-то точки не учитываем, то не сможем различить два изображения, которые отличаются друг от друга только в этих точках).
Поскольку точек бесконечно много, то и компьютерное представление должно было бы содержать бесконечно много информации, и для его сохранения потребовалось бы бесконечное количество памяти. А это значит, компьютеры в принципе не могли бы ни обрабатывать, ни хранить подобные изображения! Чтобы компьютер мог работать с изображениями, необходимо ограничиться запоминанием конечного количества объектов пространства (точек или областей). Дискретизация и есть способ выделения конечного числа пространственных элементов, информация о которых будет сохранена в компьютере. Информация обо всех остальных элементах пространства при дискретизации
утрачивается!
С информационной точки зрения графическое изображение является совокупностью световых сигналов на плоскости: отдельные световые сигналы различаются местоположением, цветовым оттенком и яркостью.
Определение 9. Квантованием (англ. quantisation или quantization) называют процедуру преобразования непрерывного диапазона всех возможных входных значений измеряемой величины в дискретный набор выходных значений.
Обычно при квантовании диапазон возможных значений измеряемой величины разбивается на несколько поддиапазонов. При измерении определяется поддиапазон, в который попадает значение, и в компьютере сохраняется только номер поддиапазона.
Пример 24. Квантование шкалы оттенков серого цвета.
![]() В
правой части рисунка изображена шкала градаций серого цвета, от черного до
белого. Для численного описания яркости цвета надо каждому оттенку поставить в
соответствие некое число. Как правило, черному цвету приписывают нулевой
уровень яркости, белому единичный, а промежуточным серым тонам — дробные
числа в интервале от О до 1, выраэкающие яркость оттенка как долю от
максимальной яркости. Эту величину мы будем
В
правой части рисунка изображена шкала градаций серого цвета, от черного до
белого. Для численного описания яркости цвета надо каждому оттенку поставить в
соответствие некое число. Как правило, черному цвету приписывают нулевой
уровень яркости, белому единичный, а промежуточным серым тонам — дробные
числа в интервале от О до 1, выраэкающие яркость оттенка как долю от
максимальной яркости. Эту величину мы будем
шкала шкала
выражать в процентах от
максимальной яркости, т. е. черный имеет 0 0/0 яркости, белый 100 0/0 .
![]() Такое описание цвета
непригодно для непосредственного компьютерного представления, так как
вещественные числа недискретны, для точной записи их значений надо хранить
бесконечное количество цифр! Следовательно, надо провести квантование, для чего
диапазон значений яркости разбивают на поддиапазоны, или уровни. В нашем
примере диапазон яркости серого цвета разбиваем на 6 уровней равной ширины: О-й
уровень — 0—1794 максимальной яркости, 1-й уровень 17—33 0/0
максимальной яркости и т. д. Тогда интервалы значений яркости и номера уровней
связаны друг с другом простым соотношением: К-й уровень соответствует интервалу
Такое описание цвета
непригодно для непосредственного компьютерного представления, так как
вещественные числа недискретны, для точной записи их значений надо хранить
бесконечное количество цифр! Следовательно, надо провести квантование, для чего
диапазон значений яркости разбивают на поддиапазоны, или уровни. В нашем
примере диапазон яркости серого цвета разбиваем на 6 уровней равной ширины: О-й
уровень — 0—1794 максимальной яркости, 1-й уровень 17—33 0/0
максимальной яркости и т. д. Тогда интервалы значений яркости и номера уровней
связаны друг с другом простым соотношением: К-й уровень соответствует интервалу
100 100
к .![]()
6 6
![]()
По величине яркости легко вычислить номер соответствующего уровня: К [х 6/100] (здесь квадратные скобки означают целую часть числа), где х — величина яркости, К — номер уровня.
Пусть яркость серого оттенка составляет 70 0/0 . При
70 420 квантовании = 4 это значение попада-
100 100
ет в 4-й поддиапазон (67—8394 поэтому в компьютере этот оттенок серого будет закодирован целым числом 4.
Дискретизация и квантование всегда приводят к потере некоторой доли информации. Так, компьютерное изображение живописного полотна всегда отличается от оригинала. А цифровая запись музыкального произведения или концерта (например, на компакт-диске) всегда отличается от живого звучания, даже если различие неощутимо на слух. Степень различия оригинала и цифровой копии определяет субъективное качество компьютерного представления.
Из-за больших размеров звуковых, графических и видеофайлов они очень редко хранятся в компьютере в неупакованном виде. Для уменьшения их размеров используют сжатие информации. Универсальные, или так называемые обратимые алгоритмы сжатия, никак не используют знания о характере обрабатываемой информации и поэтому упаковывают ее ДОСТаТОЧно слабо.
Для эффективного сжатия звуковой и графической информации относительно недавно были разработаны специальные алгоритмы, учитывающие специфику человеческого восприятия звука и изображений. Характерной особенностью этих алгоритмов является возможность регулируемого удаления маловажной (с точки зрения человеческого восприятия) информации, поэтому такие алгоритмы сжатия обобщенно называют алгоритмами с регулируемой потерей информации. За счет удаления части информации удается добиться очень большой степени сжатия данных при субъективно незначительной потере качества.
![]() Алгоритмы с регулируемой потерей информации неуниверсальны,
они не могут использоваться для сжатия любых данных, поскольку полное
восстановление исходной информации невозможно.
Алгоритмы с регулируемой потерей информации неуниверсальны,
они не могут использоваться для сжатия любых данных, поскольку полное
восстановление исходной информации невозможно.
При пространственной дискретизации изображений пользуются растровым и векторным представлением графической информации. Растровое представление можно охарактеризовать как поточечное преДставление, а векторное как структурное представление изображения .
2.4.2. Векторное и растровое представление
графической информации
Помните, как вы рисовали в детстве?
Точка, точка, запятая![]()
Вышла рожица кривая. Палка, палка, огуречик ![]() Получился
человечек!
Получился
человечек!
Слова этой детской песенки очень точно характеризуют суть векторного представления графической информации.
Геометрические фигуры из стандартного набора называют элементарными фигурами, или примитивами (англ. primitives). Построение векторного представления называется векторизацией изображения. При выполнении векторизации изображение анализируют, разбивают на примитивы, а затем сохраняют их параметры: положение, размеры и цвет.
Многие виды изображений по своей природе хорошо структурированы и поэтому очень удобны для векторизации: это графики, диаграммы, чертежи, схемы, планы, карты, символы, гербы и флаги, логотипы, всевозможные стилизованные изображения.
Пример 25. Любой чертеж содержит
отрезки, окружности, дуги. Положение каждого отрезка на чертеже можно задать
координатами двух точек, определяющими его начало и конец; окружность
координатами центра и длиной радиуса; дугу — радиусом, а также координатами
начала и конца дуги. Кроме того, для каждой линии ![]() можно указать ее тип:
тонкая, штрихпунктирная и т. д.
можно указать ее тип:
тонкая, штрихпунктирная и т. д.
Такая информация о чертеже вводится в компьютер как обычная буквенно-цифровая и обрабатывается в дальнейшем специальными программами.
В отличие от хорошо структурированных изображений существуют изображения, которые вообще не имеют четкой структуры. К ним относятся фотографии, живописные полотна, рукописные тексты и т. д. Такие изображения крайне неудобны для векторизации.
Для хранения подобных изображений используют растровое представление: все изображение разбивается на множество очень маленьких элементов, причем, в отличие от векторного представления, размеры и положение элементов задаются заранее (а priori) и совершенно не зависят от самого изображения. В пределах каждого такого элемента изображение считается однородным, т. е. имеющим один и тот же цвет.
Заметим, что хранение рисунка в векторной форме обычно на несколько порядков сокращает необходимый объем памяти по сравнению с растровой формой представления.
Определение 10. Растр — специальным образом организованная совокупность пикселей, представляющая изображение. Координаты, форма и размер пикселей задаются при определении растра. Изменяемым атрибутом пикселей является цвет.
В технике и компьютерной графике чаще всего используется прямоугольный растр, в котором пиксели составляют прямоугольную матрицу, ее основными параметрами являются размеры растровой матрицы, т. е. количество столбцов и строк, составленных из пикселей.
Главное преимущество прямоугольных
растров за![]() ключается в том, что положение каждого
пикселя на экране (или на изображении) можно вычислить, зная только размеры
растровой матрицы и линейные размеры пикселей либо плотность размещения
пикселей, которую обычно измеряют в количестве точек на дюйм (dpi, Dots Per
Inch). Для этого достаточно ввести правила перечисления пикселей. Например, в
мониторах персональных компьютеров пиксели перечисляются слева направо и сверху
вниз: сперва нумеруются все пиксели в верхней строке слева направо, затем
нумерация продолжается на нижележащей строке и т. д.
ключается в том, что положение каждого
пикселя на экране (или на изображении) можно вычислить, зная только размеры
растровой матрицы и линейные размеры пикселей либо плотность размещения
пикселей, которую обычно измеряют в количестве точек на дюйм (dpi, Dots Per
Inch). Для этого достаточно ввести правила перечисления пикселей. Например, в
мониторах персональных компьютеров пиксели перечисляются слева направо и сверху
вниз: сперва нумеруются все пиксели в верхней строке слева направо, затем
нумерация продолжается на нижележащей строке и т. д.
х
 1023 (1023,0)
1023 (1023,0)
(0, 767) (1023,767)
2.4.3. Квантование цвета
Как было сказано выше, графическую информацию естественного происхождения при вводе в компьютер необходимо подвергать операциям пространственной дискретизации и квантования цвета.
Квантование (кодирование) цвета базируется на математическом описании цвета, которое, в свою очередь, опирается на тот факт, что цвета можно измерять и сравнивать. Научная дисциплина, изучающая вопросы измерения цветовых характеристик, называется метрологией цвета, или колориметрией. Человек обладает очень сложным цветовосприятием, достаточно заметить, что зрительные центры мозга у новорожденных детей в течение нескольких месяцев (!) только тренируются видеть. Поэтому и математическое описание цвета тоже весьма нетривиально.
Ученым долгое время не удавалось объяснить процесс цветовосприятия. До середины XVII века господствовала умозрительная теория Аристотеля, согласно которой все цвета образуются при подмешивании черного цвета к бе-
лому.
![]() Примерно полстолетия
спустя, в 1756 году, выдающийся русский ученый М. В. Ломоносов сформулировал
так называемую трехкомпонентную теорию цвета, обобщив огромный эмпирический
материал, накопленный им при разработке технологии производства цветного стекла
и мозаики. Исследуя вопросы окрашивания стекол, Ломоносов обнаружил, что для придания
стеклу любого
Примерно полстолетия
спустя, в 1756 году, выдающийся русский ученый М. В. Ломоносов сформулировал
так называемую трехкомпонентную теорию цвета, обобщив огромный эмпирический
материал, накопленный им при разработке технологии производства цветного стекла
и мозаики. Исследуя вопросы окрашивания стекол, Ломоносов обнаружил, что для придания
стеклу любого
|
М. В. Ломоносов |
цветового оттенка достаточно использо- |
|
(1711-1765) |
вать всего три основные краски, смеши- |
вая их в определенных пропорциях.
Спустя примерно столетие выдающийся немецкий ученый Герман Грассман (1809—1877) ввел в трехкомпонентную теорию цвета математический аппарат в форме законов Грассмана для аддитивного синтеза цвета. Наиболее важными из них являются следующие два закона.
Закон трехмерности: с помощью трех линейно независимых цветов можно однозначно выразить любой цвет. Цвета считаются линейно независимыми, если никакой из них нельзя получить путем смешения остальных.
Закон непрерывности: при непрерывном изменении состава цветовой смеси результирующий цвет также меняется непрерывно. К любому цвету можно подобрать бесконечно близкий цвет.
Трехкомпонентная теория цвета стала основой колориметрии, однако обоснование этой теории появилось только на рубеже XIX—XX веков, после того, как была изучена физиология органов зрения,
Таким образом, цвета можно рассматривать как точки или векторы в трехмерном цветовом пространстве. Каждая цветовая модель задает в нем некоторую систему координат, в которой основные цвета модели играют роль базисных векторов. А квантование цвета, по сути, является дискретизацией пространства цветов.
В компьютерной технике чаще всего используются следующие цветовые модели:
![]() RGB
RGB ![]() красный—зеленый—синий).
красный—зеленый—синий). ![]() СМУ К (Cyan—Magenta—Yellow—black, голубой—пурпурный—желтый—черный).
СМУ К (Cyan—Magenta—Yellow—black, голубой—пурпурный—желтый—черный).
• HSB (Hue—Saturation—Brightness, цветовой оттенок—насыщенность—яркость).
Чтобы исключить неоднозначность трактования терминов «яркость», «насыщенность», «цветовой оттенок», поясним их.
Яркость это характеристика цвета,
определение ![]() которой в основном совпадает с бытовым
понятием ярко
которой в основном совпадает с бытовым
понятием ярко![]() сти и физическим понятием освещенности или
светимости. Ярко-красный, красный и темно-красный цвета различаются именно
яркостью.
сти и физическим понятием освещенности или
светимости. Ярко-красный, красный и темно-красный цвета различаются именно
яркостью.
![]() С физической точки
зрения, яркость — это количественная мера потока световой энергии, излучаемой
или отражаемой предметом в сторону наблюдателя. Так, при ярком солнечном свете
и в сумерках один и тот же цветной рисунок выглядит по-разному. При этом
цветовые оттенки не меняются, различными оказываются лишь яркости цветов.
С физической точки
зрения, яркость — это количественная мера потока световой энергии, излучаемой
или отражаемой предметом в сторону наблюдателя. Так, при ярком солнечном свете
и в сумерках один и тот же цветной рисунок выглядит по-разному. При этом
цветовые оттенки не меняются, различными оказываются лишь яркости цветов.
Цветовой оттенок и насыщенность — это две другие независимые характеристики цвета.
Насыщенность характеризует степень
«разбавления» цветового тона белым цветом. Например, если яркокрасную
(насыщенную) краску разбавить белой, то ее цветовой оттенок останется прежним,
изменится только насыщенность. Ровно так же коричневый цвет, желтый и лимонный
имеют один и тот же цветовой оттенок ![]() желтый, их различие заключается в
насыщенности цветового оттенка. Наибольшей насыщенностью обладает свет от
монохромного источника.
желтый, их различие заключается в
насыщенности цветового оттенка. Наибольшей насыщенностью обладает свет от
монохромного источника.
Отметим, что для белого и черного цветов
насыщенность составляет 0 0/0 , т. е. эти цвета не обладают
насыщенностью. Именно поэтому, подмешивая их к цветной ![]() краске, мы меняем ее
насыщенность, а не оттенок.
краске, мы меняем ее
насыщенность, а не оттенок.
2.4,4. Цветовая модель RGB
В модели RGB основными цветами являются красный, зеленый и синий. Данная модель используется в основном при отображении графических изображений на экране монитора, телевизора, сотового телефона и т. д. Смешением трех основных цветов синтезируются все остальные цвета, их условные яркости (интенсивности) задаются вещественными числами от О до 1 (значение 1 соответствует максимальной яркости соответствующего цвета, которую может изобразить графическое устройство). Модель RGB определяет пространство цветов в виде единичного куба с осями «яркость красной компоненты», «яркость зеленой компоненты» и «яркость синей компоненты ».
голубой белый
черный красный
Характерные особенности RGB-M0l3eJIli
![]() Любая точка куба
(р, g, Ь) определяет некоторый цвет.
Любая точка куба
(р, g, Ь) определяет некоторый цвет.
![]() Точка (О, О, О)
соответствует черному цвету, точка
Точка (О, О, О)
соответствует черному цвету, точка ![]() белому, а линия (0, 0, 0) — (1, 1, 1)
описывает
белому, а линия (0, 0, 0) — (1, 1, 1)
описывает
все градации серого цвета: от черного до белого.
![]() При движении по
прямой от (О, О, О) через точку (r, g, Ь) получаем все градации яркости цвета
{r, g, Ь), от самой темной до самой яркой. Например, ( 1 /4, 1 /4,
О) — темнокоричневый цвет, ( 1 /2, 1 /2, О) — коричневый,
( 3 /4 , 3 /4, О) — желто-коричневый, (1, 1, О) — желтый.
При движении по
прямой от (О, О, О) через точку (r, g, Ь) получаем все градации яркости цвета
{r, g, Ь), от самой темной до самой яркой. Например, ( 1 /4, 1 /4,
О) — темнокоричневый цвет, ( 1 /2, 1 /2, О) — коричневый,
( 3 /4 , 3 /4, О) — желто-коричневый, (1, 1, О) — желтый.
![]() На гранях куба {r
= 0}, {g = 0} и {b = 0} расположены са-
На гранях куба {r
= 0}, {g = 0} и {b = 0} расположены са-
мые насыщенные цвета.
![]() Чем ближе точка к
главной диагонали (0, О, 0) — (1, 1, 1), тем менее насыщен соответствующий
цвет.
Чем ближе точка к
главной диагонали (0, О, 0) — (1, 1, 1), тем менее насыщен соответствующий
цвет.
У цветовой модели RGB есть физиологическое обоснование. Человеческий глаз содержит четыре типа зрительных рецепторов: «палочки» (рецепторы интенсивности) и три типа «колбочек» (рецепторы цветовых оттенков). Колбочки каждого типа чувствительны к свету в своем узком диапазоне длин волн, для колбочек разных типов максимумы чувствительности приходятся на разные длины волн, диапазоны чувствительности частично перекрываются:
Относительная спектральная чувствительность
|
|
|
Именно благодаря неравномерной спектральной чувствительности и перекрытию диапазонов чувствительности человеческий глаз способен различать огромное количество цветов (около 10 млн).
Если направить в глаз составной световой сигнал с правильно подобранным соотношением яркостей красного, зеленого и синего цветов, то зрительные центры мозга не смогут отличить подмену и сделают вывод, что наблюдается нужный цвет! Такой механизм синтеза цветовых оттенков используется во всех современных типах цветных мониторов, телевизоров, дисплеев сотовых телефонов.
Чтобы использовать математическую RGB-M0№JIb для реального компьютерного представления графической информации, необходимо произвести квантование цветового пространства, т. е. найти способ представлять вещественные значения яркостей цветовых компонент в дискретной форме.
Наиболее простой способ добиться этого перевести вещественные числа из интервала [О; 1) в интервал целых чисел от О до N— 1 путем умножения на целое число N, с последующим округлением. Фактически, интервал [О; 1) разбивается на равных подинтервалов вида:
![]()
![]() Разбиению на
подинтервалы подвергают каждую из цветовых осей. Количество подинтервалов на
«красной», «зеленой» и «синей» осях (N , N , Nb) может
Разбиению на
подинтервалы подвергают каждую из цветовых осей. Количество подинтервалов на
«красной», «зеленой» и «синей» осях (N , N , Nb) может ![]() быть различным, но
чаще принимается, что ДГ = N = = N.
быть различным, но
чаще принимается, что ДГ = N = = N.
а величину М, равную сумме т + т + ть, называют глубиной цвета или глубиной цветности.
Ниже приведена таблица наиболее распространенных видеорежимов с указанием количества отображаемых цветов (табл. 4).
Таблица 4
|
Видеорежим |
Глубина цвета |
Количество отображаемых цветов |
|
256 цветов |
8 |
28 - 256 |
|
High Color |
16 |
2 16 = 65 536 |
|
True Color |
24 |
2 24 - 16 777 216 |
Пример 26. В современных компьютерах в видеорежиме TrueColor на хранение информации об одной цветовой компоненте используется 1 байт, для сохранения цвета точки — З байта: mr= m = ть = 8, лт = = N = 2 8 = 256,
8+8+8
![]() 16 777 216.
16 777 216.
Глубины цветности 24 бита для мониторов вполне достаточно, чтобы создать видимость непрерывности шкалы цветовых оттенков. Особенности человеческого зрения таковы, что если на экране монитора изобразить две фигуры, цвета КОТОРЫХ при глубине цвета 24 бита отличаются не более чем на 1 в каждой цветовой компоненте, то человек не сможет заметить разницу.
В табл. 5 для стандарта 1'rueColor приведены двоичные значения уровней интенсивности некоторых цветов.
|
Название цвета |
Интенсивность основных цветов |
||
|
Красный |
Зеленый |
Синий |
|
|
черный |
00000000 |
00000000 |
00000000 |
|
красный зеленый |
00000000 |
00000000
|
00000000 00000000 |
|
синий голубой |
00000000 00000000 |
00000000 |
|
|
пурпурный |
|
00000000 |
00000000 |
|
желтый белый |
|
|
|
Пример 27. В видеорежиме HighColor цвет каждой точки кодируется 16 битами. На глубину красного и синего цвета отводится 5 бит, на глубину зеленого 6 бит: т = т = 5, т = 6. Следовательно, шкала яркостей зеленого цвета содержит в два раза больше уровней, чем шкалы яркостей красного и синего цветов. Для экономии памяти биты цветовых компонент каждой точки записывают в два байта вместо трех,
Задание. Подсчитайте объем памяти, требуемый для сохранения изображения всего экрана для виДеорежима с размером экрана 1024 х 768 пикселей и с глубиной цвета 24 бита.
Решение. Экран монитора представляет
собой прямоугольный растр, поэтому суммарное количество пикселей равно 1024 х
768 - 786 432 пикселей. ![]()
Для видеорежима с глубиной цвета 24 бита требуется З байта на каждый пиксель, так что общий объем требуемой памяти составит 1024 768 • З 2 359 296 байт = 2,25 Мбайт.
Для непосредственной цифровой записи 1
секунды цветного видеоизображения без звука (25 кадров размером 1024 х 768
пикселей) потребуется примерно 60 Мб ![]() = 58 982 400 байт).
Для записи двухчасового фильма необходимо около 400 Гб.
= 58 982 400 байт).
Для записи двухчасового фильма необходимо около 400 Гб.
2.4.5. Цветовая модель СМУК
Цветовая модель СМУК также базируется на
трехкомпонентной теории цвета, но, в отличие от модели RGB, основными цветами в
ней являются голубой, пурпурный и желтый. Модель СМУК широко используется в
цветной печати. Название модели является аббревиатурой английских названий
основных цветов Cyan—Magen![]() ta—Yellow—black. (О причине добавления
черного цвета будет сказано ниже.)
ta—Yellow—black. (О причине добавления
черного цвета будет сказано ниже.)
Главной причиной появления модели СМУК является различие в принципах формирования цвета при его воспроизведении на мониторах и при печати. Кто в детстве рисовал акварельными красками или гуашью, тот знает, что при смешении красной и зеленой красок получается не желтая краска (как было бы в модели RGB), а темно-коричневая. Дело в том, что при восприятии цвета с экрана монитора мы видим излучаемый свет, а при при рассматривании картинки, нарисованной на бумаге, — отраженный.
Пиксели монитора излучают собственный свет; чтобы создать на экране основной цвет, надо включить субэлемент определенного типа (пиксель монитора состоит из трех субэлементов: красного, зеленого и синего), а для получения составного цвета надо дополнительно включить (т. е. Добавить) субэлементы другого типа, при этом суммарная яркость пикселя возрастет. Кстати, из-за такого принципа формирования составного цвета Ж}В-модель называют адДитивной цветовой моДелью (от англ. add — добавлять).
В отличие от монитора, бумага отражает падающий свет, который обычно является «белым»: яркости всех его цветовых составляющих равны. Наносимые на бумагу краски являются поглощающими светофильтрами — они поглощают лучи определенного цвета, а остальные отражают. Видимый цвет краски определяется теми лучами, которые не были поглощены, Таким образом, краски могут только вычитать, или ослаблять цвета в отражаемом потоке света. По этой причине модель СМУК называют субтрактивной цветовой моДелью (от англ. subtract вычитать).
Основные цвета модели СМУК подобраны так, чтобы соответствующие краски поглощали свет в достаточно узкой области спектра: голубая краска сильно поглощает красный свет, пурпурная — зеленый, а желтая — синий.
|
RGB |
|
в |
в |
|
|
Цвет |
Черный |
Красный |
Зеленый |
Синий |
|
|
|
|
|
|
|
RGB |
в |
|
|
|
|
Цвет |
Желтый |
Голубой |
Пурпурный |
Белый |
|
СМУК |
|
|
|
|
В идеальном случае трех цветов (голубого, пурпурного и желтого) было бы вполне достаточно для формирования на бумаге любого цвета. Однако реально существующие краски не идеальны, они не поглощают цветовые компоненты полностью: если нанести на бумагу все три краски с наибольшей плотностью, то вместо чистого черного цвета получится темно-серый. Для коррекции цветовой гаммы используется четвертая краска черная.
Пространство цветов модели СМУК также
является ![]() единичным кубом. Яркости основных красок
(или плотность закраски) задаются вещественными числами от О до 1.
единичным кубом. Яркости основных красок
(или плотность закраски) задаются вещественными числами от О до 1.
С голубой белый
![]()
![]() Линия градаций серого
Линия градаций серого
Линия градаций сине веленого
черный красный
![]()
![]() Любая
точка куба (с, т, у) определяет некоторый цвет.
Любая
точка куба (с, т, у) определяет некоторый цвет.
![]() Точка (О, О, О) соответствует белому
цвету, точка (1, 1, 1) — черному, а линия (О, О, О) — (1, 1, 1) описы
Точка (О, О, О) соответствует белому
цвету, точка (1, 1, 1) — черному, а линия (О, О, О) — (1, 1, 1) описы![]() вает
все градации серого цвета: от белого до черного.
вает
все градации серого цвета: от белого до черного. ![]() При движении по
прямой от (О, О, О) через точку
При движении по
прямой от (О, О, О) через точку
![]() (с, т, у) получаем
все градации яркости цвета {с, т, у), от самой яркой до самой темной,
(с, т, у) получаем
все градации яркости цвета {с, т, у), от самой яркой до самой темной,
![]() Чем
ближе точка к главной диагонали (О, О, О) — (1, 1, 1), тем менее насыщен
соответствующий цвет.
Чем
ближе точка к главной диагонали (О, О, О) — (1, 1, 1), тем менее насыщен
соответствующий цвет. ![]() Если все три координаты точки (с, т, у)
ненулевые, то цвет ненасыщенный.
Если все три координаты точки (с, т, у)
ненулевые, то цвет ненасыщенный.
![]() В
модели СМУК оттенки серого цвета могут воспроизводиться путем добавления черной
краски к основному набору цветов.
В
модели СМУК оттенки серого цвета могут воспроизводиться путем добавления черной
краски к основному набору цветов.
Квантование цвета в модели СМУК выполняется аналогично квантованию в модели RGB.
Как уже упоминалось в п. 2.4.4, цветовая модель RGB соответствует механизму синтеза цветов, используемому в мониторах. А поскольку в современных компьютерах именно мониторы являются главным, наиболее часто используемым устройством вывода информации, то практически все форматы графических файлов хранят изображения в Ж}В-представлении, и лишь очень немногие графические форматы используют другие ЦВетовые модели (например, в формате JPEG используется УТЛТ -модель). Чтобы вывести на экран изображения, хранящиеся в таких графических файлах, программам приходится «на лету» выполнять преобразование графических данных в ЖАВ-представление.
Модель СМУК соответствует механизму
синтеза цветов, используемому в принтерах. Когда графическая информация
выводится на принтер, приходится выполнять преобразование изображения из ![]() ния
в СМУК-представление. Обычно эта работа выполняется средствами ОС, поскольку
формулы пересчета RGB СМУК просты.
ния
в СМУК-представление. Обычно эта работа выполняется средствами ОС, поскольку
формулы пересчета RGB СМУК просты.
Задание. ВьшеДите формулы связи межДу значениями цветовых компонент моделей RGB и СМУК.
![]() Цветовая модель HSB
Цветовая модель HSB
Цветовая модель HSB (Hue—Saturation—Brightness) описывает цветовое пространство через такие характеристики цвета, как цветовой оттенок, насыщенность и яркость.
Эти понятия были описаны в п. 2.4.3, дополним их более формальным определением.
Определение 11. Чистый цветовой тон —
один из цветов спектрального разложения света. Цветовой оттенок ![]() смесь чистого
цветового тона с серым цветом. Насыщенность цвета, или степень чистоты цвета —
доля чистого тона в цветовой смеси (чем больше серого, тем меньше
насыщенность). Яркость характеризуется общей светлостыо смешиваемых цветов (чем
больше черного, тем меньше яркость).
смесь чистого
цветового тона с серым цветом. Насыщенность цвета, или степень чистоты цвета —
доля чистого тона в цветовой смеси (чем больше серого, тем меньше
насыщенность). Яркость характеризуется общей светлостыо смешиваемых цветов (чем
больше черного, тем меньше яркость).
В модели HSB цвет описывается тройкой
чисел {цветовой оттенок, яркость, насыщенность}. Рассмотрим ряд ![]() цветов:
красный, темно-красный, красновато-черный, алый, розовый, бледно-розовый. В
модели HSB эти цвета -— производные от красного цвета и отличаются друг от
друга только яркостью и насыщенностью красного оттенка. Такое описание цвета (в
отличие от моделей RGB и СМУК) очень точно передает суббективное восприятие цвета
человеком, а не технические особенности воспроизведения цветов. Подобные
описания широко используются во всех областях искусства и производства, где
приходится иметь дело с цветом.
цветов:
красный, темно-красный, красновато-черный, алый, розовый, бледно-розовый. В
модели HSB эти цвета -— производные от красного цвета и отличаются друг от
друга только яркостью и насыщенностью красного оттенка. Такое описание цвета (в
отличие от моделей RGB и СМУК) очень точно передает суббективное восприятие цвета
человеком, а не технические особенности воспроизведения цветов. Подобные
описания широко используются во всех областях искусства и производства, где
приходится иметь дело с цветом.
![]() Таким образом, пространство HSB
организовано следующим образом (рис. 2.1):
Таким образом, пространство HSB
организовано следующим образом (рис. 2.1): ![]() ось конуса — это ось
яркости;
ось конуса — это ось
яркости; ![]() ось цветовых оттенков — окружность в
основании конуса;
ось цветовых оттенков — окружность в
основании конуса;
• насыщенность цвета определяется как угол между осью симметрии конуса и лучом, проходящим через вершину конуса и заданную точку.
Ось цветовых оттенков строится следующим образом: цвета спектра, от красного до фиолетового, и оттенки фиолетово-красного (которых нет в спектре) размещаются на окружности. Точку, соответствующую чистому красному цвету, принимают за ноль на круговой шкале цветовых оттенков (рис. 2.2). Все величины измеряют либо в градусах (0 0 —360 0 ), либо в условных единицах от О до 1. На оси конуса расположены оттен-
желтый зеленый
![]() оранжевый
оранжевый
голубой красный
пурпурный
Ось
черный
Рис. 2.1. Цветовое пространство модели HSB
ки серого цвета. Чем ближе к краю конуса, тем насыщеннее цвета.
Зеленый Желтый 600
![]() 1200
1200
Голубой- Красный
00
Рис. 2.2. Разрез конуса в плоскости постоянной яркости
Вопрос. Для чего к цветовым оттенкам на цветовой шкале были Добавлены оттенки фиолетово-красного цвета?
Ответ. Проходя сквозь призму или
дифракционную решетку, световые лучи с различными длинами волн отклоняются на
разные углы: призмы и дифракционные решетки осуществляют пространственное
разделение света. Если за призмой поставить белый экран, то преломленный в
призме луч белого света создаст на экране разноцветную полосу — спектр. Каждый
цвет спектра является монохромным (как излучение лазера) — он создается лучами
определенной длины волны. В спектре присутствуют цветовые оттенки от красного
до фиолетового, но нет промежуточных оттенков фиолетово-красного, так ![]() что
спектральные цвета нельзя «замкнуть» в непрерывную круговую ось. Однако в
природе такие цвета есть, например малиновый, пурпурный и т. д. (но они имеют
принципиально составной характер).
что
спектральные цвета нельзя «замкнуть» в непрерывную круговую ось. Однако в
природе такие цвета есть, например малиновый, пурпурный и т. д. (но они имеют
принципиально составной характер).
Все три рассмотренные цветовые модели (RGB, СМУК, HSB) описывают одно и то же реально существующее цветовое пространство. Их взаимный анализ позволяет отметить следующее:
![]() в цветовом пространстве модели HSB очень
хорошо видна связь между моделями RGB и СМУК: на цветовом круге основные цвета
одной модели расположены точно напротив основных цветов другой модели;
в цветовом пространстве модели HSB очень
хорошо видна связь между моделями RGB и СМУК: на цветовом круге основные цвета
одной модели расположены точно напротив основных цветов другой модели; ![]() кроме
того, если на цветовом круге отметить точками основные цвета RGB-MogxeJIYI, то
они образуют равносторонний треугольник, то же самое можно сказать и
относительно модели СМ УК;
кроме
того, если на цветовом круге отметить точками основные цвета RGB-MogxeJIYI, то
они образуют равносторонний треугольник, то же самое можно сказать и
относительно модели СМ УК; ![]() цвета модели HSB, которые не попадают в
этот треугольник, в
цвета модели HSB, которые не попадают в
этот треугольник, в ![]() будут непредставимы. То же самое можно
сказать и относительно модели СМУК.
будут непредставимы. То же самое можно
сказать и относительно модели СМУК.
Модель HSB позволяет представить (закодировать) практически все цвета, воспринимаемые человеком. Модели RGB и СМ УК описывают возможности компьютерных устройств по воспроизведению цвета. И оказывается, что некоторые цвета в принципе не могут быть воспроизведены на компьютере.
Вопрос. С какой целью основные цвета
RGB-M(Me.nu расположены на цветовой оси модели HSB так, что они образу![]() ют
равносторонний треугольник?
ют
равносторонний треугольник?
Ответ. Равносторонний треугольник имеет
наибольшую площадь среди всех треугольников, вписанных в задан![]() ную
окружность (докажите это), т. е. при таком выборе основных цветов количество
воспроизводимых цветов при переходе от модели HSB к модели RGB будет
максимальным.
ную
окружность (докажите это), т. е. при таком выборе основных цветов количество
воспроизводимых цветов при переходе от модели HSB к модели RGB будет
максимальным.
Вопросы и задания
1. ![]() Будем
считать, что каждый пиксель черно-белого изображения кодируется 1, если он
окрашен, и О — в противном случае. Декодируйте черно-белое изображение, оцифро
Будем
считать, что каждый пиксель черно-белого изображения кодируется 1, если он
окрашен, и О — в противном случае. Декодируйте черно-белое изображение, оцифро![]() ванное следующим образом (каждая строка изображения закодирована здесь
четырехзначным шестнадцатеричным числом):
ванное следующим образом (каждая строка изображения закодирована здесь
четырехзначным шестнадцатеричным числом):
а) 0070 OOFC OOF7 OOFF 8078 собо СОТО FFF8 FFB8
FF38 8Е78 EOFO 7FEO•,
6) 0100 0180 010 ОIЕО 01FO 01F8 01FC 01FE 0180 0180 7FFE 3FFC 1FF8 OFFO.
2. Рассчитайте объем видеопамяти, необходимой для хранения графического изображения, занимающего весь экран монитора с разрешением 640 х 480 и количеством отображаемых цветов, равным 65 536.
З. Подсчитайте объем информации, передаваемой от видеоадаптера к монитору в видеорежиме 1024 х 768 пикселей с глубиной цвета 24 бита и частотой обновления экрана 85 Гц.
4. Вы хотите
работать с разрешением 1600 х 1200 пикселей, используя 16 777 216 цветов. В
магазине продаются видеокарты с памятью 512 Кбайт, 2 Мбайта, 4 Мбайта и 64 ![]() Мбайта.
Какие из них можно купить для вашей работы?
Мбайта.
Какие из них можно купить для вашей работы?
5. Зачем нужны видеокарты с размером видеопамяти 128 Мб и более?
6.
|
Голубой (нет к асного) |
Желтый (нет синего) |
Пурпурный (нет зеленого) |
Цвет |
|
|
|
|
|
|
|
|
1 |
Пу пурный |
|
|
1 |
|
Желтый |
|
1 |
|
|
Голубой |
|
|
1 |
1 |
|
|
1 |
|
|
|
|
1 |
1 |
|
|
|
1 |
1 |
1 |
|
S 2.5. Представление звуковой информации
Звук — это волновые колебания давления в упругой среде (в воздухе, воде, металле и т. д.). Для обозначения звука часто используют термин «звуковая волна» .
![]()
Основные параметры любых волн, и звуковых в том числе, — частота и амплитуда колебаний. Частоту звука измеряют в герцах (Гц, количество колебаний в секунДУ). Человеческое ухо способно воспринимать звук в широком диапазоне частот, примерно от 16 Гц до 20 кГц. В нетехнических областях (например, в музыке) вместо термина «частота» нередко используют термин «тон» .
Амплитуду звуковых колебаний называют
звуковым Давлением или силой звука, эта величина характеризует воспринимаемую
громкость звука. Абсолютную величину звукового давления измеряют в единицах
давления ![]()
![]() паскалях (Па). Самые слабые, едва
различимые звуки имеют амплитуду около 20 мкПа (2•10-5 Па, так называемый порог
слышимости). Самые сильные звуки, еще не выводящие слуховые органы из строя,
могут иметь амплитуду до 200 Па (так называемый болевой порог). Из-за столь
широкого диапазона значений (максимальное и минимальное значения отличаются на
6—7 порядков!) абсолютными величинами звукового давления пользоваться крайне
неудобно, на практике обычно используют логарифмическую шкалу Децибелов.
паскалях (Па). Самые слабые, едва
различимые звуки имеют амплитуду около 20 мкПа (2•10-5 Па, так называемый порог
слышимости). Самые сильные звуки, еще не выводящие слуховые органы из строя,
могут иметь амплитуду до 200 Па (так называемый болевой порог). Из-за столь
широкого диапазона значений (максимальное и минимальное значения отличаются на
6—7 порядков!) абсолютными величинами звукового давления пользоваться крайне
неудобно, на практике обычно используют логарифмическую шкалу Децибелов.
Относительную силу звука, или уровень звука, определяют как логарифм отношения абсолютной величины звукового давления к величине порога слышимости, умноженныЙ на некоторый постоянный коэффициент. Уровень звука измеряют в особых единицах Децибелах (обозначаются ДБ). Ниже приводится формула расчета уровня звука:
![]()
Логарифмическая шкала децибелов на практике весьма удобна, хотя поначалу пользоваться ей непривычно:
![]() весь диапазон слышимых звуков составляет
0—140 дБ: О дБ — порог слышимости, 140 дБ — болевой порог;
весь диапазон слышимых звуков составляет
0—140 дБ: О дБ — порог слышимости, 140 дБ — болевой порог; ![]() человеческое
ухо способно уловить различие в громкости, если звуки отличаются по силе не
менее, чем на 1096 , что соответствует разнице в уровнях примерно на 1 дБ;
человеческое
ухо способно уловить различие в громкости, если звуки отличаются по силе не
менее, чем на 1096 , что соответствует разнице в уровнях примерно на 1 дБ; ![]() двукратное
различие в амплитуде звуков соответствует различию уровней в 6 дб;
двукратное
различие в амплитуде звуков соответствует различию уровней в 6 дб; ![]() если
уровни звуков отличаются на 20 дБ, то амплитуды отличаются в 10 раз, а разница
в 40 дБ СООТВ?гСТвует 100-кратному различию в амплитудах.
если
уровни звуков отличаются на 20 дБ, то амплитуды отличаются в 10 раз, а разница
в 40 дБ СООТВ?гСТвует 100-кратному различию в амплитудах.
Приведем некоторые значения уровней звука:
|
Порог слышимости |
|
|
Шо ох листьев, шум слабого ветра |
10-20 дБ |
|
Шепот (на задней парте) |
20-30 дБ |
|
Разговор средней громкости в кабинете ди ектора) |
50-60 дБ |
|
Автомагист аль с интенсивным движением |
80-90 дБ |
|
Авиадвигатели |
120-130 дБ |
|
Болевой порог |
-140 дБ |
2.5, 1 , Понятие звукозаписи
Звукозапись — это процесс сохранения информации о параметрах звуковых волн. Способы хранения, или записи, звука разделяются на аналоговые и цифровые. При аналоговой записи на носителе размещается непрерывный «слепок» звуковой волны. Так, на грампластинке пропечатывается непрерывная канавка, изгибы которой повторяют амплитуду и частоту звука, а на магнитной ленте параметры звука сохраняются в виде намагниченности рабочей поверхности, степень намагниченности непрерывно изменяется, повторяя параметры звука.
В компьютерах применяется исключительно цифровая форма записи звука. При цифровой записи звук необходимо подвергнуть временнбй Дискретизации и квантованию: параметры звукового сигнала измеряются не непрерывно, а через определенные промежутки времени (временная дискретизация); результаты измерений записываются в цифровом виде с ограниченной точностью (квантование).
Цифровая запись вносит двойное искажение в сохраняемые параметры сигнала: во-первых, при дискретизации теряется информация об истинном изменении звука между измерениями, а во-вторых, при квантовании со-
Исходный сигнал
•
![]() Сохраняемые
значения
Сохраняемые
значения
Теряемая информация : об истинном изменении во времени
• об истинных значениях амплитуды
храняются не точные параметры, а только близкие к ним дискретные значения.
В компьютерах используются так называемые импульсно-кодовое и частотное представления звуковой информации, для обозначения которых чаще всего используют названия технических способов воспроизведения звука: импульсно-њоДовая модуляция и частотная модуляция. Здесь мы рассмотрим первый из них.
2.5.2. Импульсно-кодовая модуляция
Импульсно-кодовая модуляция (англ. Pulse Code Modulation, РСМ) заключается в том, что звуковая информация хранится в виде значений амплитуды, взятых в определенные моменты времени (т. е. измерения проводятся «импульсами»).
При записи звука в компьютер амплитуда измеряется через равные интервалы времени с некоторой достаточно большой частотой.
Исходный сигнал Хранимая информация Воспроизводимый сигнал
Процесс получения цифровой формы звука называют оцифровкой. Устройство, выполняющее оцифровку звука, называется аналого-цифровым преобразователем (АЦП). Устройство, выполняющее обратное преобразование, из цифровой формы в аналоговую, называется цифро-аналоговым преобразователем (ЦАП). В современных компьютерах основная обработка звука выполняется звуковыми картами. Помимо АЦП и ЦАП звуковые карты содержат сигнальный процессор специализированный микрокомпьютер для обработки оцифрованного звука, выполняющий значительную часть рутинных расчетов при обработке звуков (смешение звуков, наложение спецэффектов,
расчет формы выходного сигнала и т. п.; центральный ![]() процессор
не тратит время на выполнение этих работ).
процессор
не тратит время на выполнение этих работ).
Определение 12. Моменты измерения амплитуды называют отсчетами. Частоту, с которой производят измерения сигнала, называют частотой Дискретизации.
Квантование звука заключается в следующем. Сначала мгновенные значения звукового давления измеряются с ограниченной точностью, затем, как и в случае с квантованием цветов, диапазон значений амплитуды разбивается на подуровни. По измеренному значению определяется подуровень, в который попадает значение, и в компьютере сохраняется только его номер. Количество бит, используемых для записи номеров подуровней, называется глубиной коДирования звука.
Если сравнить способы представления графической и звуковой информации, то импульсное кодирование звука соответствует растровому представлению изображений:
•
• время (в графике — пространство) априори разбивается на небольшие области; в пределах этих областей параметры звука (изображения) считахотся постоянными •
![]() При рассмотрении
представления графической информации упоминалось, что растровое представление
изображения не требует хранения координат отдельных пикселей. Аналогично, при
сохранении импульсного представления звука достаточно единожды сохранить
параметры оцифровки (глубину кодирования, частоту дискретизации и длительность
звукового фрагмента), а затем сохранять только номера подуровней единым
потоком.
При рассмотрении
представления графической информации упоминалось, что растровое представление
изображения не требует хранения координат отдельных пикселей. Аналогично, при
сохранении импульсного представления звука достаточно единожды сохранить
параметры оцифровки (глубину кодирования, частоту дискретизации и длительность
звукового фрагмента), а затем сохранять только номера подуровней единым
потоком.
Увеличивая частоту дискретизации и глубину кодирования, можно более точно сохранить и впоследствии восстановить форму звукового сигнала. При этом улучшается субъективное качество оцифрованного звука, однако увеличивается объем сохраняемых данных. При цифровой записи звука в различных случаях используют разные значения частоты дискретизации и глубины кодирования. Например, в цифровых автоответчиках используют частоту дискретизации 8—11 кГц и 8 бит для записи амплитуды, а стандарт записи звука на компакт-дисках соответствует частоте дискретизации 44,1 кГц и 16 бит для амплитуды на каждый аудио-канал (стереозвук — 2 канала, моно — один канал).
Пример 28. Оценим объем стереоаудиофайла в формате РСМ с глубиной кодирования 16 бит и частотой дискретизации 44,1 кГц, который хранит звуковой фрагмент длительностью звучания 1 секунда.
Объем такого звукового фрагмента равен:
16 бит х 44100 Гц х 2 (канала) 1 411 200 бит ![]() =
176 400 байт 172,3 Кбайт.
=
176 400 байт 172,3 Кбайт.
Возникает вполне естественный вопрос: до
какой степени можно уменьшать параметры оцифровки (а значит, ![]() и объем
оцифрованного звукового фрагмента), чтобы при восстановлении Звук оставался
достаточно близок к исходному?
и объем
оцифрованного звукового фрагмента), чтобы при восстановлении Звук оставался
достаточно близок к исходному?
![]() Котельников
Владимир Александрович (1908 г. р.), академик АН СССР, область научных
интересов радиотехника. Основные труды посвящены проблемам
совершенствования методов радиоприема, изучению помех радиоприему и разработке
методов борьбы с ними. В. А. Котельников
Котельников
Владимир Александрович (1908 г. р.), академик АН СССР, область научных
интересов радиотехника. Основные труды посвящены проблемам
совершенствования методов радиоприема, изучению помех радиоприему и разработке
методов борьбы с ними. В. А. Котельников
Теорема Найквиста—Котельникова—Шеннона утверждает, что если имеется сигнал U(t), спектр которого ограничен сверху частотой f, то после его дискретизации с частотой 1' > 2'f форму исходного сигнала можно точно восстановить по дискретным значениям (отсчетам), по следующей формуле:
![]() ЬТ(КМ)
ЬТ(КМ)![]()
27tF(t - КМ)
где = 1/F — время между
отсчетами, ![]() — время К-го отсчета,
— время К-го отсчета,
U(kM) значение К-го отсчета.
Покажем, почему частота дискретизации должна быть как минимум вдвое выше частоты сигнала. Допустим, на вход АЦП был подан синусоидальный сигнал, и АЦП выдал его цифровое представление. Вопрос: можно ли однозначно определить форму входного сигнала?
|
А (амплитуда) |
||||
|
|
|
|
||
|
|
|
|
||
Рис. 2.3
Вообще говоря, точная формулировка теоремы Найквиста—Котельникова применима только к сигналам -с неизменными частотными характеристиками и бесконечной длительностью, так что для оцифровки реальных звуковых сигналов частоту дискретизации выбирают с небольшим запасом.
Пример 29. Продемонстрируем использование теоремы Найквиста—Котельникова на практике.
2.5.3. Формат МТ
В 80-х годах прошлого века появились
электронные му![]() зыкальные инструменты — синтезаторы,
способные воспроизводить не только звуки многих существующих музыкальных
инструментов, но и абсолютно новые звуки.
зыкальные инструменты — синтезаторы,
способные воспроизводить не только звуки многих существующих музыкальных
инструментов, но и абсолютно новые звуки. ![]()
![]() Было разработано
соглашение о системе команд универсального синтезатора, получившее название
стандарта MIDI (англ. Musical Instrument Digital Interface). Запись
музыкального произведения в формате MIDI — последовательность закодированных
сообщений синтезатору. Сообщение может быть командой (нажать или отпустить
определенную клавишу, изменить высоту или тембр звучания), описанием параметров
воспроизведения (например, силы давления на клавиатуру) или управляющим
сообщением (включение полифонического режима, синхронизирующее сообщение).
Было разработано
соглашение о системе команд универсального синтезатора, получившее название
стандарта MIDI (англ. Musical Instrument Digital Interface). Запись
музыкального произведения в формате MIDI — последовательность закодированных
сообщений синтезатору. Сообщение может быть командой (нажать или отпустить
определенную клавишу, изменить высоту или тембр звучания), описанием параметров
воспроизведения (например, силы давления на клавиатуру) или управляющим
сообщением (включение полифонического режима, синхронизирующее сообщение).
![]() делают запись
музыкальной информа
делают запись
музыкальной информа![]() ции более компактной, чем импульсное
кодирование. Если сравнить способы представления графической и звуковой
информации, то запись звука в виде MIDIкоманд соответствует векторному
представлению изображений .
ции более компактной, чем импульсное
кодирование. Если сравнить способы представления графической и звуковой
информации, то запись звука в виде MIDIкоманд соответствует векторному
представлению изображений .
Записанные звуковые файлы можно редактировать,
т. е. вырезать, копировать и вставлять
фрагменты из других файлов. Кроме того, можно увеличивать или уменьшать
громкость, применять различные звуковые эффекты (эхо, уменьшение или увеличение
скорости воспроизведения, воспроизведение в обратном направлении и др.), а
также накладывать файлы друг на друга ![]() (микшировать).
(микшировать).
2.5.4. Принципы компьютерного воспроизведения звука
В современной цифровой звукотехнике (например, в компьютерных звуковых картах) используют несколько методов реконструкции формы аналогового сигнала. Эти методы сильно отличаются друг от друга даже идеями, взятыми за их основу.
Общим в методах реконструкции формы сигнала является то, что цифровой сигнал сперва подвергается переДискретизации — увеличению частоты дискретизации и глубины квантования в несколько раз (например, поток звуковых данных с Audio СГ) с частотой дискретизации 44,1 кГц и глубиной квантования 16 битов, в звуковой карте преобразуется в поток с частотой дискретизации 192 кГц и глубиной квантования 24 бита).
Для вычисления амплитуд сигнала во
вставленных новых отсчетах используются различные математические методы,
например полиномиальная интерполяция. Суть этого метода состоит в том, что по
известным значениям функции f(x) в дискретных моментах времент х ![]()
![]() х мы
можем восстановить ее значения в других точках х, т. е. по нескольким подряд
идущим отсчетам можно построить интерполяционный многочлен, проходящий через
заданные точки (например, интерполяционный многочлен Лагранжа). По «старым»
значениям отсчетов сигнала вычисляются коэффициенты многочлена, и с их помощью
вычисляется амплитуда сигнала в отсчетах, которые вставляются при
передискретизации (рис. 2.4).
х мы
можем восстановить ее значения в других точках х, т. е. по нескольким подряд
идущим отсчетам можно построить интерполяционный многочлен, проходящий через
заданные точки (например, интерполяционный многочлен Лагранжа). По «старым»
значениям отсчетов сигнала вычисляются коэффициенты многочлена, и с их помощью
вычисляется амплитуда сигнала в отсчетах, которые вставляются при
передискретизации (рис. 2.4).
![]() Интерполяция
Интерполяция
Исходные отсчеты
Добавленные отсчеты
После передискретизации цифровой сигнал с помощью ЦАП преобразуется в ступенчатый аналоговый сигнал. Этот ступенчатый сигнал представляет собой сумму ожидаемого выходного сигнала и так называемого паразитного сигнала дискретизации. Паразитный сигнал имеет малую амплитуду и очень высокую частоту. Выходной сигнал ЦАП пропускается через пропускающий фильтр низких частот, который подавляет высокочасТОТНЫе составляющие сигнала. Такой технический прием позволяет добиться качественной реконструкции формы аналогового сигнала при простой реализации электронных схем (см. рис. в Приложении).
Вопросы и задания
1. Каким образом происходит преобразование непрерывного звукового сигнала в дискретный цифровой код?
2. Перечислите достоинства и недостатки двух способов звукозаписи: импульсной модуляции и MIDI.
З. Можно ли записать с помощью синтезатора вокальные произведения?
4. Оцените информационный объем моноаудиофайла длительностью звучания 1 минута, если глубина квантования и частота дискретизации звукового сигнала равны соответственно 16 бит и 8 кГц.
5. Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен 700 Кбайт.
S 2.6. Методы сжатия цифровой информации
Характерной особенностью большинства «классических» типов информации, с которыми работают люди, является их избыточность.
Пример 31. Одним из примеров
проявления избыточности информации и ее сжатия является использование
математических обозначений. Например, сумма чисел 2, 4, 6, 8, 10, 12, 14, 16,
18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40 записывается так: ![]()
2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 + 22 + + 24 + 26 + 28 + 30 + 32 + 34 + 36 + 38 + 40.
Нетрудно заметить, что эта сумма составлена из всех четных чисел от 2 до 40. Используя математическую нотацию, эту сумму можно записать намного короче:
20
Е 2 • Г. Итак, введя новые обозначения, мы сумели со-
красить запись математического выражения, а значит, сжать информацию. Однако если первая форма записи понятна любому, кто учил азы математики, то вторая понятна только тем, кто знает, как следует интерпретировать эту запись.
Пример с суммой позволяет продемонстрировать
еще одну особенность методов сжатия степень сжатия входных данных принципиально
зависит от самих сжимаемых данных. Так, чтобы воспользоваться обозначением
суммы, надо найти формулу, выражающую складываемые числа через индекс
суммирования. И хотя ка![]() кую-нибуДь формулу можно вывести для любой
конечной последовательности (например, с помощью интерполяционной формулы
Лагранжа), но вот компактную формулу подобрать удается далеко не всегда! Пример
«плохой» последовательности:
кую-нибуДь формулу можно вывести для любой
конечной последовательности (например, с помощью интерполяционной формулы
Лагранжа), но вот компактную формулу подобрать удается далеко не всегда! Пример
«плохой» последовательности:
+ 123 + 129 + 131 + 137
+ 141 + 143 + 147, ![]()
Каждое число в данном ряду получено прибавлением 100 к простому числу. Увы, общая формула для всех простых чисел до сих пор не найдена, равно как не доказано существование или отсутствие такой формулы (проблема «генератора простых чисел»). Впрочем, для конечного числа простых чисел или для простых чисел с особой структурой формулы-генераторы существуют.
![]() Дадим формальное
определение избыточности информации.
Дадим формальное
определение избыточности информации.
Определение 13. Кодирование информации является избыточным, если количество бит в полученном коде больше, чем это необходимо для однозначного декодирования исходной информации.
Степень избыточности зависит от типа
информации: у видеоинформации она в несколько раз больше, чем у графической
информации, а степень избыточности последней в несколько раз больше, чем
текстовой информации. Вообще, степень избыточности естественной информации
достаточно велика. Клод Шеннон, исследовав избыточность литературного
английского языка, установил, что она составляет около 5096. Это означает, что
если в английском тексте наугад стереть около половины букв, то по оставшимся
буквам человек, знающий английский язык, почти наверняка сможет восстановить
текст. Избыточность языка выполняет очень важную функцию обеспечивает человеку
надежность ее восприятия, особенно в неблагоприятных условиях (просмотр
телепередач при наличии помех, чтение текстов в условиях недостаточной
освещенности, разговор в ваго![]() не метро и т. п.).
не метро и т. п.).
Хранение и передача информации требуют
определенной затраты ресурсов. Сжатие данных (перед сохранени![]() ем или
передачей по каналам связи) позволяет уменьшить эти затраты. На практике такие
затраты можно даже выразить в денежном эквиваленте: например, на скачивание из
Интернета сжатого музыкального файла потребуется меньше времени, а значит,
придется мень
ем или
передачей по каналам связи) позволяет уменьшить эти затраты. На практике такие
затраты можно даже выразить в денежном эквиваленте: например, на скачивание из
Интернета сжатого музыкального файла потребуется меньше времени, а значит,
придется мень![]() ше заплатить денег за пользование
Интернетом.
ше заплатить денег за пользование
Интернетом.
2.6.1 . Алгоритмы обратимых методов
Все методы сжатия можно поделить на два больших класса. Одни алгоритмы только изменяют способ представления входных данных, приводя их к форме, которая более компактно кодируется. Такие алгоритмы принято называть обратимыми, поскольку для них существуют обратные алгоритмы, которые могут точно восстановить исходные данные из сжатого массива. Другие алгоритмы выделяют во входных данных существенную информацию и ту часть, которой можно пренебречь и удалить, после чего оставшиеся «существенные» данные подвергаются дальнейщему сжатию. Такие алгоритмы принято называть алгоритмами с регулируемой потерей информации.
Определение 14. Метод сжатия называется обратимым, если из данных, полученных при сжатии, можно точно восстановить исходный массив данных.
Обратимые методы можно применять для сжатия любых типов данных. Характерными форматами файлов, хранящих сжатую без потерь информацию, являются:
![]() GIF, TIF, РСХ, PNG — для графических
данных;
GIF, TIF, РСХ, PNG — для графических
данных;
![]() AVI — для видеоданных;
AVI — для видеоданных;
, ар, ARJ, RAR, ИН, LH, САВ — для любых типов данных.
Существует достаточно много обратимых методов сжатия данных, однако в их основе лежит сравнительно небольшое количество теоретических алгоритмов, которые мы рассмотрим более подробно.
Метод упаковки
Суть метода упаковки заключается в уменьшении количества бит, отводимых для кодирования символов, если в сжимаемом массиве данных присутствует только небольшая часть используемого алфавита.
вола входного текста одним байтом в
выходном массиве. В результате получим двукратное сжатие данных. Формат записи
чисел, при котором число записывается в десятичной системе, а цифры числа
кодируются 4-битовыми кодами, называется ВСГ)-форматом (Binary Coded Decimal,
или двоично-десятичная запись). ВСГ)-формат ![]() нередко используется
в программировании для хране
нередко используется
в программировании для хране![]() ния целых чисел, например в базах данных.
ния целых чисел, например в базах данных.
Пример 33. Входной текст «КОЛ ОКОЛО_КОЛОКОЛА» содержит всего 5 различных символов («К», «О», «Л», «А» и пробел), следовательно, каждый символ может быть закодирован тремя битами. Всего в исходном тек-
сте 18 символов, так что потребуется 18 • З = 54 бита. Округлив это значение с избытком до целого числа байт, получим размер сжатого массива — всего 7 байт. Коэффициент сжатия равен 18/7 = 2,(571428) 2,6.
Байты выходных данных Нумерация битов в байтах
Одно из преимуществ метода упаковки
заключается в том, что любой фрагмент сжатых данных можно распа![]() ковать,
совершенно не используя предшествующие данные. Действительно, зная номер
требуемого символа и длину кодов символов М, можно вычислить местоположение
кода символа в сжатом массиве данных:
ковать,
совершенно не используя предшествующие данные. Действительно, зная номер
требуемого символа и длину кодов символов М, можно вычислить местоположение
кода символа в сжатом массиве данных:
![]() номер
байта, в котором начинается код символа, вы
номер
байта, в котором начинается код символа, вы![]() числяется так: L =
[M•N/8];
числяется так: L =
[M•N/8];
![]()
Метод упаковки дает хорошие результаты, только если множество используемых символов невелико. Например, если в тексте используются только прописные русские буквы и знаки препинания, то текст может быть сжат всего на 25 0/0 : 33 русские буквы плюс пробел и знаки препинания — итого около 40 символов. Для их кодирования достаточно 6 бит. При упаковке текст уменьшится до от первоначального объема.
Алгоритм Хаффмана
Слабое место метода упаковки заключается в том, что символы кодируются битовыми последовательностями одинаковой длины. Например, любой текст, состоящий только из двух букв «А» и «В», сжимается методом упаковки в восемь раз. Однако если к такому тексту добавить всего лишь одну букву, например «С», то степень сжатия сразу уменьшится вдвое, причем независимо от длины текста и количества добавленных символов «С»!
Улучшения степени сжатия можно достичь, кодируя часто встречающиеся символы короткими кодами, а редко встречающиеся — более длинными. Именно такова идея метода, опубликованного Д. Хаффманом (Huffman) в 1952 г.
Идея кодирования символов кодами переменной длины была высказана и теоретически проработана американскими учеными К. Шенноном и Р. М. Фано. Ими был предложен алгоритм построения эффективных сжимающих кодов переменной длины (алгоритм Шеннона—Фано), однако он в некоторых случаях строил неоптимальные коды. Алгоритм Хаффмана оказался простым, быстрым и оптимальным: среди алгоритмов, кодирующих каждый символ по отдельности и целым количеством бит, он обеспечивает наилучшее сжатие.
![]() Дэвид Хаффман руководил кафедрой
компьютерных наук Массачусетского технологического института (Massachusetts
Institute of Technology — MIT). Хотя Хаффман больше известен как разработчик
метода построения минимально-избыточных кодов, он внес важный вклад во
множество областей, связанных с информатикой, в частД. Хаффман ности в
электронику.
Дэвид Хаффман руководил кафедрой
компьютерных наук Массачусетского технологического института (Massachusetts
Institute of Technology — MIT). Хотя Хаффман больше известен как разработчик
метода построения минимально-избыточных кодов, он внес важный вклад во
множество областей, связанных с информатикой, в частД. Хаффман ности в
электронику.
(1925-1999)
Алгоритм Хаффмана сжимает данные за два прохода: на первом проходе читаются все входные данные и подсчитываются частоты встречаемости всех символов. Затем по этим данным строится Дерево њоДирования Хаффмана, а по нему — коды символов. После этого, на втором проходе, входные данные читаются еще раз и при этом генерируется выходной массив данных.
Вычисление частот встречаемости
тривиальная задача. Разберем построение дерева кодирования ![]() Хаффмана.
Хаффмана.
Алгоритм построения дерева Хаффмана
1. Символы входного алфавита образуют список свободных узлов. Каждый узел имеет вес, равный количеству вхождений символа в исходное сообщение.
2. В списке выбираются два свободных узла с наименьшими весами.
З. Создается их узел- «родитель» с весом, равным сумме их весов, он соединяется с «детьми» дугами.
4. Одной дуге, выходящей из «родителя», ставится в соответствие бит 1, другой бит О.
5. «Родитель» добавляется в список свободных узлов, а двое его «детей» удаляются из этого списка.
6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.
Пример 34. Построение дерева Хаффмана и префиксных кодов для текста «КОЛ_ОКОЛО КОЛОКОЛА»:
Теперь для определения кода каждой конкретной буквы необходимо просто пройти от вершины дерева до этой буквы, выписывая нули и единицы по маршруту следования. В нашем примере символы получат следующие коды:
|
о |
00 |
|
|
01 |
|
л |
10 |
|
п обел |
110 |
|
|
111 |
После того как коды символов построены, остается сгенерировать сжатый массив данных, для чего надо снова прочесть входные данные и каждый символ заменить на соответствующий код.
В нашем случае непосредственно код текста будет занимать 39 бит, или 5 байт. Коэффициент сжатия равен 18/5 = 3,6.
Код Хаффмана является префиксным. Это означает, что код каждого символа не является началом кода какого-либо другого символа. Код Хаффмана однозначно восстановим, даже если не сообщается длина кода каждого переданного символа. Подробнее об этом вы узнаете в главе 5. Получателю пересылают только дерево Хаффмана в компактном виде, а затем входная последовательность кодов символов декодируется им самостоятельно без какой-либо дополнительной информации.
Алгоритм RLE
В основу алгоритмов RLE (англ. Run-Length Encoding — кодирование путем учета числа повторений) положен принцип выявления повторяющихся последовательностей данных и замены их простой структурой: повторя-
Общая схема алгоритма LZ77 такова (это
не точное описание алгоритма): ![]()
![]() входные данные читаются последовательно, текущая позиция условно
разбивает массив входных данных на прочитанную и непрочитанную части;
входные данные читаются последовательно, текущая позиция условно
разбивает массив входных данных на прочитанную и непрочитанную части; ![]() для
цепочки первых байтов непрочитанной части ищется наиболее длинное совпадение в
прочитанной части. Если совпадение найдено, то составляется комбинация
{смещение, длина}, где смещение указывает, на сколько байтов надо сместиться
назад от текущей
для
цепочки первых байтов непрочитанной части ищется наиболее длинное совпадение в
прочитанной части. Если совпадение найдено, то составляется комбинация
{смещение, длина}, где смещение указывает, на сколько байтов надо сместиться
назад от текущей ![]() позиции, чтобы найти совпадение, а длина
— это длина совпадения;
позиции, чтобы найти совпадение, а длина
— это длина совпадения; ![]() если запись комбинации {смещение, длина}
короче совпадения, то она записывается в выходной массив, а текущая позиция перемещается
вперед (на длину совпадающей части);
если запись комбинации {смещение, длина}
короче совпадения, то она записывается в выходной массив, а текущая позиция перемещается
вперед (на длину совпадающей части); ![]() если совпадение не обнаружено или оно
короче записи комбинации {смещение, длина}, то в выходной массив копируется
текущий байт, текущая позиция перемещается вперед на 1, и анализ повторяется.
если совпадение не обнаружено или оно
короче записи комбинации {смещение, длина}, то в выходной массив копируется
текущий байт, текущая позиция перемещается вперед на 1, и анализ повторяется.
Общая схема алгоритма LZ78 такова (это
не точное ![]() описание алгоритма):
описание алгоритма):
![]() алгоритм во время сжатия текста создает специальный словарь
повторяющихся цепочек, в словаре каждой цепочке соответствует короткий код;
алгоритм во время сжатия текста создает специальный словарь
повторяющихся цепочек, в словаре каждой цепочке соответствует короткий код; ![]() для
цепочки первых байтов непрочитанной части ищется наиболее длинное совпадение в
словаре. Код совпадения записывается в выходной массив, туда же заносится
первый несовпавший символ, и текущая позиция перемещается вперед на длину
совпадения + 1;
для
цепочки первых байтов непрочитанной части ищется наиболее длинное совпадение в
словаре. Код совпадения записывается в выходной массив, туда же заносится
первый несовпавший символ, и текущая позиция перемещается вперед на длину
совпадения + 1; ![]() в словарь добавляется новое слово:
«совпадение» + + «несовпавший символ», и процесс повторяется до тех пор, пока
не будет сжат весь входной массив.
в словарь добавляется новое слово:
«совпадение» + + «несовпавший символ», и процесс повторяется до тех пор, пока
не будет сжат весь входной массив.
Алгоритмы Лемпеля—Зива тем лучше сжимают текст, чем больше размер входного массива. Характерной особенностью обратных алгоритмов LZ77 и LZ78 является то, что, кроме самих сжатых данных, никакой дополнительной информации им не требуется! Начав работать, эти алгоритмы по уже распакованной части восстанавливают информацию, необходимую для распаковки следующих частей сжатых данных. Для сравнения: в алгоритме Хаффмана вместе со сжатыми данными требуется сохранять дерево Хаффмана, иначе распаковка будет невозможна.
2.6.2. Методы сжатия с регулируемой потерей информации
Описанные выше алгоритмы являются обратимыми: любой массив входных данных при распаковке восстанавливается абсолютно точно. Поэтому обратимые алгоритмы можно применять для сжатия информации любого рода. Но, как оказалось, для аудио- и видеоинформации абсолютно точное восстановление вовсе необязательно. Проведенные в конце ХХ века исследования психофизиологических характеристик зрения и слуха обнаружили ряд особенностей человеческого восприятия, использование которых позволяет существенно увеличивать степень сжатия звуковой, графической и видеоинформации.
Например, было установлено, что глаз человека наиболее чувствителен к зеленому цвету, чувствительность к красному ниже примерно в 4 раза, а к синему — почти в 10 раз! А это означает, что на хранение информации о красной и синей составляющих цвета можно было бы отводить меньше бит. Но в большинстве форматов графических файлов это не так — цветовые компоненты кодируются одинаковым количеством бит. Этот пример показывает, что традиционные способы представления видеоинформации обладают очень большой степенью избыточности, при условии, что речь идет о воспроизведении видеоинформации для человека.
Для разработки и стандартизации эффективных методов сжатия аудио- и видеоинформации на рубеже 1980—1990-х годов были созданы Группа экспертов по фотографическим изображениям (Joint Photographic Experts Group, сокр. JPEG) и Группа экспертов по видеоизображениям (Motion Picture Experts Group, сокр. MPEG).
Наиболее известными методами сжатия с регулируемой потерей информации являются:
• JPEG — метод сжатия графических данных;
• MPEG — группа методов сжатия видеоданных;
• МРЗ — метод сжатия звуковых данных.
Эти методы непросты в реализации, в них используется достаточно сложный математический аппарат, выходящий за рамки школьной программы, поэтому далее будет приведено лишь обзорное описание методов.
Алгоритм JPEG
Алгоритм JPEG используется для сжатия статических изображений. Помимо сжимаемого изображения, алгоритму передается также желаемый коэффициент сжатия — этот параметр регулирует долю информации, которая будет удалена при сжатии.
Алгоритм JPEG способен упаковывать графические изображения в несколько десятков раз, при этом потери качества становятся заметными только при очень высоких коэффициентах сжатия.
Алгоритм МРЗ
Алгоритм МРЗ (точное название MPEG-1 Layer З) является частью стандарта MPEG и описывает сжатие аудиоинформации. Помимо сжимаемого звукового фрагмента алгоритму передается также желаемый битрейт (англ. bitrate) — количество бит, используемых для кодирования одной секунды звука. Этот параметр регулирует долю информации, которая будет удалена при сжатии.
Сжатие МРЗ также осуществляется в
несколько этапов: звуковой фрагмент разбивается на небольшие участки — фреймы
(англ. frames), а в каждом фрейме звук разлагается на составляющие звуковые
колебания, которые в физике называют гармониками. С точки зрения математики,
звук разлагается на группу синусоидальных колебаний с разными частотами и
амплитудами. Затем начинается психоакустическая обработка ![]() удаление
маловажной для человеческого восприятия звуковой информации, при этом
учитываются различные особенности слуха. Желаемый битрейт определяет, какие
эффекты будут учитываться при сжатии, а также количество удаляемой информации.
На последнем этапе оставшиеся данные сжимаются алгоритмом Хаффмана.
удаление
маловажной для человеческого восприятия звуковой информации, при этом
учитываются различные особенности слуха. Желаемый битрейт определяет, какие
эффекты будут учитываться при сжатии, а также количество удаляемой информации.
На последнем этапе оставшиеся данные сжимаются алгоритмом Хаффмана.
Алгоритм МРЗ позволяет сжимать звуковые файлы в несколько раз. При этом даже самый большой битрейт 320 Кбит/с стандарта МРЗ обеспечивает четырехкратное сжатие аудиоинформации по сравнению с форматом Audio СГ), при таком же субъективном качестве звука. Формат МРЗ стал стандартом де-факто для распространения музыкальных файлов через Интернет.
Алгоритмы MPEG
Одна из основных идей сжатия видео — метод «опорного кадра» — заключается в том, чтобы сохранять не целиком кадры, а только изменения кадров. Например, в фильме есть сцена беседы героев в комнате. При этом от кадра к кадру меняются только выражения лиц, а большая часть изображения неподвижна. Закодировав первый кадр сцены и отличия остальных ее кадров от первого, можно получить очень большую степень сжатия.
Еще один способ уменьшения кодируемой информации заключается в том, чтобы быстро сменяемые участки изображения кодировать с качеством, которое намного ниже качества статичных участков, — человеческий глаз не успевает рассмотреть их детально.
Кроме того, формат MPEG позволяет сохранять в одном файле несколько так называемых потоков данных. Так, в основном потоке можно сохранить фильм, в другом — логотип, в третьем — субтитры, и т. д. Потоки данных накладываются друг на друга только при воспроизведении. Такой способ позволяет, например, хранить субтитры в виде текста вместо изображений букв, логотип сохранить всего один раз, а не в каждом кадре, и т. п.
Разновидности формата MPEG отличаются друг от друга по возможностям, качеству воспроизводимого изображения и максимальной степени сжатия:
![]() MPEG-1 —
использовался в первых Video CD (VCD-I);
MPEG-1 —
использовался в первых Video CD (VCD-I); ![]() MPEG-2 используется
в DVD и Super Video CD (SVCD, VCD-II);
MPEG-2 используется
в DVD и Super Video CD (SVCD, VCD-II);
![]() MJPEG — формат
сжатия видео, в котором каждый кадр сжимается по методу JPEG;
MJPEG — формат
сжатия видео, в котором каждый кадр сжимается по методу JPEG;
![]() MPEG-4
— популярный эффективный формат сжатия видео;
MPEG-4
— популярный эффективный формат сжатия видео;
![]() DivX,
XviD — улучшенные модификации формата MPEG-4.
DivX,
XviD — улучшенные модификации формата MPEG-4.
Вопросы и задания
1. Для метода упаковки подсчитайте коэффициент сжатия текста, содержащего только прописные английские буквы, пробелы и знаки препинания (точка, запятая, дефис).
2.
З. Приведите примеры алгоритмов сжатия с потерей и без потери информации.
4. Что произойдет, если в упакованном методом RLE сообщении пропустить один байт?
5. Какова длина последовательности, после кодирования которой методом RLE получилось следующее:
![]()
6. Как надо поступить при ТЕ-кодировании, если количество идущих подряд одинаковых байтов больше 127 и не помещается в 7 разрядов?
7. Постройте дерево Хаффмана и выпишите коды символов для сообщения
![]()
Заключение
В этой главе мы подробно рассмотрели способы компьютерного представления числовой информации, которая была первым и долгое время оставалась единственным видом информации, обрабатываемой на компьютере. Вы узнали о способах представления целых и вещественных чисел, познакомились с понятием дополнительного кода и, надеемся, сможете объяснить, почему целые отрицательные числа представляются в такой «искусственной» форме.
На страницах этой главы мы познакомили
вас с достоинствами и недостатками форматов с плавающей и ![]() с
фиксированной запятой, а также с особенностями реализации целочисленной и
вещественной арифметик в ограниченном числе разрядов.
с
фиксированной запятой, а также с особенностями реализации целочисленной и
вещественной арифметик в ограниченном числе разрядов.
Мы постарались показать вам, насколько информатика связана с другими науками: физикой, биологией, колориметрией и, конечно, математикой.
Компьютер называют универсальной
машиной для обработки информации, при этом подчеркивают универсальность
двоичного кодирования информации. Но давайте задумаемся, всякую ли информацию
человек научился представлять в двоичном коде и всякую ли информацию может
обрабатывать компьютер? Что вы ![]() можете сказать, например, об осязательной
информации? Как сохранить в двоичном коде всевозможные запахи? Этот пример
говорит о том, что мы находимся еще в самом начале эры цифровых технологий.
можете сказать, например, об осязательной
информации? Как сохранить в двоичном коде всевозможные запахи? Этот пример
говорит о том, что мы находимся еще в самом начале эры цифровых технологий.
Глава З
![]()
Введение в алгебру логики ![]()
![]()
Я, по крайней мере, думал, что противоречить друг другу могут только высказывания, поскольку они через умозаключения ведут к новым высказываниям, и мне кажется, что мнение, будто сами факты и события могут оказаться в противоречии друг с другом, является классическим примером бессмыслицы.
Д. Гильберт
S 3.1. Алгебра логики. Понятие высказывания
S 3.2. Логические операции. Таблицы истинности
S 3.3. Логические формулы. Законы алгебры логики
S 3.4. Методы решения логических задач
S 3.5. Алгебра переключательных схем S 3.6. Булевы функции
S 3.7. Канонические формы логических формул.
Теорема о СДНФ
S 3.8. Минимизация булевых функций в классе дизъюнктивных нормальных форм
S 3.9. Полные системы булевых функций
S 3.10. Элементы схемотехники. Логические схемы
![]()
л гебра логики является частью, разделом
бурно развивающейся сегодня науки Дискретной математики. Дискретная математика
занимается изучением свойств структур конечного характера, кото![]() рые возникают
как внутри математики, так и в ее приложениях. Заметим, что классическая
математика, в основном, занимается изучением свойств объектов непрерывного
характера, хотя само деление математики на классическую и дискретную в
значительной мере условно, поскольку между ними происходит активная циркуляция
идей и методов, часто возникает необходимость исследовать модели, обладающие
как дискретными, так и непрерывными свойствами. К числу структур, изучаемых
дискретной математикой, могут быть отнесены конечные группы, конечные графы,
математические модели преобразователей информации типа конечных автоматов или
машин Тьюринга и др.
рые возникают
как внутри математики, так и в ее приложениях. Заметим, что классическая
математика, в основном, занимается изучением свойств объектов непрерывного
характера, хотя само деление математики на классическую и дискретную в
значительной мере условно, поскольку между ними происходит активная циркуляция
идей и методов, часто возникает необходимость исследовать модели, обладающие
как дискретными, так и непрерывными свойствами. К числу структур, изучаемых
дискретной математикой, могут быть отнесены конечные группы, конечные графы,
математические модели преобразователей информации типа конечных автоматов или
машин Тьюринга и др.
Математический аппарат алгебры логики широко используется в информатике, в частности, в таких ее разделах, как проектирование ЭВМ, теория автоматов, теория алгоритмов, теория информации, целочисленное программирование и т. д.
S 3.1 . Алгебра логики. Понятие высказывания
Алгебра логики изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например, {O, 1}). Иногда вместо термина «алгебра логики» употребляют термин «двузначная логика» .
![]() Отцом алгебры логики
по праву считается английский математик XIX столетия Джордж Буль. Именно он
построил один из разделов формальной логики в виде некоторой «алгебры»,
аналогичной алгебре чисел, но не сводящейся к ней. Алгебра в широком смысле
этого слова — наука об общих операциях, аналогичных сложению и умножению,
которые могут выполняться не только Дж. Буль над числами, но и над другими
математиче(1815-1864) сними объектами. Существуют алгебры натуральных чисел,
многочленов, векторов, матриц, множеств и т. д.
Отцом алгебры логики
по праву считается английский математик XIX столетия Джордж Буль. Именно он
построил один из разделов формальной логики в виде некоторой «алгебры»,
аналогичной алгебре чисел, но не сводящейся к ней. Алгебра в широком смысле
этого слова — наука об общих операциях, аналогичных сложению и умножению,
которые могут выполняться не только Дж. Буль над числами, но и над другими
математиче(1815-1864) сними объектами. Существуют алгебры натуральных чисел,
многочленов, векторов, матриц, множеств и т. д.
логики
![]()
Большой вклад в становление и развитие алгебры логики внесли Августус де Морган (1806—1871), Уильям Стенли Джевонс (1835—1882), Платон Сергеевич Порецкий (1846—1907), Чарлз Сандерс Пирс (1839—1914), Андрей Андреевич Марков (1903—1979), Андрей Николаевич Колмогоров (1903—1987) и др.
Долгое время алгебра логики была известна достаточно узкому классу специалистов. Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 году выдающийся американский математик и инженер Клод Шеннон (1916—2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования релейно-контактных и электронно-ламповых схем.
Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). С помощью высказываний мы устанавливаем своиства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Примерами высказываний на естественном языке являются предложения «Сегодня светит солнце» или «Трава растет». Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в нашем примере погоды и окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь» .
Однако определение истинности
высказывания далеко не простой вопрос. Например, высказывание «Число 1 + 2 2
= 4294 967 297 — простое», принадлежащее Ферма (1601—1665), долгое время
считалось истинным, пока в 1732 году Эйлер (1707—1783) не доказал, что оно
ложно. В целом, обоснование истинности или ложности простых высказываний
решается вне алгебры логики. Например, истинность или ложность высказывания
«Сумма углов треугольника равна 180 0 » устанавливает![]() ся
геометрией, причем в геометрии Евклида это высказывание является истинным, а в
геометрии Лобачевского ложным.
ся
геометрией, причем в геометрии Евклида это высказывание является истинным, а в
геометрии Лобачевского ложным.
![]()
Что же является высказыванием в формальной
логике? Определение 1. Высказывание — это языковое образование, в отношении
которого имеет смысл говорить о его истин![]() ности или ложности
(Аристотель),
ности или ложности
(Аристотель),
![]()
Это словесное определение, не являющееся математически точным, только на первый взгляд кажется удовлетворительным. Оно отсылает проблему определения высказывания к проблеме определения истинности или ложности данного языкового образования. Если рассматривать в качестве высказываний любые утвердительные предложения, то это быстро приводит к парадоксам и противоречиям. Например, предложению «Это предложение является ложным» невозможно приписать никакого значения истинности без того, чтобы не получить противоречие. Действительно, если принять, что предложение истинно, то это противоречит его смысЛУ. Если же принять, что предложение ложно, то отсюда следует, что предложение на самом деле истинно. Как видно, этому предложению осмысленно нельзя приписать какое-либо значение истинности, следовательно, оно не является высказыванием.
![]() Причина этого
парадокса лежит в структуре построения указанного предложения: оно ссылается на
свое собственное значение. С помощью определенных ограничений на допустимые
формы высказываний могут быть устранены такие ссылки на себя и, следовательно,
устранены возникающие отсюда парадоксы.
Причина этого
парадокса лежит в структуре построения указанного предложения: оно ссылается на
свое собственное значение. С помощью определенных ограничений на допустимые
формы высказываний могут быть устранены такие ссылки на себя и, следовательно,
устранены возникающие отсюда парадоксы.
Определение 2. Высказывание называется
простым (элементарным), если никакая его часть не является выска![]() зыванием.
зыванием.
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывание, соединив их знаком равенства или неравенства. Сами числовые выражения высказываниями не являются. Не являются высказываниями и равенства или неравенства, содержащие переменные. Например, предложение «х < 12» становится высказыванием при замене переменной каким-либо конкретным значением. Предложения типа «х < 12» называют преДикатами.
Алгебра логики отвлекается от смысловой содержательности высказываний. Мы можем договориться, что абсурдное по смыслу высказывание «Крокодилы летают» является истинным, и с этим значением высказывания будем работать. Вопрос о том, летают крокодилы
логики
![]()
или нет, может волновать зоологов, но никак не математиков:
им этот потрясающий факт безразличен. Введение таких ограничений дает
возможность изучать высказывания алгебраическими методами, позволяет ввести
операции над элементарными высказываниями и с их помощью строить и изучать
составные высказывания. В информатике для точного определения понятия
высказывания строятся ограниченные системы форм высказываний (формальный язык),
которые используются при описании алгоритмических языков, в информационных
системах, для строгого формального описания алгоритмов и т. д. ![]()
![]() Алгебра логики изучает строение (форму, структуру) сложных
логических высказываний и способы установления их истинности с помощью
алгебраических
Алгебра логики изучает строение (форму, структуру) сложных
логических высказываний и способы установления их истинности с помощью
алгебраических
методов.
Вопросы и задания
1. ![]() Из
данных предложений выберите те, которые являются высказываниями, и обоснуйте
свой выбор.
Из
данных предложений выберите те, которые являются высказываниями, и обоснуйте
свой выбор.
а) Коля спросил: «Который час?»
б) Как пройти в библиотеку?
в) Картины Пикассо слишком абстрактны.
г) Решение задачи — информационный процесс.
д) Число 2 является делителем числа 7 в некоторой системе счисления.
2. Объясните, почему формулировка любой теоремы является высказыванием.
З. Приведите по два примера истинных и ложных высказываний из биологии, географии, информатики, истории, математики, литературы.
4. Из данных высказываний выберите истинные.
а) Город Джакарта — столица Индонезии.
б) Решение задачи — информационный процесс.
в) Число 2 является делителем числа 7 в некоторой системе счисления.
г) Меню в программе — это список возможных вариантов.
д) Для всех х из области определения выражения х + 1 верно, что х + 2 > О.
![]()
е) Сканер — это устройство, которое
может напечатать на бумаге то, что изображено на экране компьютера.![]()
ж) П + > VIII.
з) Мышь — устройство ввода информации.
5. В приведенных предложениях вместо многоточий поставьте подходящие по смыслу слова «необходимо», «достаточно», «необходимо и достаточно» . Помните, что получившиеся высказывания должны быть истинными.
1) Для того чтобы число делилось на 4, чтобы оно было четным.
2) Чтобы число делилось на З, ... чтобы оно делилось на 9.
З) Для того чтобы число делилось на 10, . чтобы оно оканчивалось нулем.
4)
Чтобы произведение двух чисел равнялось нулю, ![]() чтобы
каждое из них равнялось нулю.
чтобы
каждое из них равнялось нулю.
5)
Чтобы произведение двух чисел равнялось нулю, ![]() чтобы хоть
одно из них равнялось нулю.
чтобы хоть
одно из них равнялось нулю.
6) Чтобы умножить сумму нескольких чисел на какое-нибудь число каждое слагаемое умножить на это число и произведения сложить.
7) Чтобы произведение нескольких чисел разделить на какое-нибудь число, ... разделить на это число только один из сомножителей и полученное частное умножить на остальные сомножители.
8) Для того чтобы сумма двух чисел была четным числом, ... чтобы каждое из слагаемых было четным числом.
9) Для того чтобы число делилось на 10, . . чтобы оно делилось на 5.
10) Для того чтобы число делилось на 6, . . чтобы оно делилось на 2 и на З.
11) Для того чтобы число делилось на 12, . . чтобы оно делилось на 2 и на З.
12) Чтобы четырехугольник был квадратом, ... чтобы все его стороны были равны.
S 3.2. Логические операции. Таблицы истинности
Употребляемые в обычной речи связки «и», «или», «не», «если то ...», «тогда и только тогда, когда ... » и т. п. позволяют из уже заданных высказываний строить новые сложные высказывания. Истинность или
ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как логических операций над высказываниями. Для обозначения истинности, как правило, используются символы «И» и «1», а для обозначения ложности — символы «Л» и «О».
![]() Логическая операция полностью может быть описана таблицей
истинности, указывающей, какие значения принимает сложное высказывание при всех
возможных значениях простых высказываний.
Логическая операция полностью может быть описана таблицей
истинности, указывающей, какие значения принимает сложное высказывание при всех
возможных значениях простых высказываний.
![]()
|
Логическая связка |
Названия логической опе а ии |
Обозначения |
|
не |
Отрицание, инверсия |
|
|
и, а, но, хотя |
Конъюнкция, логическое множение |
|
|
или |
Дизъюнкция, нестрогая дизъюнкция, логическое сложение |
|
|
либо если ..., то |
Разделительная (строгая) дизъюнкция, исключающее ИЛИ сложение по мо лю 2 Импликация, следование |
|
|
тогда и только тогда ког а |
Эквивалентность, эквивален ия, авнозначность |
|
Введем перечисленные логические операции формальным образом .
3.2.1. Высказывание, составленное из двух высказываний
путем объединения их связкой «и», называется конъюнкцией или логичиким
умножением. Высказывая конъюнкцию, мы утверждаем, что выполняются оба со![]() бытия,
о КОТОРЫХ идет речь в составляющих высказыва
бытия,
о КОТОРЫХ идет речь в составляющих высказыва![]() ниях. Например,
сообщая:
ниях. Например,
сообщая:
{Ивановы привезли на зиму уголь и закупили дрова на растопку камина}, мы выражаем в одном высказывании свое убеждение в том, что произошли оба этих события.
![]()
1
Это тем более необходимо, потому что связки, употребляемые в речи, неоднозначны.
Определение З. Конъюнкция — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны . Логическая операция конъюнкция определяется следующей таблицей, которую называют таблицей
истинности:
|
Р |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
1 |
1 |
![]() В русском языке конъюнкции соответствует не только союз
«и», но и другие речевые обороты, например связки «а» или «но» .
В русском языке конъюнкции соответствует не только союз
«и», но и другие речевые обороты, например связки «а» или «но» .
3.22. Высказывание, состоящее из двух высказываний, объединенных связкой «или», называется Дизъюнкцией или логическим сложением, нестрогой Дизъюнкцией. В высказываниях, содержащих связку «или», указывается на существование двух возможных событий, из которых хотя бы одно должно быть осуществлено. Например, сообщая:
{Петя читает книгу или пьет чай}, мы имеем в виду, что хотя бы что-либо одно Петя делает. При этом Петя может одновременно читать книгу и пить чай. И в этом случае дизъюнкция будет истинна.
![]()
1 Это определение легко распространяется на случай п высказываний (п > 2, п — натуральное число).
Определение 4. ДИЗЪЮНКЦИЯ — логическая операция, которая каждым двум элементарным высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны . Логическая операция дизъюнкция определяется следующей таблицей истинности:
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
1 |
|
1 |
|
1 |
1 |
1 |
Дизъюнкция истинна, когда хотя бы одно из двух образующих ее высказываний истинно.
Союз «или» может применяться в речи и в другом, «исключающем» смысле. Тогда он соответствует другому высказыванию — разделительной, или строгой дизъюнкции.
3.2.3. Высказывание, образованное из
двух высказываний, объединенных связкой «либо» (точнее: «либо только . ![]() либо
только ...»), называется разделительной (строгой) Дизъюнкцией, исключающим ИЛИ,
сложением по модулю 2.
либо
только ...»), называется разделительной (строгой) Дизъюнкцией, исключающим ИЛИ,
сложением по модулю 2.
В отличие от обычной дизъюнкции (связка «или»), в высказывании, являющемся разделительной дизъюнкцией, мы утверждаем, что произойдет только одно событие из двух. Например, сообщая:
{Петя сиДит нс трибуне А либо на трибуне Щ, мы утверждаем, что Петя сидит либо только на трибуне А, либо только на трибуне Б.
![]()
1 Это определение, как и предыдущее, распространяется на случай п высказываний (п > 2, п натуральное число).
Определение 5. Строгая, или
разделительная дизъюнкция — ![]() логическая операция, ставящая в
соответствие двум элементарным высказываниям новое высказывание, являющееся
истинным тогда и только тогда, когда ровно одно из двух высказываний является
истинным. Логическая операция разделительная дизъюнкция определяется следующей
таблицей истинности:
логическая операция, ставящая в
соответствие двум элементарным высказываниям новое высказывание, являющееся
истинным тогда и только тогда, когда ровно одно из двух высказываний является
истинным. Логическая операция разделительная дизъюнкция определяется следующей
таблицей истинности:
|
Р |
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
1 |
|
1 |
1 |
|
Вопрос. В сложном высказывании использована связка «или». Какая это Дизъюнкция: нестрогая или строгая?
Ответ. В логике связкам «либо» и «или» придается разное значение, однако в русском языке связку «или» иногда употребляют вместо связки «либо». Чтобы определить значение связки «или», нужно проанализировать содержание высказывания по смыслу. Например, анализ высказывания {Петя сиДит на трибуне А ИЛИ на трибуне Б} однозначно укажет на логическую операцию разделительная дизъюнкция, так как человек не может находить в двух разных местах одновременно.
3.2.4. Предложение, образованное из двух предложений, объединенных связкой «если ..., то ... » , в грамматике называется условным предложением, а в логике такое высказывание называется импликацией.
Импликацию мы используем тогда, когда хотим показать, что некоторое событие зависит от другого события. Например, пусть человек сказал: «Если завтра будет хорошая погоДа, то я пойду гулять» . Здесь р = {Завтра буДет хорошая погоДа} и q = {Я пойду гулять}. Ясно, что человек окажется лжецом лишь в том случае, если погода действительно окажется хорошей, а гулять он не пойдет. Если же погода будет плохой, то независимо от того, пойдет он гулять или нет, во лжи его нельзя обвинить: обещание пойти гулять он давал лишь при условии, что погода будет хорошей.
|
|
|
|
|
|
|
1 |
|
|
1 |
1 |
|
1 |
|
|
|
1 |
1 |
1 |
Мы видим, что импликация заведомо истинна, если условие р ложно. Другими словами, из неверного условия может следовать все, что угодно. Например, высказывание Если 2 > З, то крокодилы летают} является истинным.
Подавляющее число зависимостей между событиями можно описать с помощью импликации.
Пример 1. Истинным высказыванием {Если на каникулах мы поеДем в Петербург, то посетим Исаакиевский собор} мы утверждаем, что в случае приезда на каникулах в Петербург Исаакиевский собор мы посетим обязательно.
В соответствии с определением импликации истинны следующие высказывания:
а) Если 2 х 2 4, то через Смоленск протекает Днепр}.
б) {Если через Смоленск протекает Енисей, то 2 х 2 = 4}.
в) {Если через Смоленск протекает Енисей, то 2 х 2 = 5}.
г) {Если все ученики класса напишут контрольную работу по физике на отлично, то слоны в Африке живут}.
д) {Если через Смоленск протекает Енисей, то все ученики класса напишут контрольную работу по физике на отлично}.
Отметим, что высказывания г) и д) являются истинными импликациями и в том случае, если высказывание {все ученики класса напишут контрольную работу по физике на отлично} является истинным, и в том случае, если оно является ложным.
Следующие две импликации являются ложными, так как в них посылки истинны, а заключения ложны:
е) {Если 2 х 2 4, то через Смоленск протекает Енисей}.
ж) {Если через Смоленск протекает Днепр, то Луна сделана из теста).
Может показаться странным, что высказывание «Если А, то В» всегда истинно, если посылка (высказывание А) ложна. Но для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение.
Допустим, что 1 = 2, тогда и 2 = 1.
Складывая эти ра![]() венства, получим З = З, т. е. из ложной
посылки путем тождественных преобразований мы получили истинное высказывание.
венства, получим З = З, т. е. из ложной
посылки путем тождественных преобразований мы получили истинное высказывание.
Большинство математических теорем являются импликациями. Однако те импликации, в которых посылки (условия) и заключения (следствия) являются предложениями без взаимной (по существу) связи, не могут играть в науке важной роли. Они являются бесплодными предложениями, так как не ведут к выводам более глубокого содержания.
В математике ни одна теорема не является импликацией, в которой условие и заключение не были бы связаны по содержанию. Достаточно часто в математических теоремах импликации формулируются в виде только необходимого или только Достаточного условия.
3.2.5. Высказывание, образованное из двух высказываний при помощи связки «тогда и только тогда, когда», в логике называется эквивалентностью. Эквивалентность используется в тех случаях, когда необходимо выразить взаимную обусловленность. Например, сообщая:
{Я получу паспорт тогда и только тогДа, когДа мне исполнится 14 лет}, человек утверждает не только то, что после того, как ему исполнится 14 лет, он получит паспорт, но и то, что паспорт он сможет получить только после того, как ему исполнится 14 лет.
Определение 7. Эквивалентность — логическая операция, ставящая в соответствие двум элементарным высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Логическая операция эквивалентность задается следующей таблицей истинности:
|
|
|
|
|
0 |
|
1 |
|
0 |
1 |
|
|
1 |
|
|
|
1 |
1 |
1 |
Рассмотрим возможные значения сложного высказывания, являющегося эквивалентностью: {Учитель утвержДает, что 5 в четверти ученику он поставит тогДа и только тогда, когДа ученик получит 5 на зачете}.
1) Ученик получил 5 на зачете и 5 в четверти, т. е. учитель выполнил свое обещание, следовательно, высказывание является истинным.
2) Ученик не получил на зачете 5, и учитель не поставил ему 5 в четверти, т. е. учитель свое обещание сдержал, высказывание является истинным.
З) Ученик не получил на зачете 5, но учитель поставил ему 5 в четверти, т. е. учитель свое обещание не сдержал, высказывание является ложным.
4) Ученик получил на зачете 5, но учитель не поставил ему 5 в четверти, т. е. учитель свое обещание не сдержал, высказывание является ложным.
![]() В математических теоремах эквивалентность выракается
связкой «необходимо и достаточно» .
В математических теоремах эквивалентность выракается
связкой «необходимо и достаточно» .
3.2.6. Рассмотренные выше операции были двуместными
(бинарными), т. е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко применяется и одноместная (унарная) операция отрицание.
|
|
Р |
|
|
1 |
|
1 |
|
В русском языке для построения отрицания используется связка «неверно, что». Хотя связка «неверно, что» и не связывает двух каких-либо высказываний в одно, она трактуется логиками как логическая связка, поскольку, поставленная перед произвольным высказыванием, образует из него новое.
Пример 2. Отрицанием высказывания {У меня Дома есть компьютер} будет высказывание {Неверно, что у меня Дома есть компьютер} или, что в русском языке то же самое, {У меня Дома нет компьютера}.
Пример З. Отрицанием высказывания {Я не знаю корейского языка} будет высказывание {Неверно, что я не знаю корейского языња} или {Я знаю корейский язьж}.
Пример 4. Отрицанием высказывания {Все
юноши 11-х классов отличники} является высказывание {Неверно, что все юноши
11-х классов — отличники} или {Не все юноши 11-х классов отличники} или другими
словами, {Нењоторые юноши 11-х классов — не отличники). ![]()
На первый взгляд кажется, что построить отрицание к заданному высказыванию достаточно просто. Однако это не так.
Пример 5, Высказывание {Все юноши
11-х классов — не отличники} не является отрицанием высказывания {Все юноши
11-х классов отличники}. Объясняется это следующим образом. Высказывание {Все
юноши 11-х классов — отличники} ложно. Отрицанием к ложному высказыванию должно
быть высказывание, являющееся истинным. Но высказывание {Все юноши 11-х классов
![]() не
отличники} не является истинным, так как среди одиннадцатиклассников есть Какс
ОтлИЧНИКИ, так и не отличники.
не
отличники} не является истинным, так как среди одиннадцатиклассников есть Какс
ОтлИЧНИКИ, так и не отличники.
1) {На стоянке стоят не красные «Жигули»}; 2) {На стоянке стоит белый «МерсеДес»};
З) {Красные «Жигули» стоят не на стоянке}.
Попробуйте этот пример разобрать самостоятельно. 2
Проанализировав приведенные примеры, можно вывести полезное правило.
Правило построения отрицания к простому высказыванию
При построении отрицания к простому высказыванию либ используется речевой оборот «неверно, что», либо отрицание строится к сказуемому, тогда к сказуемому добавляется частица «не», при этом слово «все» заменяется на «некоторые» и наоборот.
В заключение приведем сводную таблицу
истинности для введенных логических операций. ![]()
|
|
|
|
|
p v q |
р Э Ч |
р ч |
р- ч |
|
О |
О |
1 |
|
|
|
1 |
1 |
|
О |
1 |
1 |
|
1 |
1 |
1 |
|
|
1 |
о |
0 |
|
1 |
1 |
|
|
|
1 |
1 |
0 |
1 |
1 |
|
1 |
1 |
Вопросы и задания
1.
В следующих высказываниях выделите простые, обозначив каждое их
них буквой; запишите с помощью букв и знаков логических операций каждое
составное высказы![]() вание .
вание .
а) Число 376 четное и трехзначное.
![]() б) Зимой дети катаются на коньках или на
лыжах.
б) Зимой дети катаются на коньках или на
лыжах.
в) Новый год мы встретим на даче либо на Красной площади.
г) Неверно, что Солнце движется вокруг Земли.
![]() д) Если 14 октября
будет солнечным, то зима будет теплой.
д) Если 14 октября
будет солнечным, то зима будет теплой.
![]()
![]()
![]()
![]()
ж) На уроке математики старшеклассники отвечали на вопросы учителя, а также писали самостоятельную работу.
з) Если вчера было воскресенье, то Дима вчера не был в школе и весь день гулял.
и) Если сумма цифр натурального числа
делится на З, то ![]() число делится на З.
число делится на З.
к) Число делится на З тогда и только тогда, когда сумма цифр числа делится на З.
2.
Ниже приведена таблица, левая колонка которой содержит основные
логические союзы (связки), с помощью ко![]() торых в естественном языке строятся
сложные высказывания. Заполните правую колонку таблицы названиями наиболее
подходящих логических операций.
торых в естественном языке строятся
сложные высказывания. Заполните правую колонку таблицы названиями наиболее
подходящих логических операций.![]()
|
|
|
|

З. Постройте отрицания следующих высказываний.
а) Сегодня в театре идет опера «Евгений Онегин».
б) Каждый охотник желает знать, где сидит фазан.
в) Число 1 есть простое число.
г) Число 1 составное .
д) Натуральные числа, оканчивающиеся цифрой О, являются простыми числами.
е) Неверно, что число З не является делителем числа 198.
ж) Коля решил все задания контрольной работы.
з) Неверно, что любое число, оканчивающееся цифрой 4, делится на 4.
и) Во всякой школе некоторые ученики интересуются спортом.
к) Некоторые млекопитающие не живут на суше.
4. ![]() Являются
ли отрицаниями друг друга следующие пары предложений?
Являются
ли отрицаниями друг друга следующие пары предложений?
а) Он мой друг. Он мой враг.
б) Большой дом. Небольшой дом.
в) Большой дом. Маленький дом.
![]()
5. Пусть р = Ине нравятся уроки математики}, а q = Ане нравятся уроки химии). Выразите следующие формулы на естественном языке.
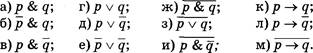
6. В математических теоремах импликация выражается не только связкой «если ..., то» . Высказывание «для того чтобы выполнялось А, достаточно, чтобы выполнялось В» соответствует импликации (В А). Запишите в символике алгебры логики импликацию «для того чтобы выполнялось А, необходимо, чтобы выполнялось В» .
S 3.3. Логические формулы. Законы алгебры логики
Математики под словом «алгебра» подразумевают науку, которая изучает некие объекты и операции над ними. Например, школьная алгебра (алгебра действительных чисел) изучает действительные числа и операции над ними. Предметом же нашего изучения являются высказывания, операции над ними, а также логические функции. В предыдущих параграфах для обозначения высказываний мы использовали буквы. Как и в алгебре действительных чисел, введем следующие определения.
Определение 9. Логической переменной
называется перемен![]() ная, значением которой может быть любое
высказывание. Логические переменные (далее «переменные») обозначаются
латинскими буквами, иногда снабженными индексами, как обычные алгебраические
переменные:
ная, значением которой может быть любое
высказывание. Логические переменные (далее «переменные») обозначаются
латинскими буквами, иногда снабженными индексами, как обычные алгебраические
переменные:
![]()
Определение 10. Логической формулой является:
1) любая логическая переменная, а также каждая из двух логических констант — О (ложь) и 1 (истина);
2) если А и В — формулы, то В и А*В — тоже формулы, где знак «*» означает любую из логических бинарных операций .
Формулой является, например, следующее выражение: (х & у) z. Каждой формуле при заданных значениях входящих в нее переменных приписывается одно из двух значений О или 1.
Определение 11. Формулы А и В, зависящие от одного и того же набора переменных Ч, ху х х , называют равносильными или эквивалентными, если на любом наборе значений переменных х 1 , ху х х они имеют одинаковые значения. Для обозначения равносильности формул используется знак равенства, например А = В.
В дальнейшем будет показано, что любую формулу можно преобразовать к равносильной ей, в которой используются только аксиоматически введенные операции &, v и отрицание.
Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел будем называть законами:
![]() 1) законы коммутативности
1) законы коммутативности
![]()
2) законы ассоциативности
![]()
З) законы поглощения (нуля и единицы)
![]()
4) законы дистрибутивности
![]()
5) закон противоречия
![]()
6) закон исключенного третьего
![]()
7)
законы идемпотентности ![]() х, x v x = х;
х, x v x = х;
8) закон двойного отрицания
9) законы де Моргана
![]()
10) законы поглощения
![]()
Любой из этих законов может быть легко доказан с помощью таблиц истинности.
Пример 7. Докажем первый закон де Моргана с использованием таблиц истинности. Построим таблицу истинности для левой и правой частей закона.
![]()
1
От латинских слов idem — тот же самый и potens —
сильный; дословно ![]() равносильный.
равносильный.
|
х |
У |
х&у |
|
|
|
x vy |
|
о |
О |
|
1 |
1 |
1 |
1 |
|
о |
1 |
|
1 |
1 |
|
1 |
|
1 |
|
|
1 |
О |
1 |
1 |
|
1 |
1 |
|
о |
О |
о |
О |
Так как результирующие столбцы совпали, то формулы, стоящие в левой и правой частях закона, равносильны. О Любой из законов алгебры логики может быть доказан путем логических рассуждений.
Пример 8. Докажем первый закон поглощения
х v (х у) = х путем логических рассуждений. Для этого достаточно ![]() показать,
что если правая часть истинна, то и левая часть истинна, и что если левая часть
истинна, то и правая часть истинна.
показать,
что если правая часть истинна, то и левая часть истинна, и что если левая часть
истинна, то и правая часть истинна.
Еще одним способом вывода законов являются тожДественные преобразования.
Пример 9. Первый закон поглощения можно вывести при помощи законов поглощения единицы и дистрибутивности:
![]()
Определение 12. Формула А называется тавтологией (или тождественно истинной), если она истинна при любых значениях своих переменных.
Пример 10. Тавтологией является формула х х, выражающая закон исключенного третьего.
![]() В алгебре логики дизъюнкцию еще называют
логическим сложением, а конъюнкцию — логическим умножением. Если продолжать
аналогию между логическими и арифметическими операциями, то операция отрицания
по некоторым характеристикам аналогична унарному минусу.
В алгебре логики дизъюнкцию еще называют
логическим сложением, а конъюнкцию — логическим умножением. Если продолжать
аналогию между логическими и арифметическими операциями, то операция отрицания
по некоторым характеристикам аналогична унарному минусу.
Для логических операций установлен следующий порядок вычислений: 1) отрицание; 2) конъюнкция; З) дизъюнкция (строгая и нестрогая); 4) импликация и эквивалентность.
Поэтому при записи логических формул с
использованием этих операций скобки требуется расставлять толь![]() ко для того,
чтобы изменить порядок выполнения операций, фиксированный по умолчанию.
Например, выражение х v у & z трактуется как х х.' (у & г).
ко для того,
чтобы изменить порядок выполнения операций, фиксированный по умолчанию.
Например, выражение х v у & z трактуется как х х.' (у & г).
Вопросы и задания
1. Какие из рассмотренных логических законов аналогичны законам алгебры чисел, а какие нет?
2. Докажите второй закон де Моргана с помощью таблиц истинности.
З. Рассмотрите два сложных высказывания:
![]() Е 1 = {если одно
слагаемое делится на З и сумма делится на З, то и другое слагаемое делится на
3};
Е 1 = {если одно
слагаемое делится на З и сумма делится на З, то и другое слагаемое делится на
3};
![]()
![]() Е2 = {если одно слагаемое делится на З, а другое не
делится на З, то сумма не делится на 3}.
Е2 = {если одно слагаемое делится на З, а другое не
делится на З, то сумма не делится на 3}.
Формализуйте эти высказывания, постройте
таблицы истинности для каждой из полученных формул и убеди![]() тесь, что
результирующие столбцы совпадают.
тесь, что
результирующие столбцы совпадают.
4. Формализуйте следующие высказывания и постройте для них таблицы истинности:
![]() = {если все стороны четырехугольника
равны и один из его углов прямой, то этот четырехугольник является
= {если все стороны четырехугольника
равны и один из его углов прямой, то этот четырехугольник является
квадратом};
F2 = {если все стороны четырехугольника равны, а он не является квадратом, то один из его углов не является прямым}.
5. Для операций импликации, эквивалентности и разделительной дизъюнкции также может быть сформулирован ряд важных свойств. В частности, каждая из этих операций может быть выражена через конъюнкцию, дизъюнкцик) и отрицание. Убедитесь в этом, доказав самостоятельно следующие соотношения:
![]()
б) а — Ь = а & b v a 8' Ь;
6. 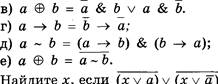 Найдите
х, если (х а) (х v б) = Ь.
Найдите
х, если (х а) (х v б) = Ь.
7. Какие из следующих формул являются тавтологиями?
8. Логическая
формула называется тождественно ложной, если она принимает значение О на всех
наборах входящих в ![]() нее переменных. Упростите формулу а
& (а —> Ь) & (а Ь) и покажите, что она тождественно ложна.
нее переменных. Упростите формулу а
& (а —> Ь) & (а Ь) и покажите, что она тождественно ложна.
S 3.4. Методы решения логических задач
Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.
Формальный способ решения логических задач
1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
2. Записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций.
З. Составить единое логическое выражение для всех требований задачи.
4. Используя законы алгебры логики, попытаться упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения.
5. Выбрать решение — набор значений простых высказываний, при котором построенное логическое выражение является истинным.
6. Проверить, удовлетворяет ли полученное решение условию задачи.
Рассмотрим, как можно использовать данный способ для решения задач.
Пример 11. Задача «Уроки логики».
На вопрос, кто из трех учащихся изучал
логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно,
что если изучал третий, то изучал и ![]() второй». Кто из учащихся изучал логику?
второй». Кто из учащихся изучал логику?
Решение. Обозначим через Р 1 , Р 2 , Рз
высказывания, состоящие в том, что соответственно первый, второй, третий
учащийся изучали логику. Из условия задачи следует истинность
высказывания (Ц ![]() (Рз —» Ц).
(Рз —» Ц).
= ![]()
Высказывание Р 2 & Р 2 ложно, а следовательно, ложно и высказывание Р 2 & Рз & Р . Поэтому должно быть истинным высказывание Р & Р & Р 2 , а это означает, что логику изучал третий учащийся, а первый и второй не изучали.
Для решения следующей задачи составим логическое выражение, удовлетворяющее всем условиям, затем заполним для него таблицу истинности. Анализ полученной таблицы истинности позволит получить требуемый результат.
Пример 12. Задача «Кто виноват?»
По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено:
1) если Иванов не виновен или Петров виновен, то Сидоров виновен;
![]() 2) если Иванов не
виновен, то Сидоров не виновен. Виновен ли Иванов?
2) если Иванов не
виновен, то Сидоров не виновен. Виновен ли Иванов?
Решение. Рассмотрим простые высказывания:
![]() {Иванов виновен), В = {Петров виновен),
{Иванов виновен), В = {Петров виновен),
С = {Сидоров виновен).
Запишем на языке алгебры логики факты, установленные следствием:
![]()
|
|
в |
|
|
|
О |
о |
О |
о |
|
О |
о |
1 |
|
|
О |
1 |
о |
О |
|
О |
1 |
1 |
|
|
1 |
о |
О |
1 |
|
1 |
о |
1 |
1 |
|
1 |
1 |
о |
о |
|
1 |
1 |
1 |
1 |
Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание 1' истинно. Для этого необходимо проанализировать все строки таблицы истинности, где = 1. И если хотя бы в одном из таких случаев А = О (Иванов не виновен), то у следствия недостаточно фактов для того, чтобы обвинить Иванова в преступлении.
Анализ таблицы показывает, что высказывание F истинно только в тех случаях, когда А истинно, т. е. Иванов в ограблении виновен.
Иногда, для того чтобы решить задачу, нет необходимости составлять единое логическое выражение, удовлетворяющее всем условиям задачи, достаточно построить таблицу истинности, отражающую каждое условие задачи, и проанализировать ее.
Пример 13. Решим текстовую задачу, построив совместную таблицу истинности для условий задачи и пранализировав ее.
Три подразделения А, В, С торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения:
1) А получит максимальную прибыль только тогда, когда получат максимальную прибыль В и С,
2) Либо А и С получат максимальную прибыль одновременно, либо одновременно не получат,
З) Для того чтобы подразделение С получило максимальную прибыль, необходимо, чтобы и В получило максимальную прибыль.
По завершении года оказалось, что одно из трех предположений ложно, а остальные два истинны. Какие из названных подразделений получили максимальную прибыль?
Решение. Рассмотрим простые
высказывания: А = {А получит максимальную прибыль}, ![]()
В = {В получит максимальную прибыль},
С = {С получит максимальную прибыль}.
![]()
Составим таблицу истинности для![]()
|
|
|
о |
|
|
|
|
|
о |
1 |
1 |
1 |
|
|
о |
о |
1 |
1 |
|
|
|
о |
1 |
о |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
1 |
о |
о |
о |
о |
1 |
|
1 |
о |
1 |
о |
1 |
|
|
1 |
1 |
|
о |
о |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
Теперь вспомним, что один из прогнозов Е 1 , Е2 , Ез оказался ложным, а остальные два — истинными. Эта ситуация соответствует четвертой строке таблицы. Ответ: В и С получат максимальную прибыль.
Если число простых высказываний в решаемой задаче больше трех, то таблица истинности насчитывает 16, 32 и более строк, заполнять ее вручную достаточно трудоемко. Умение заполнять таблицу истинности с привлечением компьютера помогает преодолеть это неудобство.
Вопросы и задания
1. Задача «Валютные махинации» .
В нарушении правил обмена валюты подозреваются четыре работника банка — Антипов (А), Борисов (В), Цветков (С) и Дмитриев (D). Известно:
1) если А нарушил правила обмена валюты, то и В нарушил;
2) если В нарушил, то и С нарушил или А не нарушил; З) если D не нарушил, то А нарушил, а С не нарушил; 4) если D нарушил, то и А нарушил.
Кто из подозреваемых нарушил правила обмена валюты?
2. Задача «Пятеро друзей».
1) если А приходит вместе с D, то лт должен присутствовать обязательно;
2) если D отсутствует, то лт должен быть, а пусть не приходит;
З) А и не могут одновременно ни присутствовать, ни отсутствовать;
4) если придет D, то G пусть не приходит;
5) если N отсутствует, то D должен присутствовать, но это в том случае, если не присутствует У; если же и V присутствует при отсутствии N, то D приходить не должен, а G должен прийти» .
В каком составе друзья смогут прийти на занятия кружка?
З. Решите логическую задачу, используя только алгебраические преобразования логических формул.
Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники скрылись на синем «Бьюике»; Джонс сказал, что это был черный «Крайслер», а Смит утверждал, что это был «Форд Мустанг» и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет. Какого цвета и какой марки был автомобиль?
4. Решите логическую задачу, используя только алгебраические преобразования логических формул.
5. Напишите программу, которая строит таблицу истинности по заданной логической формуле, Используйте для этого известный вам язык программирования или воспользуйтесь электронной таблицей.
S 3.5. Алгебра переключательных схем
Одним из практических применений алгебры логики является область параллельно-последовательных переключательных схем.
Определение 13. Переключательная схема — это изображение некоторого устройства, содержащего только двухпозиционные переключатели, которые могут находиться в одном из двух состояний: замкнутое (ток проходит) или разомкнутое (ток не проходит).
Очевидно, что состояние переключателя
можно кодироватъ числами 1 и О. Большинство переключательных схем можно разбить
на участки из последовательно или параллельно соединенных переключателей.
Каждому переключателю поставим в соответствие логическую переменную,
принимающую значение «истина» тогда, когда переключатель замкнут, и «ложь»,
если переключа![]() тель разомкнут. На схемах переключатели
будем обозначатъ теми же буквами, что и соответствующие им переменные.
тель разомкнут. На схемах переключатели
будем обозначатъ теми же буквами, что и соответствующие им переменные.
При описании переключательных схем будем придерживаться следующих соглашений:
1. Все переключатели, работающие так, что они всегда либо одновременно замкнуты, либо одновременно разомкнуты, обозначаются одной и той же буквой.
2. Переключателям, соединенным параллельно, поставим в соответствие операцию дизъюнкции: ток в этой цепи (рис. 3.1, а) будет протекать или при замкнутом переключателе А, или при замкнутом переключателе В, или при замкнутых переключателях А и В одновременно.
|
|
|
Рис. 3.1
З. Переключателям, соединенным последовательно, поставим в
соответствие операцию конъюнкции: ток в ![]() цепи (рис. 3.1, б)
потечет только тогда, когда замкнут переключатель А и замкнут переключатель В.
цепи (рис. 3.1, б)
потечет только тогда, когда замкнут переключатель А и замкнут переключатель В.
4. Два переключателя, работающие так, что один из них замкнут, когда другой њазомкнут, и наоборот, описываются формулами А ИА соответственно (рис. 3.1, в).
Прочитать переключательную схему — значит определить, протекает по ней ток или нет при указанных а состояниях переключателей.
Определение 14. Две схемы, содержащие одни и те же переключатели А, В, будем считать равными, если при одном и том же состоянии переключателей обе схемы одновременно пропускают или не пропускают ток. Из двух равных схем более простой будем считать ту, которая содержит меньше переключателей.
Каждой переключательной схеме можно поставить в соответствие формулу, истинную тогда и только тогда,
когда схема проводит ток. В алгебре переключательных схем выполняются все законы алгебры логики. В этом достаточно просто убедиться, если построить и прочитать соответствующие этим законам схемы, а затем сравнить столбец состояния каждой схемы с результирующим столбцом таблицы истинности для соответствующей логической формулы.
Пример 14. Составим формулу для схемы, изображенной на рисунке.
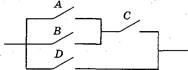
![]()
Синтез переключательной схемы — это разработка схемы, условия работы которой заданы таблицей истинности или словесным описанием. Упрощение (минимизация) переключательной схемы сводится к упрощению соответствующей ей формулы на основании законов алгебры логики.
![]()
Вопросы и задания
1. Каким
образом интерпретируются элементы переключательных схем с помощью объектов и
операций алгебры ![]() логики? Заполните следующую таблицу:
логики? Заполните следующую таблицу:
|
|
|
|
2. Комиссия состоит из трех рядовых членов и председателя. Постройте электрическую цепь для тайного голосования, если оно производится следующим образом: каждый член комиссии при голосовании «за» нажимает кнопку. Лампочка зажигается в случаях, если предложение набрало большинство голосов или число голосов «за» и «против» равное, но за предложение «за» подан голос председателя.
З. Можно ли изображенную на рисунке электрическую цепь заменить более простой схемой, соответствующей форму-
![]()
х
|
|
|
||||
|
|
|||||
|
|
х |
|
|
||
|
|
|
||||
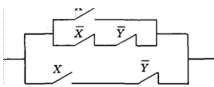
S 3.6. Булевы функции
Как было сказано выше, значение логической формулы определяется заданными значениями входящих в формулу переменных. Тем самым каждая формула может рассматриваться как способ задания функции алгебры логики.
![]() Определение 15. Логической (булевой) функцией называют
функцию
Определение 15. Логической (булевой) функцией называют
функцию ![]() ), аргументы которой хр х2, х
(независимые переменные) и сама функция (зависимая переменная) принимают
значения О или 1. Логические функции могут быть заданы табличным способом или
аналитически в виде соответствующих формул.
), аргументы которой хр х2, х
(независимые переменные) и сама функция (зависимая переменная) принимают
значения О или 1. Логические функции могут быть заданы табличным способом или
аналитически в виде соответствующих формул.
В общем случае булева функция от п
аргументов определяется как отображение {О, —> {0, 1}. Обычно совокупность
значений п аргументов интерпретируют как строку нулей и единиц (бинарную
строку) длины п. Существует ровно 2 п различных бинарных строк длины
п. Так как на каждой такой строке некая функция может принимать значение О или
1, то общее количество различных булевых функций от п аргументов равно 2 ![]()
![]() Для п = 2 существует 16 различных булевых функций.
Для п = 2 существует 16 различных булевых функций.
Рассмотрим их подробно.

![]() 1 константа
«ложь» (f(x, у) О);
1 константа
«ложь» (f(x, у) О);
![]() — стрелка Пирса
(отрицание дизъюнкции, ИЛИ-НЕ);
— стрелка Пирса
(отрицание дизъюнкции, ИЛИ-НЕ); ![]() эквивалентность;
эквивалентность;
— отрицание второго аргумента; — обратная импликация; отрицание первого аргумента; 14 импликация; f15(x, у) — х у — штрих Шеффера 2 (отрицание конъюнкции, И-НЕ);
![]() —
константа «истина» (f(x, у) 1).
—
константа «истина» (f(x, у) 1).
1
Ч. С. пирс— американский философ, логик, математик; исследовал свойства функции х у.
2 Х. М. Шеффер — американский логик и математик; указал полноту функции
Функции, выраженные с использованием одной логической операции, называются по имени этой логической операции. Например, f2(x, у) = х & у — конъюнкция.
С увеличением числа аргументов
количество логических функций резко возрастает. Для трех переменных ![]() существует
256 различных булевых функций. Для четырех переменных — уже 65 536 функций и т.
д. Пугаться резкого увеличения количества функций не следует, как будет
показано ниже, при необходимости любая булева
существует
256 различных булевых функций. Для четырех переменных — уже 65 536 функций и т.
д. Пугаться резкого увеличения количества функций не следует, как будет
показано ниже, при необходимости любая булева ![]() функция, может быть
выражена только, например, через &, v и отрицание.
функция, может быть
выражена только, например, через &, v и отрицание.
Вопросы и задания![]()
![]() 1. Сколько существует
логических функций одной переменной?
1. Сколько существует
логических функций одной переменной?
![]() 2. Составьте сводную
таблицу всех логических функций одной переменной. Запишите аналитические
выражения этих функций.
2. Составьте сводную
таблицу всех логических функций одной переменной. Запишите аналитические
выражения этих функций.
![]()
![]()
![]()
S 3.7. Канонические формы логических
формул. ![]() Теорема о СДНФ
Теорема о СДНФ![]()
![]() Всякая логическая формула определяет
некоторую буле
Всякая логическая формула определяет
некоторую буле![]() функцию. В то же время ясно, что для
всякой буле
функцию. В то же время ясно, что для
всякой буле![]() вой функции можно записать бесконечно
много формул, ее представляющих (см. задание З к S 3.6). Действительно, если
имеется хотя бы одна формула, выражающая
вой функции можно записать бесконечно
много формул, ее представляющих (см. задание З к S 3.6). Действительно, если
имеется хотя бы одна формула, выражающая ![]() булеву функцию, то,
используя тождественные преобразования, можно изменить эту формулу, построив
сколь
булеву функцию, то,
используя тождественные преобразования, можно изменить эту формулу, построив
сколь ![]() угодно сложную равносильную формулу.
угодно сложную равносильную формулу. ![]()
Одна из основных задач алгебры логики —
нахождение канонических форм (т. е. формул, построенных по определенному
правилу, канону), а также наиболее простых формул, представляющих булевы
функции. ![]()
Определение 16. Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.
Среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными.
![]() Особую роль в алгебре логики играют классы ДИЗЪюнктивных и
конъюнктивных совершенных норлшЛЬНЫХ форм. В их основе лежат понятия элементарной
дизъюнкции и элементарной конъюнкции.
Особую роль в алгебре логики играют классы ДИЗЪюнктивных и
конъюнктивных совершенных норлшЛЬНЫХ форм. В их основе лежат понятия элементарной
дизъюнкции и элементарной конъюнкции.
Пример 15. Формулы х х & хз, х & хз & х 1 & хз являются элементарными конъюнкциями; первые две из них — одночленными.
Определение 18. Формула называется
Дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией
неповторяющихся элементарных конъюнкций. ДНФ записываются в виде „41 v А2 х.! А
, где каждое А. ![]()
элементарная конъюнкция.
Пример 16. Приведем две дизъюнктивные
нормальные формы: &хз, Х2 v vx![]()
Определение 19. Формула А от К переменных называется совершенной Дизъюнктивной нормальной формой (СДНФ), если:
1) А является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция К переменных хр ху ..., ХК , причем на i-M месте ЭТОЙ КОНЪЮНКЦИИ стоит либо переменная х., либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Задание. Даны формулы А = х1 & х2
v .х1 & х2', В = х1 v х2 & хз и С = х1 & х2 v х2 & х2.
ОпреДелить, являются ли они СДНФ двух переменных.![]()
Решение. Формула А является СДНФ двух переменных. Формулы В и С не являются СДНФ. Формула В зависит от трех переменных, но количество переменных в элементарных конъюнкциях меньше трех. В формуле С переменная х2 дважды входит в одну и ту же элементарную конъюнкцию.
![]() Совершенная дизъюнктивная нормальная форма представляет
собой формулу, построенную по строго определенным правилам с точностью до
порядка следования элементарных конъюнкций (дизъюнктивных членов) в ней. Она
является примером однозначного представления булевой функции в виде формульной
(алгебраической) записи.
Совершенная дизъюнктивная нормальная форма представляет
собой формулу, построенную по строго определенным правилам с точностью до
порядка следования элементарных конъюнкций (дизъюнктивных членов) в ней. Она
является примером однозначного представления булевой функции в виде формульной
(алгебраической) записи.
Пример 17. Приведем три элементарные дизъюнкции:
![]()
Определение 21. Формула называется конъюнктивной нормальноЙ формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций. КНФ записываются в виде „41 &А & ... & А , где каждое А. — элементарная дизъюнкция.
Пример 18. Формулы
![]() , ху Х2 V Xz, (Х2
Х1) & ХЗ, (X2V Х2) & (Х1 V Х1) являются конъюнктивными нормальными
формами. 2
, ху Х2 V Xz, (Х2
Х1) & ХЗ, (X2V Х2) & (Х1 V Х1) являются конъюнктивными нормальными
формами. 2
Определение 22. Формула А от К переменных называется со![]() вершенной КОНЪЮНКТИВНОЙ нормальной формой (СКНФ), если:
вершенной КОНЪЮНКТИВНОЙ нормальной формой (СКНФ), если:
1)
А является КНФ, в которой каждая элементарная дизъюнкция есть
дизъюнкция К переменных ![]() х причем на i-M месте этой дизъюнкции
стоит либо переменная х., либо ее отрицание;
х причем на i-M месте этой дизъюнкции
стоит либо переменная х., либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.
Задание. Даны формулы А = (х1 х2) & (х1 v х2) и В = (х1 v х1) & (х2 хз). ОпреДелить, являются ли они СКНФ.
Решение. Формула А является СКНФ, а формула В не является СКНФ, поскольку переменная х1 дважды входит в первый конъюнктивный член, кроме того, количество переменных в каждой элементарной дизъюнкции меньше трех, в то время как формула зависит от трех переменных.
Вопрос. Всякую ли логическую функцию можно преДставить в одной из рассмотренных канонических совершенных форм?
Ответ. Да, любую булеву функцию, не равную тождественно О или 1, можно представить в виде СДНФ или СКНФ. Для обоснования этого утверждения ниже будут доказаны соответствующие теоремы.
Доказательство. Сначала докажем, что
для всякой булевой функции f от п переменных выполняется соотношение: ![]() хп)
f(xp Х2, .. ., О, v ..ti & f(xp х,г,
хп)
f(xp Х2, .. ., О, v ..ti & f(xp х,г,
где Xi — любая из п переменных.
Формулу (3.1) легко получить, последовательно подставляя вместо переменной х. все ее возможные значения (ноль и единицу):
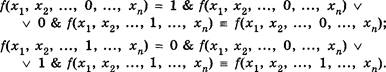
Соотношение (3.1) позволяет «выносить» переменную х. за знак функции. Последовательно вынося х 1 , , ..., ...Еп за знак функции f, мы получим следующую формулу:

Так как применение преобразования (3.1) к каждой из переменных увеличивает количество дизъюнктивных членов в два раза, то для функции п переменных в формуле (3.2) мы имеем дизъюнктивных членов. Причем каждый из них соответствует значению функции на одном из 2 п возможных наборов значений п переменных. Если на некотором наборе = О, то весь соответствующий дизъюнктивный член в (3.2) также равен О, и в представлении данной функции он фактически не нужен. Если же f = 1, то в соответствующем дизъюнктивном члене само значение функции можно опустить. В результате для произвольной булевой функции f мы получили формулу, состоящую из п-членных попарно различных элементарных конъюнкций, объединенных дизъюнкциями, т. е. искомая СДНФ построена. Теорема Доказана.
![]() На основании теоремы 1 можно предложить
следующий алгоритм построения СДНФ по таблице истинности функции f.
На основании теоремы 1 можно предложить
следующий алгоритм построения СДНФ по таблице истинности функции f.
Алгоритм построения СДНФ по таблице истинности
1. В таблице истинности отмечаем наборы переменных, на которых значение функции равно единице.
2. Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае ее отрицание.
З. Все полученные конъюнкции связываем операциями дизъюнкции.
Следствие. Для любой формулы можно найти равносильную ей ДНФ.
Доказательство. Если булева функция не равна тождественно нулю, то, согласно доказанной теореме 1, можно построить СДНФ, ее реализующую. Построенная СДНФ является одной из искомых ДНФ. Если же данная формула равна тождественно нулю, то в качестве искомой ДНФ можно взять, например, х 1 & х
![]()
Аналогично теореме 1 доказывается следующая теорема.
Теорема 2. Пусть f(x х![]() —
булева функция п переменных, не равная тождественно единице. Тогда сущест-
—
булева функция п переменных, не равная тождественно единице. Тогда сущест- ![]() вует
совершенная конъюнктивная нормальная форма, выражающая функцию f.
вует
совершенная конъюнктивная нормальная форма, выражающая функцию f.
На основании теоремы 2 можно предложить
следую![]() щий алгоритм построения СЕНФ по таблице
истинности функции f.
щий алгоритм построения СЕНФ по таблице
истинности функции f.
Алгоритм построения СКНФ по таблице истинности
1. В таблице истинности отмечаем наборы переменных, на которых значение функции f равно нулю.
2.
З. Все полученные дизъюнкции связываем операциями конъюнкции.
Следствие. Для любой формулы можно найти равносильную ей КНФ.
Доказательство. Если булева функция не равна тождественно единице, то, согласно доказанной теореме 2, можно построить СКНФ, ее реализующую. Построенная СКНФ является одной из искомых КНФ. Если же данная формула равна тождественно единице, то в качестве искомой КНФ можно взять, например, х 1 v х1'
![]() Из алгоритмов построения СДНФ и СКНФ следует, что если на
большей части наборов значений переменных функция равна О, то для получения ее
формулы проще построить СДНФ, в противном случае
Из алгоритмов построения СДНФ и СКНФ следует, что если на
большей части наборов значений переменных функция равна О, то для получения ее
формулы проще построить СДНФ, в противном случае ![]() СКНФ.
СКНФ.
Пример 19. Требуется построить формулу для функции f(xp х 2 , хз), заданной таблицей истинности:
|
|
|
ХЗ |
f(X1, Х2, ХЗ) |
|
о О о о 1 1 1 1 |
о О 1 1 О 1 1 |
о 1 1 О 1 о 1 |
1 1 1 о |
Используя описанный выше алгоритм, построим для нее СДНФ:
f(xv х 2 , хз) = х 1 & х 2 & х з м х 1 & х2 & хз v х 2 & хз.
|
|
Х 2 |
f( X 1' Х 2) |
Х 2 |
|
о о 1 1 |
о 1 1 |
1 1 1 |
|
Так как в таблице истинности только один
набор переменных, на котором функция принимает значение О, то ![]() проще
построить СКНФ.
проще
построить СКНФ.
Ответ: х2) = —> х2 = .х1 х2.
Вопросы и задания
1. Приведите примеры нескольких формул, представляющих собой СДНФ.
2. Приведите примеры нескольких формул, представляющих собой СКНФ.
З. По заданной таблице истинности найдите аналитическое представление логических функций f1 и fz:
|
|
|
|
|
|
|
ложь |
ложь |
ложь |
ложь |
ложь |
|
ложь |
ложь |
ИСТИНА |
ложь |
ИСТИНА |
|
ложь |
ИСТИНА |
ложь |
ИСТИНА |
ложь |
|
ложь |
ИСТИНА |
ИСТИНА |
ИСТИНА |
ИСТИНА |
|
ИСТИНА |
ложь |
ложь |
ложь |
ИСТИНА |
|
ИСТИНА |
ложь |
ИСТИНА |
ИСТИНА |
ИСТИНА |
|
ИСТИНА |
ИСТИНА |
ложь |
ложь |
ложь |
|
ИСТИНА |
ИСТИНА |
ИСТИНА |
ИСТИНА |
ложь |
Проверку произведите с помощью электронной таблицы.
4. С помощью отрицания, дизъюнкции и конъюнкции постройте наиболее простое аналитическое представление для функций эквивалентность и разделительная дизъюнкция.
5. Не используя таблицы истинности, постройте СДНФ и СКНФ, выражающие следующие функции:
1) f(xp .t2, хз), равную 1 тогда и только тогда, когда большинство переменных равно 1;
2) Ах 1 , ху хз, х4), равную 1 тогда и только тогда, когда х + х2 + хз + х З. Здесь имеется в виду обычная алгебраическая сумма.
6. Не используя таблицу истинности, преобразуйте в СДНФ следующую функцию:
f(xp хг, хз) = х1 & .х2 х 1 & хз.
7. Самостоятельно проведите доказательство теоремы 2.
8.
а) f(x) — 1;
![]() б) f(x) —
б) f(x) —
в) f(x,
г) f(x,
д) f(x,
е) f(x,
ж) f(x, у, г)
S 3.8. Минимизация булевых функций в классе
дизъюнктивных нормальных форм
Результаты, поля.тченные в предыдущем параграфе, имеют
большое прикладное значение при проектировании вычислительной техники. Как
известно, информация хранится и обрабатывается компьютерами в двоичном виде, т.
е. в виде последовательностей нулей и единиц. Для любой операции (например,
сложения чисел) исход![]() ными данными и результатами являются
последовательности нулей и единиц. Таким образом, фактически происходит
вычисление значений булевых функций (возможно, очень сложных, с большим
количествомпеременных). Теоремы 1 и 2 говорят о том, что любую булеву функцию
можно записать в виде формулы с использованием операций & и v (в виде СДНФ
или СКНФ), причем сделать это можно по единому универсальному алгоритму.
Следовательно, если у нас имеются элект
ными данными и результатами являются
последовательности нулей и единиц. Таким образом, фактически происходит
вычисление значений булевых функций (возможно, очень сложных, с большим
количествомпеременных). Теоремы 1 и 2 говорят о том, что любую булеву функцию
можно записать в виде формулы с использованием операций & и v (в виде СДНФ
или СКНФ), причем сделать это можно по единому универсальному алгоритму.
Следовательно, если у нас имеются элект![]() ронные логические
элементы (вентили) [3] , реализующие
ронные логические
элементы (вентили) [3] , реализующие ![]() операции
НЕ, И, ИЛИ, то, взяв достаточно много таких
операции
НЕ, И, ИЛИ, то, взяв достаточно много таких ![]() элементов и соединив
их определенным образом, мы можем построить машину, выполняющую заданный набор
действий над двоичными данными.
элементов и соединив
их определенным образом, мы можем построить машину, выполняющую заданный набор
действий над двоичными данными.
Определение 23. Дизъюнктивная
нормальная форма называется минимальной, если она содержит наименьшее общее ![]() число
вхождений переменных по сравнению со всеми равносильными ей ДНФ. Процесс
нахождения минимальной ДНФ называется минимизацией в классе ДНФ.
число
вхождений переменных по сравнению со всеми равносильными ей ДНФ. Процесс
нахождения минимальной ДНФ называется минимизацией в классе ДНФ.
Строить минимальные ДНФ из СДНФ можно разными способами, например используя тождественные преобразования.
Пример 21. Используя закон дистрибутивности и закон поглощения, выполним минимизацию ДНФ х & х2 v & х •
![]()
К сожалению, для нахождения минимальной ДНФ необходимо перебрать все возможные способы применения основных законов алгебры логики к исходной формуле. Для функций от большого числа переменных этот процесс оказывается слишком трудоемким, даже если проводить его с использованием компьютера.
Более эффективным способом нахождения минимальных ДНФ является метод минимизирующих карт.
Для булевой функции п переменных составим следующую таблицу (карту):

![]()
Предположим, что конъюнкция из последнего столбца К-й строки таблицы не входит в СДНФ, выражающую функцию f(xp ху х ), тогда любая конъюнкция К-й строки не входит ни в какую ДНФ, выражающую функцию f. Докажем это. Действительно, если конъюнкция не входит в СДНФ, выражающую функцию f, то, согласно алгоритму построения СДНФ, значение функции на этом наборе равно О. Если какая-то конъюнкция К-й строки вошла в некоторую ДНФ функции f, то на этом наборе функция должна быть равна единице. Мы получили противоречие с первоначальным предположением. Используя доказанное утверждение, можно предложить следующий способ построения минимальной ДНФ по минимизирующей карте.
Способ минимизации ДНФ методом минимизирующих карт
1. Вычеркнем из таблицы (минимизирующей карты) все строки, в которых конъюнкция последнего столбца не входит в СДНФ функции f.
2. Конъюнкции «вычеркнутых строк» вычеркнем во всех остальных строках таблицы.
З. Если в строке остались конъюнкции с различным числом сомножителей, то конъюнкции с не минимальным числом сомножителей оставляем только тогда, когда они встречаются в других строках.
4. Отметим конъюнкции, оставшиеся единственными на строке. Вычеркнем строки, в которых присутствуют такие же конъюнкции.
5. Всеми возможными способами выберем из каждой строки по одной конъюнкции (из оставшихся) и составим для каждого случая ДНФ.
6. Из всех построенных ДНФ выберем минимальную. Заметим, что мы должны выполнить перебор различных ДНФ для нахождения минимальной из них. Однако в данном случае число вариантов перебора, как правило, существенно меньше вариантов перебора равносильных ДНФ или способов сокращения СДНФ.
Пример 22. Пусть требуется минимизировать функцию f(x, у, г) = .Ч.Х2хз х1х2хз v .чх,гхз v х 1Х2Хз.
Составим минимизирующую карту для функции трех переменных. Отметим знаком «*» не вошедшие в СДНФ строки.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После действий в соответствии с п. 1—3 в таблице останутся конъюнкции, находящиеся в выделенных ячейках таблицы. Выполнив п. 4—6, получим минимальную ДНФ: ХIХз v Х2Хз.
Практические задания
1. Постройте отрицание к сложному высказыванию на русском языке. (В S 1.3 было показано, как непросто построить отрицание к простым высказываниям.) Возможный способ выполнения задания:
1) выделите простые высказывания и обозначьте их буквами;
2) запишите исходное предложение на языке алгебры логики, т. е. в виде логической формулы;
4) запишите таблицу значений противоположного по смыслу выражения;
5) восстановите по ней искомое логическое выражение
(например, в виде СДНФ или СКНФ);
6) если вы получили искомую формулу в виде СДНФ, то минимизируйте ее;
7) запишите на русском языке высказывание, соответствующее полученному выражению. Варианты задания
а) Если центральные углы равны, то и соответствующие им дуги равны, а если соответствующие центральным углам дуги равны, то и центральные углы равны.
б) Если две плоскости взаимно перпендикулярны и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, то этот перпендикуляр весь лежит в этой плоскости.
в) Если стороны одного угла соответственно перпендикулярны сторонам другого угла, то такие углы или равны, или в сумме составляют два прямых.
г) Если пирамида пересечена плоскостью, параллельной основанию, то в сечении получается многоугольник, подобный основанию.
д) Для того чтобы оплатить проезд в общественном транспорте, необходимо иметь некоторую сумму денег и достаточно иметь 100 руб.
![]() е) Из того, что некоторая ломаная,
вписанная в одну окружность и описанная около другой окружности, замкнулась,
следует, что и любая такая ломаная замкнется, а из того, что некоторая подобная
ломаная
е) Из того, что некоторая ломаная,
вписанная в одну окружность и описанная около другой окружности, замкнулась,
следует, что и любая такая ломаная замкнется, а из того, что некоторая подобная
ломаная ![]() не замкнулась, следует, что и любая
такая ломаная
не замкнулась, следует, что и любая
такая ломаная ![]() не замкнется.
не замкнется. ![]()
2. По выданной вам таблице истинности булевой функции постройте СДНФ и найдите для нее минимальную ДНФ любым удобным вам способом.
Теоретические результаты, изложенные в этом параграФе, имеют важное значение при разработке элементной базы вычислительных машин.
Определение 24. Система булевых
функций у1 , Ь, ![]() зывается полной, если произвольная булева
функция может быть выражена через функции Л, „$2 ,
зывается полной, если произвольная булева
функция может быть выражена через функции Л, „$2 ,![]()
Пример 23. Полной является система функций &, v}. Действительно, согласно теоремам 1 и 2 (см. S 3.7), любая булева функция представима в виде СДНФ либо СКНФ, в выражении каждой из которых используются только упомянутые в примере функции.
Полноту других систем можно доказать с помощью следующего утверждения.
Утверждение. Пусть система у1 , Ь , — полна и любая из функций Л, Ь, fn может быть выражена через функции Щ, ..., gm. Тогда система , . , gm} также полна.
Задание. Докажите, что система функций v} является полной.
Решение. Для доказательства
воспользуемся сформулированным выше утверждением. Действительно, пусть f1(X1) =
il, f2(X1, Х2) = Х 1 V Х2 , f3(X1, Х2) = .Х1 & .Х2, ![]() g1(X1) = i1, g2(X1,
Х2) = х 1 х,' х,г.
g1(X1) = i1, g2(X1,
Х2) = х 1 х,' х,г.
![]() Выразим функции Л, f2, f3 через Ч, Ю : f1(X1) = g1(X1), f2(X1, Х2) =
g2(X1, Х2), f3(xp х2) = х 1 & х2 —
Выразим функции Л, f2, f3 через Ч, Ю : f1(X1) = g1(X1), f2(X1, Х2) =
g2(X1, Х2), f3(xp х2) = х 1 & х2 —![]() 2 g1(x2))).
2 g1(x2))).
Для выражения конъюнкции через дизъюнкцию и отрицание
был использован один из законов де Моргана. Ис- ![]() пользуя второй из этих
законов, можно доказать полноту системы Ь, &}.
пользуя второй из этих
законов, можно доказать полноту системы Ь, &}.
![]() Таким образом, любая
(сколь угодно сложная) булева функция может быть выражена через две функции
Таким образом, любая
(сколь угодно сложная) булева функция может быть выражена через две функции ![]()
![]() е,
&} или ъ, v}.
е,
&} или ъ, v}.
Определение 25. Логическая
функция штрих Шеффера ![]() (другое название И-НЕ) обозначается х2 и
задается следующей таблицей истинности:
(другое название И-НЕ) обозначается х2 и
задается следующей таблицей истинности: ![]()
|
|
|
|
||||||||||||||||||||
|
|
||||||||||||||||||||||
Пример 24. Докажем, что функция штрих Шеффера является полной. Построим для нее СКНФ, т. е. выразим ее через конъюнкцию, дизъюнкцию и отрицание.
х1 х2 = х1 v х2 или .х1 .х2 = х2 (последняя формула
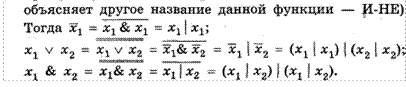
Таким образом, мы выразили через функцию штрих ШефФера функции &, v}. Следовательно, система, состоящая только из функции штрих Шеффера, полна.
Определение 26. Логическая функция стрелка Пирса (другое название ИЛИ-НЕ) обозначается х $ х и задается следующей таблицей истинности:
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
1 |
|
Можно доказать, что и система, состоящая из одной функции стрелка Пирса, является полной.
Вопросы и задания
1. Выразите функции &, м, через стрелку Пирса.
2. Докажите, что система функций, состоящая только из функции отрицания, не является полной.
З. Докажите, что система функций, состоящая только из функции конъюнкция, не является полной.
4. Докажите, что система функций {&, v} не является полной.
5. Используя второй закон де Моргана, докажите, что система Ь, &} полна.
6. Выразите функции & и v через и доказав тем самым полноту системы {—>, -4.
7. Как с помощью функции исключающее ИЛИ и одной из констант О или 1 (определите, какой именно) можно выразить логическое отрицание?
S З. 10. Элементы схемотехники. Логические схемы
Любое устройство компьютера, выполняющее арифметические или логические операции, может рассматриваться как преобразователь двоичной информации: значения входных переменных для него — последовательность нулей и единиц, а значения выходной функции — новая двоичная последовательность. Необходимые преобразования информации в блоках компьютера производятся логическими устройствами двух типов: комбинационными схемами и цифровыми автоматами с памятью.
В комбинационной схеме набор выходных сигналов в любой момент времени полностью определяется набором входных сигналов.
Определение 27. Дискретный преобразователь, который выдает
после обработки двоичных сигналов значение одной ![]() из логических
операций, называется логическим элементом (вентилем).
из логических
операций, называется логическим элементом (вентилем).
|
|
а |
1 |
а |
|
|
|
|
а
а б
Логический элемент И (конъюнктор) реализует операцию логического умножения (рис. 3.2, а). Единица на выходе этого элемента появится тогда и только тогда, когда на всех входах будут единицы.
Логический элемент ИЛИ (дизъюнктор ) реализует операцию логического сложения (рис. 3.2, б). Если хотя бы на одном входе будет единица, то на выходе элемента также будет единица, иначе на выходе будет ноль.
Логический элемент НЕ (инвертор) реализует операцию отрицания (рис. 3.2, в). Если на входе элемента ноль, то на выходе единица и наоборот.
![]()
1 Знак «1» на схеме элемента — дань устаревшему обозначению операции ИЛИ «21» — результат операции ИЛИ равен 1, если сумма значений операндов больше или равна 1.
Базовыми в микроэлектронике являются также логические элементы И-НЕ и ИЛИ-НЕ, реализующие функции штрих Шеффера и стрелка Пирса. Их условные обозначения:
|
|
|
1 |
|
Из отдельных логических элементов можно составить, например, устройства, производящие арифметические операции над двоичными числами.
Рассмотрим схему сложения двух п-разрядных двоичных чисел.
|
а |
ај |
...а Во |
|
|
Si |
...SISo |
При сложении цифр i-I'0 разряда складываются а. и Ь., к ним прибавляется ![]() признак переноса из (i
признак переноса из (i ![]() разряда. Результатом сложения будет
разряда. Результатом сложения будет ![]() — признак переноса в следующий
разряд.
— признак переноса в следующий
разряд.
Таким образом, одноразрядный двоичный сумма-
тор — это устройство с тремя входами и двумя выходами. Его работа описывается следующей таблицей истинНОСТИ:
|
|
Входы |
|
Выходы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
1 |
|
1 |
|
|
|
1 |
1 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
1 |
|
1 |
1 |
|
|
1 |
|
1 |
1 |
1 |
1 |
1 |
Выходные функции можно восстановить по таблице в виде СДНФ или СКНФ и упростить с помощью тождественных преобразований. В результате преобразований искомые функции приобретают, например, следующий вид:
![]()
Первое из соотношений (3.3) является решением задания 5, п. 1 к S 3.7. Второе из соотношений (3.3) выведено из СДНФ с учетом уже имеющегося выражения для 2+1.
Заметим, что функции pt+1 и .st можно выразить другими формулами, что, естественно, приведет к другим логическим схемам. Так, наиболее короткой формулой для s. является следующая: si i
![]()
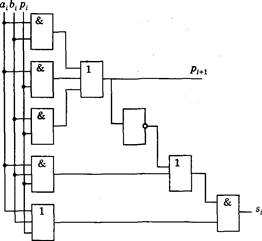
![]() Сложение п-разрядных
двоичных чисел осуществляется с помощью комбинации одноразрядных сумматоров
(условное обозначение одноразрядного сумматора приведено на рисунке слева.) В
зависимости от способа ввода/вывода данных и организации переносов
многоразрядные сумматоры бывают последовательного и параллельного принципа
действия.
Сложение п-разрядных
двоичных чисел осуществляется с помощью комбинации одноразрядных сумматоров
(условное обозначение одноразрядного сумматора приведено на рисунке слева.) В
зависимости от способа ввода/вывода данных и организации переносов
многоразрядные сумматоры бывают последовательного и параллельного принципа
действия.
В цифровых автоматах с памятью набор выходных сигналов зависит не только от набора входных сигналов, но и от внутреннего состояния данного устройства. Такие устройства всегда имеют память.
Определение 29. Логический элемент, способный хранить один разряд двоичного числа, называют триггером.
Триггер был изобретен в 1918 г. М. А. Бонч-Бруевичем (1888—1940). Самый простой триггер — RS. Он состоит из двух элементов ИЛИ-НЕ, входы и выходы которых соединены кольцом: выход первого соединен со входом второго, выход второго — со входом первого. Схема њ-триггера:
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Принцип работы њ-триггера иллюстрирует следующая таблица истинности:
|
Режимы работы триггера |
Входы
|
Состояние триггера |
|
|
Хранение предыдущего состояния |
о |
о |
|
|
Установка триггера в 1 |
|
1 |
1 |
|
Установка триггера в 0 |
1 |
|
|
|
Запрещенное состояние |
1 |
1 |
Недопустимо |
Обычно на входы поступают сигналы R = О и S = О, и триггер хранит старое состояние. Если на вход S поступает на короткое время сигнал 1, то триггер переходит в состояние 1, и после того, как сигнал S станет равен О, триггер будет сохранять состояние 1. При подаче 1 на вход R триггер перейдет в состояние О. Подача на оба входа логической единицы может привести к неоднозначному результату, поэтому такая комбинация входных сигналов запрещена.
Для хранения 1 байта информации необходимо 8 триггеров, для 1 килобайта — 8 х 1024 триггера. Таким образом, оперативная память современных компьютеров содержит миллионы триггеров. В целом же компьютер состоит из огромного числа логических элементов, образующих все его узлы и память.
Вопросы и задания
1. Проанализируйте схему, приведенную на следующем рисунке, и выпишите формулу для функции Р.
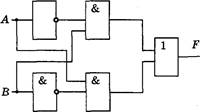
2.
З. Может ли произвольная логическая схема быть построена только из логических элементов одного типа?
4. Постройте схему трехразрядного сумматора из одноразрядных.
Заключение
Итак, подведем итоги. XIX век подарил
нам плеяду вы![]() дающихся математиков, которым удалось
построить стройный аппарат алгебры логики. В первую очередь это Джордж Буль,
Огастес де Морган, Джордж Венн.
дающихся математиков, которым удалось
построить стройный аппарат алгебры логики. В первую очередь это Джордж Буль,
Огастес де Морган, Джордж Венн.
Стремительный ХХ век расширил границы
практиче![]() ского применения теоретических
результатов алгебры логики. В частности, ее математический аппарат широко
используется в информатике, при проектировании компьютеров, в теории
алгоритмов, в целочисленном программировании и т. д.
ского применения теоретических
результатов алгебры логики. В частности, ее математический аппарат широко
используется в информатике, при проектировании компьютеров, в теории
алгоритмов, в целочисленном программировании и т. д.
Надеемся, что мы заинтересовали вас алгеброй логики — чрезвычайно красивой областью математики, применение которой будет наверняка расширяться.
Глава 4
![]()
Элементы теории алгоритмов
Понятие алгоритма является не только центральным понятием теории алгоритмов, не только одним из главных понятий математики вообще, но одним из главных понятий современной науки. Более того, сегодня, с наступлением эры информатики, алгоритмы становятся одним из важнейших факторов цивилизации.
В. А. Успенский
Благо везде и всюду зависит от соблюдения двух условий: 1) правильного установления цели всякого рода деятельности и 2) отыскания соответствующих средств, ведущих к этой цели.
Аристотель
S 4.1. Понятие алгоритма. Свойства алгоритмов
S 4.2. Уточнение понятия алгоритма. Машина Тьюринга
S 4.3. Машина Поста как уточнение понятия алгоритма
S 4.4. Алгоритмически неразрешимые задачи и вычислимые функции
S 4.5. Понятие сложности алгоритма
S 4.6. Анализ алгоритмов поиска
S 4.7. Анализ алгоритмов сортировки
![]()
анная глава знакомит вас с относительно новой научной дисциплиной — теорией алгоритмов. Заметим сразу, что специалист в области теории алгоритмов — это прежде всего математик, уверенно владеющий аппаратом теории множеств, дискретной математики, высшей алгебры. Зарождение и развитие теории алгоритмов связано с фундаментальными достижениями выдающихся математиков: А. Тьюринга (Англия), А. Чёрча (США), Э. Поста (США), Дж. фон Неймана (США), А. А. Маркова (СССР), П. С. Новикова (СССР), А. Н. Колмогорова (СССР), Г. С. Цейтина (СССР), Ю. В. Ма тиясевича (СССР) и многих других.
Глава посвящена разъяснению одного из
основных ![]() понятий математики и информатики понятия
алгоритма; в ней прослеживается взаимовлияние научных открытий математики и
информатики в области теории алгоритмов.
понятий математики и информатики понятия
алгоритма; в ней прослеживается взаимовлияние научных открытий математики и
информатики в области теории алгоритмов.
S 4.1 . Понятие алгоритма. Свойства алгоритмов
Каждый из нас ежедневно решает задачи различной сложности: как быстрее добраться в школу или на работу в условиях нехватки времени; в каком порядке выполнять дела, намеченные на текущий день, и т. д. Некоторые задачи настолько сложны, что требуют длительных размышлений для нахождения решения (иногда решение так и не удается найти), другие задачи мы решаем автоматически, так как выполняем их ежедневно на протяжении многих лет (выключить звенящий будильник; почистить утром зубы; позвонить другу по телефону). В большинстве случаев решение каждой задачи можно подразделить на простые этапы.
Пример 1. Задача «Звонок другу по телефону» подразделяется на следующие этапы (шаги):
1. Поднять телефонную трубку.
2. Если услышал гудок, то набрать номер друга, иначе конец решения задачи с отрицательным результатом (телефон неисправен).
З. Определить тип гудков: «вызов» или «занято». Если «вызов», перейти к шагу 4, если «занято», перейти к шагу 6.
4. Дождаться восьми вызывающих гудков.
![]()
5. Если за это время абонент не поднял трубку, то конец решения задачи с отрицательным результатом (абонент не отвечает), иначе начать разговор. Задача «Позвонить другу» решена успешно.
6. Положить телефонную трубку; конец решения задачи с отрицательным результатом (абонент занят). 2
Последовательность шагов, приведенная в примере 1, является алгоритмом решения задачи «Звонок другу по телефону». Исполнитель этого алгоритма человек. Объекты алгоритма — телефон и телефонные сигналы.
Для решения любой задачи надо знать, что дано и что следует получить, т. е. у задачи есть исходные данные (некие объекты) и искомые результаты. Для получения результатов необходимо знать способ решения задачи, т. е. располагать алгоритмом. В базовом курсе информатики вы знакомились с основами теории алгоритмов, в частности, вы знаете следующее неформальное определение (понятие) алгоритма.
Определение 1. Алгоритм это точная конечная система предписаний, определяющая содержание и порядок действий исполнителя над некоторыми объектами (исходными и промежуточными данными) для получения (после конечного числа шагов) искомого результата.

Аль-Хорезми
(780-850 н. э.) ![]() узбекский математик IX века; из
европеизированного произношения имени аль-Хорезми возник термин «алгоритм»
узбекский математик IX века; из
европеизированного произношения имени аль-Хорезми возник термин «алгоритм»
Приведенное определение не является определением в математическом смысле слова, это описание понятия алгоритма, раскрывающее его СУЩность. Оно не является формальным потому, что в нем используются такие неуточняемые понятия, как «система предписаний», «действия исполнителя», «объект».
Понятие алгоритма, являющееся фундаментальным понятием математики и информатики, возникло задолго до появления вычислительных машин .
Первоначально под словом «алгоритм» понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обо-
значения любой последовательности действий, приводящей к решению поставленной задачи.
Приведем примеры двух алгоритмов, которые будут вам полезны на уроках математики.
Пример 2. Рассмотрим способ выписывания всех простых чисел в интервале от 1 до некоторого N. Этот способ носит название «Решето Эратосфена», по имени древнегреческого ученого, впервые предложившего данный алгоритм.
![]() Эратосфен (ок. 275—194 до н. э.) один
из самых разносторонних ученых античности. Особенно прославили Эратосфена труды
по астрономии, географии и математике, однако он успешно трудился и в области
филологии, поэзии, музыки и философии
Эратосфен (ок. 275—194 до н. э.) один
из самых разносторонних ученых античности. Особенно прославили Эратосфена труды
по астрономии, географии и математике, однако он успешно трудился и в области
филологии, поэзии, музыки и философии
В результате применения этого алгоритма незачеркнутыми останутся все простые числа, не превосходящие N, и только они. Докажите это самостоятельно.
Пример З. Дано вещественное число Р. Требуется вычислить его квадратный корень с заданной точностью, например с т знаками после запятой.
Правило вычисления квадратного корня «в столбик»
можно записать в следующем виде:
1. Запись числа Р разделить на группы Р. по 2 цифры влево и вправо от запятой {Р1Р2...Рк,Рк 1 ...Рп}. Заметим, что самая левая и самая правая группы (Р 1 и Р ) могут состоять из одной цифры. Группу Рп в этом случае дополнить до двух цифр, приписав О справа.
2, Подобрать такую цифру х, квадрат которой не превосходит Р 1. Записать х в качестве первой цифры результата (искомого числа). З. Вычислить r = Р 1 — х 2.
4. Если нерассмотренных групп в числе Р больше нет и r= О (т. е. мы вычислили корень точно), или если r * О, но точность вычисления нас устраивает (у искомого числа получено т знаков после запятой), конец алгоритма.
5. Если нерассмотренные группы есть, или точность вычисления нас не устраивает, то к r дописать справа цифры очередной (РД группы; получившееся число обозначить через Ь. При этом возможны следующие варианты:
5.1) если очередная группа (Р.) стоит в записи числа первой после запятой, то ДОГмСм'Ь справа от х десятичную запятую;
5.2) если все группы в записи числа уже обработаны, то в качестве очередной группы Р. взять «00», при этом если число Р было целым, то дописать справа от х десятичную запятую.
6.
7. Вычислить — (2 • х'• 10 + у) • у.
8. Приписать у справа к результату. Получившееся число обозначить через х.
9. Перейти к шагу 4.
![]() Любой алгоритм существует не сам по себе, а предназначен
для определенного исполнителя. Алгоритм описывается в команДах исполнителя,
который этот алгоритм будет выполнять. Объекты, над которыми исполнитель может
совершать действия, образуют так называемую среду исполнителя. Исходные данные
и результаты любого алгоритма всегда принадлежат среде того исполнителя, для
которого предназначен алгоритм.
Любой алгоритм существует не сам по себе, а предназначен
для определенного исполнителя. Алгоритм описывается в команДах исполнителя,
который этот алгоритм будет выполнять. Объекты, над которыми исполнитель может
совершать действия, образуют так называемую среду исполнителя. Исходные данные
и результаты любого алгоритма всегда принадлежат среде того исполнителя, для
которого предназначен алгоритм.
Значение слова «алгоритм» очень схоже со значением слов «рецепт», «метод», «способ». Однако любой алгоритм, в отличие от рецепта или способа, обязательно обладает следующими свойствами,
1. Дискретность. Выполнение алгоритма разбивается на последовательность законченных действий-шагов. Только выполнив одно действие, можно приступать к исполнению следующего. Произвести каждое отдельное действие исполнителю предписывает специальное указание в записи алгоритма, называемое команДой.
2. Детерминированность. Способ решения задачи однозначно определен в виде последовательности шагов, т. е. если алгоритм многократно применяется к одному и тому же набору исходных данных, то каждый раз получаются одни и те же промежуточные результаты и один и тот же выходной результат.
З. Понятность. Алгоритм не должен
содержать предписаний, смысл которых может восприниматься исполнителем
неоднозначно, т. е. запись алгоритма должна быть настолько четкой и полной,
чтобы у исполнителя не возникало потребности в принятии каких-либо
самостоятельных решений. ![]()
Рассмотрим известный пример «бытового» алгоритма — алгоритм перехода улицы: «Посмотри налево. Если машин нет, дойди до середины улицы. Если есть, подожди, пока они проедут и т. д.». Представьте себе ситуацию: машина слева есть, но она не едет — у нее меняют колесо. Если вы думаете, что исполнитель алгоритма должен ждать, то вы поняли этот алгоритм. Если же вы решили, что улицу переходить можно, считая алгоритм подправленным в виду непредвиденных (по вашему мнению!) обстоятельств, то вы не усвоили понятие алгоритма.
4. Результативность. Содержательная определенность результата каждого шага и алгоритма в целом. При точном исполнении команд алгоритма процесс должен прекратиться за конечное число шагов, и при этом должен быть получен ответ на вопрос задачи. В качестве одного из возможных ответов может быть и установление того факта, что задача решений не имеет.
Свойство результативности содержит в себе свойство конечности — завершение работы алгоритма за конечное число шагов.
5. Массовость. Алгоритм пригоден для решения любой задачи из некоторого класса задач, т. е. алгоритм правильно работает на некотором множестве исходных данных, которое называется областью применимости алгоритма.
Проиллюстрируем свойства алгоритма на примере алгоритма вычисления квадратного корня «в столбик» (пример З).
Вопрос. Возможна ли ситуация, что способ решения заДачи есть, но он не является алгоритмом?
Ответ. Не каждый способ, приводящий к решению задачи, является алгоритмом. Например, опишем следующий способ (метод) проведения перпендикуляра к прямой MN, проходящего через заданную точку А:
1. Отложить в обе стороны от точки А на прямой MN циркулем отрезки равной длины с концами В и С.
2. Увеличить раствор циркуля до радиуса, в полтора-два раза большего длины отрезков АВ и АС.
З. Провести указанным раствором циркуля дуги окружностей с центрами В и С так, чтобы они охватили точку А и образовали две точки пересечения друг с другом (D и Е).
4. Взять линейку, приложить ее к точкам D и Е и соединить их отрезком.
При правильном построении отрезок пройдет через точку А и будет искомым перпендикуляром.
Указанный способ рассчитан на
исполнителя-челове![]() ка. Применяя его, человек, разумеется,
построит иско
ка. Применяя его, человек, разумеется,
построит иско![]() мый перпендикуляр. Но тем не менее этот
способ алгоритмом не является. Прежде всего он не обладает свойством
детерминированности. Так, в пункте 1 требуется от исполнителя сделать выбор
отрезка произвольной длины (для построения точек В и С можно провести
окружность произвольного радиуса r с центром в точке А). В пункте 2 требуется
сделать выбор отрезка, в полтора-два раза большего длины отрезков АВ и АС. В
пункте З надо провести дуги, которые также однозначно не определены.
Человек-исполнитель, применяющий данный способ к одним •и тем же исходным
данным (прямой МУ и точке А) повторно, получит несовпадающие промежуточные
результаты. Это противоречит требованию детерминированности алгоритма.
мый перпендикуляр. Но тем не менее этот
способ алгоритмом не является. Прежде всего он не обладает свойством
детерминированности. Так, в пункте 1 требуется от исполнителя сделать выбор
отрезка произвольной длины (для построения точек В и С можно провести
окружность произвольного радиуса r с центром в точке А). В пункте 2 требуется
сделать выбор отрезка, в полтора-два раза большего длины отрезков АВ и АС. В
пункте З надо провести дуги, которые также однозначно не определены.
Человек-исполнитель, применяющий данный способ к одним •и тем же исходным
данным (прямой МУ и точке А) повторно, получит несовпадающие промежуточные
результаты. Это противоречит требованию детерминированности алгоритма.
Вопрос. Существуют ли задачи, которые человек, вообще говоря, умеет решать, не зная при этом алгоритм их решения?

Дадим уточненное понятие алгоритма,
которое опять же не является определением в математическом смысле слова, но
более формально описывает понятие ![]() алгоритма, раскрывающее его сущность.
алгоритма, раскрывающее его сущность.
Определение 2. Алгоритм — это конечная система правил, сформулированная на языке исполнителя, которая определяет последовательность перехода от допустимых исходных данных к конечному результату и которая обладает свойствами дискретности, детерминированности, результативности, конечности и массовости.
Ограничение на набор допустимых действий означает, что для любого исполнителя имеются задачи, которые нельзя решить с его помощью.
При изучении алгоритмов важно разделять два понясия: запись алгоритма и выполнение алгоритма. В учебно-научной литературе термин «алгоритм» используется как в первом, так и во втором значении. Для более четкого изложения мы будем конкретизировать употребление этого термина.
В заключение данного параграфа сделаем три важных замечания.
1)
Существует много разных способов для записи (описания) одного и
того же алгоритма: ![]() текстовая форма записи;
текстовая форма записи; ![]() запись в
виде блок-схемы;
запись в
виде блок-схемы; ![]() запись алгоритма на каком-либо
алгоритмическом языке;
запись алгоритма на каком-либо
алгоритмическом языке; ![]() представление алгоритма в виде машины
Тьюринга или машины Поста.
представление алгоритма в виде машины
Тьюринга или машины Поста.
Выбор способа записи алгоритма зависит от нескольких причин. Если для вас наиболее важна наглядность записи алгоритма, то разумно использовать блок-схему. Если алгоритм небольшой, то его можно записать в текстовой форме. При этом команды могут быть пронумерованы (пример 1) или записаны в виде сплошного текста (пример 2).
2)
Вне зависимости от выбранной формы записи элементарные шаги
алгоритма (команды) при укрупнении объединяются в алгоритмические конструкции:
послеДовательные, ветвящиеся, циклические, рекурсивные. В 1969 году Эдсгер В.
Дейкстра в статье «Структуры данных и алгоритмы» доказал, что для записи любого
алгоритма достаточно трех основных алгоритмических конструкций:
последовательных, ветвящихся, цикличе![]() ских.
ских.
Вопросы и задания
1. Почему кулинарный рецепт приготовления торта нельзя считать алгоритмом? Какими свойствами алгоритма не обладает кулинарный рецепт?
2. Составьте алгоритм сложения в столбик двух натуральных чисел. Предполагается, что операция сравнения двух натуральных чисел для человека является выполнимой.
З. Переформулируйте способ проведения перпендикуляра к прямой в заданной точке так, чтобы он стал алгоритмом .
4. Есть двое песочных часов: на З минуты и на 8 минут. Для приготовления эликсира бессмертия его надо варить ровно 7 минут. Как это сделать?
Придумайте систему команд исполнителя «Колдун» . Запишите последовательность команд этого исполнителя для приготовления эликсира.
5. Приведите примеры алгоритмов, использующих ветвящиеся алгоритмические конструкции.
6. Приведите примеры алгоритмов, использующих циклические алгоритмические конструкции.
7. Приведите примеры рекурсивных алгоритмов.
8, Составьте в виде блок-схемы алгоритм нахождения факториала числа N.
9. Докажите, что при помощи алгоритма «Решето Эратосфена» действительно можно найти все простые числа из указанного диапазона.
S 4.2. Уточнение понятия алгоритма. Машина Тьюринга
![]()
4.2.1. Необходимость уточнения понятия алгоритма
Постепенно математики подходили к постановке и решению все более сложных задач. Так, например, Г. Лейбниц в XVII веке пытался построить общий алгоритм решения любых математических задач. В ХХ веке эта идея приобрела более конкретную форму: построить алгоритм проверки правильности любой теоремы при любой системе аксиом. Построить такие алгоритмы не удавалось, и математики выдвинули предположение: а вдруг для того или иного класса задач в принципе невозможно построить алгоритм решения? Следовательно, если алгоритма не существует, то они ищут то, чего нет.
На основе этого предположения возникло понятие алгоритмически неразрешимой задачи — задачи, для которой невозможно построить процедуру решения. Но для того, чтобы прекратить поиски решения задачи, относительно которой выдвинуто предположение о ее алгоритмической неразрешимости, надо было научиться математически строго доказывать факт отсутствия соответствующего алгоритма. А это возможно только в том случае, если существует строгое определение алгоритма. Поэтому возникла проблема: построить формальное определение алгоритма, аналогичное известному интуитивному понятию.
Попытки выработать формальное
определение алгоритма привели в 20—30-х годах ХХ века к возникновению теории
алгоритмов. В первой половине ХХ века разные математики (А. Тьюринг, Э. Пост,
А. Н. Колмогоров, А. А. Марков и др.) предложили несколько подходов к
формальному определению алгоритма: нормаль![]() ный алгоритм Маркова,
машина Тьюринга, машина Поста и т. д. В дальнейшем было показано, что все эти
определения эквивалентны.
ный алгоритм Маркова,
машина Тьюринга, машина Поста и т. д. В дальнейшем было показано, что все эти
определения эквивалентны.
![]() Тьюринг
признан одним из основателей информатики и теории искусственного интеллекта,
его считают первым теоретиком современного программирования и, наконец, первым
в мире хакером. Между прочим, его «хакерская деятельность» внесла во время
второй мировой войны существенный вклад в победу союзных войск над германским
флотом, а один из коллег Тьюринга однажды сказал: «Я не берусь утверждать, что
мы А. Тьюринг выиграли войну благодаря Тьюрингу. Однако (1912-1954) без
него могли бы ее и проиграть» .
Тьюринг
признан одним из основателей информатики и теории искусственного интеллекта,
его считают первым теоретиком современного программирования и, наконец, первым
в мире хакером. Между прочим, его «хакерская деятельность» внесла во время
второй мировой войны существенный вклад в победу союзных войск над германским
флотом, а один из коллег Тьюринга однажды сказал: «Я не берусь утверждать, что
мы А. Тьюринг выиграли войну благодаря Тьюрингу. Однако (1912-1954) без
него могли бы ее и проиграть» .
У Алана Тьюринга целью создания такой абстрактной воображаемой машины было получение возможности доказательства существования или несуществования алгоритмов решения различных задач. Руководствуясь этой целью, Тьюринг искал как можно более простую, «бед-
ную» алгоритмическую схему, лишь бы она была универсальной .
Прежде чем мы начнем знакомиться с машиной Тьюринга, необходимо сделать два общих замечания относительно объектов, с которыми работают алгоритмы.
При этом мы исходим из того, что имеется набор из 11 различных символов {O, 1, 2, З, 4, 5, 6, 7, 8, 9, +}. Используемые символы будем называть буквами, а их набор — алфавитом. В общем случае буквами могут служить любые символы, требуется только, чтобы они были различны между собой и чтобы их число было конечным •
Определение З. Любая конечная последовательность букв из некоторого алфавита называется словом в этом алфавите. Количество букв в слове называется длиной слова. Слово, в котором нет букв, называется пустым словом. Оно часто изображается символом «Л» или «ар.
Так, алгоритм сложения двух целых чисел перерабатывает слово, которое состоит из двух слагаемых, разделенных символом «+» , в слово, изображающее сумму.
![]() Итак, объекты реального мира можно изображать словами в
различных алфавитах. Это позволяет считать, что объектами работы алгоритмов
могут быть только слова.
Итак, объекты реального мира можно изображать словами в
различных алфавитах. Это позволяет считать, что объектами работы алгоритмов
могут быть только слова.
Определение 4. Слово, к которому применяется алгоритм, называется входным словом; слово, получаемое в результате работы алгоритма, называется выходным. Совокупность слов, к которым применим алгоритм, называется областью применимости алгоритма.
К сожалению, нельзя доказать, что все возможные объекты можно описать словами, так как само понятие объекта не было формально (то есть строго) определено. Но можно проверить, что для любого наугад взятого алгоритма, работающего не над словами, его объекты можно выразить так, что они становятся словами, а суть алгоритма от этого не меняется.
![]()
![]()
Будем считать, что алгоритмы работают со словами, и мы формально описываем объекты-слова, над котоо рыми работают алгоритмы, в некотором алфавите.
4.2.2. Описание машины Тьюринга
Далее для уточнения понятия алгоритма следует формально описать действия над объектами-словами и порядок выполнения этих действий. В качестве такой формальной схемы мы и рассмотрим машину Тьюринга.
Вопрос. Что же представляет собой машина Тьюринга?
Ответ. Машина Тьюринга — это строгое математическое построение, математический аппарат (аналогичный, например, аппарату дифференциальных уравнений), созданный для решения определенных задач. Этот математический аппарат был назван «машиной» по той причине, что по описанию его составляющих частей и функционированию он похож на вычислительную машину. Принципиальное отличие машины Тьюринга от вычислительных машин состоит в том, что ее запоминающее устройство представляет собой бесконечную ленту: у реальных вычислительных машин запоминающее устройство может быть как угодно большим, но обязательно конечным. Машину Тьюринга нельзя реализовать именно из-за бесконечности ее ленты. В этом смысле она мощнее любой вычислительной машины.
В каждой машине Тьюринга есть две части:
![]()
1) неограниченная в обе стороны лента, разделенная на ячейки;
2) автомат (головка для считывания/записи, управляемая программой).
Входное слово размещается на ленте по одной букве в расположенных подряд ячейках. Слева и справа от входного слова находятся только пустые ячейки (в алфавит А всегда входит «пустая» буква ао — признак того, что ячейка пуста).
Автомат может двигаться вдоль ленты влево или вправо, читать содержимое ячеек и записывать в ячейки буквы. Ниже схематично нарисована машина Тьюринга, автомат которой обозревает первую ячейку с данными:
![]()
Автомат каждый раз «видит» только одну ячейку. В зависимости от того, какую букву а. он видит, а также в зависимости от своего состояния q., автомат может выполнять следующие действия:
записать новую букву в обозреваемую ячейку; выполнить сдвиг по ленте на одну ячейку вправо/влево или остаться на месте; перейти в новое состояние.
То есть у машины Тьюринга есть три вида команд. Каждый раз для очередной пары (ф, а) машина Тьюринга может выполнить определенную команду в соответствии с программой.
Программа для машины Тьюринга представляет собой таблицу, в каждой клетке которой записана команда.
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Клетка (ф, а) определяется двумя параметрами — символом алфавита и состоянием машины. Команда представляет собой указание: какой символ записать в текущую ячейку, куда передвинуть головку чтения/записи, в какое состояние перейти машине. Для обозначения направления движения автомата используем одну из трех букв: «Л» (влево), «П» (вправо) или «Н» (неподвижен).
После выполнения автоматом очередной
команды он переходит в состояние qm (которое может в частном случае совпадать с
прежним состоянием Щ). Следующую команду нужно искать в т-й строке таблицы на
пересечении со ![]() столбцом at (букву at автомат видит после сдвига).
столбцом at (букву at автомат видит после сдвига).
Если следить только за лентой, не обращая внимания на автомат, то мы увидим, что в результате выполнения каждой команды изменяются слова: какие-то буквы стираются и вместо них остаются пустые ячейки, в каких-то ячейках появляются новые буквы.
Договоримся, что когда лента содержит входное слово, то автомат находится против какой-то ячейки в со-
стоянии Ъ. В процессе работы автомат будет перескакивать из одной клетки программы (таблицы) в другую, пока не дойдет до клетки, в которой записано, что автомат должен перейти в состояние qo. Эта клетка называется клеткой останова. Дойдя до любой такой клетки, машина Тьюринга останавливается.
![]() Если клеток останова в программе нет или машина в процессе
работы на них не попадает, то считается, что машина Тьюринга неприменима к
данному входному слову. Машина Тьюринга применима к входному слову только в том
случае, если, начав работу над этим входным словом, она рано или поздно дойдет
до одной из клеток останова.
Если клеток останова в программе нет или машина в процессе
работы на них не попадает, то считается, что машина Тьюринга неприменима к
данному входному слову. Машина Тьюринга применима к входному слову только в том
случае, если, начав работу над этим входным словом, она рано или поздно дойдет
до одной из клеток останова.
Вопрос. Прослеживая работу машины Тьюринга, мы можем только узнать, что она к Данному слову применима. Но если она к Данному слову неприменима, то такое прослеживание ничего не Даст, так как 6 любой момент времени мы можем надеяться Дойти до клетки останова. Как же выйти из этой ситуации?
|
|
|
|
1 |
|
|
|
оп |
|
Тогда, что бы автомат ни увидел на ленте, он ничего не меняет и сдвигается на шаг вправо, оставаясь всегда в состоянии Ь . А поскольку лента бесконечна, он никогда не остановится.
4.2.3. Примеры машин Тьюринга
Несмотря на свое простое устройство, машина Тьюринга может выполнять все возможные преобразования слов, реализуя тем самым все возможные алгоритмы.
Задание 1. Требуется построить машину
Тьюринга, кото![]() рая прибавляет еДиницу к числу на ленте.
Входное слово состоит из цифр целого Десятичного числа, записанных в
последовательные ячейки на ленте. В начальныЙ момент машина находится против
самой правой цифры числа.
рая прибавляет еДиницу к числу на ленте.
Входное слово состоит из цифр целого Десятичного числа, записанных в
последовательные ячейки на ленте. В начальныЙ момент машина находится против
самой правой цифры числа.
Решение. Машина должна прибавить единицу к последней цифре числа. Если последняя цифра равна 9, то ее надо заменить на О и прибавить единицу к предыдущей цифре. Программа для данной машины Тьюринга может выглядеть так:
|
|
|
Для краткости и наглядности записи программы машины Тьюринга можно условиться переход в состояние останова отмечать знаком «!» . Тогда программа из задания 1 будет выглядеть так:
|
|
|
о |
1 |
2 |
з |
4 |
|
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
Задание 2. Построить машину Тьюринга для подсчета штрихов, которые располагаются поДряД и образуют входное слово, при этом требуется стереть все штри-
хи и записать на ленте их количество в Десятичной системе.
Решение. Будем формировать искомое число на ленте слева от штрихов (без пустого символа между числом и штрихами). В начальный момент машина Тьюринга обозревает любой из штрихов и находится в состоянии Ъ.
Запишем алгоритм решения задачи в текстовой форме.
1. Найти правый конец слова на ленте.
2. Если слово оканчивается штрихом, то стереть этот штрих, иначе остановить машину.
З. Прибавить к числу единицу и перейти к п. 1.
В соответствии с этим алгоритмом каждый момент времени на ленте находится слово вида
![]()
Здесь bhbk 1...b1bo десятичная запись числа стертых штрихов, сразу после этой записи находятся еще не стертые штрихи.
![]() состояние q1
состояние q1 ![]() автомат ищет правый
конец слова;
автомат ищет правый
конец слова; ![]() состояние q2
состояние q2 ![]() автомат стирает
штрих;
автомат стирает
штрих; ![]() состояние
состояние![]() автомат ищет правый
конец числа и прибавляет к числу единицу.
автомат ищет правый
конец числа и прибавляет к числу единицу.
Ниже приведена программа машины Тьюринга для решения предлагаемой задачи.
|
|
|
о
|
1 |
2
|
з
|
|
8
|
9
|
|
|
|
00 Л п ч Ни |
они |
1 II q1 1 ни |
2 н % |
з н % |
|
|
|
|
|
|
1 Пи |
1 Пи |
З Пи |
4 IIq1 |
|
|
|
|
|
Проанализировав программы машин Тьюринга из заданий 1 и 2, можно сделать вывод, что программа машины Тьюринга для решения сложной задачи может состо-
![]()
ять из композиций (объединений) программ машин Тьюринга для решения элементарных подзадач исходного алгоритма. Таким же методом выделения в исходной задаче подзадач мы пользуемся при составлении алгоритмов в привычной для нас алгоритмической схеме (запись алгоритма в виде блок-схемы, в текстовом виде
Богатство возможностей машины Тьюринга проявляется в том, что если какие-то алгоритмы А и В реализуются машинами Тьюринга, то можно построить машины Тьюринга, реализующие различные композиции алгоритмов А и В. Например, «Выполнить А, затем выполнить В» или «Выполнить А. Если в результате получилось слово «да», выполнить В. В противном случае не выполнять В» или «Выполнять поочередно А, В, пока В не даст ответ О».
Очевидно, что такие композиции также являются алгоритмами, поэтому их реализация посредством машины Тьюринга подтверждает, что конструкция Тьюринга является универсальным исполнителем.
Математическое описание машины Тьюринга
Описывая различные алгоритмы для машины Тьюринга и доказывая реализуемость всевозможных композиций алгоритмов, Тьюринг убедительно показал разнообразие возможностей предложенной им конструкции, что позволило ему выступить со следующим тезисом.
Тезис Тьюринга. Всякий алгоритм может быть реализован соответствующей машиной Тьюринга.
В тезисе Тьюринга речь идет, с одной стороны, о понятии алгоритма, которое не является точным математическим понятием, с другой стороны, о точном матемаТИЧеСКОм ПОНЯТИИ — машине Тьюринга. Настало время показать, что машина Тьюринга — математическое понятие, т. е. она может получить точное математическое определение.
Определение 5. Машиной Тьюринга (МТ) называется система вида {А, ао, Q, Ъ, qo, Т, т}, где А — конечное множество, называемое алфавитом МТ,
![]() Е А — пустая буква алфавита,
Е А — пустая буква алфавита,
Q конечное множество, элементы которого
![]() называются
состояниями МТ,
называются
состояниями МТ,
![]() Е Q — начальное состояние МТ,
Е Q — начальное состояние МТ,
![]() Е Q — пассивное
состояние, или состояние останова МТ,
Е Q — пассивное
состояние, или состояние останова МТ,
![]() {Л, Н, П} — множество сдвигов МТ,
{Л, Н, П} — множество сдвигов МТ, ![]() программа
МТ, т. е. т: А х
программа
МТ, т. е. т: А х ![]() А х Т х Q.
А х Т х Q.
Нетрудно убедиться, что в этом определении фигурируют только математические и логические термины (или символы), например множество, конечное множество, элемент множества, принадлежность множеству, произведение множеств. И никакие другие, нематематические или нелогические понятия в приведенной формулировке не используются.
Тезис Тьюринга является основной гипотезой теории алгоритмов в форме Тьюринга. Одновременно этот тезис приводит к формальному определению алгоритма.
Определение 6. Алгоритм (по Тьюрингу) — программа для машины Тьюринга, приводящая к решению поставленной задачи.
![]() Основную гипотезу теории алгоритмов невозможно доказать,
потому что она оперирует неформальным понятием алгоритма. Однако обоснование
гипотезы есть: все алгоритмы, придуманные человечеством в течение столетий,
действительно могут быть реализованы машинами Тьюринга.
Основную гипотезу теории алгоритмов невозможно доказать,
потому что она оперирует неформальным понятием алгоритма. Однако обоснование
гипотезы есть: все алгоритмы, придуманные человечеством в течение столетий,
действительно могут быть реализованы машинами Тьюринга.
Чтобы опровергнуть основную гипотезу, необходимо придумать такой алгоритм, который невозможно было бы реализовать на машине Тьюринга. Пока такого алгоритма нет.
Выше мы с вами говорили, что каждый алгоритм предназначен для какого-то конкретного исполнителя, у каждого исполнителя есть своя система команд, есть свой круг задач. Тьюрингом же был построен универсальный исполнитель, который может решить любую известную задачу. Этот фундаментальный результат был получен в то время, когда универсальных вычислительных машин еще не существовало. Более того, сам факт построения воображаемого универсального исполнителя позволил высказать предположение о целесообразности построения универсальной вычислительной машины, которая бы могла решать любые задачи при условии соответствующего кодирования исходных данных и разработки соответствующей программы действий исполнителя.
![]() Тезис Тьюринга всегда
будет нацелен в будущее, так как теперь можно доказывать существование или
несуществование алгоритмов для решения любых возникающих задач. Если поиск
алгоритмического решения наталкивается на препятствие, то математики пытаются
использовать это препятствие для доказательства невозможности решения, опираясь
на основную гипотезу теории алгоритмов.
Тезис Тьюринга всегда
будет нацелен в будущее, так как теперь можно доказывать существование или
несуществование алгоритмов для решения любых возникающих задач. Если поиск
алгоритмического решения наталкивается на препятствие, то математики пытаются
использовать это препятствие для доказательства невозможности решения, опираясь
на основную гипотезу теории алгоритмов.
Вопросы и задания
1. Докажите, что любой алфавит можно заменить двухбуквенным алфавитом.
2.
З. Запишите программу машины Тьюринга из задания 2 с использованием знака «!» для обозначения перехода в состояние останова.
4. Постройте машину Тьюринга для решения
следующей задачи: во входном слове все буквы «а» заменить на бук![]() вы «б».
вы «б».
S 4,3. Машина Поста как уточнение понятия
алгоритма
Почти одновременно с Тьюрингом американский математик Эмиль Пост в 1937 году предложил иную абстрактную машину, характеризующуюся еще большей простотой, чем машина Тьюринга. Это строгое математическое построение было также предложено в качестве уточнения понятия алгоритма.
Определение 7. Алгоритм (по Посту) — программа для машины Поста, приводящая к решению поставленной задачи.
Американский математик и логик. Им получен ряд фундаментальных результатов в математической логике; он одним из первых ввел формальное определение алгоритма в терминах «абстрактной вычислительной машины»; кроме того, первым (одновременно с А. А. Марковым) привел доказательства алгоритмической неразрешимости ряда проблем математической логики и алгебры и сформулиэ. пост ровал основной тезис теории алгоритмов о (1897-1954) возможности описать любой конкретный алгоритм посредством этого определения.
Тезис Поста. Всякий алгоритм представим в форме машины Поста.
Этот тезис
одновременно является формальным опреде![]() лением алгоритма.
лением алгоритма.
Тезис Поста является гипотезой. Его невозможно строго доказать (так же, как и тезис Тьюринга), потому что в нем фигурирует, с одной стороны, интуитивное понятие «всякий алгоритм», а с другой стороны — точное понятие «машина Поста». В теории алгоритмов доказано, что машина Поста и машина Тьюринга эквивалентны по своим возможностям.
Вопрос. Что представляет собой машина Поста?
Ответ. В машине Поста в ячейках бесконечной ленты можно записывать всего два знака: 0 и 1 (ставить метку в ячейку или стирать метку). Это ограничение не влияет на ее универсальность, так как любой алфавит может быть закодирован двумя знаками.
Кроме ленты в машине Поста имеется каретка (головка чтения/записи), которая:
![]() умеет двигаться вперед, назад и стоять
на месте;
умеет двигаться вперед, назад и стоять
на месте;
• умеет читать содержимое, стирать и записывать 0 или 1; ![]() управляется
программой.
управляется
программой.
Как и машина Тьюринга, машина Поста может находиться в различных состояниях, но каждому состоянию соответствует не строка состояния с клетками, а некоторая команда одного из следующих шести типов (в синтаксисе команд указывается номер строки, поэтому все строки в программе пронумерованы):
1. Записать 1 (отметку), перейти к Г-й строке программы.
2. Записать 0 (стереть отметку), перейти к Г-й строке программы.
З. Выполнить сдвиг влево, перейти к ј-й строке программы.
4. Выполнить сдвиг вправо, перейти к Кй строке программы.
5. Останов.
6. Если О, то перейти к i-ff строке программы, иначе перейти к ј-й строке программы.
Состояние машины — это состояние ленты и положение каретки. Приведем список недопустимых действий, ведущих к аварийной остановке машины:
![]() попытка записать 1 (отметку) в
заполненную ячейку;
попытка записать 1 (отметку) в
заполненную ячейку; ![]() попытка стереть отметку в пустоЙ ячейке;
попытка стереть отметку в пустоЙ ячейке;
![]() е
уход каретки в бесконечность (вообще говоря, это трудно назвать остановкой, но
бессмысленное повторение одних и тех же действий зацикливание
е
уход каретки в бесконечность (вообще говоря, это трудно назвать остановкой, но
бессмысленное повторение одних и тех же действий зацикливание ![]() ничуть не
лучше вышеперечисленного).
ничуть не
лучше вышеперечисленного).
Машина Поста, несмотря на внешнюю
простоту, мо![]() жет производить различные вычисления, для
чего надо задать начальное состояние каретки и программу, которая эти
вычисления сделает. Условимся каждую строку программы обозначать номером. В
каждой строке программы записывается ровно одна команда. Команды машины будем
обозначать следующим образом:
жет производить различные вычисления, для
чего надо задать начальное состояние каретки и программу, которая эти
вычисления сделает. Условимся каждую строку программы обозначать номером. В
каждой строке программы записывается ровно одна команда. Команды машины будем
обозначать следующим образом:
![]() — шаг вправо, перейти к строке с номером
а;
— шаг вправо, перейти к строке с номером
а;
![]() — шаг влево, перейти
к строке с номером а; V a — записать отметку, перейти к строке с номером а; Х а
— стереть отметку, перейти к строке с номером а;
— шаг влево, перейти
к строке с номером а; V a — записать отметку, перейти к строке с номером а; Х а
— стереть отметку, перейти к строке с номером а;
![]() — просмотреть
ячейку; если в ячейке находится О, то перейти к строке с номером а, иначе
— просмотреть
ячейку; если в ячейке находится О, то перейти к строке с номером а, иначе ![]() к
строке с номером Ь;
к
строке с номером Ь;
— останов.
Вопрос. Чем отличаются состояния 6 машине Тьюринга от состояний в машине Поста?
Ответ. В машине Тьюринга состояние определяет, что следует записать в обозреваемую ячейку для каждого определенного символа, задает характер движения головки и, наконец, указывает новое состояние машины.
В машине Поста состояние описывает местонахождение каретки и состояние ленты.
Пример 4. На ленте проставлена отметка в одной-единственной ячейке. Каретка стоит на некотором расстоянии слева от этой ячейки. Необходимо подвести каретку к ячейке, стереть отметку и остановить каретку слева от нее.
Программа для машины Поста:
Вопросы и задания
1. Начальное состояние: лента машины Поста пуста. Что будет находиться на ленте в результате работы следующей программы?
![]()
2. Известно, что на ленте машины Поста находится метка. Напишите программу, которая находит ее.
З. На ленте имеется массив из п отмеченных ячеек. Каретка обозревает крайнюю левую отметку. Справа от данного массива на расстоянии в т ячеек находится еще одна отметка. Составьте для машины Поста программу, придвигающую данный массив к данной ячейке.
4. На ленте расположены два массива разной длины. Каретка обозревает крайний элемент одного из них. Составьте программу для машины Поста, сравнивающую длины массивов и стирающую больший из них. Отдельно продумайте случай, когда длины массивов равны.
S 4.4. Алгоритмически неразрешимые задачи и вычислимые функции
В предыдущих параграфах было введено
понятие алго![]() ритмически неразрешимой задачи, да и наше
воображение допускает, что, наверное, существуют задачи, которые невозможно
решить. А что же представляют собой такие задачи? Приведем несколько примеров
алгоритмически неразрешимых задач.
ритмически неразрешимой задачи, да и наше
воображение допускает, что, наверное, существуют задачи, которые невозможно
решить. А что же представляют собой такие задачи? Приведем несколько примеров
алгоритмически неразрешимых задач.
Дано произвольное алгебраическое уравнение ![]() х ) = О,
где Р — многочлен с целыми коэффициентами (например, ах: + ьх2 + схз О).
Требуется выяснить, существует ли у данного уравнения решение в целых числах.
х ) = О,
где Р — многочлен с целыми коэффициентами (например, ах: + ьх2 + схз О).
Требуется выяснить, существует ли у данного уравнения решение в целых числах.
Иная формулировка: требуется выработать алгоритм, позволяющий для любого диофантова уравнения выяснить, имеет ли оно целочисленное решение.
![]() Его называют последним всесторонним
математиком и самым замечательным учителем математиков ХХ века. Вундеркиндом он
не был, а был типичным «классиком», т. е. Гильберт поочередно старался понять
каждую область математики на всю ее глубину и решить в ней те задачи, которые
его интересовали.
Его называют последним всесторонним
математиком и самым замечательным учителем математиков ХХ века. Вундеркиндом он
не был, а был типичным «классиком», т. е. Гильберт поочередно старался понять
каждую область математики на всю ее глубину и решить в ней те задачи, которые
его интересовали.
Д. Гильберт (1862-1943)
В 1970 г. советский математик Ю. В. Матиясевич доказал невозможность построения алгоритма для решения этой задачи.
Замечание. Если известно, что решение в целых числах есть, то алгоритм отыскания этого решения сущестзует.
![]() Матиясевич Юрий Владимирович
(р. 1947), воспитанник школы-интерната им. А. Н. Колмогорова.
Член-корреспондент РАН с 1997 г., специалист в области математической логики,
теории алгоритмов, дискретной математики. Ю. В. Матиясевич
Матиясевич Юрий Владимирович
(р. 1947), воспитанник школы-интерната им. А. Н. Колмогорова.
Член-корреспондент РАН с 1997 г., специалист в области математической логики,
теории алгоритмов, дискретной математики. Ю. В. Матиясевич
Пример 6. По описанию алгоритма А и аргументу х необходимо выяснить, остановится ли алгоритм А, если х является входным данным. Эта задача (ее называют проблемой останова) является алгоритмически неразрешимой. Докажем это.
1. Выполнить алгоритм В над А.
2. Если алгоритм В определил, что А на своем тексте остановится, то перейти к шагу 1, в противном случае к шагу З.
З. Конец алгоритма С.
Применим алгоритм С к самому себе, т. е. входными данными для него будет текст алгоритма С. Пусть алгоритм В определил, что алгоритм С остановится при анализе своего текста. Но тогда после выполнения п. 2 мы снова перейдем к п. 1, т. е. на самом деле С в этом случае «зацикливается». Пусть, наоборот, алгоритм В опре-
делил бесконечность алгоритма С. Но тогда после выполнения п. 2 мы перейдем к п. З и алгоритм С завершится. Таким образом, так называемая «проблема самоприменимости алгоритма» неразрешима. Значит, наше предположение о существовании алгоритма В, решающего нашу задачу, неверно.
![]() Важным практическим следствием доказанного факта является
невозможность создания универсального (пригодного для любой программы) алгоритма
отладки программы.
Важным практическим следствием доказанного факта является
невозможность создания универсального (пригодного для любой программы) алгоритма
отладки программы.
Однако для конкретных алгоритмов и
некоторых ![]() классов алгоритмов проблему останова
и/или отладки соответствующей программы решить можно. Так, для программы,
состоящей только из линейных конструкций, легко показать, что она всегда закончит
свою работу.
классов алгоритмов проблему останова
и/или отладки соответствующей программы решить можно. Так, для программы,
состоящей только из линейных конструкций, легко показать, что она всегда закончит
свою работу.
![]()
![]()
Как известно, в современной математике почти все математические теории строятся на аксиоматической основе. Суть соответствующего аксиоматического метода состоит в следующем: все предложения (теоремы) данной теории получаются посредством формально-логического вывода из нескольких предложений (аксиом), принимаемых в данной теории без доказательства. Ранее других была осуществлена аксиоматизация геометрии.
Пусть у нас есть посылка R и следствие S, записанные в виде
слов (формул) в некотором специальном алфавите, состоящем из букв, скобок,
знаков математических и логических операций и т. д. Процесс вывода ![]() следствия
S из посылки R может быть описан в виде
следствия
S из посылки R может быть описан в виде ![]() процесса формальных
преобразований слов; считаем, что система допустимых преобразований указана, т.
е. построено логическое исчисление.
процесса формальных
преобразований слов; считаем, что система допустимых преобразований указана, т.
е. построено логическое исчисление.
Проблему распознавания выводимости можно
сфор![]() мулировать следующим образом: Существует
ли для
мулировать следующим образом: Существует
ли для ![]() любых двух слов (формул) R и S
ДеДуктивная цепочка, веДущая от R к S? Решение понимается в смысле
существования алгоритма, дающего ответ на этот вопрос для любых слов R и S.
любых двух слов (формул) R и S
ДеДуктивная цепочка, веДущая от R к S? Решение понимается в смысле
существования алгоритма, дающего ответ на этот вопрос для любых слов R и S.
Несмотря на долгие и упорные усилия многих крупных специалистов, трудности, связанные с таким построением, оказались непреодолимыми. В рамках теории алгоритмов был получен отрицательный ответ на вопрос об алгоритмической разрешимости этой проблемы. В 1936 году американский математик Чёрч доказал следующую теорему.
Теорема Чёрча. Проблема распознавания выводимости алгоритмически неразрешима.
Вопрос. Какие методы используются для Доказательства алгоритмической неразрешимости?
Ответ. Обычно алгоритмическая неразрешимость новых задач доказывается метоДом сведения к этим задачам известных алгоритмически неразрешимых задач. Тем самым доказывается, что если бы была разрешима новая задача, то можно было бы решить и заведомо неразрешимую задачу. Применяя метод сведения, обычно ссылаются на искусственные задачи, которые не представляют самостоятельного интереса, но для которых легко непосредственно доказать их неразрешимость.
Но вернемся вновь к задачам, которые имеют алгоритмическое решение. В предыдущих параграфах мы показали, что если задача имеет решение, то можно написать и машину Тьюринга, и машину Поста для решения этой задачи. При этом на входные данные накладываются формальные ограничения (входные слова кодируются в некотором алфавите), а сами алгоритмы сконструированы в разных алгоритмических моделях (схемах). Возникает вопрос: можно ли в принципе говорить об общих свойствах алгоритмов при такой конкретизации?
В теории алгоритмов строго доказано, что любой алгоритм, описанный в одной модели, может быть описан и в другой. Такая взаимная сводимость алгоритмических моделей позволила создать систему понятий, не зависящую от выбора конкретной формализации понятия алгоритма. В основе этой системы лежит понятие вычислимой функции.
![]() Заметим, что
относительно каждого алгоритма А можно сказать, что он вычисляет значение
функции ЕА (реализует функцию FA) при некоторых значениях входных величин.
Заметим, что
относительно каждого алгоритма А можно сказать, что он вычисляет значение
функции ЕА (реализует функцию FA) при некоторых значениях входных величин.
Введенное понятие вычислимой функции, так же, как и понятие алгоритма, является интуитивным.
Фактически алгоритм это способ задания функции. Функции могут задаваться и другими способами, например таблицей или формулой. Однако существуют и такие задачи, в которых связь между входными и выходными параметрами настолько сложна, что нельзя составить алгоритм преобразования входных данных в результат. Такие функции являются не вычислимыми.
Пример 8 [4] , Рассмотрим функцию
![]() 1, если в десятичном разложении л есть отрезок из п
девяток, окруженный недевятками; О в противном случае.
1, если в десятичном разложении л есть отрезок из п
девяток, окруженный недевятками; О в противном случае.
Для каждого конкретного п можно подсчитать значение функции. Однако нам не известен общий способ, позволяющий вычислить значение функции для произвольного п. Анализ первых 800 знаков разложения тс показывает лишь, что h(n) = 1 для п = О, 1, 2, 6. Если не
существует общего правила вычисления этой функции, то не существует и алгоритма, реализующего эту функцию, т. е. решающего поставленную проблему.
Понятия алгоритма и вычислимой функции являются, пожалуй, наиболее фундаментальными понятиями информатики и математики. Систематическое изучение алгоритмов и различных моделей вычислений привело к созданию особой дисциплины, пограничной между математикой и информатикой — теории алгоритмов, в которой выделен раздел «теория вычислимости» ,
Вопросы и задания
1. Сравните определение функции из курса математики с определением вычислимой функции. Укажите общее и различное.
2. Приведите пример алгоритма, программная реализация которого затруднена.
З. Используя рассуждения примера 6, докажите, что невозможно создать универсальный (пригодный для любой программы) алгоритм отладки программы.
4. Приведите примеры универсальных исполнителей.
5. Выпишите хронологию фундаментальных достижений (с указанием фамилий авторов и дат их жизни) в области теории алгоритмов. Для каждого ученого вычислите, на каком году жизни он выполнил работу, приведшую к фундаментальным результатам в теории алгоритмов. Полученные результаты представьте в виде таблицы.
S 4.5. Понятие сложности алгоритма
В предыдущих параграфах говорилось, что если для решения задачи существует один алгоритм, то можно придумать и много других алгоритмов для решения этой же задачи.
Вопрос. Какой алгоритм лучше поДхоДит для решения конкретной задачи? По каким критериям следует выбирать алгоритм из множества возможных?
Более того, мы можем написать громоздкий алгоритм, в котором выписаны подряд повторяющиеся действия (без использования циклической структуры). Однако с точки зрения компьютерной реализации практически нет никакой разницы, использован ли в программе оператор цикла (например, 10 раз на экран выводится слово «Привет») или 10 раз последовательно выписаны операторы вывода на экран слова «Привет». Поэтому для оценки эффективности алгоритмов введено понятие сложности алгоритма.
Определение 9. Вычислительным процессом, порожденным алгоритмом, называется последовательность шагов алгоритма, пройденных при исполнении этого алгоритма.
В дальнейшем будем понимать под сложностью алгоритма количество элементарных действий в вычислительном процессе этого алгоритма, как функцию от исходных данных.
Обратите внимание, именно в вычислительном процессе, а не в самом алгоритме. Очевидно, для сравнения сложности разных алгоритмов необходимо, чтобы сложность подсчитывалась в одних и тех же элементарных действиях.
Определение 10. Временная сложность алгоритма это время Т, необходимое для его выполнения в зависимости от исходных данных. Оно равно произведению числа элементарных действий К на среднее время выполнения одного действия t: Т = kt.
Поскольку t зависит от исполнителя, реализующего алгоритм, то естественно считать, что сложность алгоритма в первую очередь определяется значением К. Очевидно, что в наибольшей степени количество операций при выполнении алгоритма зависит от количества обрабатываемых данных. Действительно, для упорядочивания по алфавиту списка из 100 фамилий требуется существенно меньше операций, чем для упорядочивания списка из 100 000 фамилий. Поэтому сложность алгоритма выражают в виде функции от объема входных данных.
Определение 11. Будем говорить, что
Т(п) алгоритма имеет порядок роста f(n), или алгоритм имеет теоретическую
сложность 0(f(n)) (читается «о большое от f(n)»), если для Т(п) найдется такая
константа с, что, начиная с неКОТОРОГО по, выполняется условие Т(п) cf(n).
Здесь предполагается, что функция f(n) неотрицательна, по крайней мере при п п ![]()
Так, например, алгоритм, выполняющий только операции чтения данных и занесения их в оперативную память, имеет линейную сложность Оф). Алгоритм сортировки методом прямого выбора, как это будет показано ниже, имеет квадратичную сложность 0(п 2 ), так как при сортировке любого массива этот алгоритм будет выполнять (п — п)/2 операций сравнения (при этом операций перестановок вообще может не быть, например, на упорядоченном массиве). А сложность алгоритма умножения матриц (таблиц) размера п х п будет уже кубической 00 3 ), так как для вычисления каждого элемента результирующей матрицы требуется п умножений и п — 1 сложений, а всего этих элементов п .
Для решения задачи могут быть разработаны алгоритмы различной сложности. Логично воспользоваться лучшим среди них, т. е. имеющим наименьшую сложность.
Наряду со сложностью важной
характеристикой алгоритма является эффективность. Под эффективностью понимается
выполнение следующего требования: не только весь алгоритм, но и каждый шаг его
должны быть такими, чтобы исполнитель был способен выпол![]() нить их за разумное
время. Например, если алгоритм, выдающий прогноз погоды на ближайшие сутки,
будет выполняться неделю, то такой алгоритм просто-напросто никому не нужен.
нить их за разумное
время. Например, если алгоритм, выдающий прогноз погоды на ближайшие сутки,
будет выполняться неделю, то такой алгоритм просто-напросто никому не нужен.
Известно, что во многих языках программирования нет операции возведения в степень (Р), следовательно, алгоритм возведения в целую степень программисту надо реализовывать самостоятельно. Операция возведения в степень выражается через операции умножения; с ростом показателя степени, естественно, растет количество операций умножения, которые при выполнении занимают достаточно долго время процессора. При реализации алгоритма возведения в степень «в лоб» надо выполнить (п — 1) операцию умножения. Существует ли более быстрый универсальный способ?
Метод быстрого вычисления натуральной степени п вещественного числа х
Этот метод был описан еще до нашей эры в Древней Индии.
1. Записать п в двоичной системе счисления.
2. Заменить в этой записи каждую 1 парой букв КХ, а каждый О буквой К.
З. Вычеркнуть крайнюю левую пару КХ.
4. Полученная строка, читаемая слева направо, дает правило быстрого вычисления х п , если букву К рассматривать как операцию возведения результата в квадрат, а букву Х — как операцию умножения результата на х. В начале результат равен х.
Пример 9. Возвести х в степень п = 100.
1. Перевести число п в двоичную систему счисления:
п = 10010 ![]() 11001002.
11001002. ![]()
2. Построить последовательность КХКХКККХКК. З. Вычеркнуть КХ слева КХКККХКК.
4. Вычислить искомое значение:
2
К: возвести х в квадрат х , з
![]() умножить
результат на х х
умножить
результат на х х ![]()
6
К: возвести результат в квадрат![]()
12
К:
возвести результат в квадрат х ![]()
24
25
![]() умножить результат на х х
умножить результат на х х ![]()
50
![]() К:
возвести результат в квадрат гэ х
К:
возвести результат в квадрат гэ х ![]()
100
К: возвести результат в квадрат гэ![]()
Таким образом, мы вычислили сотую степень числа х всего за 8 умножений. Этот метод достаточно эффективный, и он не требует дополнительной оперативной памяти для хранения промежуточных результатов. Однако заметим, что этот метод не всегда самый быстрый.
Сама операция умножения реализуется в процессоре не «в лоб», а через эффективные рекурсивные алгоритмы. Мы же рассмотрим алгоритм «быстрого» умножения, который был известен еще в Древнем Египте, его также называют «русским» или «крестьянским» методом, на конкретном примере.
Пример 10. Умножим 23 на 43 «русским» методом.
|
23 х 43 |
нечетное |
Первый столбец состоит из результатов последовательного умножения первого сомножителя (23) на 2. Второй столбец представляет собой результаты последовательного целочисленного деления второго сомножителя 43 на 2 |
|
46 21 |
нечетное |
|
|
92 10 |
|
|
|
184 5 |
(нечетное |
|
|
368 2 |
|
|
|
736 1 |
(нечетное) |
Результат равен сумме чисел первого столбца, рядом с которыми во втором столбце стоят нечетные числа. Ответ: 23 х 43 = 23 + 46 + 184 + 736 = 989.
Вопросы и задания
1. Подсчитайте сложность алгоритма перемножения двух натуральных чисел столбиком при условии, что одно из чисел состоит из п десятичных цифр, а второе — из т десятичных цифр.
2. Подсчитайте сложность алгоритма умножения двух натуральных чисел «русским» методом при условии, что одно из чисел состоит из п десятичных цифр, а второе — из т десятичных цифр.
З. Приведите примеры алгоритмов, имеющих линейную сложность.
![]()
S 4.6. Анализ алгоритмов поиска
В этом параграфе мы будем рассматривать
классические задачи поиска, анализировать алгоритмы, реализующие эти задачи, т.
е. изучать свойства алгоритмов. Из большого множества алгоритмов поиска мы
рассмотрим только два алгоритма, предназначенных для решения этой вос![]() требованной задачи.
требованной задачи.
Рассматривая различные алгоритмы решения одной и той же задачи, полезно проанализировать, сколько вычислительных ресурсов они требуют (время работы, память), и выбрать наиболее эффективный. Однако вначале надо договориться, какая модель вычислений будет использоваться. Будем считать, что наши алгоритмы выполняются на обычной однопроцессорной машине с произвольным доступом к памяти (данным).
В алгоритмах поиска существует две возможности окончания работы: либо поиск оказался удачным, т, е. позволил определить положение соответствующего элемента, либо он оказался неудачным, т. е. показал, что необходимого элемента в данном объеме информации нет.
Хотя целью поиска является значение элемента, алгоритмы поиска в случае удачного окончания выдают местоположение искомого элемента, например номер элемента в массиве.
В качестве критерия оценки алгоритма мы будем использовать такую характеристику, как сложность.
4.6.1 . Последовательный поиск в неупорядоченном массиве
Сформулируем алгоритм последовательного
поиска в не![]() упорядоченной последовательности
(неупорядоченном массиве). Очевидно, что этот алгоритм можно применять и для
поиска в упорядоченном массиве.
упорядоченной последовательности
(неупорядоченном массиве). Очевидно, что этот алгоритм можно применять и для
поиска в упорядоченном массиве.
Алгоритм последовательного поиска в неупорядоченном массиве
Имеется массив а[1..п], требуется найти элемент массива, равный Р.
1. Установить i — 1.
2. Если ај = Р, алгоритм окончен удачно.
З. Увеличить i на 1.
4. Если i п, то перейти к шагу 2. В противном случае алгоритм окончен неудачно.
![]() Сложность алгоритмов поиска естественно оценивать по числу
сравнений элементов массива с искомым элементом. В худшем случае (искомый
элемент Р стоит на последнем месте или отсутствует) сложность алгоритма будет
равна п.
Сложность алгоритмов поиска естественно оценивать по числу
сравнений элементов массива с искомым элементом. В худшем случае (искомый
элемент Р стоит на последнем месте или отсутствует) сложность алгоритма будет
равна п.
Усложним задачу. Пусть нам требуется
найтй минимальный элемент в неупорядоченном массиве. Оказывается, что этот
алгоритм также имеет линейную сложность, и для поиска минимального
(максимального) эле![]() мента в неупорядоченном массиве
потребуется п — 1 сравнений. Приведем этот алгоритм в текстовой форме и в виде
блок-схемы.
мента в неупорядоченном массиве
потребуется п — 1 сравнений. Приведем этот алгоритм в текстовой форме и в виде
блок-схемы.
![]() Алгоритм
поиска минимального элемента в неупорядоченном массиве
Алгоритм
поиска минимального элемента в неупорядоченном массиве
1. min = Ч.
2. Установить 1.
З. Если i < п, то перейти к шагу 4, иначе алгоритм окончен (минимальный элемент равен min).
4. Увеличить i на 1.
5. Если ај < min, то присвоить min значение щ.
6. Перейти к шагу З.
Еще более усложним задачу. Пусть нам требуется найти в неупорядоченном массиве максимальный и минимальный элементы одновременно. Можно скорректировать вышеприведенный алгоритм следующим образом:
1. min = Ч, тах = Ч.
2. Установить i 1.
4. Увеличить i на 1.
5. Если а. < min, то min присвоить значение а .
6. Если а. > тах, то тах присвоить значение а .
7. Перейти к шагу З.
Сложность этого алгоритма равна 2(n —
1). Зададимся вопросом, можно ли написать алгоритм с меньшей сложностью.
Оказывается, можно написать алгоритм, сложность которого будет равна З![]()
2
Эффективный алгоритм поиска в неупорядоченном массиве максимального и минимального элементов одновременно
1. Разбить массив на пары (получим пар, при нечетном п — плюс еще один элемент). 2
2. Упорядочить по возрастанию каждую пару (при выпол-
нении этого шага будет выполнено сравнений). Тогда
2
в массиве на всех нечетных местах будет стоять минимальное для данной пары число, а на всех четных местах максимальное .
З. Найти минимальное число, осуществляя поиск только среди элементов, стоящих на нечетных местах. При этом, если у нас есть неполная пара, то в качестве начального значения переменной min взять значение элемента неполной пары (при выполнении этого шага будет выполнено сравнений).
2
4. Найдем максимальное число, осуществляя поиск только среди элементов, стоящих на четных местах. При этом если у нас есть неполная пара, то в качестве начального значения переменной тах взять значение элемента неполной пары (при выполнении этого шага будет
выполнено сравнений). д
2
Всего сравнений в данном алгоритме З •![]()
4.6.2. Алгоритм бинарного поиска в упорядоченном
массиве
Пусть нам требуется найти элемент в
большом упорядоченном массиве информации, которая расположена в оперативной
памяти компьютера. Для решения этой задачи разработаны эффективные алгоритмы,
наиболее ![]() распространенным из них является алгоритм
бинарного (Дзоичного) поиска, его иногда называют логарифмическим поиском, или
методом Деления пополам (Дихотомией).
распространенным из них является алгоритм
бинарного (Дзоичного) поиска, его иногда называют логарифмическим поиском, или
методом Деления пополам (Дихотомией).
Основная идея бинарного поиска довольно проста, детали же нетривиальны, и правильно работающий алгоритм удается написать далеко не с первого раза. Одна из наиболее популярных реализаций этого алгоритма использует два указателя (Ь и и), соответствующие нижней и верхней границам поиска. С помощью этого алгоритма ищется элемент К в упорядоченном по возрастанию массиве а, содержащем п элементов.
Алгоритм бинарного поиска в упорядоченном массиве
1. Начальная установка: I = 1, и = п.
2. Если и < l, то алгоритм окончен неудачно. В противном случае найти середину интервала [l; и]. В этот момент мы знаем, что если К есть в массиве, то выполняются неравенства а! К аи. Установить i = [(l + и)/2]. Теперь i указывает примерно в середину рассматриваемой части массива.
З. Если К < at, то перейти к шагу 4, если К ::> щ, то перейти к шагу 5, если = ај, алгоритм окончен удачно.
4. Установить и = i — 1 и перейти к шагу 2.
5. Установить I = i + 1 и перейти к шагу 2.
![]() Шаг З алгоритма бинарного поиска выполняется порядка log2n
раз, т. е. данный алгоритм имеет логарифмическую сложность по числу сравнений.
Шаг З алгоритма бинарного поиска выполняется порядка log2n
раз, т. е. данный алгоритм имеет логарифмическую сложность по числу сравнений.
Вопросы и задания
1.
2. При реализации поиска в неупорядоченном массиве применяют следующий прием. Массив увеличивают на один элемент, присваивая этому элементу значение искомого элемента. Какой выигрыш при этом мы можем получить?
З. Для поиска элемента в упорядоченном массиве был применен алгоритм бинарного поиска. В худшем случае алгоритм 5 раз выполнял шаг З (осуществлял сравнения). Какое максимальное количество элементов может содержать такой массив?
4. Процедура двоичного поиска нашла искомый элемент в упорядоченном массиве за две итерации (шаг З выполнялся 2 раза). Сколько всего элементов может содержать массив, если наиденный элемент стоит в массиве на 23-м месте?
S 4.7. Анализ алгоритмов сортировки
Сортировка — один из наиболее
распространенных процессов современной обработки данных. Сортировкой на![]() зывается распределение элементов множества по группам в соответствии с
определенными правилами. Например, сортировка элементов массива, в результате
которой получается массив, каждый элемент которого, начиная со второго, не
больше стоящего от него слева, называется сортировкой по невозрастанию.
зывается распределение элементов множества по группам в соответствии с
определенными правилами. Например, сортировка элементов массива, в результате
которой получается массив, каждый элемент которого, начиная со второго, не
больше стоящего от него слева, называется сортировкой по невозрастанию. ![]()
В данной главе мы будем рассматривать только так называемые внутренние сортировки. Алгоритмы внутренней сортировки применяются для переупорядочивания данных, которые полностью располагаются в оперативной (внутренней) памяти. В этом случае мы имеем так называемый прямой (произвольный) Доступ к элементам массива. В отличие от внутренней сортировки, существуег внешняя сортировка, алгоритмы такой сортировки используют память на внешних носителях (например, сортировка данных с последовательным доступом, хранящихся в файлах на жестком диске).
Способов сортировки очень много, их можно разбить на группы в зависимости от идеи, лежащей в их основе.
Рассмотрим и проанализируем несколько
алгоритмов сортировки для решения следующей задачи. Дан одномерный массив целых
чисел. Требуется отсортировать его так, чтобы все элементы были расположены в
поряд![]() ке неубывания: a[i] a[i + 1], i = 1, 2,
ке неубывания: a[i] a[i + 1], i = 1, 2,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассматриваемый ниже алгоритм относится
к обменным сортировкам. Свое название «сортировка методом «пу![]() зырька» он
получил на основе следующей ассоциации: если мы будем сортировать этим
алгоритмом массив по
зырька» он
получил на основе следующей ассоциации: если мы будем сортировать этим
алгоритмом массив по ![]() убыванию, то минимальный элемент
«всплывает», а
убыванию, то минимальный элемент
«всплывает», а ![]() «тяжелые» элементы опускаются на одну
позицию к началу массива при каждом шаге алгоритма.
«тяжелые» элементы опускаются на одну
позицию к началу массива при каждом шаге алгоритма.
Алгоритм обменной сортировки методом «пузырька»
![]() Алгоритм начинается со сравнения 1-го и
2-го элементов
Алгоритм начинается со сравнения 1-го и
2-го элементов ![]() массива. Если элементы расположены не по
порядку, то они меняются местами. Этот процесс повторяется со 2-м и 3-м, 3-м и
4-м и т. д. элементами, пока пара ((п—1)-й и п-й элемент) не будет обработана.
За один просмотр массива самый большой элемент встанет на старшее (п-е) место.
Далее алгоритм повторяется, причем на р-м просмотре уже только первые (п — р)
элементов сравнивают
массива. Если элементы расположены не по
порядку, то они меняются местами. Этот процесс повторяется со 2-м и 3-м, 3-м и
4-м и т. д. элементами, пока пара ((п—1)-й и п-й элемент) не будет обработана.
За один просмотр массива самый большой элемент встанет на старшее (п-е) место.
Далее алгоритм повторяется, причем на р-м просмотре уже только первые (п — р)
элементов сравнивают![]() ся со своими правыми соседями. Если при
очередном просмотре перестановок не было или р = п, то алгоритм окончен. д
ся со своими правыми соседями. Если при
очередном просмотре перестановок не было или р = п, то алгоритм окончен. д
Для того чтобы оценить сложность этого алгоритма, мы должны подсчитать количество действий, выполняемых при сортировке массива размерностью п. При достаточно большом п мы можем пренебречь всеми действиями, кроме действий сравнения элементов между собой и перестановки двух элементов массива.
Договоримся обработку элементов неупорядоченной части массива во время одного просмотра называть итерацией алгоритма.
Подсчитаем количество операций сравнений и присваиваний (одна перестановка реализуется тремя операциями присваивания) для случая, когда на вход алгоритма подается уже отсортированный массив.
Пример 11. Дан массив {1 2 З 4 5}. К нему применен алгоритм сортировки «пузырьком». Сделано 4 сравнения, О перестановок. После первого же просмотра массива алгоритм закончил свою работу.
Пример 12. Дан массив {5 4 З 2 1}.
1-я итерация: {4 З 2 1 5} (4 сравнения, 4 перестановки).
2-я итерация: {З 2 1 4 5} (З сравнения, З перестановки).
3-я итерация: {2 1 З 4 5} (2 сравнения, 2 перестановки).
4-я итерация: {1 2 З 4 5} (1 сравнение, 1 перестановка). Алгоритм работу закончил. Было сделано 4 + З + 2 + 1 — = 10 сравнений и 10 перестановок.
В общем случае для обменной сортировки методом «пузырька» верны следующие оценки:
|
Количество с авнений |
Количество п исваиваний |
||
|
минимальное |
максимальное |
минимальное |
максимальное |
|
|
п—1+п—2+п—З+ |
|
3(п-1+п-2+п-3+ |
Алгоритм сортировки «пузырьком» имеет квадратичную сложность ).
Сортировка методом «пузырька» легко запоминается. Но этот метод сортировки на практике в том виде, как было рассказано, не используется. Этому есть несколько причин, в частности много раз приходится просматривать массив, и, как следствие, программа работает долго. На основе алгоритма сортировки методом «пузырька» можно построить много улучшенных модификаций, например, если на какой-либо итерации первые К пар не участвовали в обмене, то на следующей итерации просмотр можно начинать с (К + 2)-го элемента.
4.7.2. Сортировка выбором
Данная сортировка также относится к обменным. Приведем сначала алгоритм этой сортировки в текстовой форме.
![]()
Запишем этот алгоритм более подробно с разбивкой по шагам. При описании будем использовать следующие обозначения:
![]() а[1..п] исходный
массив;
а[1..п] исходный
массив; ![]() количество элементов в неупорядоченной
части массива.
количество элементов в неупорядоченной
части массива.
Алгоритм сортировки выбором
1. Положить r = п.
2. Найти наибольший элемент в массиве a[l..r]. Его место обозначим через тах.
З. Если тах -72 и а[тах] a[r], то поменять местами элементы а[тах] и a[r].
4. Передвинуть границы упорядоченной и неупорядоченной частей массива: r = r — 1. Первые r элементов будут образовывать неупорядоченную часть массива. Последние п — элементов — упорядоченную по возрастанию часть массива.
5. Если r 1, то алгоритм окончен, иначе перейти к шагу 2.
Для оценки сложности алгоритма
сортировки выбо![]() ром, как и для алгоритма сортировки
«пузырьком», подсчитаем количество операций сравнения и перестановою
ром, как и для алгоритма сортировки
«пузырьком», подсчитаем количество операций сравнения и перестановою
Пример 13. Вначале рассмотрим случай,
когда на вход алго![]() ритма подается уже отсортированный массив
{1 2 З 4 5}.
ритма подается уже отсортированный массив
{1 2 З 4 5}.
1-я итерация: 4 сравнения, О перестановок.
2-я итерация: З сравнения, О перестановок.
3-я итерация: 2 сравнения, О перестановок.
4-я итерация: 1 сравнение, О перестановок.![]()
Алгоритм окончен. Было сделано 4 + З + 2
+ 1 = 10 срав![]() нений и О перестановок.
нений и О перестановок.
Алгоритм окончен. Было сделано 4 + З + 2 + 1 = 10 сравнений и 2 перестановки.
![]() Максимальное
количество перестановок на некотором массиве длины лт будет равно лт
— 1, при этом число сравнений всегда будет одним и тем же;
Максимальное
количество перестановок на некотором массиве длины лт будет равно лт
— 1, при этом число сравнений всегда будет одним и тем же;
Пример 15. Пусть дан массив {З 4 5 1 2}.
![]()
После 1-й итерации получим {З 4 2 1 5} (4 сравнения, 1
перестановка). После 2-й итерации получим {З 1 2 4 5} (З сравнения, 1
перестановка). После 3-й итерации получим {2 1 З 4 5} (2 сравнения, 1
перестановка). После 4-й итерации получим {1 2 З 4 5} (1 сравнение, ![]() 1
перестановка).
1
перестановка).
Алгоритм окончен. Было сделано 4 + З + 2 + 10 сравнений и 4 перестановки.
В общем случае для обменной сортировки метод выбора верны следующие оценки:
из
![]()
|
Количество сравнений |
Количество присваиваний |
|
|
в любом случае
|
минимальное |
максимальное |
|
|
30—1) |
|
![]() Алгоритм сортировки выбором имеет квадратичную сложность
0(n2 ) относительно операций сравнения и линейную сложность О(п)
относительно операций перестановки.
Алгоритм сортировки выбором имеет квадратичную сложность
0(n2 ) относительно операций сравнения и линейную сложность О(п)
относительно операций перестановки.
Получив оценку сложности, мы можем сделать вывод, что данный алгоритм целесообразно применять, если операция обмена над элементами массива трудоемка, например если элементом массива является запись с большим числом полей.
4.7.3. Сортировка вставками
![]() Сортировка выбором и сортировка «пузырьком» относятся к
обменным сортировкам с убывающим шагом. Действительно, после выполнения каждой
итерации алгоритма количество элементов в неотсортированной части уменьшается
на единицу. Сортировка вставками построена на ином принципе.
Сортировка выбором и сортировка «пузырьком» относятся к
обменным сортировкам с убывающим шагом. Действительно, после выполнения каждой
итерации алгоритма количество элементов в неотсортированной части уменьшается
на единицу. Сортировка вставками построена на ином принципе.
Алгоритм сортировки вставками
Вначале упорядочиваются два первых
элемента массива. ![]() Они образуют начальное упорядоченное
множество S. Далее на каждом шаге берется следующий по порядку элемент и
вставляется в уже упорядоченное множество S так, чтобы слева от него все
элементы были не больше, а справа не меньше обрабатываемого. Место для вставки
текущего элемента в упорядоченное множество S ищется методом деления пополам.
Алгоритм сортировни заканчивает свою работу, когда элемент, первоначально
стоящий на п-м месте, будет вставлен на соответствующее ему место. (Именно
таким образом игроки
Они образуют начальное упорядоченное
множество S. Далее на каждом шаге берется следующий по порядку элемент и
вставляется в уже упорядоченное множество S так, чтобы слева от него все
элементы были не больше, а справа не меньше обрабатываемого. Место для вставки
текущего элемента в упорядоченное множество S ищется методом деления пополам.
Алгоритм сортировни заканчивает свою работу, когда элемент, первоначально
стоящий на п-м месте, будет вставлен на соответствующее ему место. (Именно
таким образом игроки ![]() обычно упорядочивают свои карты.)
обычно упорядочивают свои карты.) ![]()
Для алгоритма сортировки вставками верны следующие оценки:
![]()
|
Количество сравнений (при реализации бинарного поиска |
Количество присваиваний |
|
|
в любом случае 1 + 2 + [log23] + 1 + [logz х п— 1 + nlogrzn |
минимальное |
максимальное |
|
|
|
|
Алгоритм сортировки вставками имеет
квадратичную сложность О(п ) по числу присваиваний и сложность о ![]() по числу
сравнений.
по числу
сравнений.
Все рассмотренные выше алгоритмы сортировки имеют квадратичную сложность, по крайней мере по одному из параметров.
Вопрос: Можно ли и до какого предела улучшать алгоритм решения заДачи сортировки?
Ответ. Более эффективные алгоритмы
сортировки существуют. Сложность подобных универсальных алгоритмов составляет ![]() по
каждому из параметров.
по
каждому из параметров.
Для решения одной и той же задачи возможны самые разные подходы, анализ алгоритмов сортировки вскрывает сущность понятия сложности алгоритмов, а сравнение разных алгоритмов сортировки дает богатый материал для поиска путей совершенствования решений этой задачи. Почти все алгоритмы сортировки представляют несомненный практический интерес. Даже, казалось бы, не слишком эффективные прямые методы, и те в ряде случаев могут быть с успехом применены. При этом, к сожалению (или к счастью!), рекомендации на все случаи жизни дать нельзя. Чтобы выбрать самый подходящий для решаемой задачи алгоритм, необходимы знания, интуиция, творчество и опыт.
4.7.4. Сортировка слиянием
Рассмотренные алгоритмы сортировок вставками, выбором, «пузырьком» являются примерами алгоритма, действующего по шагам: в отсортированную часть добавляются новые элементы один за другим.
Рассмотрим алгоритм, основанный на другом подходе. Он основан на использовании метода «разделяй и властвуй» .
245
![]()
Многие алгоритмы по своей природе рекурсивны: решая некоторую задачу, они вызывают самих себя для решения ее подзадач. Идея метода «разделяй и властвуй» состоит как раз в этом. Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова. Наконец, их решения комбинируются и получается решение исходной задачи.
Для задачи сортировки эти три этапа выглядят следующим образом.
1. Сначала мы разбиваем массив на две половины.
2. Затем сортируем каждую из половин отдельно.
З. После этого соединяем два упорядоченных массива половинного размера в один.
Рекурсивное разбиение задачи на меньшие подзадачи происходит до тех пор, пока размер массива не дойдет до единицы: любой массив длины 1 можно считать упорядоченным.
Процесс сортировки слиянием показан на рисунке.
![]() Отсортированный
массив
Отсортированный
массив
|
1 |
2 2 3 4 5 |
Слияние
|
2 4 5 6 |
|
1 2 З |
Слияние
|
2 5 |
|
4 6 |
|
1 З |
|
2 6 |
Слияние Слияние
|
5 |
|
2 |
|
4 |
|
6 |
|
1 |
|
з |
|
2 |
|
6 |
Исходный массив
Вопрос. Как оценить время работы рекурсивного алгоритма?
Ответ. Время работы алгоритма складывается из времени, затрачиваемого на рекурсивные вызовы, которое можно выразить через некое рекуррентное соотношение. Далее следует оценить время работы, исходя из полученного соотношения.
![]()
Предположим, что алгоритм каждый раз
разбивает задачу размера п на а подзадач, каждая из которых имеет размерность в
Ь раз меньшую. Будем считать, что разбиение требует времени D(n), а соединение
полученных решений — С(п). Тогда для времени работы алгоритма Т(п) получаем
следующее рекуррентное соотношение ![]() (в худшем случае): Т(п) = аТ(п/Ь) + D(n)
+ С(п). Это соотношение выполняется для достаточно больших п, когда задачу
имеет смысл разбивать на подзадачи. Для маленьких п, когда такое разбиение или
невозможно, или не нужно, применяется какой-нибудь прямой метод решения.
Поскольку п ограничено (задача может состоять
(в худшем случае): Т(п) = аТ(п/Ь) + D(n)
+ С(п). Это соотношение выполняется для достаточно больших п, когда задачу
имеет смысл разбивать на подзадачи. Для маленьких п, когда такое разбиение или
невозможно, или не нужно, применяется какой-нибудь прямой метод решения.
Поскольку п ограничено (задача может состоять
![]()
![]() в сортировке очень
большого массива, но он все равно
в сортировке очень
большого массива, но он все равно ![]() конечен), время работы также не
превосходит некоторой константы.
конечен), время работы также не
превосходит некоторой константы.
![]() Пример 16. Подсчитаем
сложность алгоритма сортировки слиянием относительно операций сравнения. Для
простоты будем считать, что размер массива есть степень двойки. Тогда на каждом
шаге сортируемый массив делится пополам. Разбиение на части (вычисление границы
сортируемого массива) требует времени 0(1). Слияние двух отсортированных частей
в массив большей размерности п времени Оф). Тогда мы получаем следующее
рекуррентное соотношение для вычисления сложности алгоритма сортировки
слиянием:
Пример 16. Подсчитаем
сложность алгоритма сортировки слиянием относительно операций сравнения. Для
простоты будем считать, что размер массива есть степень двойки. Тогда на каждом
шаге сортируемый массив делится пополам. Разбиение на части (вычисление границы
сортируемого массива) требует времени 0(1). Слияние двух отсортированных частей
в массив большей размерности п времени Оф). Тогда мы получаем следующее
рекуррентное соотношение для вычисления сложности алгоритма сортировки
слиянием:
0(1), если п = 1, то![]()
2Т(п/2) + Оф), если п > 1.
Это соотношение влечет Т(п) = 0(nlog2n). Вывод этого равенства приведен в книге Т. Кормена и др. «Алгоритмы: построение и анализ».
Следовательно, для больших п сортировка слиянием эффективнее рассмотренных анее алгоритмов сортировки, имеющих сложность Оф ).
В заключение этеого параграфа скажем несколько слов о пользе быстрых алгоритмов. Часто разница между плохим и хорошим алгоритмами более существенна, чем разница между быстрым и медленным компьютерами. Приведем пример, аналогичный описанному в той же книге Кормена.
247
![]()
Пример 17. Требуется отсортировать массив из миллиона чисел. Что быстрее — сортировать его прямым выбором на компьютере, выполняющем 100 млн операций в секунду, или слиянием на компьютере, выполняющем 1 млн операций в секунду? Для сортировки п чисел выбором требуется только п 2 /2 операций сравнения. Алгоритм сортировки слиянием требует nlog2n операций сравнения.
При сортировке 1 млн чисел выбором получаем:
1/2 • (10 6 ) 2 операций
![]() =
5000 секунд 83 минуты.
=
5000 секунд 83 минуты.
10 8 операций в секунду
![]() При сортировке этого
же массива чисел слиянием получаем:
При сортировке этого
же массива чисел слиянием получаем:
![]() 10 6 •
log2 10 6 операций 20 секунд 1/3 минуты. О
10 6 •
log2 10 6 операций 20 секунд 1/3 минуты. О
![]()
10 6 операций в секунду
Вывод: разработка эффективных алгоритмов не менее важна, чем разработка быстрой электроники.
Вопросы и задания
1. Какие из описанных выше обменных алгоритмов работают быстро на почти упорядоченном массиве?
2. Укажите, какой массив надо подать на вход алгоритма сортировки вставками (N = 5), чтобы количество выполненных присваиваний было максимальным.
З. На вход алгоритма вставками подается массив {З 4 5 1 2}. Распишите, как изменяется массив в процессе выполнения алгоритма, аналогично примерам 13—15.
4. Требуется упорядочить по весу в возрастающем порядке лт непрозрачных банок с чаем, имея в своем распоряжении только чашечные весы без гирь. Напишите наиболее эффективный алгоритм решения этой задачи.
5. Тезис Чёрча
говорит о том, что класс вычислимых функ![]() ций совпадает с
классом рекурсивных функций. Запишите один из обменных алгоритмов сортировки в
виде рекурсивного алгоритма.
ций совпадает с
классом рекурсивных функций. Запишите один из обменных алгоритмов сортировки в
виде рекурсивного алгоритма.
6. Придумайте эффективный алгоритм одновременного поиска двух самых маленьких или самых больших элементов в неупорядоченном массиве.
![]()
Заключение
Научные открытия, новые идеи не возникают сами по себе, они рождаются в ответ на спрос, неудовлетворенную потребность. Как только математики высказали предположение, что некоторые задачи, быть может, не имеют решения (что само по себе являлось определенным научным достижением), математические исследования в данной области вышли на новый рубеж: а можно ли строго доказать, что рассматриваемая задача не имеег алгоритмического решения? В данном случае получение ответа на этот вопрос очень значимо: можно перестать тратить усилия и время на отыскание результата, который нельзя найти.
![]() Задача доказательства алгоритмической
неразрешимости привела к появлению другой задачи — построения формального
определения алгоритма. Математики очень долго пользовались интуитивным понятием
алгоритма, и оно их устраивало. Но для строгого доказатель
Задача доказательства алгоритмической
неразрешимости привела к появлению другой задачи — построения формального
определения алгоритма. Математики очень долго пользовались интуитивным понятием
алгоритма, и оно их устраивало. Но для строгого доказатель![]() ства
несуществования алгоритма надо знать, несуществование чего мы доказываем. А.
Тьюрингом и Э. Постом были предложены формальные определения алгоритмов в виде
абстрактных вычислительных конструкций. Достаточно простые по своей сути, эти
математические конструкции, названные в дальнейшем «машинами», оказались
универсальными вычислителями, на которых можно было реализовать любой известный
в математике алгоритм. Дальнейшие исследования в области теории
ства
несуществования алгоритма надо знать, несуществование чего мы доказываем. А.
Тьюрингом и Э. Постом были предложены формальные определения алгоритмов в виде
абстрактных вычислительных конструкций. Достаточно простые по своей сути, эти
математические конструкции, названные в дальнейшем «машинами», оказались
универсальными вычислителями, на которых можно было реализовать любой известный
в математике алгоритм. Дальнейшие исследования в области теории ![]() алгоритмов
привели к понятию вычислимой функции и вычислимости как таковой.
алгоритмов
привели к понятию вычислимой функции и вычислимости как таковой.
Более того, некоторые идеи из доказанной А. Тьюрингом в 1936 г. теоремы о существовании универсального вычислителя были использованы в дальнейшем (в 1940-х годах) при построении первого компьютера, а сам А. Тьюринг был одним из его разработчиков.
Мы проследили цепочку зарождения проблем и их решений, которые легли в основу целого раздела математики под названием «Теория алгоритмов», показали, по какому критерию из нескольких алгоритмов решения задачи следует выбирать лучший. Основные понятия теории алгоритмов достойны внимания как математиков, так и специалистов в области информатики. К таким понятиям следует отнести понятия алгоритма и вычислимой функции, понятие сложности алгоритма и ряд других.
Глава 5
![]()
Основы теории информации
![]()
Развитие математики вновь подтверждает, что деление науки на теоретическую часть и прикладную неправомерно. Наука едина, и можно говорить лишь о самой науке и ее возможных приложениях.
Н. Н. Боголюбов, М. А. Лаврентьев
S 5.1. Понятие информации. Количество информации.
Единицы измерения информации
S 5.2. Формула Хартли определения количества информации
S 5.3. Применение формулы Хартли
S 5.4. Закон аддитивности информации. Алфавитный подход к измерению информации
S 5.5. Информация и вероятность. Формула Шеннона
S 5.6. оптимальное кодирование информации и ее сложность
![]()
еория информации — сравнительно молодой
раздел математики — сформировалась как наука во второй половине ХХ века. Толчок
к зарождению ![]() этой науки дали попытки нахождения
оптимальных решений практических технических задач, в области кодирования и
передачи информации. Пионерами теории информации по праву считают Клода Шеннона
(США), А. Н. Колмогорова (СССР), Р. Хартли (США).
этой науки дали попытки нахождения
оптимальных решений практических технических задач, в области кодирования и
передачи информации. Пионерами теории информации по праву считают Клода Шеннона
(США), А. Н. Колмогорова (СССР), Р. Хартли (США).
S 5.1 . Понятие информации.
Количество информации. Единицы измерения ![]() информации
информации
![]() В данной главе мы
возвращаемся к понятию информации, уже неоднократно встречавшемуся ранее.
В данной главе мы
возвращаемся к понятию информации, уже неоднократно встречавшемуся ранее.
Информация — одно из фундаментальных понятий современной науки наряду с такими понятиями, как «вещество» и «энергия». Строгое определение этому термину дать невозможно. С точки зрения человека информация — это свеДения, обладающие такими характеристиками, как понятность, достоверность, новизна и актуальность (ценность).
Например, телефонный справочник обычно хранит информацию об абонентах городской телефонной сети. Однако если мы возьмем телефонный справочник г. Москвы за 1965 год, то сведения, в нем содержащиеся, будут по крайней мере не достоверны (за прошедшие с момента выпуска справочника годы изменились номера телефонов многих абонентов, многие учреждения оказались упраздненными, магазины закрытыми и т. д.). Следовательно, для абонента московской городской телефонной сети XXI века информации такой справочник почти не содержит.
В разных науках существуют различные формальные подходы к определению понятия информации. В информатине нас прежде всего интересуют два определения: сформировавшееся в математической теории информации и применяемое в computer science (данную отрасль научного знания обычно переводят на русский язык как информатика, однако последняя является более широким понятием, так как включает в себя и кибернетику, и моделирование, и ту же теорию информации, и многое другое).
![]()
Определение 1. Согласно американскому ученому и инженеру Клоду Шеннону, информация — это снятая неопреДеленность.
Шеннон впервые ввел такую трактовку в теории связи. Позднее она нашла применение во всех областях науки, где играет роль передача информации в самом широком смысле этого слова, в частности в математической теории информации, большую роль в становлении которой сыграл и великий российский ученый-математик А. Н. Колмогоров.
Согласно Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией, т. е. той частью сообщения, которая снимает полностью или уменьшает существовавшую до ее получения неопределенность какой-либо ситуации.
Определение 2. Величина неопределенности некоторого события — это количество возможных результатов (исходов) данного события.
Такой подход к определению информации называют содержательным. Так, например, неопределенность погоды на завтра обычно заключается в диапазоне температуры воздуха и возможности выпадения осадков. Причем в разное время года диапазон возможных исходов данного события различен и колеблется в районе 16 ожидаемых результатов для значения дневной температуры и трех-четырех — для осадков (без осадков, кратковременные дожди, ливень с градом и т. п.). Позднее мы покажем, какое количество информации несет достоверный прогноз погоды.
![]()
Вопрос. Зависит ли количество информации от того, кто и как фиксирует неопределенность соответствующей ситуации?
Ответ. У разных людей неопределенность знания о некотором
предмете может различаться. Так, неопределенность знания о погоде в Москве у
рядового американца и российского синоптика может различаться кардинально.
Поэтому содержательный подход к трактовке понятия информации часто является
субъективным. Если же число возможных исходов события не зависит от суждений
различных людей, то получаемая информация о наступлении одного из возможных
исходов является объективной. Примером такой информации явля![]() ется
сообщение о результате падения подброшенной монеты или игрального кубика.
ется
сообщение о результате падения подброшенной монеты или игрального кубика.
Вместе с тем, всякое сообщение (любые данные) можно закодировать с помощью конечной последовательности символов некоторого алфавита, С точки зрения информатики носителями информации являются любые последовательности символов, которые хранятся, переДаются и обрабатываются с помощью компьютера.
Определение З. Согласно Колмогорову, количество информации, содержащейся в последовательности символов, определяется минимально возможным количеством двоичных знаков, необходимых для кодирования этой последовательности безотносительно к содержанию представленного ею сообщения.
![]() Данный подход к
определению информации называют алфавитным. При этом для кодирования наиболее
часто используется двоичный алфавит, состоящий из нуля и единицы, это так
называемое двоичное кодирование информации. Смысл сообщения при этом может быть
учтен лишь на этапе выбора исходного алфавита для его записи либо не учтен
вообще. В частности, сообщения, записанные на естественном языке с помощью
соответствующего алфавита (например, сейчас вы читаете сообщение на русском
языке,
Данный подход к
определению информации называют алфавитным. При этом для кодирования наиболее
часто используется двоичный алфавит, состоящий из нуля и единицы, это так
называемое двоичное кодирование информации. Смысл сообщения при этом может быть
учтен лишь на этапе выбора исходного алфавита для его записи либо не учтен
вообще. В частности, сообщения, записанные на естественном языке с помощью
соответствующего алфавита (например, сейчас вы читаете сообщение на русском
языке,
А. Н. Колмогоров записанное с помощью русского же алфа(1903-1987)
вита), кодируются без учета их смыслового содержания. Такой подход является объективным.
На первый взгляд, определения 1 и З кажутся существенно различными. Тем не менее ниже будет показано, что они хорошо согласуются друг с другом.
Хотя информацию нельзя строго определить, ее можно измерить. Вернее, можно задать числом количество информации, подобно тому, как можно задать числом расстояние, время, массу, температуру и т. п. Чтобы стандартизировать измерение количества информации, договорились за единицу измерения брать бит (от английского binary digit).
Определение 4. При алфавитном подходе один бит это количество информации, которое можно передать в сообщении, состоящем из одного двоичного знака (О или 1). С точки зрения содержательного подхода один бит — это количество информации, уменьшающее неопределенность знания о предмете в два раза.
На практике чаще используется более крупная единица — байт, равная 8 битам. Так, один байт информации можно передать с помощью одного символа кодировки ASCII (см. S 2.3). Используются также следующие производные единицы измерения информации:
1 килобайт (1 Кб) — 2 10 байт 1024 байт;
1 мегабайт (1 Мб)![]() 2 20 байт - 1024 Кб
2 20 байт - 1024 Кб![]()
1 гигабайт (1 Гб)![]() 2 30 байт
2 30 байт![]() 1024 Мб
1024 Мб![]()
![]() 1
терабайт (1 Тб)
1
терабайт (1 Тб)![]() 2 40 байт
2 40 байт![]() 1024 Гб
1024 Гб ![]() Для
вопросов хранения и передачи информации более важным является не количество
информации, а ее объем.
Для
вопросов хранения и передачи информации более важным является не количество
информации, а ее объем.
Определение 5. Информационным объемом сообщения называется количество двоичных символов, которое используется для кодирования этого сообщения.
В отличие от определения количества
информации (определение З), в данном случае не требуется, чтобы число двоичных
символов было минимально возможным. Размер текстовых файлов, в которых
сообщение на английском языке записано в ЉСП-кодировке, характеризует именно
информационный объем соответствующего текста, а не количество информации в нем,
даже в смысле алфавитного подхода. При оптимальном кодиро![]() вании, речь о котором
пойдет ниже, понятия количества информации и информационного объема совпадают.
вании, речь о котором
пойдет ниже, понятия количества информации и информационного объема совпадают.
Вопросы и задания
1.
2. Приведите пример, когда алфавитный подход к трактовке понятия информации оказывается субъективным.
З. При игре в кости используются два игральных кубика, грани которых помечены числами от одного до шести. В чем заключается неопределенность знания о бросании одного кубика? А двух кубиков одновременно?
4. Сколько гигабайт содержится в 2 18 килобайтах? Сколько мегабайт содержится в 2 20 килобитах?
5. Вспомните различные жизненные ситуации, при которых мы получаем ровно один бит информации.
S 5.2. Формула Хартли определения количества информации
Процесс измерения количества информации можно объяснить на примере известной игры в угадывание. Согласно правилам этой игры, один из участников должен отгадать предмет (или одно из возможных состояний некоторого предмета), который задумал кто-то другой. При этом допускается только два вида ответов: «да» и «нет». В данном случае ответ на один вопрос несет один бит информации, так как из двух возможных исходов выбирается один.
Задача 1. Предположим, что в классе находятся 32 ученика, и учитель решил спросить одного из них. Какое минимально возможное количество вопросов нам надо заДать учителю, чтобы наверняка опреДелить, кого именно он решил спросить?
Записав полученные ответы и заменив все ответы «да» единицами, а «нет» — нулями, мы получим сообщение в виде последовательности из пяти двоичных цифр.
Способ 2. Отгадывать школьника можно было и по-другому. Присвоим каждому школьнику номер от О до 31. Запишем номера в двоичной системе счисления. Самые длинные номера состоят - из пяти двоичных цифр. Дополним остальные номера до пяти цифр слева нулями. Далее вопросы учителю можно задавать так: «Верно ли, что первая слева цифра в номере задуманного ученика равна единице?» , «Верно ли, что вторая цифра в номере задуманного ученика равна единице?» и т. д. Предположим, что ответы на вопросы были: «нет», «да», «нет», «нет», «да». Тогда мы сразу определим, что номер загаданного ученика 010012 9.
В обеих процедурах определения загаданного ученика длина получаемого сообщения равна пяти двоичным символам, т. е. в результате угадывания мы получаем 5 бит информации.
Мы увидели, что для отгадывания
задуманного учени![]() ка из 32 школьников Достаточно задать 5
вопросов указанного выше вида. Но если задавать вопросы не лучшим образом,
может случиться так, что необходимо не 5, а, скажем, 7 вопросов. Казалось бы,
что так как каждый вопрос подразумевает один из двух возможных ответов, то,
получив ответы на первые 5 вопросов, мы всегда получим 5 бит информации. Однако
это не всегда справедливо. Как же происходит «недостача» информации?
ка из 32 школьников Достаточно задать 5
вопросов указанного выше вида. Но если задавать вопросы не лучшим образом,
может случиться так, что необходимо не 5, а, скажем, 7 вопросов. Казалось бы,
что так как каждый вопрос подразумевает один из двух возможных ответов, то,
получив ответы на первые 5 вопросов, мы всегда получим 5 бит информации. Однако
это не всегда справедливо. Как же происходит «недостача» информации?
Дело в том, что при неразумном выборе
вопросов может получиться так, что какие-либо два вопроса, ответ на каждый из
которых несет один бит информации, в сумме содержат меньше двух бит информации.
Это возможно, если ответ на первый вопрос полностью или частично содержит ответ
на второй. Например, если сначала спросить, не равна ли первая цифра в номере
ученика нулю, а потом — не равна ли она единице, то второй ответ не до![]() бавляет ровно никакой информации, и общее количество информации в двух ответах
равно одному биту, а не
бавляет ровно никакой информации, и общее количество информации в двух ответах
равно одному биту, а не ![]() двум. Отсюда напрашивается следующий
вывод.
двум. Отсюда напрашивается следующий
вывод.
![]() В результате приходим к следующему
определению.
В результате приходим к следующему
определению.
Определение 6. Для того чтобы измерить количество информации в сообщении, надо закодировать сообщение в виде последовательности нулей и единиц наиболее рациональным способом, позволяющим получить самую короткую последовательность. Длина полученной последовательности нулей и единиц и является мерой количества информации в битах.
Вопрос. Пусть для коДирования всех возможных ИСХОДОВ некоторого события были использованы Двоичные послеДовательности длины К. Означает ли это, что количество информации в сообщении о наступлении одного из исходов Данного события равно К?
Ответ. Вернемся к задаче 1 в случае, когда надо выбирать задуманного ученика уже среди 24 человек. В этом случае нам понадобится не меньше 4 и не больше 5 вопро-
сов, если действовать методом деления пополам. После третьего вопроса у нас останется трое «подозреваемых» . Их можно разделить на группу из одного и группу из двух учеников. Тогда после четвертого вопроса мы либо сразу найдем нужного школьника, либо придется задавать пятый вопрос.
Попробуем действовать вторым способом. Закодируем номера 24 школьников двоичными номерами от 000002 до 101112. Содержит ли закодированный номер 5 бит информации? Нет, не совсем так. Длина кодовой последовательности здесь та же, что и раньше, но число различных номеров меньше. Поэтому, например, если мы узнаем, что старшая цифра номера равна 1, то вопрос о второй слева цифре задавать не придется (объясните почему), и мы сумеем определить номер искомого ученика, задав 4 вопроса, а не 5. Значит, количество информации, требуемой, чтобы выбрать задуманного ученика из 24 человек, больше 4 бит и меньше 5 бит.
Лемма 1. Число различных двоичных слов длины К равно 2 .
Доказательство. Докажем данное
утверждение индукцией по длине последовательности К. Для К = 1 утверждение
очевидно. Пусть уже доказано, что число двоичных слов длины К равно 2 . Все
двоичные слова длины К + 1 делятся на два типа: начинающиеся с нуля и
начинающиеся с единицы. Выпишем все слова длины К, в силу предположения
индукции их 2 k . Припишем к каждому из них слева ноль. Ниже выпишем
все слова длины К снова и припишем к ним слева единицу. Так мы записали все
слова длины К + 1. Таким образом число последовательностей длины К + 1 равно 2
+ 2 2k+1 ![]() Лемма Доказана.
Лемма Доказана.
Определение 7. ДВОИЧНЫМ коДированием множества лт называется отображение, ставящее в соответствие каждому элементу множества лк его двоичный код: последовательность нулей и единиц. Кодирование называется однозначным, если коды различных элементов множества лт различны.
Лемма 2. Множество лт допускает однозначное двоичное кодирование с длинами кодов, не превосходящими К, в том и только в том случае, когда число элементов множества лт не превосходит 2 .
Доказательство. Одно множество можно
однозначно отобразить в другое множество, только если число элемен![]() тов первого
тов первого ![]() не
превышает числа элементов второго множества. Так как по лемме 1 число двоичных
слов длины К равно 2 , то доказываемое утверждение справедливо.
не
превышает числа элементов второго множества. Так как по лемме 1 число двоичных
слов длины К равно 2 , то доказываемое утверждение справедливо.
Лемма Доказана.
Задача 2, Рассмотрим следующую проблему коДирования
результатов голосования. Пусть имеются три варианта ![]() голосования: «за»,
«против», «воздержался». Требуется закоДировать результаты ГОЛОСОВС[НИЯ,
содержащиеся в N бюллетенях.
голосования: «за»,
«против», «воздержался». Требуется закоДировать результаты ГОЛОСОВС[НИЯ,
содержащиеся в N бюллетенях.
Решение. Результаты можно было бы кодировать с помощью двухбитовых слов, например 11, 00, 01. При этом комбинация 10 остается неиспользованной. При таком кодировании лк результатов голосования займут объем 2N бит памяти. Для того- чтобы улучшить этот результат; будем кодировать блоки из трех бюллетеней. Тогда число вариантов голосования для тройки бюллетеней равняется З • З • З = 27 < 2 0 , т. е. в данном случае возможно пятибитовое кодирование. Так как число троек равно N/3, а каждая из них займет 5 бит памяти, то для хранения понадобится уже 5N/3 бит памяти.
Но и этот результат можно улучшить, если составить блоки из
5 бюллетеней. В этом случае число исхоаов голосования для блока составляет З
243 < 256 = 2 и его можно записать в один байт. Таким образом, на бюллетень
придется 8/5 бита памяти. ![]()
Вывод, к которому мы пришли при решении задачи 2, позволяет нам вывести следующую формулу, называемую формулой Хартли.
![]() Р. Хартли (1888—1970); область
научных интересов: радиоэлектроника, теория информации. Первым ввел понятие
информации как переменной величины и попытался ввести меру количества
информации.
Р. Хартли (1888—1970); область
научных интересов: радиоэлектроника, теория информации. Первым ввел понятие
информации как переменной величины и попытался ввести меру количества
информации.
Формула Хартли
Количество информации, которое вмещает один символ Г№-элементного алфавита, равно logzN.
По-другому это же утверждение можно
сформулировать так. Количество информации, полученное при выборе одного
предмета из лк равнозначных предметов, равно log2N. То есть именно
такое количество информации необходимо для устранения неопределенности из ![]() равнозначных
вариантов.
равнозначных
вариантов.
Доказательство. Для алфавита из дт различных символов можно составить всех возможных слов длины т (доказывается аналогично лемме 1). Пусть К таково, что
![]()
То есть количество информации, содержащееся в одном символе этого алфавита, заключено между К/т и (К + 1)/m. Логарифмируя неравенства (5.1), получаем:
К < mlog2N К + 1.
Разделив неравенства (5.2) на т, делаем вывод, что разность между количеством информации, которое несет один символ 1У-элементного алфавита, и log2N не превосходит 1 / т для любого т. Значит, при оптимальном двоичном кодировании такого символа (которое при росте т достижимо с какой угодно точностью) средняя длина слова составит log2N.
Вопросы и задания
1. В библиотеке 16 стеллажей, в каждом стеллаже 8 полок. Какое количество информации несет сообщение о том, что нужная книга находится на четвертой полке?
2. Была
получена телеграмма: «Встречайте вагон 7 поезд N2 32». Какое количество
информации получил адресат, если известно, что в этот город приходят 4 поезда,
а в каждом поезде в среднем 16 вагонов? ![]()
З. Сколько информации получит ученик,
если в 10-00 увидит сообщение о том, что классный час состоится в 14 ча![]() сов,
при условии, что в этот день всегда бывает классный час? Ответ обоснуйте.
сов,
при условии, что в этот день всегда бывает классный час? Ответ обоснуйте.
4. Почему множество ASCII-c№IMB0J10B образует алфавит, состоящий именно из 256 символов? Сколько вопросов надо задать, чтобы отгадать один из символов этого алфавита?
5. В классе четыре ряда парт по четыре парты в каждом ряду. Каждая парта имеет два места. Все места на партах заполнены учениками. Учитель задумал одного из них. Какое количество информации мы получим, если зададим два следующих вопроса и получим на них положительный ответ?
Вопросы:
Сидит ли задуманный ученик на первых двух рядах? Сидит ли задуманный ученик на первой или второй парте?
6. Верно ли, что для любого т при организации в задаче 2 т-блочного кодирования результатов голосования (т + 1)блочное кодирование всегда ближе к оптимальному, чем т-блочное?
7. Докажите, что для алфавита из Лт различных символов можно составить всех возможных слов длины т,
S 5.3. Применение формулы Хартли
Пример 1. В задаче 2 из предыдущего параграфа шла речь о кодировании результатов голосования. При этом каждый бюллетень содержал в себе один из трех возможных исходов голосования. Если за единицу измерения количества информации принять количество информации, которое можно передать одним символом трехсимвольного алфавита (например, «+» , «—», «О»), что соответствует уменьшению неопределенности в три раза, то каждый бюллетень будет содержать ровно одну такую единицу количества информации.
В формуле Хартли логарифм можно брать по
любому основанию, это равносильно выбору единицы из![]() мерения количества
информации.
мерения количества
информации.
![]() Пример 2. Введенная в примере 1 единица измерения
количества информации удобна и при анализе результатов взвешивания на
двухчашечных весах. Как известно, каждое такое взвешивание может привести к
одному из трех результатов: тяжелее оказывается груз на левой чаше весов,
тяжелее груз на правой чаше или весы находятся в равновесии. В данном случае
результатом одного взвешивания может являться количество информации, большее,
чем бит 2
Пример 2. Введенная в примере 1 единица измерения
количества информации удобна и при анализе результатов взвешивания на
двухчашечных весах. Как известно, каждое такое взвешивание может привести к
одному из трех результатов: тяжелее оказывается груз на левой чаше весов,
тяжелее груз на правой чаше или весы находятся в равновесии. В данном случае
результатом одного взвешивания может являться количество информации, большее,
чем бит 2 ![]() Пусть у нас имеется ЛГ монет,
одна из которых фальшивая (легче остальных). К взвешиваний дают klog23 бит
информации и не могут снять неопределенность, ббль
Пусть у нас имеется ЛГ монет,
одна из которых фальшивая (легче остальных). К взвешиваний дают klog23 бит
информации и не могут снять неопределенность, ббль![]() шую, чем log23 k
, поэтому для определения фальшивой монеты потребуется не менее log
N/log23 = К взвешиваний. Здесь К — количество информации в единицах, введенных
в примере 1.
шую, чем log23 k
, поэтому для определения фальшивой монеты потребуется не менее log
N/log23 = К взвешиваний. Здесь К — количество информации в единицах, введенных
в примере 1.
Известно, что эта задача как раз и разрешима ровно за три взвешивания.
Пример З. Задача поиска фальшивой монеты становится 60лее сложной, если заранее неизвестно, легче она или тяжелее остальных монет. В этом случае число различных исходов изначально равно 2N (каждая монета может оказаться фальшивой и быть как легче остальных, так и тяжелее). Значит, для решения задачи понадобится не менее log22N/log23 взвешиваний. Таким образом, за три взвешивания мы теперь сможем исследовать не более 13 монет (2N < 27). 2
Поиск алгоритма решения такой задачи сложен и для меньшего числа монет.
Задание. Попробуйте решить эту задачу самостоятельно для 12 монет, и вы убеДитесь, что это совсем не просто, а порой вообще кажется невозможным.
Решение. Для решения задачи нужно использовать такую операцию, как перекладывание монеты с одной чаши весов на другую. Введем следующие обозначения. Монету, обозначенную знаком «+» , во время текущего взвешивания следует положить на весы, причем если она на весах уже была, то на ту же самую чашу, на которой эта монета находилась во время своего предыдущего взвешивания. Монету, обозначенную знаком «—», следует переложить на противоположную чашу весов по отношению К той, на которой она находилась. Заметим, что если монета на весах еще не была, то знак «—» к ней применен быть не может. Наконец, монеты, обозначенные знаком «О», в очередном взвешивании не участвуют.
Составим таблицу путем выписывания всех возможных вариантов расположения символов «+» , «—» и «О» в столбцах, соответствующих монетам. Недопустимые варианты: знак «—» расположен выше знака «+» . Каждый столбец описывает местонахождение соответствующей ему монеты во время каждого из трех взвешиваний.
1 2 з 4 5 6 7 8 9 10 11 12 13 14
![]() + + + + -9 + + + О О О О О первое взвешивание
+ + + + -9 + + + О О О О О первое взвешивание
-4- О
О О + + + О О второе взвешивание ![]() третье взвешивание
третье взвешивание
Результат каждого взвешивания в
отдельности никак не анализируется, а просто записывается. При этом равновесие
на весах всегда кодируется нулем, впервые возникшее неравновесное состояние
знаком «плюс» . Если при следующем взвешивании весы отклонятся от равновесия в ту
же самую сторону, то результат такого взвешивания также кодируется плюсом, а
если в другую сторону, то минусом. Например, следующие результаты взвешиваний
«=<<» и «=>>» кодируются как «0++» ![]() а результатЫ « и
а результатЫ « и ![]() —
как «+0—». Так как мы не знаем, легче или тяжелее остальных монет окажется
—
как «+0—». Так как мы не знаем, легче или тяжелее остальных монет окажется ![]() фальшивая
монета, то нам важно, как изменялось состояние весов от взвешивания к
взвешиванию, а не то, какая именно чаша оказывалась тяжелее, а какая легче.
Поэтому два на первый взгляд различных результата трех взвешиваний в этом
случае кодируются одинаково.
фальшивая
монета, то нам важно, как изменялось состояние весов от взвешивания к
взвешиванию, а не то, какая именно чаша оказывалась тяжелее, а какая легче.
Поэтому два на первый взгляд различных результата трех взвешиваний в этом
случае кодируются одинаково.
После подобной записи результатов взвешиваний фальшивая монета уже фактически определена. Ею оказывается та, которой соответствует такой же столбец в таблице, как и закодированный нами результат трех взвешиваний. Для первого примера это монета, которая участвовала во взвешиваниях по схеме, указанной в 10-м столбце таблицы, а для второго — в 8-м. В самом деле, состояние весов в нашей задаче меняется в зависимости от того, где оказывается фальшивая монета во время каждого из взвешиваний. Поэтому монета, «поведение» которой согласуется с записанным результатом взвешиваний, такой результат и определяет.
В главе 4 приведено несколько различных алгоритмов сортировки массивов, количество операций сравнения в которых для худшего случая различно. Некоторые из них являются более эффективными по числу производимых сравнений.
Вопрос. Какова сложность алгоритмов сортировки, оптилшЛЬНЫХ по числу сравнений?
Ответ. Ответ и на этот вопрос может дать теория информаЦИИ.
Отсортировать произвольный массив с точки зрения теории информации это
значит найти одну из ![]() • лт перестановок всех элементов данного массива. Сравнения
элементов между собой в данном
• лт перестановок всех элементов данного массива. Сравнения
элементов между собой в данном
случае соответствуют задаваемым вопросам с возможными
вариантами ответа «да» или «нет». Тогда по формуле Хартли для сортировки
элементов в худшем случае потребуется получить не менее log N! бит информации,
т. е. произвести не менее log N! операций сравнения элементов между собой. Для
оценки значения N! при больших N в математике применяют формулу Стирлинга: ![]()
![]() 21INNNe
21INNNe![]()
Вопросы и задания
1. Объясните, как, используя формулу Хартли, можно сразу измерить любую, например графическую, информацию в байтах, а не в битах?
2. В анкете предлагаются следующие варианты ответа на вопрос о степени владения английским языком: «не владею», «читаю со словарем», «могу объясняться», «владею хорошо», «могу переводить синхронно» . Какое количество информации несет ответ на данный пункт анкеты? Предложите различные способы кодирования ответов на этот вопрос анкеты, при условии, что обработке подлежит большое количество подобных анкет.
З. В некоторых карточных играх используется колода из 32 карт. Придумайте карточный фокус, в результате КОТОР0го ведущий, задав небольшое количество вопросов, определяет загаданную зрителями карту. Какое количество информации необходимо с точки зрения теории информации, чтобы отгадать карту? Какое количество информации несут ответы на заданные вопросы?
4. Докажите, что гарантированно найти одну фальшивую монету среди 1000 монет, если известно, что она легче, меньше чем за 7 взвешиваний нельзя.
5, Объясните с точки зрения теории информации, почему задачу поиска фальшивой монеты из двух имеющихся монет решить нельзя, если неизвестно, легче или тяжелее она настоящей монеты.
6. Выведите формулу для числа взвешиваний, необходимых для гарантированного нахождения фальшивой монеты среди N монет, если неизвестно, легче или тяжелее она остальных монет.
7. ![]()
S 5.4. Закон амитивности информации. Алфавитный подход к измерению информации
Пусть нам теперь необходимо отгадать сразу два независимых предмета х1 и ху про которые известно, что х1 принадлежит множеству Х 1 , содержащему N1 элементов, а х2 принадлежит множеству Х2 , содержащему N2 элементов. Вполне допустимо считать, что мы должны угадать пару (хр х2) во множестве Х всех возможных пар (хр х2), где .х1 е Х 1 , а х2 е Х2. Тогда по формуле Хартли для угадывания задуманной пары необходимо задать log2NIN2 вопросов, т. е. получить log2N1N2 бит информации. Вместе с тем, элементы х1 и х2 можно угадывать независимо. Для угадывания х1 нам понадобится logzN1 вопросов, а для угадывания х2 log2N2. Всего при этом понадобится log2N1 + log2N2 вопросов (бит информации).
Мы получили два выражения для одного и того же количества информации. Согласно основному логарифмическому тождеству, обе величины равны: log2N1N2 = log2N1 + log2N2.
Переформулировав данное тождество в терминах количества информации, мы получаем следующий закон.
Закон аддитивности информации. Количество
информации Н(х х ) необходимое для установления пары (х 1 , х», равно сумме
количеств информации н(х1) и н(х2), не![]() обходимых для независимого установления
элементов х 1 и хы.
обходимых для независимого установления
элементов х 1 и хы.
НА, х» = Н(хр + н(х2). (5.3)
![]() Пример 4. Используя
закон аддитивности информации и формулу Хартли, подсчитаем, какое количество
информации несет достоверный прогноз погоды.
Пример 4. Используя
закон аддитивности информации и формулу Хартли, подсчитаем, какое количество
информации несет достоверный прогноз погоды.
следующий день заключается в предсказании дневной
температуры (обычно вы![]() бор делается из 16 возможных для данного
сезона значений) и одного из четырех значений облачности (солнечно,
бор делается из 16 возможных для данного
сезона значений) и одного из четырех значений облачности (солнечно,
переменная облачность , пасмурно, дождь).
Получаемое при этом количество информации равно log216 + log24 = 4 + 2 = 6 бит.
Закон аддитивности информации справедлив и при алфавитном подходе к измерению информации.
Напомним, что кодирование информации
(сообщений) в рамках алфавитного поДхоДа осуществляется ![]() следующим образом.
Для записи сообщений определенного вида вводится свой алфавит (набор символов).
Количество различных символов в алфавите называется его мощностью. Алфавит
вводится так, чтобы любое сообщение интересующего нас вида можно было бы
записать только с помощью конечной последовательности символов данного
алфавита.
следующим образом.
Для записи сообщений определенного вида вводится свой алфавит (набор символов).
Количество различных символов в алфавите называется его мощностью. Алфавит
вводится так, чтобы любое сообщение интересующего нас вида можно было бы
записать только с помощью конечной последовательности символов данного
алфавита.
Определение 8. Количество информации, содержащееся в одном символе, называется его информационным весом. Согласно формуле Хартли, этот вес равен log2N.
В S 5.2 уже был приведен пример
минимального алфавита, с помощью которого можно записывать практически
произвольные сообщения на английском языке. Но понятие алфавита вовсе не
обязательно связано с алфавитами естественных языков (английского, русского, корейского
и т. д.). Так, для записи чисел в позиционных системах счисления используется
алфавит, мощность которого равна основанию системы счисления Р (см. главу 1).
Информационный вес символа такого ал![]() фавита (цифры) равен log2P. Для записи
пола человека в анкетах обычно используется двухсимвольный алфавит («м», «ж»
или «т», «f»). А для кодирования различных состояний облачности можно
использовать четыре фиксированных рисунка, каждый из которых будет представлять
собой символ с информационным весом log24 2
фавита (цифры) равен log2P. Для записи
пола человека в анкетах обычно используется двухсимвольный алфавит («м», «ж»
или «т», «f»). А для кодирования различных состояний облачности можно
использовать четыре фиксированных рисунка, каждый из которых будет представлять
собой символ с информационным весом log24 2
![]()
Пример 5. Одна страница художественного прозаического произведения на английском языке может содержать около 2400 символов, включая разделительные пробелы между словами. Тогда для эффективного хранения подобной страницы текста в компьютере понадобится 2400 log232 бит = 12000 бит = 1500 байт памяти вместо 2400 байт при АМ)П-представлении текстовой информации.
Пример 6. Для компьютерной записи столетних наблюдений о погоде, касающихся облачности в Москве, потребуется около 365 + 25•366) бит 73 050 бит памяти. Столько же вопросов нам придется задать синоптику, чтобы узнать состояние облачности во все дни рассматриваемого столетия.
Вопросы и задания
1. Выполните упражнение 2 к S 5.2, используя закон аддитивности информации.
2. Определите количество информации в своей фамилии при условии, что для кодирования фамилий будет использоваться 32-символьный алфавит.
З. Алфавит некоторого языка состоит из 32 символов. За сколько секунд мы сможем передать текст из 1600 оптимально закодированных символов этого алфавита, если скорость передачи составляет 100 байт в секунду?
4. В течение 5 секунд было передано сообщение, объем которого составил 375 байт. Каков размер алфавита, с помощью которого записано сообщение, если скорость передачи составила 200 символов в секунду?
5. При игре в КОСТИ используют 2 одинаковых кубика, грани которых помечены числами от 1 до 6. Сколько информадии несет сообщение о том, что при бросании двух кубиков в сумме выпало 12 очков?
6.
S 5.5. Информация и вероятность. Формула Шеннона
Для определения количества информации
далеко не всег![]() да возможно использовать формулу Хартли.
Ее применя
да возможно использовать формулу Хартли.
Ее применя![]() ют лишь в частном случае, когда выбор
любого элемента из множества, содержащего лт элементов, равнозначен.
Или, при алфавитном подходе, все символы алфавита встречаются в сообщениях,
записанных с помощью этого алфавита, одинаково часто. Однако в действительности
так бывает далеко не всегда. В том числе и символы алфавитов естественных
языков в сообщениях появляются с разной частотой.
ют лишь в частном случае, когда выбор
любого элемента из множества, содержащего лт элементов, равнозначен.
Или, при алфавитном подходе, все символы алфавита встречаются в сообщениях,
записанных с помощью этого алфавита, одинаково часто. Однако в действительности
так бывает далеко не всегда. В том числе и символы алфавитов естественных
языков в сообщениях появляются с разной частотой.
Лемма З. Пусть наш алфавит состоит из двух символов (а и Ь), но множество символов сообщения содержит п экземпляров символа а и т экземпляров символа Ь. Тогда, если нам встретится символ а, мы получаем log2(m + п) — log2n бит информации, а в случае встречи символа Ь log2(m+ п) logyn бит информации.
Доказательство. Рассмотрим новый
алфавит из п + т символов: а а![]() Ь . В новом алфавите каждый символ
встречается уже с равной частотой и его информационный вес выражается формулой
log2(n + т). Если при встрече некоторого а. мы бы распознавали его
уникальность, то мы бы получили log2n бит информации, так как таких символов п.
Но все символы а. одинаковы, и нам не важно, какой именно символ а. нам
встретился, и определять это мы не будем. Поэтому в резулътате отождествления
всех символов а. мы недополучаем (теряем) log2n бит информации, если
встречается
Ь . В новом алфавите каждый символ
встречается уже с равной частотой и его информационный вес выражается формулой
log2(n + т). Если при встрече некоторого а. мы бы распознавали его
уникальность, то мы бы получили log2n бит информации, так как таких символов п.
Но все символы а. одинаковы, и нам не важно, какой именно символ а. нам
встретился, и определять это мы не будем. Поэтому в резулътате отождествления
всех символов а. мы недополучаем (теряем) log2n бит информации, если
встречается ![]() один из символов а. Следовательно,
полученное количество информации равно log2(m + п) — log№ бит. Аналогично, мы
теряем loggn бит информации, если встречается символ Ь.
один из символов а. Следовательно,
полученное количество информации равно log2(m + п) — log№ бит. Аналогично, мы
теряем loggn бит информации, если встречается символ Ь.
Лемма Доказана.
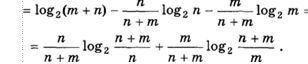
Назовем частотой встречаемого символа а в некотором множестве символов величину р = п /N, где N — общее количество символов в множестве, а п — количест-
а
во символов а в этом же множестве.
Тогда частота Р1 появления символа а в нашем множестве равна п/(п + т). Аналогично Р2 = т/(п + т). При этом + = 1. В этих терминах средний информационный вес символа двухсимвольного алфавита выражается
формулой
Н = p110g2(1/p1) + p210g2(1/p2).
Это и есть формула Шеннона для алфавита, состоящего из двух символов.
Пусть у нас есть источник информации, который выдает последовательность символов некоторого алфавита,
при этом разные символы могут появляться с разной частотой. Обозначим пф) количество символов а среди N символов последовательности.
Определение 9. Если при увеличении длины последовательности п величина n(a)/N стремится к некоторому числу Ра, то это число называется вероятностью появления символа а из данного источника.
Для конечных последовательностей понятие вероятности просто совпадает с понятием частоты появления данного символа среди множества символов последовательности. Выведем теперь формулу Шеннона для случая У-символьного алфавита.
Формула Шеннона
![]() + p210g2(1/p2) + ... + pNlog2(1/py).
(5.4)
+ p210g2(1/p2) + ... + pNlog2(1/py).
(5.4)
![]() Доказательство. Для
лт = 2 формула уже доказана. Пусть формула верна для любого
алфавита, состоящего из — 1 символа. Отождествим два последних символа нашего
алфавита. Вероятность появления любого из этих двух символов равна (PN_1 + П).
Тогда мы имеем алфавит, состоящий из лт — 1 символа, К. Шеннон и, по
предположению, средний информацион(1916-2001) ный вес будет выражаться так:
Доказательство. Для
лт = 2 формула уже доказана. Пусть формула верна для любого
алфавита, состоящего из — 1 символа. Отождествим два последних символа нашего
алфавита. Вероятность появления любого из этих двух символов равна (PN_1 + П).
Тогда мы имеем алфавит, состоящий из лт — 1 символа, К. Шеннон и, по
предположению, средний информацион(1916-2001) ный вес будет выражаться так:
![]() +
p210g2(1/p2) + ... +
+
p210g2(1/p2) + ... +
+ (PN-1 + + PN))•
Определим, как часто среди двух
отождествленных символов будет появляться каждый из них в отдельности. Такие
частоты назовем относительными вероятностями появления каждого из двух
символов. Они равны qN-1 = PN-1/(PN-1 + И = PN/(PN-1 +![]()
Согласно лемме З,
при отождествлении мы потеряли ![]() + qNlog21/qN
+ qNlog21/qN
бит информации на каждый из отождествленных символов, а их доля среди всех символов составляет PN_1 + рлт. Следовательно, в среднем на один символ потеряно
![]() PN-110g21/qN_1 + pNlog21/qN бит.
PN-110g21/qN_1 + pNlog21/qN бит. ![]()
Если прибавить полученное выражение к формуле (5.5), то после несложных преобразований мы и получим формулу Шеннона.
Формула Шеннона Доказана.
Л. Больцман пример состояния молекул газа, образую-
(1844-1906) щих систему. Эта интерпретация позволяет легко понять, почему Больцман получил такую же формулу, какую Шеннон получил для информации.
Вопрос. Согласуются ли межДу собой формулы Хартли и Шеннона?
Ответ. Чтобы ответить на этот вопрос, применим формулу Шеннона к алфавиту, символы которого в сообщениях равновероятны. То есть = Р2 — = 1/N. Тогда формула Шеннона примет вид
Н = (1/N)log2N + (1/N)log2N + ... + (1/N)log2N = log2N,
т. е. совпадет с формулой Хартли.
Вопрос. Всегда ли ответ «да» или «нет» (а в алфавитном поДхоДе один символ Двухсимвольного алфавита) соДержит ровно один бит информации?
Ответ. Рассмотрим формулу Шеннона в
случае лт = 2. Если вероятность одного ответа равна р, то другого ![]()
Тогда формулу Шеннона можно рассматривать как функцию одной переменной:
Нф) = plog21/p + (1 — ![]() — р).
— р).
Исследуя производную этой функции, несложно доказать, что максимум Нф) на отрезке [О, 1] равен 1 и достигается при р = 1/2. Следовательно, один бит информации мы получаем только в том случае, когда ответы «да» и «нет» равновероятны. Так, сообщение о том, что бутерброд упал маслом вниз, несет в себе менее одного бита информации (как известно, бутерброд со стола на пол практически всегда падает маслом вниз). Более того, если мы будем бросать бутерброд несколько раз, а результаты наших экспериментов будем записывать с помощью 0 и 1, то и в среднем один символ полученного двоичного кода будет нести менее одного бита информации.
![]() Формула Шеннона показывает средний информационный вес
символов того или иного алфавита или энтропию распределения частот появления
символов соответствующего алфавита.
Формула Шеннона показывает средний информационный вес
символов того или иного алфавита или энтропию распределения частот появления
символов соответствующего алфавита.
Дело обстоит проще, если нас интересует количество информации, которое несет тот или иной символ в отдельности (или же, что то же самое, количество вопросов, которое придется задать, чтобы отгадать предмет, вероятность нахождения которого в данном множестве известна). Причем при выводе соответствующей формулы используются те же соображения, что и при выводе формулы Шеннона.
Пусть в нашем множестве находится N предметов. При этом интересующий нас предмет является одним из т N одинаковых предметов. То есть вероятность его появления есть р = m/N. Если каждый предмет нашего множества считать уникальным, то по формуле Хартли его можно угадать в среднем за log2N вопросов. Но в данном случае, угадав любой из интересующих нас предметов, мы зададим на logwn вопросов меньше, так как
не будем определять, какой именно экземпляр нам подался.
Общее число вопросов при этом будет выражаться формулой log2N — loggn = log2N/m
= log21/p. ![]()
Формула (5.6) верна и в случае, если все N предметов во множестве уникальны (т. е, имеется .N различных предметов), но вероятности их появления различны. Для вывода формулы в этом случае используются те же рассуждения, что и при доказательстве леммы З.
Задача З. В результате многолетних наблюдений учитель информатики знает, что у половины его учеников итоговой отметкой за год будет «четверка», у 1/4 учеников — «пятерка», у 1/8 — «тройка», а остальные ученики по разным причинам окажутся неаттестованными. Какое количество информации мы получим после того, как узнаем, какую именно отметку получил уче-
Решить задачу З можно было и без
использования ![]() формулы (5.6). Пусть отметка ученика нам
неизвестна и мы хотим ее определить, задавая ему вопросы, подразумевающие ответ
«да» или «нет». Сначала разумно спросить, не получил ли ученик отметку «4».
Если это не так, то далее имеет смысл спросить про «пятерку» . В случае неудачи
последним третьим вопросом мы уточним, оказался ли ученик аттестованным вообще.
Порядок вопросов здесь не случаен. Фактически мы определяем подмножество, к
которому принадлежит ученик согласно своей отметке (всего таких подмножеств 4).
После получения ответа на каждый следующий вопрос количество учащихся, среди
которых может находиться наш ученик, уменьшается в два раза, что соответствует
получению одного бита информации.
формулы (5.6). Пусть отметка ученика нам
неизвестна и мы хотим ее определить, задавая ему вопросы, подразумевающие ответ
«да» или «нет». Сначала разумно спросить, не получил ли ученик отметку «4».
Если это не так, то далее имеет смысл спросить про «пятерку» . В случае неудачи
последним третьим вопросом мы уточним, оказался ли ученик аттестованным вообще.
Порядок вопросов здесь не случаен. Фактически мы определяем подмножество, к
которому принадлежит ученик согласно своей отметке (всего таких подмножеств 4).
После получения ответа на каждый следующий вопрос количество учащихся, среди
которых может находиться наш ученик, уменьшается в два раза, что соответствует
получению одного бита информации.
Пример 7. Зная приблизительные частоты, с которыми встречаются буквы русского алфавита (в таблице ниже приведены средние округленные частоты употребления букв русского языка и символа «пробел» на каждую тысячу символов текста на русском языке), можно более точно, чем при использовании алфавитного подхода, не учитывающего вероятности появления различных символов, ответить на вопрос, сколько информации несет то или иное слово, например ваша фамилия.
|
Б ква |
п обел |
о |
е ё |
а |
и |
т |
н |
с |
|
в .л |
к |
м |
|
п |
|
|
|
Частота |
175 |
90 |
72 |
62 |
62 |
53 |
53 |
54 |
40 |
38 |
35 |
28 |
26 |
25 |
23 |
21 |
|
Б ква Частота |
я 18 |
16 |
16 |
14 |
14 |
13 |
12 |
10 |
9 |
7 |
6 |
6 |
4 |
з |
з |
2 |
Можно предложить другой подход к измерению информации, если отдельно кодировать корень фамилии, а отдельно ее окончание. Тогда можно обойтись и меньшим количеством бит. Так, окончание «ов» встречается как минимум в половине мужских фамилий россиян, т. е. несет всего один бит информации. Корень «Бел» встречается, предположим, один раз на 128 фамилий. То есть для его кодирования достаточно 7 бит. Тогда общий код для фамилии Белов теоретически может занимать всего один байт!
Наконец, можно просто узнать, как часто встречается фамилия Белов среди российских фамилий, и подсчитать ее информационный вес. Если предложенные выше цифры относительно частоты употребления в фамилиях корня «Бел» и окончания «ов» верны, то информационный вес фамилии в целом заключен между 7 и 8 битами.
Пример 8. В игре «Поле чудес» иногда разрешается открыть произвольную букву слова. Какую позицию следует выбрать? Считается, что искомое слово содержится в имеющемся у нас словаре.

Выберем из словаря все слова, состоящие
из того же числа букв, что и отгадываемое слово, и у которых на ![]() местах уже
разгаданных нами ранее букв стоят те же буквы. Для каждой из неоткрытых позиций
подсчитаем энтропию распределения частот появления в этой позиции различных
букв. Тогда открывать следует букву в той позиции, энтропия которой
максимальна.
местах уже
разгаданных нами ранее букв стоят те же буквы. Для каждой из неоткрытых позиций
подсчитаем энтропию распределения частот появления в этой позиции различных
букв. Тогда открывать следует букву в той позиции, энтропия которой
максимальна.
Вопросы и задания
1.
2. При игре в кости используют 2 одинаковых кубика, грани которых помечены числами от 1 до 6. Сколько информации несет сообщение о том, что при бросании двух кубиков в сумме выпало 4 очка?
З. В урне находятся 8 белых и 24 черных шара. Какое количество информации несет сообщение о том, что из урны достали белый шар? А черный шар?
4. Сообщение о том, что найден цветок сирени с 5 лепестками, несет 7 бит информации. Как часто встречаются подобные цветы на ветках сирени?
5. Для ремонта школы использовали белую, синюю и желтую краски. Израсходовали одинаковое количество белой и синей краски. Сообщение о том, что закончилась банка белой краски, несет 2 бита информации. Синей краски израсходовали 8 банок. Сколько банок желтой краски израсходовали на ремонт школы?
6. Постройте график функции Нф) = log21/p на интервале (О, 1]. Какие выводы можно сделать при исследовании этого графика?
7. В упражнении 6
из S 5.4 был описан словарь языка некое![]() го племени. Сколько информации на самом
деле несет
го племени. Сколько информации на самом
деле несет ![]() этот словарь, если 16 букв, с помощью
которых записаны все слова этого племени, встречаются в словаре со следующими
частотными характеристиками: 1/4, 1/8, 1/16, 1/32, 1/32, 1/8, 1/32, 1/16, 1/64,
1/64, 1/16, 1/16, 1/32, 1/32, 1/32, 1/32?
этот словарь, если 16 букв, с помощью
которых записаны все слова этого племени, встречаются в словаре со следующими
частотными характеристиками: 1/4, 1/8, 1/16, 1/32, 1/32, 1/8, 1/32, 1/16, 1/64,
1/64, 1/16, 1/16, 1/32, 1/32, 1/32, 1/32?
S 5.6. Оптимальное кодирование информации и ее сложность
Одной из важнейших задач современной информатики, как уже было показано в главе 2, является кодирование информации наиболее коротким образом.
Отметим, что если исследовать каждый
файл в отдельности, то в каждом конкретном случае более экономный способ
кодирования придумать можно, например алгоритм RLE (см. главу 2). При этом на
сегодняшний день разработаны универсальные способы ![]() кодирования информации,
например, алгоритм Хаффмана или арифметического кодирования, которые для
произвольного файла строят код, близкий к оптимальной оценке Шеннона.
кодирования информации,
например, алгоритм Хаффмана или арифметического кодирования, которые для
произвольного файла строят код, близкий к оптимальной оценке Шеннона.
Рассмотрим идею построения одного из универсальных алгоритмов кодирования. Так как различные символы встречаются в тексте с различной частотой, то естественно кодировать их так, чтобы те, которые встречаются чаще, кодировались более коротко, а те, которые встречаются реже, кодировались длиннее. Но если мы имеем неравномерный код (разные символы закодированы последовательностями разной длины), то возникает проблема: как понять, где кончился код одного символа и начался код другого? Эту проблему можно решать двумя способами: 1) закодированная последовательность имеет вид {длина кода, код}{длина кода, код}...{длина кода, код). Так устроены, например, коды Rice и Дельта-коды;
2) можно построить так называемый префиксный код: в нем не требуется указывать длину кода, но коды получаются несколько длинее.
Напомним, что код называется префиксным, если код одного символа не может быть началом кода другого символа.
В данном случае предложенный код О, 10, 110, 111 является префиксным. Более того, для любого четырехсимвольного алфавита с частотами встречаемости 1/2, 1/4, 1/8, 1/8 рассмотренный способ кодирования является оптимальным, так как каждый символ кодируется двоичной последовательностью длины, совпадающей с информационным весом каждого символа в отдельности. То есть в данном случае достигнута нижняя теоретическая граница сжатия.
Префиксный код Хаффмана
Для произвольного алфавита одним из
наиболее применимых алгоритмов построения префиксного кода, близкого к
оптимальному, является уже известный вам алгоритм Хаффмана. Докажем, что код, построенный
с его помощью, является префиксным. ![]()
Приведем конструктивное доказательство.
Если текст содержит всего два символа, то один из них кодируется нулем, а
второй — единицей. Предположим, что для алфавита, состоящего из N символов, код
Хаффмана уже построен. Рассмотрим алфавит, состоящий из лт + 1 сим![]() волов. Отождествим два наиболее редко встречающихся символа этого алфавита и
построим код Хаффмана для получившегося Л(-символьного алфавита. Если 6162 ...Ь
волов. Отождествим два наиболее редко встречающихся символа этого алфавита и
построим код Хаффмана для получившегося Л(-символьного алфавита. Если 6162 ...Ь
![]() код Хаффмана для «склеенного» символа,
то, не изменяя кодов остальных символов, определим коды «слипшихся» символов
как b1b2...bkO и b1b2...b 1. Так как последовательность 6162 ...Ьк не является
началом никакого другого кода символа нашего алфавита, то построенный код
является префиксным.
код Хаффмана для «склеенного» символа,
то, не изменяя кодов остальных символов, определим коды «слипшихся» символов
как b1b2...bkO и b1b2...b 1. Так как последовательность 6162 ...Ьк не является
началом никакого другого кода символа нашего алфавита, то построенный код
является префиксным.
![]()
Коэффициент сжатия информации может быть существенно увеличен за счет учета зависимости появления следующего символа в слове. Так, например, вероятность появления согласной буквы в текущей позиции существенно возрастает, если на предыдущей позиции стоит гласная буква. Новая идея посимвольного кодирования заключается в следующем: для каждого символа алфавита мы вычисляем распределение символов, непосредственно за ним следующих. И для каждого такого распределения мы построим свой код Хаффмана.
Другой способ сжатия файлов основан на анализе сложности содержащейся в них информации. Так, по-
![]()
следовательность 01010101010101 является менее сложной, чем 1001110000, так как первую из них можно заменить на более короткую, но построенную по другим правилам: 7(01) 1112(01), а пути сокращения второй последовательности не очевидны. Идея анализа сложности кодируемой информации лежит в основе алгоритмов RLE, Ш (см. главу 2).
Формальное понятие сложности введено, в частности, А. Н. Колмогоровым.
Определение 10. Сложность объекта ИЛИ явления (по Колмогорову) это минимальное число двоичных знаков (например, нулей и единиц), последовательностью которых можно описать (закодировать) всю информацию об объекте (явлении), достаточное для его дальнейшего воспроизведения (декодирования).
Пример 11. Является ли число п = 3,14159256... сложным? Как ни странно, нет. Для этого числа существует простое описание:
п = Длина любой окружности/ее Диаметр.
В этом сообщении, которое можно закодировать
и с помощью двоичного кода, содержится информация сразу ![]() обо всех цифрах
этого числа, что невозможно осуществить путем их последовательного выписывания.
обо всех цифрах
этого числа, что невозможно осуществить путем их последовательного выписывания.
Вопрос, Можно ли опреДелить, что построенный код для конкретной послеДовательности — минимальный?
Вопросы и задания ![]()
1. Является ли азбука Морзе примером префиксного кода?
2. Четырехсимвольный алфавит имеет следующее частотное распределение: 0,1; 0,2; 0,3; 0,4. Постройте код Хаффмана для записи сообщений с помощью этого алфавита.
З. Постройте код Хаффмана для 16-буквенного алфавита с частотными характеристиками, указанными в задании 7 предыдущего параграфа. Подсчитав энтропию данного распределения, ответьте на вопрос, является ли полученный код оптимальным.
4. В S 5.6 говорится, что если длина файла невелика, а символы встречаются примерно с одинаковой частотой, то кодирование по Хаффману не приведет к сжатию файла. А для файлов большого размера с существенно различными частотными характеристиками символов выигрыш может быть значительным. Подтвердите (или опровергните) данное высказывание численным моделированием .
5. Напишите программу, позволяющую кодировать и декодировать по Хаффману файлы с известными частотными характеристиками. Сравните работу вашей программы с результатами сжатия тех же файлов с помощью стандартных архиваторов. Назовите преимущества и недостатки оптимального префиксного кода.
Заключение
В этой главе вы познакомились с основами математической теории информации. Узнали несколько согласованных подходов к измерению количества информации. Формулы Хартли и Шеннона, изученные в данной главе, помогут вам правильно вычислять количество информации в различных случаях. Надеемся, что вы сможете применять их на практике во всевозможных жизненных ситуациях.
Одним из наиболее значимых применений математической теории информации является создание способов записи информации, близких к оптимальному кодированию, о котором было рассказано в материалах учебника. Кодирование по Хаффману, изученное вами, демонстрирует один из таких способов.
![]() Если данная тема вас заинтересовала, то в
материалах учебника можно найти немало проблем, требующих более детального
исследования с помощью методов мате
Если данная тема вас заинтересовала, то в
материалах учебника можно найти немало проблем, требующих более детального
исследования с помощью методов мате![]() матической теории информации. Попробуйте
придумать оптимальные стратегии поведения в тех или иных телевизионных играх
или постарайтесь изобрести свой собственный способ сжатия информации,
запрограммируйте его и сравните с известными программами-архиваторами. Творите,
и у вас все получится!
матической теории информации. Попробуйте
придумать оптимальные стратегии поведения в тех или иных телевизионных играх
или постарайтесь изобрести свой собственный способ сжатия информации,
запрограммируйте его и сравните с известными программами-архиваторами. Творите,
и у вас все получится!
Глава 6
![]()
Математические основы вычислительной геометрии
и компьютерной графики
![]()
Геометрия есть искусство правильно рассуждать на неправильных чертежах.
Д. Пойа
С тех пор, как Евклид написал свои «Элементы геометрии» , не нашлось никого, кто бы их отверг... В этих «Элементах...» содержится непреложная истина, с которой разум, раз познав ее, не может не согласиться.
П. ГассенДи
S 6.1. Координаты и векторы на плоскости
S 6.2. Способы описания
линий на плоскости ![]()
S 6.3. Задачи компьютерной графики на взаимное расположение точек и фигур
S 6.4. Многоугольники
S 6.5. Геометрические объекты в пространстве
гда вы играете в компьютерные игры,
смотрите рекламные ролики или становитесь свидетелями гибели «Титаника» на
экране кинематографа, то невольно погружаетесь в волшебный мир компьютерной
графики. Задачи компьютерной графики возникли относительно недавно — в середине
80-х годов прошлого столетия вместе с появлением графических дисплеев.
Параллельно с совершенствованием аппаратных средств росла и сложность
математических задач, решение которых становилось при этом возможным. Настоящую
революцию среди 0-игр (от английского 3-dimensional) произвел Тот. Его так
называемый «движок» получил широкое распространение среди разработчиков компью![]() терных игр, т. е. «стал властителем дум» О. При создании подобных шедевров
компьютерной графики должны сойтись воедино мастерство художника, искусство
программиста и знания математика.
терных игр, т. е. «стал властителем дум» О. При создании подобных шедевров
компьютерной графики должны сойтись воедино мастерство художника, искусство
программиста и знания математика.
Раздел информатики, изучающий алгоритмы решения задач аналитической геометрии, называется ВЫЧислительной геометрией. Одной из ее задач является получение аналитических формул и алгоритмов обработки геометрических фигур в виде, удобном именно для компьютерной реализации. Как «не все йогурты одинаково полезны», так и не всякое математическое описание геометрических объектов может быть при этом использовано.
Задачи аналитического описания геометрических объектов возникают не только в компьютерной графике, но и при проектировании интегральных схем, технических устройств и др. Иметь дело с геометрией приходится и мэру любого города. Ведь перед ним может встать любая из следующих задач: как разделить город на районы примерно равной площади и с одинаковым числом жителей, где построить новый культурный центр, а где — химический завод и т. д. и т. п. Ответы на эти и многие другие вопросы тоже может дать вычислительная геометрия.
Исходными данными в задачах подобного рода могут быть множество точек, набор отрезков или многоугольников и т. п. Результатом является либо ответ на какой-то вопрос (типа «пересекаются ли проекции этих объектов»; подобная проблема постоянно возникает как раз при программировании компьютерных игр), либо какой-то геометрический объект (например, наименьший выпуклый многоугольник, содержащий заданные точки; на практике эта задача может соответствовать проектированию кольцевой дороги вокруг населенного пункта).
S 6.1 . Координаты и векторы на плоскости
Для того чтобы геометрические образы перевести на язык формул, в первую очередь необходимо ввести систему координат (СК). В аналитической геометрии используются различные СК на плоскости и в пространстве, но мы будем работать с прямоугольной декартовой СК. Общепринято выбирать координатные оси так, чтобы поворот на угол п/2, при котором ось Ох совмещается с осью Оу, происходил против часовой стрелки. Такую СК называют правой. В дальнейшем подразумевается, что наша СК правая. В такой СК направление поворота против часовой стрелки называется положительным.
Теперь с каждой точкой на плоскости будут связаны два числа координаты этой точки в данной СК, и геометрические объекты могут получить аналитическое выражение. Так, чтобы задать отрезок, достаточно указать координаты его концов. Прямую можно задать, указав пару ее точек, либо координатами одной ее точки и век-
тором, характеризующим направление этой
прямой и т. д. Основным инструментом при решении задач для ![]() нас будут
векторы. Напомним некоторые сведения о них.
нас будут
векторы. Напомним некоторые сведения о них.
Определение 1. Отрезок АВ, у которого точку А считают началом (точкой приложения), а точку В — КОНЦоМ, называют вектором АВ и обозначают либо АВ, либо жирной строчной латинской буквой, например а. Для обозначения длины вектора (т. е. длины соответствующего отрезка) будем пользоваться символом модуля (например, Д). Два вектора называются равными, если они совмещаются параллельным переносом.
Пусть точки А и В имеют координаты (хр Щ) и (ху у»
![]() соответственно. Координатами вектора АВ называется пара
чисел (х2 — хр — Щ). Наоборот, если вектор а имеет координаты (а , а ) и
приложен к точке (хр У1), то легко вычислить координаты (ху У2) его конца:
соответственно. Координатами вектора АВ называется пара
чисел (х2 — хр — Щ). Наоборот, если вектор а имеет координаты (а , а ) и
приложен к точке (хр У1), то легко вычислить координаты (ху У2) его конца:
.х2 = х 1 + ах, У2 = + а ![]()
![]()
![]()
ах![]()
Любая упорядоченная пара чисел (х, у) может также рассматриваться как вектор. Геометрически вектор — это направленный отрезок, начинающийся в точке (0, О) и заканчивающийся в точке (х, у). Вектор, заданный двумя своими координатами (х, у), называют свободным вектором. Всем векторам, заданным координатами начала и конца и равным между собой, соответствует один и тот же свободный вектор. Для такого вектора не определена точка приложения.
Векторы можно складывать и умножать на
числа. Сложение векторов производится по правилу треуголь![]() ника или по правилу
параллелограмма (рис. 6.1). Под разностью векторов а и Ь понимают сумму вектора
а и вектора, противоположного вектору Ь (т. е. совпадающего с ним по длине, но
противоположно направленного). При умножении вектора а на число t получается
ника или по правилу
параллелограмма (рис. 6.1). Под разностью векторов а и Ь понимают сумму вектора
а и вектора, противоположного вектору Ь (т. е. совпадающего с ним по длине, но
противоположно направленного). При умножении вектора а на число t получается
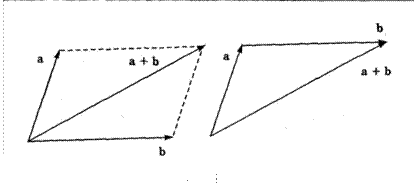
вектор, имеющий длину ltHai•, его направление совпадает с направлением а, если t > О, и противоположно ему, если t < О.
Операция умножения вектора на числовую константу дает возможность ввести понятие коллинеарности и неколлинеарности векторов.
Определение 2. Два вектора а и Ь называются коллинеарными (сонаправленными или противоположно направленными), если хотя бы один из них может быть выражен через другой в виде формулы Ь = t•a. При этом будем
считать, что ![]() а
а
Выразим введенные операции над векторами
через их координаты. Если если а = (ах, а ) и Ь = (Ьх, Ьу), ТО а + Ь = (ах +
ьх, ау + Ь а — Ь = (ах Ьх, ау ![]() и = (t•ax, ).
и = (t•ax, ).
Отметим еще, что вектор, сонаправленный с данным вектором а и имеющий заданную длину l, можно выразить следующим образом: — а. В дальнейшем мы неода нократно будем этим пользоваться.
Вопрос. Пусть нам известно, что АВ/АС < 0. Что вы можете сказать о взаимном расположении точек А, В и С?
Ответ. Из цруведенного выше неравенства следует, что векторы АВ и АС коллинеарны и АВ = t • АС, где t < О. Это означает, что точки А, В и С лежат на одной прямой, и векторы АВ и АС отложены от одной точки А в противоположных направлениях. Следовательно, точка А лежит между В и С.
Определение З. Скалярным произведением
двух ненулевых векторов а = (а , а ) и Ь (Ь Ь ) называется число (а, Ь) ![]() =
= ![]() (Р,
где (Р — угол между этими векторами. В координатах оно вычисляется так: (а, Ь)
= а Ь + а Ь
(Р,
где (Р — угол между этими векторами. В координатах оно вычисляется так: (а, Ь)
= а Ь + а Ь ![]()
Вопрос. Как можно использовать скалярное произвеДение для характеристики угла между векторами?
Ответ. Из приведенных в определении З
формул следует, что два ненулевых вектора перпендикулярны тогда и только тогда,
когда их скалярное произведение равно нулю (cos л/2 = О). Так как cos (Р
положителен для острых углов и отрицателен для тупых, угол между векторами
острый (тупой) в том и только том случае, когда их ска![]() лярное произведение
положительно (отрицательно). П
лярное произведение
положительно (отрицательно). П
Пусть а и Ь — два ненулевых вектора, отложенные от одной точки. В школьном курсе геометрии под углом между векторами понимается меньший из двух углов между лучами, на которых лежат векторы а и Ь. Значение такого угла всегда находится в промежутке [О; п].
В связи с этим говорят также, что пара
векторов а и Ь ![]() положительно (отрицательно) ориентирована.
Ориентированный угол может принимать значения от —л до п. На рис. б.?_ориентированные
углы, нацруме№_ между векторами ОА и ОВ и между векторами ОВ и ОА
равны по модулю, но первый из них отрицательный, а второй — положительный.
положительно (отрицательно) ориентирована.
Ориентированный угол может принимать значения от —л до п. На рис. б.?_ориентированные
углы, нацруме№_ между векторами ОА и ОВ и между векторами ОВ и ОА
равны по модулю, но первый из них отрицательный, а второй — положительный.
Вопрос. Как, зная коорДинаты векторов, найти угол межДу ними?
Ответ. Очевидный способ следует из
формулы для скалярного произведения: cos (Р = (а, ![]() Однако при этом
получится значение неориентированного угла и часть
Однако при этом
получится значение неориентированного угла и часть
Рис. 6.2
информации (возможно, полезная) будет нами потеряна. Кроме того, использование этой формулы для программирования не всегда удобно. Например, в языке Паскаль, как и в ряде других языков программирования, из обратных тригонометрических функций реализована только функция arctg (Р. Мы покажем, как найти угол иначе, после того как познакомимся с ориентированной площадью треугольника.
Ориентированная площадь треугольника
это его обычная площадь, снабженная знаком. Знак у ориенти![]() рованной
площади треугольника АВС такой же, как у ориентированного угла
между векторами АВ и АС. То есть ее знак зависит от порядка перечисления
вершин. Если вершины треугольника перечисляются против часовой стрелки,
ориентированная площадь положительна, а если по часовой стрелке отрицательна.
На рис. 6.2 треугольник АВС — прямоугольный. Его ориентированная площадь равна
рованной
площади треугольника АВС такой же, как у ориентированного угла
между векторами АВ и АС. То есть ее знак зависит от порядка перечисления
вершин. Если вершины треугольника перечисляются против часовой стрелки,
ориентированная площадь положительна, а если по часовой стрелке отрицательна.
На рис. 6.2 треугольник АВС — прямоугольный. Его ориентированная площадь равна ![]() Эту
же величину можно вычислить другим способом. Пусть О — произвольная точка
плоскости. На нашем рисунке площадь треугольника АВС получится, если из площади
треугольника ОВС вычесть площадь треугольника ОАВ и прибавить площадь
треугольника ОСА. Таким образом, нужно просто сложить ориентированные площади
треугольников ОАВ, ОВС и ОСА. Это правило работает при любом выборе точки О.
Эту
же величину можно вычислить другим способом. Пусть О — произвольная точка
плоскости. На нашем рисунке площадь треугольника АВС получится, если из площади
треугольника ОВС вычесть площадь треугольника ОАВ и прибавить площадь
треугольника ОСА. Таким образом, нужно просто сложить ориентированные площади
треугольников ОАВ, ОВС и ОСА. Это правило работает при любом выборе точки О.
Посмотрим, как выразить ориентированную
площадь треугольника в координатах. Пусть S — ориентированная площадь
треугольника ОАВ, построенного на векторах а = (а , а ) и Ь = (Ь Ь Вычислим ее
для конкретного расположения векторов (рис. 6.3). Величина S
здесь положительна (пара векторов ОА и ОВ положительно ориентирована). Достроим
наш треугольник до параллелограмма ОАСВ площади 2S (здесь
ОС![]()
![]() ОА + ОВ). Тогда площадь прямоугольника ОС1СС2 равна
ОА + ОВ). Тогда площадь прямоугольника ОС1СС2 равна ![]() =
(ах + + Ь ). Вместе с тем ее можно выразить так: 2S + 2S1 + 4S2 +У 2S3
= 2S + а а + Ь Ь + 2b а (здесь S1, S2, S3 — обычные неориентированные площади).
Раскрыв скобки в первом выражении для площади прямоугольника и выразив 2S из
равенства двух представлений, получим:
=
(ах + + Ь ). Вместе с тем ее можно выразить так: 2S + 2S1 + 4S2 +У 2S3
= 2S + а а + Ь Ь + 2b а (здесь S1, S2, S3 — обычные неориентированные площади).
Раскрыв скобки в первом выражении для площади прямоугольника и выразив 2S из
равенства двух представлений, получим:
![]() — Ьхау. (6.1)
— Ьхау. (6.1)
Рис. 6 З
Определение 4. Величина а Ь — Ь а называется косым (или псевдоскалярным) произвеДением векторов а и Ь.
Для косого произведения мы будем
употреблять обозначение [а, Ь]. Заметим, что в дальнейшем при определении
операций над векторами в пространстве мы будем использовать это же обозначение
в несколько другом смысле. Название рассматриваемой здесь величины связано со
свойством косой симметрии: [а, Ь] —![]()
![]() Так как неориентированная площадь параллелограмма, построенного
на векторах а и Ь, равна lablbb sind, а знак sin совпадает со знаком
ориентированного угла (Р, то [а, Ь] = lal• bbsinp. Величина [а, Ь] больше нуля,
если пара векторов а и Ь положительно ориентирована и меньше нуля в противном
случае. Косое произведение ненулевых векторов равно нулю тогда и только тогда,
когда они коллинеарны (sin О = sin п = О).
Так как неориентированная площадь параллелограмма, построенного
на векторах а и Ь, равна lablbb sind, а знак sin совпадает со знаком
ориентированного угла (Р, то [а, Ь] = lal• bbsinp. Величина [а, Ь] больше нуля,
если пара векторов а и Ь положительно ориентирована и меньше нуля в противном
случае. Косое произведение ненулевых векторов равно нулю тогда и только тогда,
когда они коллинеарны (sin О = sin п = О).
= (Ь , Ь ). Сопоставляя формулы для скалярного и косого произведения этих векторов, имеем
tgp = [а, Ь) (ару
![]()
Зная тангенс угла между векторами, мы
легко найдем угол между прямыми, на которых лежат а и Ь: он равен arctg([a, ![]() Чтобы
получить ориентированный угол между векторами, осталось выяснить, острый он или
тупой. Это мы определим по знаку скалярного произведения. Учтем еще, что знак
ориентированного угла совпадает со знаком косого произведения. Тогда
окончательно имеем:
Чтобы
получить ориентированный угол между векторами, осталось выяснить, острый он или
тупой. Это мы определим по знаку скалярного произведения. Учтем еще, что знак
ориентированного угла совпадает со знаком косого произведения. Тогда
окончательно имеем:
![]() п/2, если
(а, Ь) = О, [а, Ь] > О; —п/2, если (а, Ь) = О, [а, Ь] < О;
arctg([a,
п/2, если
(а, Ь) = О, [а, Ь] > О; —п/2, если (а, Ь) = О, [а, Ь] < О;
arctg([a, ![]() Ь)), если (а, Ь) > О; (6.2) arctg([a,
Ь)), если (а, Ь) > О; (6.2) arctg([a, ![]() Ь)) + п, если (а, Ь) < О, [а, Ь] О;
arctg([a,
Ь)) + п, если (а, Ь) < О, [а, Ь] О;
arctg([a, ![]() Ь)) — п, если (а, Ь) < О, [а, Ь] < О.
Ь)) — п, если (а, Ь) < О, [а, Ь] < О.
Величина обычного угла равна модулю значения ориентированного угла.
Отметим, что все сказанное об ориентированных углах и площадях относилось к правой СК. Может статься, что для конкретной задачи удобнее ввести левую СК. К примеру, координаты пикселей на экране монитора даются именно в левой СК (ось абсцисс смотрит вправо, ось ординат — вниз). При таком выборе осей положительным является поворот по часовой стрелке. С этой поправкой все вышеизложенное применимо и к левой СК.
Вопросы и задания
1. С
какими новыми понятиями, не известными вам из курса геометрии, вы познакомились
при изучении данного ![]() параграфа?
параграфа?
2. Выпишите формулы, аналогичные (6.2), для определения неориентированного угла между двумя векторами, значение которого лежит в диапазоне [О; п].
а) все три точки совпадают;
б) совпадают ровно две точки;
в) три точки различны и лежат на одной прямой;
![]() г) три точки образуют прямоугольный
треугольник;
г) три точки образуют прямоугольный
треугольник;
д) три точки образуют остроугольный треугольник;
е) три точки образуют тупоугольный треугольник.
S 6,2, Способы описания линий на плоскости
6.2.1. Общее уравнение прямой
В школьной математике для описания прямой на плоскости используется формула у = Кх + Ь, где К = tg ос, Ь = у(О).
Здесь ос — угол наклона описываемой прямой к оси Ох. Этот способ описания называется формулой с угловым коэффициентом. Она проста и понятна, однако не описывает прямые, параллельные оси Оу. Данный случай можно было бы учитывать отдельно, но при программировании это очень неудобно. Поэтому выведем общее уравнение прямой, используемое в аналитической геометрии.
Пусть на прямой заданы две несовпадающие точки: Р 1 с координатами (хр У1) и Р 2 с координатами (ху у».
Соответственно вектор с началом в точке Р 1 и концом в точке Р 2 имеет координаты (х2 — хр — У1). Если Р(х, у) — произвольная точка на нашей прямой, то координаты вектора ЦР равны (х — Ч, у — Щ). С помощью косого произведения условие коллинеарности векторов РIР
![]()
и Р1Р2 можно выразить так:
![]()
[Ц Р, РIР2] = (х — — У1) — (у — — х1) = О, или
(У2 — У1)х + (х1 — Х2)у + Х1(У1 — у» + У1(Х2 — хр = 0. (6.3)
Второе из уравнений (6.3) перепишем следующим образом:
ах + бу + с = О,
![]() При программировании первую из формул (6.3) нельзя
использовать в форме отношения (х2
При программировании первую из формул (6.3) нельзя
использовать в форме отношения (х2 ![]()
— (У2 — — Щ), так как, во-первых, даже если все координаты заданных точек целые, как это бывает в компьютерной графике, особенности реализации операции деления в вещественной арифметике не позволят с помощью указанного соотношения проверить принадлежность той или иной точки данной прямой, во-вторых, если точка Р совпадет с Р 1 , программа будет прервана в силу деления на ноль.
Определение 5. Любой ненулевой вектор, ортогональный прямой (т. е. ортогональный направляющему вектору прямой), называется нормалью к этой прямой.
Пусть заданная точка Ро прямой имеет
координаты (хо, уо), а некоторый вектор нормали п к ней — координаты (а, Ь).
Если Р(х, у) — произвольная точка на нашей ![]() прямой, то
координаты вектора РОР равны (х — хо, у — уо). Теперь скалярное
произведение ортогональных векторов (п, РоР) можно выразить так:
прямой, то
координаты вектора РОР равны (х — хо, у — уо). Теперь скалярное
произведение ортогональных векторов (п, РоР) можно выразить так:
(п, РоР) = а(х — хо) + Цу — уо) = О.
Очевидно, что уравнение (6.5) также
несложно привести к виду (6.4). Тогда становится понятно, что коэффици![]() енты
а и Ь из уравнения (6.4) представляют собой координаты одного из векторов
нормали к описываемой данным уравнением прямой. Отсюда следует, что при любых
значениях коэффициентов а, Ь и с (кроме а = Ь = О) уравне
енты
а и Ь из уравнения (6.4) представляют собой координаты одного из векторов
нормали к описываемой данным уравнением прямой. Отсюда следует, что при любых
значениях коэффициентов а, Ь и с (кроме а = Ь = О) уравне![]() ние (6.4) задает
прямую. Ею будет прямая, перпендикулярная вектору (а, Ь) и проходящая через
точку, чьи координаты удовлетворяют (6.4). При а О такой точкой будет,
например, точка (—с/а, О), при а = О точка
ние (6.4) задает
прямую. Ею будет прямая, перпендикулярная вектору (а, Ь) и проходящая через
точку, чьи координаты удовлетворяют (6.4). При а О такой точкой будет,
например, точка (—с/а, О), при а = О точка
![]()
![]()
6,2.2, Нормированное уравнение прямой
Через начало координат (точка О) проведем прямую, перпендикулярную нашей прямой L, точку их пересечения обозначим через М, длину отрезка ОМ обозначим через r (рис. 6.4). На построенной прямой возьмем вектор п единичной длины, направление которого совпадает с направлением ОМ (если наша прямая 1., проходит через начало координат, то можно выбрать любое из двух направлений).
Попробуем выразить общее уравнение нашей прямой через два параметра: r — длину вектора ОМ и угол 6 между вектором п и осью Ох. Для этого • воспользуемся двумя достаточно очевидными фактами.
1) Так как lnl = 1, то его координаты можно представить в виде п = (cos 9, sin 0).
2) Произвольная точка Р(х, у) принадлежит нашей прямой L тогда и только тогда, когда
![]() ОР)
= r.
ОР)
= r. ![]()
Тогда, с одной
стороны, ![]()
(п, ОР) = х cose + у sin Э, ![]() а с
другой стороны
а с
другой стороны
(п, ОР) = ![]() ОР) = r, так как Д —
ОР) = r, так как Д —![]()
Таким образом, х cos6 + у sine — или
х cos6 + у sin6 — r= О. (6.6)
Вычислить величины и е по общему уравнению прямой можно следующим образом.
1. Добьемся, чтобы коэффициент с в общем уравнении прямой был отрицательным. Если изначально это не так, умножим исходное уравнение на —1.
2.
Разделим все члены
уравнения на величину а2 + Ь2 ![]()
Тем самым получим:
Здесь 
6.2.3. Параметрические уравнения прямой, луча,
отрезка
Уравнение прямой, проходящей через несовпадающие точки Р1(хр У1) и Р 4х2 , у», можно записывать и в параметрическом виде. Любой вектор, приложенный к точке Р 1 и заканчивающийся в произвольной точке Р(х, у), леэкащей на той же прямой, по определению 2 можно получить из РIР2 путем умножения на некоторое вещественное число t:
![]() 1 1 2 •
1 1 2 •
![]() 1 — t(X2
1 — t(X2![]()
Выразив отсюда х и у, получаем систему параметрических уравнений, которой удовлетворяют координаты каждой точки Р(х, у) нашей прямой:
![]()
Наоборот, если координаты (х, у) точки Р удовлетворяют соотношениям (6.7), вектор ЦР коллинеарен РIР2 и, значит, точка Р лежит на прямой Р 1 Р 2. Таким образом, система уравнений (6.7), где параметр t пробегает всю действительную ось, задает прямую Р 1 Р 2
![]()
Эта же система, но со введенными ограничениями на значения t, будет задавать и отрезок Р Р 2 , и луч Р 1 Р 2 , начинающийся в точке Р 1 и проходящий через точку Р 2 , не совпадающую с Р 1. Координата х отрезка Р 1 Р 2 меняется в диапазоне [х1; х2], а у — в диапазоне [ 91 1 ; У2]. Следовательно, t е [О; 1]. Для всех точек Р(х, у), принадлеэкащих лучу Р 1 Р 2 , вектор ЦР сонаправлен с вектором РIР2. То есть для луча t е [О; 00).
6.2.4. Способы описания окружности
Известно, что точка М(х, у) принадлежит окружности с центром в точке Мо(хо, уо) и радиусом тогда и только тогда, когда расстояние между Мо и М равно r. Записав формулу для вычисления квадрата расстояния между двумя точками, мы придем к следующему уравнению окружности:
(х
- хо) 2 + (у - уо) 2![]()
На практике оказывается полезным знание
также и параметрических уравнений окружности. Обратимся сначала к окружности с
центром в начале координат. Если обозначить как t угол между радиус-вектором ОМ
(здесь М(х, у) произвольная точка окружности) и осью Ох, отсчитываемый против
часовой стрелки, то очевидно, что ![]() х = rcos t, у = rsin t.
х = rcos t, у = rsin t.
х = хо + rcos t, у = уо + rsin t. (6.9)
Уравнения, аналогичные (6.9), используются для описания таких кривых, как циклоида, эпициклоида, гипоциклоида и многих других, широко применяемых в компьютерной графике для получения различных узоров (рис. 6.5). Именно с помощью параметрических уравнений достаточно просто запрограммировать рисование подобных кривых на графическом экране.
Рис. 6.5. Гипоциклоида и эпициклоида
Вопросы и задания
1. Исходя из геометрического смысла коэффициентов нормированного уравнения прямой (6.6), выведите уравнение прямой, параллельной данной и находящейся от нее на заданном расстоянии r.
2. Покажите, что выражение |X1cos 9 + Y1Sin Э — для произвольной точки плоскости (хр У1) обозначает расстояние от этой точки до прямой xcos 9 + ysin 9 — = О.
З. Используя (6.7), составьте и решите
систему линейных уравнений для нахождения точки пересечения двух прямых. С
помощью решения этой же системы сформулируйте, как можно определить,
пересекаются ли соответ![]() ствующие отрезки (лучи).
ствующие отрезки (лучи).
4. Найдите в справочной литературе параметрические уравнения циклоиды, эпициклоиды и гипоциклоиды. С помощью любого известного вам языка программирования или электронной таблицы получите изображения данных кривых. Исследуйте их при различных значениях параметров.
6.3, 1 .
Прямая, перпендикулярная данной ![]()
и проходящая через заданную точку
В компьютерной
графике часто возникает необходимость восстановить квадрат, стороны которого не
обязательно параллельны осям координат, по одной из его сторон. Для решения
этой задачи надо уметь строить ![]() прямую, перпендикулярную данной и
проходящую через заданную точку.
прямую, перпендикулярную данной и
проходящую через заданную точку.
Пусть заданная точка Ро искомой прямой имеет координаты (хо, уо). Если Р(х, у) — произвольная точка на той же прямой, то координаты вектора РОР равны (х — хо, у — уо). Этот вектор перпендикулярен вектору РIР2, где Р1(хр У1) и Р2(Х2, У2) — точки на исходной прямой. Тогда скалярное произведение ортогональных векторов (РIР2, РоР) можно выразить так:
![]() — хо) + (У2 — —
уо) = О или
— хо) + (У2 — —
уо) = О или
(х2 — Х1)х + (У2 — У1)у + (х1 — Х2)хо + (У1 — У2)уо = О. (6.10)
Если же исходная прямая задана коэффициентами а, Ь и с своего уравнения, то легко заметить, что вектор ее нормали с координатами (а, Ь) коллинеарен вектору РоР.
Тогда, записывая косое произведение этих векторов, получим:
Цх — хо) — а(у — уо) = О.
6.3.2. Расположение точки относительно прямой,
луча или отрезка
![]()
![]() Если прямая задана двумя своими точками, то для
определения расположения точки плоскости относительно этой прямой уравнение
прямой выписывать не нужно.
Если прямая задана двумя своими точками, то для
определения расположения точки плоскости относительно этой прямой уравнение
прямой выписывать не нужно.
В случае проверки принадлежности точки лучу при равенстве [РIР2, АР] нулю (здесь Р 1 начало луча, а Р 2 — любая точка, принадлежащая лучу) полезно вычислить и скалярное произведение этих же векторов. Если оно меньше нуля, то Р 1 лежит на прямой между Р 2 и Р, следовательно, Р лучу не принадлежит. Чтобы
зоо
![]()
в аналогичной ситуации убедиться в принадлежности точки Р отрезку Р 1Р2, необходимо вычислить еще и значение скалярного произведения (Р2Р1, Р2Р). Если оно не-
отрицательно, то точка Р лежит на отрезке.
Подобные задачи в компьютерной графике приходится решать для точки графического экрана и линий (отрезков), описывающих границы тех или иных объектов.
Вопрос. Как опреДелить, на каком расстоянии находится заданная точка Р от определенной прямой, луча или отрезка?
![]() Ответ, Формула для
расстояния от точки до прямой полу
Ответ, Формула для
расстояния от точки до прямой полу![]() чается из сопоставления двух способов
вычисления площади треугольника: S =
чается из сопоставления двух способов
вычисления площади треугольника: S = ![]() PP2]l (рис. 6.6).
То есть расстояние от точки Р до прямой, заданной координатами точек Р 1 и Р 2
, можно подсчитать как отношение модуля косого произведения
векторов РР1 и РР2 к длине отрезка Р 1Р2.
PP2]l (рис. 6.6).
То есть расстояние от точки Р до прямой, заданной координатами точек Р 1 и Р 2
, можно подсчитать как отношение модуля косого произведения
векторов РР1 и РР2 к длине отрезка Р 1Р2.
Рис. 6.6
Для луча или отрезка умазанный способ
нахождения расстояния нужно слегка подкорректировать. Точка Ро (рис. 6.6)
принадлежит лучу Р 1Р 2 в том и только том случае, когда скалярное
произведение (РIР2, Ц Р) О. Для отрезка Р 1Р 2 , конечно, нужно еще и
выполнение условия (Р2Р1, Р2Р) О. Тогда применима формула расстояния от точки
до прямой. В противном случае расстояние от точки до луча (отрезка) будет равно
расстоянию от точки до начала луча (до ближайшего конца отрезка).![]()
![]()
6,3.3. Взаимное расположение прямых, отрезков,
лучей
Данные задачи очень часто встречаются в компьютерной графике. В частности, при программировании компьютерных игр. Например, если требуется проанализировать, насколько удачно игрок произвел выстрел из того или иного оружия.
Легко выяснить, пересекаются ли две прямые или параллельны. Напомним еще раз, что условие коллинеарности двух векторов это равенство нулю их косого произведения. Если прямые заданы уравнениями а х + + b1Y + = О и чх + b2Y + c2 = О, то удобно перейти к их нормалям = (ар 61) и па = (Ч, 62). Тогда условие коллинеарности нормалей (а значит, и параллельности прямых): [Ч, п? ] = a1b2 — a2b1 = О. Если прямые заданы парами точек, то таким же способом проверяется коллинеарность направляющих векторов. Проверка наличия пересечения прямой и отрезка производится путем анализа взаимного расположения концов отрезка относительно прямой, как это было показано в п. 6.3.2.
Пусть прямая Щ х + b1Y + c1 = О и
отрезок пересекаются в одной точке. Найдем ее, предварительно выписав уравнение
прямой агх + b2Y + — О, проходящей через ![]() концы отрезка Р1(хр
У1) и Р4х2 , у». Для этого достаточно решить систему двух линейных уравнений,
каждое из которых представляет собой уравнение соответствующей прямой
относительно х и у:
концы отрезка Р1(хр
У1) и Р4х2 , у». Для этого достаточно решить систему двух линейных уравнений,
каждое из которых представляет собой уравнение соответствующей прямой
относительно х и у:
Х = (b1C2 ![]() а2Ь1);
а2Ь1);
(6.12)
у = (а2С1 ![]() a2b1).
a2b1).
Вопрос. Как проверить наличие пересечения двух отрезков?
Ответ. Проверить наличие пересечения двух отрезков (а в компьютерной графике
нас в основном интересует лишь сам факт пересечения) несложно опять же с
использованием косого произведения. Пусть первый отрезок задан ![]() точками Р 1
и Р2 , а второй — Рз и Р . Обозначим хтах1 и
точками Р 1
и Р2 , а второй — Рз и Р . Обозначим хтах1 и ![]() min1 — максимальную и
минимальную из первых координат первого отрезка, хтах2 min2 — то же для второго
отрезка. Для второй координаты аналогично имеем:
min1 — максимальную и
минимальную из первых координат первого отрезка, хтах2 min2 — то же для второго
отрезка. Для второй координаты аналогично имеем:
![]()
Упомянутые отрезки пересекаются тогда,
когда одно![]() временно выполняются следующие три
условия:
временно выполняются следующие три
условия:
1)
![]() пересекаются ограничивающие их прямоугольники, тах1 min2'
тах2 mtn1' У тах1 Ymin2 и Утах2 Ymin1'
пересекаются ограничивающие их прямоугольники, тах1 min2'
тах2 mtn1' У тах1 Ymin2 и Утах2 Ymin1' ![]()
2) косые произведения [РIРз, РIР2] и [РIР4, РIР2] имеют
![]()
разные знаки, точнее [РIРз, РIР2] • [РIР4, РIР2] О;
![]()
З) РзР4] •
[РзР2, РзР4] О.![]()
![]() Последние два условия
означают, что концы одного отрезка лежат по разные стороны от прямой, которой
принадлежит другой отрезок (см. п. 6.3.2). А первое условие исключает из
специального рассмотрения слу
Последние два условия
означают, что концы одного отрезка лежат по разные стороны от прямой, которой
принадлежит другой отрезок (см. п. 6.3.2). А первое условие исключает из
специального рассмотрения слу![]() чай равенства нулю всех четырех косых
произведений, при котором отрезки лежат на одной прямой и могут как
пересекаться, так и нет.
чай равенства нулю всех четырех косых
произведений, при котором отрезки лежат на одной прямой и могут как
пересекаться, так и нет.
Если же факт наличия пересечения нами
установлен, то для отрезков, находящихся на пересекающихся пря![]() мых, точка
пересечения ищется так же, как и в предыдущей задаче. Для отрезков одной прямой
их пересечение (точка или отрезок) ищется путем подсчета значения нескольких
скалярных произведений.
мых, точка
пересечения ищется так же, как и в предыдущей задаче. Для отрезков одной прямой
их пересечение (точка или отрезок) ищется путем подсчета значения нескольких
скалярных произведений.
Для проверки наличия пересечения двух
лучей Р 1Р 2 и ![]() РзР4 следует изучить взаимное
расположение соответствующих прямых. Равенство нулю косого произведения
[РIР2, РзР4] означает принадлежность лучей параллельным прямым.
Если эти прямые различны, то векторы РIРз и Р1Р2 неколлинеарны и, значит, косое
произведение [РIРз, РIР2] отлично от нуля. В этом случае лучи не пересекаются.
Когда лучи лежат на одной прямой, с помощью знака скалярного
произведения (РIР2, РзР4) можно понять, в одну или в разные стороны они
направлены. В первом случае скалярное произведение будет положительным, а во
втором отрицательным. Чтобы определить, какой из двух сонаправленных лучей
является их пересечением, можно подсчитать значение ска
РзР4 следует изучить взаимное
расположение соответствующих прямых. Равенство нулю косого произведения
[РIР2, РзР4] означает принадлежность лучей параллельным прямым.
Если эти прямые различны, то векторы РIРз и Р1Р2 неколлинеарны и, значит, косое
произведение [РIРз, РIР2] отлично от нуля. В этом случае лучи не пересекаются.
Когда лучи лежат на одной прямой, с помощью знака скалярного
произведения (РIР2, РзР4) можно понять, в одну или в разные стороны они
направлены. В первом случае скалярное произведение будет положительным, а во
втором отрицательным. Чтобы определить, какой из двух сонаправленных лучей
является их пересечением, можно подсчитать значение ска![]() лярного произведения (Р1Р2, Р1Рз). Если оно больше нуля, то пересечением
является луч РзР4, в противном случае луч Р? 2. В случае противоположной
направленности лучей их пересечение либо отрезок Р 1Р з, и тогда начало любого
из двух лучей лежит внутри дру-
лярного произведения (Р1Р2, Р1Рз). Если оно больше нуля, то пересечением
является луч РзР4, в противном случае луч Р? 2. В случае противоположной
направленности лучей их пересечение либо отрезок Р 1Р з, и тогда начало любого
из двух лучей лежит внутри дру-
зоз
![]()
гого луча: (Р1Р2, РIРз) > О, либо одна точка Р 1 = Рз: (Р1Р2, Р1Рз) = О, либо оно пусто: (РIР2, РIРз) < О.
Наконец, если прямые Р 1 Р 2 и РзР4 пересекаются в одной точке М: ([РIР2, РзР4] О), то найти эту точку можно так же, как в п. 6.3.2. Затем следует проверить, что М принадлежит каждому из лучей:
![]()
(РIР2, РIМ) О и (РзР4, РIМ) О.
6.3.4. Взаимное расположение окружности и прямой
Прямая может пересекать окружность в двух точках, касаться ее или не иметь с окружностью общих точек. Эти случаи легко определяются. Достаточно найти расстояние от центра окружности до данной прямой (по формуле расстояния от точки до прямой, см.
п. 6.3.2). Если это расстояние (обозначим его l) меньше радиуса окружности r, прямая пересекает окружность в двух точках, если равно ему, то прямая касается окружности, а если оно больше радиуса, то общих точек нет. В последнем случае нас может интересовать и расстояние от прямой до окружности. Оно равно I — т. Более сложной является задача поиска общих точек прямой и окружности.
Задача. Пусть окружность имеет центр в точке О(хо, уо) и раДиус r. Требуется найти уравнение касательных к ней, прохоДящих через точку Р1(Х1, И).
Решение. Здесь возможны три случая. Если l0P1l r, то Р 1 лежит внутри окружности, и касательных, проходящих через нее, не существует. Если l0P1| = r , то Р 1 лежит на окружности. Тогда у искомой касательной нам известны точка Р 1 и нормаль АО, и ее уравнение легко выписывается (см. п. 6.2.1). Наконец, в случае ОР 1 > точек касания две, и, обозначив одну из них Р 2 , мы имеем прямоугольный треугольник ОР2Р1 (рис. 6.7).
Мы будем искать координаты а = х2 — х 1 и Ь = — У1 вектора РIР2 . Длины сторон прямоугольного треугольни-
![]()
ка ОР2Р1 легко находятся. Выпишем скалярное
произведение векторов РIР2 и РIО: ![]()
(Р1Р2, 40) -- (Р = PIP2l 2 .
![]()
Рис. 6.7
Геометрический смысл косого произведения [Р1Р0 , РIР2] — удвоенная площадь треугольника РОР Р 1 , взятая со знаком «плюс» для одной из точек касания и с минусом — для другой:
![]()
ср, РIР2] = ± 0P2l•PlP2l.
Записывая эти же произведения в координатах, получим систему линейных уравнений относительно а и Ь: (хо — + (уо — = lPIP2l 2 ,
![]() (хо — — (уо — l0P21•lPIP21. (6.13)
(хо — — (уо — l0P21•lPIP21. (6.13)
Такую систему решить уже несложно. Далее по точке Р1(хр У1) и направляющему вектору РIР2 = (а, Ь) выписывается уравнение касательной. Задача решена. Если же нам требуется еще найти и координаты точки касания, то это можно сделать, используя координаты точки Р 1 и найденные координаты вектора РIР2.
К решению этой же задачи есть подход, при
котором не приходится решать даже систему линейных уравнений. Опустим из
вершины Р2 прямого угла высоту Р2Рз (см. рис. 6.7). Из подобия треугольников Р
1 Р 20 и Р1РзР2 найдем длины отрезков РIРз и РзР2: р 1 Р3' = iPIP2l 2 /10P1t;
|РзР2ј = ![]() Теперь последовательно находим
координаты вектора РIРз, точки Рз(хз, уз) и, наконец, используя известные
координаты вектора
Теперь последовательно находим
координаты вектора РIРз, точки Рз(хз, уз) и, наконец, используя известные
координаты вектора
![]()
п = (уо — Щ, х 1 — хо), перпендикулярного прямой Р 1 Р з, координаты точки Р2'. Р1Рз = Р1Рз • lPIP3|/lP101;
![]()
+ (РIРз)х, уз = + (Р1Р3)у; РзР2 = п.РзР2/п|;
![]()
= + (РзР2)х , = уз + (РзР2)у.
![]() Пусть теперь прямая
и окружность пересекаются в двух точках (рис. 6.8). Координаты этих точек можно
найти по следующему алгоритму. Найдем вектор п нормали к прямой. Отложим
в направлении этого вектора векто ОА длины l. Вычислим расстояние |AP11 = AP21
=
Пусть теперь прямая
и окружность пересекаются в двух точках (рис. 6.8). Координаты этих точек можно
найти по следующему алгоритму. Найдем вектор п нормали к прямой. Отложим
в направлении этого вектора векто ОА длины l. Вычислим расстояние |AP11 = AP21
= ![]() r2 — . От точки А вдоль прямой
отложим в обе стороны векторы длины ДР l. Их концы дадут нам две искомые точки
Р 1 и Р 2. Каждый из шагов этого алгоритма в отдельности нами уже
рассматривался ранее. Заметим только, что на первом шаге необходимо правильно
выбрать одно из двух возможных направлений нормали к прямой. Для этого достаточно
проверить, что скалярное произведение (п, ОМ) О, где М — произвольная точка
прямой.
r2 — . От точки А вдоль прямой
отложим в обе стороны векторы длины ДР l. Их концы дадут нам две искомые точки
Р 1 и Р 2. Каждый из шагов этого алгоритма в отдельности нами уже
рассматривался ранее. Заметим только, что на первом шаге необходимо правильно
выбрать одно из двух возможных направлений нормали к прямой. Для этого достаточно
проверить, что скалярное произведение (п, ОМ) О, где М — произвольная точка
прямой.
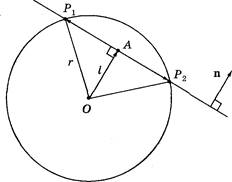
Рис. 6.8
6.3.5. Взаимное расположение двух окружностей
Две различные окружности также могут пересекаться в двух точках, касаться друг друга или не иметь общих точек. В последнем случае либо одна из окружностей располагается внутри другой (назовем такие окружности вложенными), либо каждая из окружностей лежит вне другой.
![]()
Проверка наличия пересечения или
касания аналогично предыдущей задаче осуществляется путем сравнения расстояния
между центрами окружностей (обозначим его l) и их радиусами. Если l>r + или
I < lr1 — r2l, то окружности общих точек не имеют. Второе условие как раз и
обозначает вложенность одной окруж![]() ности в другую. При замене знака любого
из этих двух неравенств на равенство мы получим случай касания окружностей
(внешнего или внутреннего). Если же
ности в другую. При замене знака любого
из этих двух неравенств на равенство мы получим случай касания окружностей
(внешнего или внутреннего). Если же ![]() — < < + П, то окружности имеют
ровно две точки пересечения.
— < < + П, то окружности имеют
ровно две точки пересечения.
![]() Координаты точки
касания окружностей найти очень просто. Ведь центры окружностей 01(х1, У1) и
04х2 , у 2) задают прямую, на которой лежит и точка касания Р(хз, уз). Будем
считать, что точка 01 является центром окружности большего
радиуса. Тогда вектор 01Р сонаправлен с вектором 0102 . Длины обоих векторов
также известны. Искомые координаты равны (х1 + (х2 — X1)r1/l, + + (У2 —
Y1)r1/l). Проверьте, что если < 7) , то в случае вложенности окружностей
полученная формула нуждается в корректировке.
Координаты точки
касания окружностей найти очень просто. Ведь центры окружностей 01(х1, У1) и
04х2 , у 2) задают прямую, на которой лежит и точка касания Р(хз, уз). Будем
считать, что точка 01 является центром окружности большего
радиуса. Тогда вектор 01Р сонаправлен с вектором 0102 . Длины обоих векторов
также известны. Искомые координаты равны (х1 + (х2 — X1)r1/l, + + (У2 —
Y1)r1/l). Проверьте, что если < 7) , то в случае вложенности окружностей
полученная формула нуждается в корректировке.
При поиске координат двух точек
пересечения окружностей воспользуемся механизмом, уже описанным в п. 6.3.4.
Рассмотрим треугольник 0102Р (рис. 6.9). В нем нам известны длины всех трех
сторон ![]() 1 > r,-z и l). Проведем в треугольнике
высоту РРо. В долучившемся прямоугольном треугольнике 01РОР неизвестны длины
катетов. Найдем 01 Ро, записав теорему косинусов для треугольника 0102Р:
1 > r,-z и l). Проведем в треугольнике
высоту РРо. В долучившемся прямоугольном треугольнике 01РОР неизвестны длины
катетов. Найдем 01 Ро, записав теорему косинусов для треугольника 0102Р:
![]() 2
2![]() 2 — 2lr1 cos = + l2
2 — 2lr1 cos = + l2![]()
Отсюда l01Pol = (К + [2 — К) / 2l. По теореме
Пифагора l popl = — . Теперь последовательно находим: ![]() вектор 01
Ро = 01Po|/l;
вектор 01
Ро = 01Po|/l;
![]()
![]() точку Ро по известной точке 01 и вектору
014;
точку Ро по известной точке 01 и вектору
014; ![]() вектор — ур х1 — х2), перпендикулярный
0102',
вектор — ур х1 — х2), перпендикулярный
0102',
![]() вектор РОР = lPoP| • n/lnl;
вектор РОР = lPoP| • n/lnl; ![]() наконец,
точку Р по известной точке Ро и вектору
наконец,
точку Р по известной точке Ро и вектору
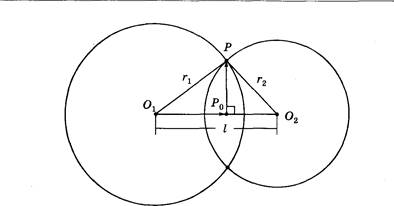
Рис. 6.9
Заменив в последнем действии вектор п на противоположный, получим и вторую точку пересечения окружностеЙ.
Вопросы и задания
1. Научитесь определять взаимное расположение двух точек относительно одной прямой.
2. Пусть известно, что два отрезка, заданные своими концами, лежат на одной прямой. По значениям каких скалярных произведений можно определить, пересекаются они или нет?
З. Решите систему линейных уравнений (6.13) для нахождения направляющего вектора касательной к окружности.
4. Пусть векторы РоР1 (хр У1) и РоР2 (хр У2) приложены к точке Ро(хо, уо). Найдите уравнение биссектрисы угла PlP0P2.
5. На плане местности болото обозначено окружностью, координаты центра которой и радиус известны. Составьте алгоритм нахождения длины кратчайшего пути между двумя точками плоскости, если болото непроходимо (обе точки находятся вне болота).
S 6,4. Многоугольники
Практически любой объект на графическом экране компьютера ![]() помощью
выпуклого или невыпуклого многоугольника. При анализе подобных объектов и
программировании их взаимодействия воз-
помощью
выпуклого или невыпуклого многоугольника. При анализе подобных объектов и
программировании их взаимодействия воз-
![]()
никает множество различных задач вычислительной геометрии. Рассмотрим наиболее важные из них.
6.4.1 . Проверка выпуклости многоугольника
Очевидно, что большинство задач вычислительной геометрии, связанных с многоугольниками, имеют более простое решение в случае их выпуклости. Поэтому сначала научимся проверять для многоугольника именно это свойство.
Выпуклость многоугольника с вершинами Р 1 , Р2 ,![]()
Р , перечисленными в порядке его обхода, легко проверить,
если вычислить знаки косых произведений [PiPi+1'Pi+1Pi+2]' = 1, , п (здесь
Рп+1 есть Р 1 , а Р![]()
![]()
![]() Р2 , т. е.
при программировании удобно добавить после точки Р две лишние точки,
совпадающие с точками Р1 и Р 2 соответственно). У выпуклого многоугольника
знаки указанных произведений либо все неположительны, либо все неотрицательны
(т. е. знаки ненулевых произведений совпадают). Если мы знаем направление
обхода, то знак косых произведений для выпуклого многоугольника определен: при
обходе по часовой стрелке все косые произведения неположительны, а против
часовой стрелки — неотрицательны.
Р2 , т. е.
при программировании удобно добавить после точки Р две лишние точки,
совпадающие с точками Р1 и Р 2 соответственно). У выпуклого многоугольника
знаки указанных произведений либо все неположительны, либо все неотрицательны
(т. е. знаки ненулевых произведений совпадают). Если мы знаем направление
обхода, то знак косых произведений для выпуклого многоугольника определен: при
обходе по часовой стрелке все косые произведения неположительны, а против
часовой стрелки — неотрицательны.
6.4.2. Проверка принадлежности точки
внутренней ![]() области многоугольника
области многоугольника
Задача. Пусть М — некоторая точка плоскости. Требуется опреДелить ее местонахождение относительно замкнутой ломаной, являющейся границей выпуклого многоугольника.
Решение. Пусть заданные своими координатами вершины
многоугольника Р 1 , Р 2 , Р п перечислены в порядке его обхода против часовой
стрелки. Тогда, если точка М лежит внутри многоугольника, то
ориентированный угол между векторами Ц М и PiPi+1 для любого i отрицателен. ![]() Поэтому
нам достаточно подсчитать значения косых произведений [Ц М, Ц Ц
+1],
Поэтому
нам достаточно подсчитать значения косых произведений [Ц М, Ц Ц
+1], ![]() , п; здесь, как и
, п; здесь, как и ![]() в п. 6,4.1, точка Р
п+1 совпадает с точкой Р 1. Если все полученные при этом значения отрицательны,
то точка М — внутренняя. Если же одно из них равно нулю, а все
в п. 6,4.1, точка Р
п+1 совпадает с точкой Р 1. Если все полученные при этом значения отрицательны,
то точка М — внутренняя. Если же одно из них равно нулю, а все ![]() остальные
отрицательны, то М принадлежит границе
остальные
отрицательны, то М принадлежит границе
![]()
многоугольника (убедитесь, что просто равенства нулю одного из значений недостаточно). В противном же случае точка М лежит вне нашего многоугольника.
Рассмотрим теперь произвольный многоугольник. Проведем горизонтальный луч из точки М, например, влево. Так как ломаная ограничена, то всегда легко указать на этом луче точку Р(х, у), заведомо лежащую вне многоугольника, образованного ломаной. Далее подсчитаем количество пересечений отрезка РМ с границей многоугольника, рассмотрев его пересечение с каждым из звеньев ломаной. Если количество таких пересечений равно нулю или четно, то точка М лежит вне многоугольника, в противном случае — внутри него.
На самом деле этот алгоритм нуждается в уточнении. При подсчете количества пересечений отрезка РМ со звеньями ломаной для каждого из пересечений важно удостовериться, что отрезок действительно пересек ломаную, а не просто касается нее. При этом возможны следующие особые случаи:
а) одно из звеньев ломаной целиком содержится внутри отрезка РМ;
б) звено ломаной касается отрезка РМ;
в) точка М лежит на одном из звеньев ломаной.
В последнем случае М принадлежит
границе многоугольника и в подсчете общего числа пересечений необходимости нет.
Для двух первых случаев поступим следующим образом. В случае а) пересечение
будем игнорироваты А в случае б) дополнительно проверим, «нижним» или «верхним»
концом звено ломаной касается отрезка РМ. Если точкой касания является «нижний»
конец звена, то пересечение игнорируется, а если «верхний», то засчитывается. С
учетом этого соглашения касание отрезка РМ границы многоугольника в одних
точках игнорируется (как и требуется с точки зрения алгоритма), а в других
точках считается дважды, что, однако, не изменяет четности числа пересечений, а
только она важна при поиске ответа на вопрос данной задачи. Если же отрезок
действительно пересекает ломаную в ее вершине, то по нашему соглашению число
пересечений как раз увеличится на единицу (пересечение с верхним ребром
засчитано не будет, а с нижним — будет). Например, на рис. 6.10 коли![]() чество пересечений для верхней из исследуемых точек
чество пересечений для верхней из исследуемых точек
будет равно четырем (касание засчитано дважды), а для нижней точки — трем (касание не учтено, а пересечение в вершине ломаной учтено один раз).
Рис. 6.10
Под простым мы понимаем такой многоугольник, граница
которого не имеет самокасаний и самопересечений. Пусть вершины Р Р Рп простого
многоугольника перечислены в порядке обхода его границы. Площадь произвольного
простого многоугольника с вершинами ![]() Рп, перечисленными в порядке его обхода
против часовой стрелки, равна ориентированной площади многоугольника
(определенной выше для треугольника). В аналитической геометрии доказывается,
что последняя представляет собой сумму ориентированных площадей
треугольников, образованных векторами ОЦ и ОР
Рп, перечисленными в порядке его обхода
против часовой стрелки, равна ориентированной площади многоугольника
(определенной выше для треугольника). В аналитической геометрии доказывается,
что последняя представляет собой сумму ориентированных площадей
треугольников, образованных векторами ОЦ и ОР
![]()
![]() п, где точка Рп+1
совпадает с точкой Р 1 , а О — произвольная точка (рис. 6.11).
п, где точка Рп+1
совпадает с точкой Р 1 , а О — произвольная точка (рис. 6.11).
Для вычисления обычной площади многоугольника нужно взять модуль ориентированной площади:
![]() (6,14)
(6,14)
где полагается Р = Р1. В качестве точки О в некоторых задачах бывает разумно выбрать одну из вершин
многоугольника. Если же в качестве точки О взять начало координат, то формула (6.14) запишется в другом виде, также удобном для программирования:
S = 1/2l(x1Y2 — Х2У1) + (хгуз — хзУ2)
+ ... + (хпУ1 — xwn)l ![]() 1/21x1(Y2 — уп) + Х2(уз — У1) + ...+ хп(У1 — уп (6.15) где (хр Yi) —
координаты точки Р .
1/21x1(Y2 — уп) + Х2(уз — У1) + ...+ хп(У1 — уп (6.15) где (хр Yi) —
координаты точки Р .
Вопросы и задания
1. ![]()
![]() Выпишите
все формулы, необходимые для реализации решения задачи из п. 6.4.2 проверки
принадлежности точки внутренней области произвольного многоугольника.
Выпишите
все формулы, необходимые для реализации решения задачи из п. 6.4.2 проверки
принадлежности точки внутренней области произвольного многоугольника.
2. Отрезок,
соединяющий две не соседние вершины многоугольника, называется его диагональю.
Составьте алгоритм проверки принадлежности диагонали внутренней ![]() области
соответствующего невыпуклого многоугольника.
области
соответствующего невыпуклого многоугольника.
З. Выпуклой оболочкой некоторого заданного множества точек называется выпуклый многоугольник, все вершины которого являются точками исходного множества. Составьте алгоритм построения выпуклой оболочки заданного конечного множества точек.
4. Составьте алгоритм нахождения расстояния от точки до простого многоугольника на плоскости, если многоугольник задан путем перечисления координат его вершин в порядке их обхода против часовой стрелки.
S 6.5. Геометрические объекты в пространстве
Несмотря на то что экран компьютера является частью плоскости, и, соответственно, компьютерная графика оперирует двумерными изображениями, наибольший эффект в компьютерных играх, рекламных роликах и различных презентациях достигается при создании на дисплее эффекта трехмерности. Достигается это различными способами, в частности путем проектирования трехмерных объектов на плоскость с учетом их взаимного расположения в пространстве и освещенности. Но прежде чем рассматривать подобные задачи, научимся аналитически описывать объекты трехмерного мира.
6.5, 1 . Основные формулы
Будем считать систему координат в пространстве правой, если системы координат хОу, yOz и гох являются правыми (соответствующее определение для системы координат на плоскости см. в S 6.1).
Определение 6. Скалярным произведением двух векторов а = (а , а , а ) и Ь = (Ь Ь Ь ) называется число (а, Ь), которое в координатах вычисляется по формуле
![]() (6.16)
(6.16)
Хотя мы ввели понятие скалярного произведения для правой декартовой системы координат, оно справедливо для любой декартовой системы координат.
Определение 7. Ненулевой вектор, перпендикулярный заданной плоскости, называется нормалью к ней.
Определение 8. Векторным произвеДением любых двух векторов а и Ь называется вектор с = [а, Ь], декартовы координаты которого определяются формулой
[а, Ь] = (ау•Ьг — а • Ь , а • Ь — а • Ь , а • Ь — ау• ьх). (6.17)
Векторное произведение (вектор с) характеризуется следующим образом:
1) вектор с ортогонален каждому из векторов а и Ь;
2) вектор с направлен так, что тройка векторов а, Ь, с является правой;
З) длина вектора с равна произведению
длин векторов а и Ь на синус угла между ними, т. е. ![]() sin (Р.
sin (Р.
Свойства 1)—3) определяют вектор с в пространстве в любой декартовой системе координат правой ориентации однозначно.
Приведем для примера доказательство первого свойства. Чтобы доказать, что вектор с = [а, Ь] перпендикулярен плоскости, определяемой векторами а и Ь, достаточно показать, что скалярные произведения (а, [а, Ь]) и (Ь, [а, bl) равны нулю. Для первого из них мы имеем:
(а, [а, Ь]) = ах(ау• ьг а • Ь ) +
ау(а; ьх ![]() + az(ax• Ьу
+ az(ax• Ьу ![]()
Взаимное расположение векторов а и Ь и векторного произведения показано на рис. 6.12.
![]()
Треугольник ОАВ ориентирован
положительно, если ![]() на него смотреть в пространстве из конца
вектора [а, Ь]. Вектор нормали, имеющий такую же длину, но противоположное
направление, определяется как [Ь, а].
на него смотреть в пространстве из конца
вектора [а, Ь]. Вектор нормали, имеющий такую же длину, но противоположное
направление, определяется как [Ь, а].
![]()
В аналитической геометрии часто
используются так![]() же следующие свойства векторного
произведения:
же следующие свойства векторного
произведения:
![]()

Из двух последних свойств следует, что векторное произведение двух любых коллинеарных векторов равно нулевому вектору.
Заметим, что если векторы а и Ь лежат в плоскости хОу, то длина вектора их векторного произведения равна модулю их косого произведения:
![]()
Именно поэтому ранее мы использовали для косого произведения обозначение, принятое для векторного произведения.
6.5.2. Определение пересечения прямой линии и треугольника в пространстве
![]() Пусть нам требуется
определить, проходит ли прямая
Пусть нам требуется
определить, проходит ли прямая ![]() линия в пространстве сквозь треугольник.
Решение такой задачи имеет важное значение в трехмерной компьютерной графике, в
частности при исследовании проблемы загораживания объектами друг друга.
Рассмотрим один из подходов к ее решению.
линия в пространстве сквозь треугольник.
Решение такой задачи имеет важное значение в трехмерной компьютерной графике, в
частности при исследовании проблемы загораживания объектами друг друга.
Рассмотрим один из подходов к ее решению.
Определение 9. Проекцией называется
отражение пространства более высокого порядка на пространство более низкого
порядка (в нашем случае — трехмерного на двумерное). ![]()
Метод проекции часто используется для
замены исходной задачи на задачу «меньшей размерности», т. е. решается задача в
пространстве более низкого порядка, ![]() где нам уже известны способы ее решения.
где нам уже известны способы ее решения.
Пусть нам требуется определить,
проходит ли данная бесконечная прямая линия через заданный треугольник РIР2Рз.
Вначале вычислим координаты точки Q, в которой бесконечная прямая линия
пересекает плоскость, в которой лежит треугольник. Затем выполним ортого![]() вальное проецирование треугольника РIР2Рз и точки Q на плоскость хОу. Для этого
достаточно приравнять
вальное проецирование треугольника РIР2Рз и точки Q на плоскость хОу. Для этого
достаточно приравнять ![]() г-координаты точек Р 1 , Р2 , Рз и Q
нулю. При этом мы получаем треугольник Р1'Р5Рз' и точку Q'. Задача, эквива
г-координаты точек Р 1 , Р2 , Рз и Q
нулю. При этом мы получаем треугольник Р1'Р5Рз' и точку Q'. Задача, эквива![]() лентная исходной, — в двумерном пространстве определить, принадлежит ли точка
Q' треугольнику Р1'ЦЦ, уже была решена нами в 6.4.2.
лентная исходной, — в двумерном пространстве определить, принадлежит ли точка
Q' треугольнику Р1'ЦЦ, уже была решена нами в 6.4.2.
При проецировании иногда, в результате потери информации, возникает неоднозначная ситуация, когда мы не сможем ответить на поставленный вопрос. Происходит это тогда, когда треугольник проецируется в отрезок на плоскости. Таким образом, чтобы использовать описанный выше алгоритм решения задачи, перед проецированием необходимо выполнить проверку на вырождение. Если вектор нормали треугольника перпендикулярен оси z (а это и есть условие вырождения), то проецирование будем выполнять на плоскость yOz. Если и она окажется вырожденной, то будем использовать проекцию на ПЛОСкость zOx. Поскольку вектор нормали не может быть перпендикулярен одновременно всем трем осям, по крайней мере одна из проекций окажется невырожденной.
6.5.3. Вращение точки вокруг заданной прямой
в пространстве
![]() Вам наверняка
приходилось наблюдать за одним из впечатляющих эффектов трехмерной компьютерной
графики — вращением выпуклых или невыпуклых многогранников в пространстве.
Насколько сложно реализовать подобное вращение? Если мы научимся вращать
требуемым образом одну точку, то, организовав соответствующее движение всех
вершин многогранника, несложно будет добиться нужного результата и для
многогранника в целом.
Вам наверняка
приходилось наблюдать за одним из впечатляющих эффектов трехмерной компьютерной
графики — вращением выпуклых или невыпуклых многогранников в пространстве.
Насколько сложно реализовать подобное вращение? Если мы научимся вращать
требуемым образом одну точку, то, организовав соответствующее движение всех
вершин многогранника, несложно будет добиться нужного результата и для
многогранника в целом.
Пусть требуется повернуть точку с координатами Ао(хо, уо, го) относительно оси, заданной единичным вектором п(хп, уп, г п), проходящим через начало координат, на угол (Р. Обозначим через Ah(xn, Л, Zh) ортогональную проекцию точки Ао на ось вращения (рис. 6.13). Точка Ао и вектор п определяют ПЛОёКОСТЬ Р, перпендикулярную оси вращения. Таким образом, задача сводится к нахождению координат точки „41 , принадлежащей Р, такой что ZAoAr41 = (Р.
Для решения этой задачи будет построена новая система координат, в которой координаты точки „41 определяются достаточно просто, а затем найденные координаты будут переведены в исходную систему координат.
х
Рис. 6.13
Найдем ортогональную проекцию Ah(xn, [Л, 4) точки Ао на ось вращения. Вектор AhAo ортогонален вектору п, поэтому их скалярное произведение равно 0:
хп(хо — Xh) + Уп(уо — Уп) + zn(zo — Zh) О (6.18) Вместе с тем вектор 0Ah (хю уп, Zh) коллинеарен вектору п, поэтому
![]() h.xn; h•yn;
h.xn; h•yn; ![]() (6.19)
(6.19)
h = (хп•хо + уп • уо + ![]() + + г; ) _ — (хп• хо + уп• уо + zn•
го).
+ + г; ) _ — (хп• хо + уп• уо + zn•
го).
Теперь из (6,19) мы знаем координаты Ар следовательно, и сам вектор AhAo, и можем вычислить его длину r. Разделив этот вектор на его длину, получим вектор а(х у ) единичной длины.
Введем новую декартову правую систему координат с центром в точке О так:
1. Направим ось 2' вдоль оси, задаваемой вектором п (базисный вектор, который мы обозначим К', при этом совпадет с вектором п).
![]()
2. Направим ось х? в направлении вектора AhAo (обозначим соответствующий базисный вектор i', в нашем случае он совпадает с вектором а по построению).
З. Вычислим координаты направляющего вектора оси у' из условия правой ортогональной тройки базиса:
Ј' = [К', i'] = (yn•za — z п •у а , z 71 •х а — х п •z а , х 71 •у а — уп•ха).
То есть координаты базисных векторов новой системы через координаты старой можно выразить следующим образом:
i' х •i + уа•ј + «К,
ј' = (у п •z а ть —z •у а)i + (zn•xa — ![]() +
(х •у —у •х )k, (6.20) К' = xn•i + уп•ј + z «К.
+
(х •у —у •х )k, (6.20) К' = xn•i + уп•ј + z «К.
Координаты искомой точки „41 в новой системе координат равны (r cos р, rsin ф, h) (см. уравнение окружности (6.9)).
0х41 =x1'i+ У1ј + 21 •k = rcos p•i' + rsin р•ј' + h•k'. (6.21)
Подставляя в правую часть (6.21) выражения (6.20), получим координаты искомой точки в изначальной системе координат:
![]() — rcos«p уа + rsin
— rcos«p уа + rsin ![]() + z •х ) + h•yn• (6.22)
+ z •х ) + h•yn• (6.22) ![]() = rcosp za + rsinp (хп•уа уп•ха) + .
= rcosp za + rsinp (хп•уа уп•ха) + .
Вопросы и задания
1. Проверьте, что (Ь, [а, Ь]) = О для любых векторов а и Ь.
2. Докажите, что если векторы а и Ь лежат в плоскости хОу, то длина их векторного произведения равна модулю их косого произведения: l[a, = lax•by — ay•bxl.
З, Модифицируйте алгоритм из п. 6.5.3 так, чтобы он эффективно работал в случае необходимости поворота относительно заданной оси на заданный угол сразу нескольких точек.
4. Составьте алгоритм определения видимости линий, с помощью которых изображается ортогональная проекция выпуклого многогранника на плоскость хОу.
5. На любом известном вам языке программирования напишите программу вращения многогранника относительно некоторой оси.
Заключение
В данной главе вы познакомились с базовыми понятиями вычислительной геометрии, на основе которой построено большинство алгоритмов компьютерной графики. Мы надеемся, что, используя новые для вас понятия косого и векторного произведений двух векторов, а также известного из курса геометрии скалярного произведения, вы научились решать большинство предложенных задач вычислительной геометрии достаточно простым способом.
Многие алгоритмы вычислительной геометрии и компьютерной графики достаточно сложны и продолжают в настоящее время развиваться и совершенствоваться. Мы ждем открытий в этой области и от вас!
Приложение
![]()
Реконструкция аналогового сигнала
Исходные цифровые данные
|
|
|
|
||
|
|
|
|
|
|
![]()
![]() Входной поток аудиоданных
Входной поток аудиоданных
|
|
|
||||||||||||||||||||||||||||||||||
многочлены
Цифро-аналоговый
Ступенчатый аналоговый сигнал преобразователь
Выход
Предметный указатель
![]()
Абстрактные вычислительные конструкции 210
Алгебра 148
Алгебра логики 148
Алгоритм 201
JPEG 143
МРЗ 143 MPEG 144 ![]() вычисления квадратного корня «в
столбик» 202
вычисления квадратного корня «в
столбик» 202
перевода
Р-ичной дроби в десятичную 40 бесконечной периодической дроби 42 десятичной дроби в Р-ичную 48
целого числа
из Р-ичной системы в десятичную 38
из двоичной системы в десятичную 39
из десятичной системы в Р-ичную 45
перечисления натуральных чисел в Р-ичных системах
сжатия с регулируемой потерей информации 141
счисления 26 JPEG 143
MPEG 144
МРЗ 143 по Посту 220 по Тьюрингу 219 поиска бинарного 237
минимального и максимального элементов 236 последовательного 235 получения дополнительного кода отрицательного числа 68 построения СДНФ по таблице истинности 182 построения СКНФ по таблице истинности 183 «Решето Эратосфена» нахождения простых чисел 202
сжатия:
RLE 137
Лемпеля—Зива 139 метод упаковки 133 обратимый 101, 132
Хаффмана 135
Алгоритмическая конструкция ветвящаяся 208
![]()
последовательная 208 рекурсивная 208 циклическая 208
Алгоритмически неразрешимая задача 209, 224
Алфавит входных символов алгоритма 211
мощность 267 позиционной системы счисления 16, 19 системы счисления 13
размерность 13
Аналого-цифровой преобразователь (АЦП) 123
Арифметика в ограниченном числе разрядов над целыми числами
71, 72 особенности реализации 73
Арифметика вещественных чисел выравнивание порядков 81 вычитание 81 деление 83 нормализация 76, 83 округление 85
сложение 81
особенности реализации 84
умножение 83
Арифметические операции в позиционных системах счисления вычитание 33 деление 35 сложение 32 умножение 33
АЦП (аналого-цифровэй преобразователь) 123
Базис позиционной системы счисления 14
Байт 253
Бинарный поиск 237 Бит 253
![]() Булева функция 176 полная система
булевых функций 190
Булева функция 176 полная система
булевых функций 190
в
Вектор 286 длина 286 коллинеарный 287 противоположно направленный 287
свободный 286
сонаправленный 287
нормали 293
Векторное произведениеВыпуклость многоугольников, проверка 308 312
Выравнивание порядков 81
Высказывание 149 простое 150
Вычислимые функции 228
Вычислительная геометрия 284 Вычислительный процесс 230
Глубина цвета (цветности) 110 кодирования звука 124
д
Двоичное кодирование 253
Диапазон значений беззнаковых целых чисел 66 знаковых целых чисел 71 вещественных чисел 81
Дизъюнктивная нормальная форма (ДНФ) 179
Дискретизация 65, 97—99 временная 98, 122 пространственная 97 Длина слова 211
з
Законы алгебры логики ассоциативности
165 двойного отрицания 165 де Моргана 165 дистрибутивности 165 ![]()
![]() коммутативности 165
коммутативности 165 ![]() идемпотентности 165 исключенного
третьего 165 поглощения 165 поглощения (нуля и единицы) 165 противоречия 165
идемпотентности 165 исключенного
третьего 165 поглощения 165 поглощения (нуля и единицы) 165 противоречия 165
Грассмана 105
Запись MIDI 127
аналоговая 122 звука 122 цифровая 122
и
Избыточность информации 130 ![]()
Изображение растровое 103
Информационный вес символа 268, 273
Информация 250 количество 252, 253
полезная 251
Исполнитель алгоритма 201
Импульсно-кодовая модуляция звука 123
Итерация 240, 241
Канонические формы формул 178
Квантование 99 звука 122, 124
цвета 104
цветового пространства 109, 117
Код дополнительный 68 обратный 68
прямой 67 символа 90
Хаффмана 135, 277
Кодирование двоичное 258 избыточное 131 однозначное 258 ![]()
Кодировка
ASCII 91
Unicode 94
Колориметрия 105
Компьютерная арифметика вещественная 84 целочисленная 73 К-разрядная 72
Конъюнктивная нормальная форма (КНФ) 180
Координаты вектора 286
Косое произведение 291
л
Логическая переменная 164
Логическая формула 164 равносильная, или эквивалентная 164
Логическая функция 176
Логические операции 153 дизъюнкция 153—155 элементарная 180
импликация 153, 157 конъюнкция 153, 154 элементарная 179
отрицание 153, 160 строгая, или разделительная дизъюнкция 153, 155, 156 эквивалентность 153, 159
Логический элемент (вентиль) 193
м
Мантисса 75
Машина
Поста 221
Тьюринга 210, 212, 219
Машинный нуль 76
Мера количества информации 252, 253, 261
Метод
РСМ (импульсно-кодовой модуляции) 123 быстрого вычисления натуральной степени вещественного числа
233 минимизирующих карт 187 сжатия с регулируемой потерей информации 141 умножения, «русский» 233
Минимальная ДНФ 186
Минимизация в классе ДНФ 186—188
Модель цветовая 106 СМУК 112, 115
![]() 115
115
RGB 106, 107
Мощность алфавита 267
н
Насыщенность 107, 115
Нормализация 83
Нормализованная форма записи чисел 76 мантисса 75, 76 порядок 75, 76
Нормаль к прямой 293 к плоскости 312
Нормальная форма 179, 180 Нулевая избыточность 55
о
Обратный код 68
Оптимальное кодирование 256
Ориентированная площадь 289, 290
Ориентированный угол 288, 291
Основание позиционной системы 14, 24 Оцифровка звука 123
п
Передискретизация 128
Переключательная схема 173 равные 174 синтез 175
Пиксель 103
Площадь ориентированная 289, 290
Погрешность абсолютная 78 относительная 78
Подход к измерению информации алфавитный 252, 267 объективный 253 содержательный 251
субъективный 252
Полные системы булевых функций 190
Порядок нормализованного числа 75
Предикат 150
Представление информации графической 96, 102 векторное 101, 102 растровое 101—103 звуковой 120, 122, 124
текстовой 89 числовой 20
нормализованное 76, 77 целых отрицательных 68
целых положительных 66
Префиксный код 137, 278
Принцип позиционности 14
Проблема самоприменимости или останова 225, 226
Проекция 314
Произведение векторов векторное 312 скалярное 288, 312 псевдоскалярное, или косое 291
Прямой код 67
Равносильные, или эквивалентные формулы 164
Размерность алфавита 13
Разряд 64 Растр 103
с
Свойства алгоритма детерминированность 204, 205 дискретность 204 конечность 204 массовость 205
понятность 204 результативность 204
Система кодировки 91—93
Система координат правая 285
левая 292 ![]()
Система счисления 13 аддитивно-мультипликативная 13 восьмеричная 15 двоичная 15 нетрадиционная 15 позиционная 13 базис 14, 17 основание 14, 24
цифры 16, 19 смешанная РФ-ичная 51 традиционная 14 ![]() факториальная 15, 16 Фибоначчиева
15, 16, 58, 59 шестнадцатеричная 15 уравновешенная 13, 16, 58 Р-ичная 14
факториальная 15, 16 Фибоначчиева
15, 16, 58, 59 шестнадцатеричная 15 уравновешенная 13, 16, 58 Р-ичная 14
Сжатие информации 101
![]()
![]()
![]()
Слово алфавита 211 входное 212 выходное 212 длина 211
Сложность алгоритма 230 временная 231 теоретическая 231
Сложность объекта (явления) 280
Совершенная нормальная форма дизъюнктивная (СДНФ) 179 конъюнктивная (СКНФ) 180
Сортировка 238 внутренняя 239 вставками 243
выбором 241 обменная методом «пузырька» 239 слиянием 244
Способ минимизации ДНФ 187
Среда исполнителя 203
![]()
Стандарт
MIDI 127 кодирования ASCII 91 сжатия МРЗ 143
Стрелка Пирса 192
Сумматор 194
Схема Горнера 39, 41 ![]()
т
Таблица истинности 154—157, 159—161 кодирования ASCII 92 кодирования КОИ-8 93 кодирования Windows-1251 94
сложения в двоичной системе 32
сложения в троичной системе 32
сложения в шестнадцатеричной системе 32
умножения в двоичной системе 34
умножения в троичной системе 34
умножения в шестнадцатеричной системе 35
частоты встречаемости символов 135
Тавтология 166
Тезис поста 221
Тьюринга 218
Теорема
о представлении произвольного натурального числа в виде степенного ряда 20
о взаимосвязи Р-ичных и фичных систем счисления, где ![]() Р = 51
Р = 51
Чёрча 227
Точность вычислений 48
Трехкомпонентная теория цвета 105 Триггер 196
Угол между векторами 288 ориентированный 288, 291
Универсальный исполнитель 219
Уравнение ![]() окружности 297
окружности 297
прямой общее 293 нормированное 295 параметрическое 296
Условие, импликация 153, 157
Форма записи чисел нормализованная 76 развернутая 25, 26 свернутая 25, 26
Форма представления логической функции дизъюнктивная нормальная (ДНФ) 179 каноническая 179 конъюнктивная нормальная (КНФ) 180
нормальная 179
совершенная 179 совершенная дизъюнктивная нормальная (СДНФ) 179 совершенная конъюнктивная нормальная (СКНФ) 180
Формальная логика 149
Формула логическая 164 Стирлинга 265
Хартли 259—261
Шеннона 270, 271
ц
ЦАП (цифро-аналоговый преобразователь) 123
Цветовой оттенок, или цветовой тон 107
RGB 106, 107 аддитивная 112 субтрактивная 113
Цифра системы счисления 24
Частота встречаемости 270 дискретизации 124
Чистый цветовой тон 115
ш
Штрих Шеффера 191
Э
Энтропия 272
Эффективность алгоритма 232
я
Яркость 107, 116
[1] Фактически операции сложения, вычитания и умножения в К-разрядном беззнаковом представлении соответствуют математическому понятию «арифметические операции по модулю 2k » (сравнение по модулю 2 k).
[2] При выполнении этого задания следует нормализовать мантиссу результата соответствующего арифметического действия, а затем округлить ее.
[3] См. S 3.10 «Элементы схемотехники. Логические схемы».
[4] Пример
приведен в книге В. А. Успенского «Машина Поста» . ![]()
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.