Математика

Урок № ______ Дата ___________ Алгебра 8 класс

Тема урока:  «Квадратное неравенство. Решение квадратного неравенства с помощью графика квадратичной функции».

Цели  урока:

Образовательная: объяснить  правило  решения  квадратных  неравенств; формировать  умение  решать  различные  неравенства;

Развивающая: формирование  элементов  алгоритмической  культуры;

Воспитательная: формирование  отношения  к  математике  как  к  части  общечеловеческой  культуры.

Задачи  урока:

-                   Узнать  алгоритм  решения  квадратных  неравенств.

-                   Уметь  применять  графическую  иллюстрацию.

-                   Использовать  приобретенные  знания  и  умения  в  практической  деятельности для  построения  и  исследования  простейших  математических  моделей.

Тип  урока:  урок  ознакомления  с  новым  материалом.

Ход урока

                  I.                        Организационный момент.

Приветствие,  проверка готовности к уроку.                 

Здравствуйте уважаемые гости и ребята! Ребята у нас сегодня на уроке присутствуют гости, давайте же мы проведем наш урок так, чтобы гостям не было скучно, а нам нудно. Для начала зарядимся хорошим, активным настроением, для этого проведем разминку.

Психологический настрой (разминка, устно):   

1.                  Произведение чисел 22600 и 0 увеличь на 52. (52)

2.                  Частное чисел 777 и 1 уменьши на 77 (700)

3.                  Увеличь 860 в 10 раз. (8600)

4.                  Увеличь 810 на 10. (820)

5.                  Число 720 уменьши в 8 раз. (90)

              II.                        Актуализация знаний. «Никогда не берись за последующее, не усвоив предыдущего» проверим себя, всё ли было усвоено на прошлых уроках. Для этого проведём разминку по изученному материалу.

1 Задание. Устная работа

1. Какая функция называется квадратичной? (Функция вида у = ах² + bх + с называется квадратичной).

2. Что мы знаем о свойствах коэффициента?

3. Не выполняя построения графика функции у =  – 3х²  – 6х + 1, ответьте на вопросы:

·                     Какая прямая служит осью параболы? (х₀ =  – 1)

·                     Каковы координаты вершины параболы? ( – 1; 4)

·                     Чему равно наименьшее и наибольшее значение функции? (у_{наибольшее} = 4; у_{наименьшее} не существует).

           III.                        Формирование новейших понятий и способов действий.

Учитель: перед вами несколько математических выражений. Скажите, какие из них вам знакомы, как они называются, и выделите те, которые вам пока не знакомы.

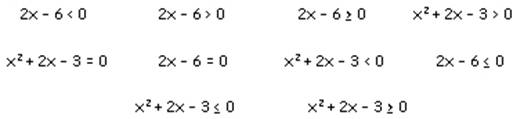
(Линейные уравнения и неравенства и квадратное уравнение знакомы; незнакомы - квадратные неравенства).

Учитель: Итак, ребята, как вы уже догадались,… сегодня мы с вами уделим внимание…  

Учащиеся: квадратные неравенства.

Учитель: тема сегодняшнего урока “Квадратное неравенство. Решение квадратного неравенства с помощью графика квадратичной функции”.

Мне хочется вас угостить конфетами, а теперь хочу вас попросить сесть в парах по цвету ваших сладостей.

Парная работа с последующим обсуждением.

Составьте определение квадратного неравенства

1.   Определение: неравенства вида ах²+bx+c>0, ах²+bx+c<0, ах²+bx+c0, ах²+bx+c0, где a, b, c – действительные числа, при чем а0, х – переменная, называется квадратным неравенством.

2. Решение квадратных неравенств помощью графика квадратичной функции:

а) определить направление ветвей параболы по знаку коэффициента «а»;

б) выявить количество общих точек  графика с осью ОХ (нули функции): Д=0; Д<0; Д>0.

в) изобразить схематически график функции.

г) определить знаки на промежутках и выбрать решение.

Сегодня мы будем рассматривать:

Групповая работа «Снежный ком»:

I Случай : а>0, D>0     а) х2 - 3х +2 > 0;         x1=1; x2=2  Ответ: (–¥; 1)(2; +¥) Реши неравенства, используя решение а): б) х2 - 3х + 2  0; в) х2 - 3х + 2 <0; г) х2 - 3х + 2  0; Вывод: квадратное неравенство ах2+bx+c>0, при  а>0, D>0 имеет решение (–¥; х1)(х2; +¥) Квадратное неравенство ах2+bx+c<0 имеет решение (х1; х2). Решения неравенств ах2+bx+c0 и ах2+bx+c0 отличаются от них  квадратными скобками. При а<0 умножим обе части на «-1», поменяв при этом знак неравенства.

II Случай : а>0, D=0     а) х2+6х +9> 0;           х = -3 Ответ: (–¥; -3)(-3; +¥) Реши неравенства используя решение а): б) х2+6х +9 0; в) х2+6х +9<0; г) х2+6х +9 0; Вывод: квадратное неравенство ах2+bx+c>0, при  а>0, D=0 имеет решение(–¥; х)(х; +¥) Квадратное неравенство ах2+bx+c<0 не имеет решения. Решение неравенства ах2+bx+c0 (–¥;+¥) Решение неравенства ах2+bx+c0 число х При а<0 умножим обе части на «-1», поменяв при этом знак неравенства.

III Случай : а>0, D<0    а) х2-4х +8> 0;             Корней нет Ответ: (–¥;+¥) Реши неравенства: б) х2-4х +8 0; в) х2-4х +8<0; г) х2-4х +8 0; Вывод: квадратное неравенство ах2+bx+c>0 и ах2+bx+c0  при  а>0, D<0 имеют решение (–¥;+¥).  Квадратные неравенства ах2+bx+c<0 и ах2+bx+c0    не имеют решения. При а<0 умножим обе части на «-1», поменяв при этом знак неравенства.

                       IV.            Мотивация.

Находят ли применение эти квадратные неравенства  в окружающем нас мире?! А может это просто прихоть математиков?!

       Презентация «Квадратные неравенства в окружающем мире»

                           V.            Физкультминутка.

Цель: снятие зрительного напряжения.

Нарисуй глазами треугольник.
Теперь его переверни вершиной вниз.
И вновь глазами ты по периметру веди.
Рисуй восьмерку вертикально.
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись.
Зажмурься крепко, не ленись.
Глаза открываем мы, наконец.
Зарядка окончилась. Ты – молодец!

                       VI.            Применение знаний, формирование умений и навыков

Домашняя работа: карточка

Разноуровневое домашнее задание

                    VII.           Итог урока. Сдаются оценочные листы с рефлексией.

Рефлексия.

1.     На уроке я работал                                             активно / пассивно

2.     Своей работой на уроке я                                  доволен / не доволен

3.     Урок для меня показался                                   коротким / длинным

4.     За урок я                                                              не устал / устал

5.     Моё настроение                                                  стало лучше / стало хуже

САМОАНАЛИЗ открытого урока

1.                     ХАРАКТЕРИСТИКА КЛАССА.

8 класс имеет средний уровень подготовленности. Качество знаний в данном класс 50%. Дети заданную работу стараются выполнять по мере своих возможностей. Для учащихся данная тема является одной из новых тем. Можно отметить учениц Мустакимову Карину, Чупик Викторию и Кошля Анастасию, которые по сравнению с остальными учащимися умеют применить изученный теоретический материал на практике.

2.                     Тема урока: «Квадратное неравенство. Решение квадратного неравенства с помощью графика квадратичной функции». На эту тему отводится 3 часа, и углубленно изучается в начале 4 четверти. И открытый урок был проведен на 1 уроке, и так как тема очень обширная.

Цели  урока:

Образовательная: объяснить  правило  решения  квадратных  неравенств; формировать  умение  решать  различные  неравенства;

Развивающая: формирование  элементов  алгоритмической  культуры;

Воспитательная: формирование  отношения  к  математике  как  к  части  общечеловеческой  культуры.

Задачи  урока:

-                  Узнать  алгоритм  решения  квадратных  неравенств.

-                  Уметь  применять  графическую  иллюстрацию.

-                  Использовать  приобретенные  знания  и  умения  в  практической  деятельности для  построения  и  исследования  простейших  математических  моделей.

Тип  урока:  урок  ознакомления  с  новым  материалом.

3.                     На данном уроке учащиеся были немного скованы. Волновались. Но все же, то что было запланировано, все было проведено. Старалась показать возможности учащихся, как они работают устно, как в парах  и у доски.

4.                     Этапы урока выдержаны, поставлены четко. Что означает изменений вводить никаких не надо. Лишь плохой словарный запас учащихся  сильно отражается в процессе урока, поэтому нужно требовать, чтобы они умели обосновывать свои ответы, говорит у доски. И над этим на каждом уроке работаю.

Подготовила учитель математики: Темирханова А.С.

Скачано с www.znanio.ru