
А.Ж. Дюсекеева
учитель ГУ лицея, г. Аксу
УЧЕБНЫЙ ЛИСТ
Глава «Квадратные уравнения».
В результате изучения тем нужно
|
Знать: - определение квадратного уравнения; - способы решения квадратных уравнений; - формулы для нахождения корней квадратных уравнений; - алгоритм решения дробно-рациональных и биквадратных уравнений; - теорему Виета. |
Уметь: - находить корни квадратного уравнения; решать дробно-рациональные и биквадратные уравнения; - составлять уравнение по заданным его корням. |
ЛИТЕРАТУРА:
1. А. Абылкасымова,Алгебра учебник 8 класса общеобразовательной школы . Алматы «Мектеп», 2012г
2. С.К.Тулеубаева ,В.Е.Корчевский Алгебра 8 класс. Сборник задач. Алматы «Мектеп», 2012г.
3.К.Базаров, Алгебра 8 класс. Дидактические материалы. г Алматы: «Мектеп», 2004г.
Помни, что работать нужно по алгоритму!
Не забывай проходить проверку, делать пометки на полях, заполнять рейтинговый лист темы.
Пожалуйста, не оставляй без ответа, возникшие у тебя вопросы.
Будь объективен во время взаимопроверки, это поможет и тебе, и тому, кого ты проверяешь.
ЖЕЛАЮ УСПЕХА!
Теория без практики мертва или бесплодна
Практика без теории невозможна или пагубна
Для теории нужны знания, для практики сверх того, и умения.
А.Н.Крылов
.
I. Полные и неполные квадратные уравнения
1) Прочитай текст:
Уравнение вида ах 2 + вх + с = 0, где х - переменная, , а, в и с - некоторые действительные числа, если а≠ 0, называется уравнением второй степени.
Если а = 0, то уравнение примет вид BX + C = 0 и будет уравнением первой степени .
Неполные квадратные уравнения:
Если в = 0, то уравнение примет вид ах2 + с = 0
Если с = 0, то уравнение примет вид ах2 + вх = 0
Если с = 0, в=0, то уравнение примет вид ах2 = 0
Д= в2-4ас Если D <0, то действительных корней нет.
Если D =
0, то корни совпадают и равны х1/2=![]()
Если D >0,то,извлекая корень, получим х1/2=![]()
Это и есть формула для решения квадратного уравнения.
№1. Какой из данных уравнений является а) квадратным уравнением б) приведенным квадратным уравнением : по (1б)
1) 2х+3=0; 2) х2-19х=0; 3) х3-х2+5=0; 4)3х3-0,4х2-х=0; 5) -3х-х2+7=0
№2. Решить уравнения а) :3х2+4х-7=0
б) 9х2-4=0
в) 2=7х2+2 г) ![]() х2+
х2+![]() е)2х2-2х+0,5=0
к)
е)2х2-2х+0,5=0
к) ![]() а=а2+4 (по 2б.)
а=а2+4 (по 2б.)
Алгоритм решения приведенного квадратного уравнения путем выделения квадрата двучлена:
Х2+px+c=0
1) х2+2px+q=0
2) х2+2px+p2=p2-q
3) (x+p)2=p2-q
4) x+p = ![]() , если
p2-q
, если
p2-q![]() 0
0
5) х = -p ![]()
№3. Решить уравнение: Х2-6х+8=0 (2б.)
Определение. Биквадратное уравнение — это любое уравнение вида:
ax4 + bx2 + c = 0, где a, b, c — любые числа, причем a ≠ 0.
Примеры. Вот несколько биквадратных уравнений: x4 −
5x2 + 6 = 0; 3x4 − 2x2 +
1 = 0;
x4 − 1 = 0.
Как решать биквадратные уравнения: общая схема
Биквадратные уравнения легко сводятся к обычным квадратным с помощью замены переменной. Поэтому алгоритм выглядит следующим образом:
1. Ввести новую переменную: t = x2
2. Подставить эту переменную в исходное уравнение. Мы получим обычное квадратное уравнение, которое решается через дискриминант: ax4 + bx2 + c = 0 ⇒ at2 + bt + c = 0;
3. Решаем полученное квадратное уравнение. Получим корни t1 и t2;
4. Подставляем эти корни в формулу замены переменной: x2 = t1и x2 = t2;
5. Решаем эти два уравнения — получаем искомые корни биквадратного уравнения.
№4.Решите уравнение:
а) x4 − 13x2 + 36 = 0 ( 3б.)
Сумма корней приведенного квадратного трехчлена x2 + px + q = 0 равна его второму коэффициенту p с противоположным знаком, а произведение – свободному члену q,
т. е.x1 + x2 = – p и x1 x2 = q Если а=1 (приведенная форма x2 + px + q = 0), то (теорема Виета)
 .
.
№1. Решите уравнение с помощью теоремы Виета: а) х 2 + 2 х - 3 = 0. (2б)
б) х 2 + 6 х + 9 = 0. (2б)
Обратная Теорема Виета. Если числа x1 и x2 удовлетворяют соотношениям x1 + x2 = – p и x1 x2= q, то они удовлетворяют квадратному уравнению x2 + px + q = 0.
№2. Составить квадратное уравнение, если х1= 2+![]() и х2 =2-
и х2 =2-![]() (2б.)
(2б.)
Самый распространённый, а иногда и единственно
возможный метод решения уравнений с модулем – раскрытие модуля согласно
определению:
![]()
№3. Решить уравнение: ![]() . 4(б.)
. 4(б.)
III. Дробно-рациональные уравнения.
Если в рациональном уравнении есть деление на выражение, содержащее переменную (x), то уравнение называется дробно-рациональным.
Дробные рациональные уравнения обычно решаются следующим образом:
|
1) находят общий знаменатель дробей и умножают на него обе части уравнения; 2) решают получившееся целое уравнение; 3) исключают из его корней те, которые обращают в ноль общий знаменатель дробей, т.е. определяют посторонние корни |
а) 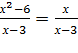 (2б.) б)
(2б.) б) ![]() (3б.)
(3б.)
в) 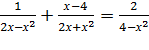 (4б.)
(4б.)
Итого: 38 баллов
«5» - 36-38б. «4» - 28-35б. «3» - 19-27б.
Рефлексия.
Что у вас получилось? А что не получилось?
В чем были проблемы?
Кто чувствовал себя сегодня неуверенно?
А кто испытал чувство удовлетворения от проделанной работы?
Спасибо за урок.
РЕЙТИНГОВЫЙ ЛИСТ
По теме: «Квадратные уравнения»
Ф.И. , класс .
|
№ |
Задания |
Max баллов |
Полученные баллы |
Кто проверил |
Кого проверил |
Оценка |
|
I |
№1 №2 №3 №4 |
. |
|
|
|
|
|
II |
№1 №2 |
|
|
|
|
|
|
III |
|
. |
|
|
|
|
|
итог |
|
|
|
|
|
|
|
Итого: |
||||||
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.