математика

Обобщающий урок по теме «Квадратные уравнения»

8 класс

Цели урока:

·         Образовательные: закрепление и обобщение знаний учащихся полученные при изучении темы, отработка умений и навыков по решению квадратных уравнений различного вида различными способами, выработка умения выбрать нужный рациональный способ решения.

·         Развивающие: развитие логического мышления, памяти, внимания, умений сравнивать и обобщать, умения выступать с самостоятельными суждениями и отстаивать их.

·         Воспитательные: воспитание трудолюбия, взаимопомощи, математической культуры, умение работать в группах, развивать познавательную активность и логическое мышление учащихся, развития интереса к предмету.

·         Оборудование: проектор, компьютер,  презентация, карточки для проведения рефлексии, карточки с заданиями, индивидуальные координатные плоскости, карты результативности учащихся, тесты

ХОД УРОКА

·                     I. Организационный момент.  Настроимся на урок.

Здравствуйте, ребята! Я очень рада всех видеть вас сегодня и надеюсь на совместную плодотворную работу .

Готовясь к сегодняшнему уроку, я натолкнулась на одну интересную историю: несколько десятилетий назад в Америке была объявлена премия тому автору, который напишет книгу «как человек без математики жил». Премия осталась не выданной. Как вы думаете, почему? (Ответы учащихся). Да, вы правы ни один из авторов не смог доказать, что человеку математика не нужна, никто не смог изобразить жизнь человека без применения каких-либо математических знаний. Вот и нам с вами на уроке не обойтись без набора определенных знаний и умений.

 II. Основная часть урока

Посмотрите на доску, что вы видете?      27х2 +5х+2019=0

Правильно –квадратное уравнение.

Сформулируйте определение. Что такое квадратное уравнение?

  Хорошо.  Кто может выписать на доске коэффициенты этого квадратного уравнения?               а=27  в =5 с = 2019. Посмотрите на, что похожи коэффициенты этого уравнения? Правильно на дату.

Ребята, откройте тетради, запишите число и отложите тетради. У вас на столе лежат карты результативности, в которые вы будете вносить свои результаты в течение урока.

Итак, на доске у нас квадратное уравнение.

Давайте  вспомним, а что мы знаем о квадратных уравнениях. Я предлагаю вам поделиться на 2 группы. Каждая группа составит свой кластер.

Молодцы.

Постановка целей и задач. Мотивация учебной деятельности учащихся (1 минута).

Ну что ж, проверка показала, что повторение не будет лишним для нас с вами. Оскар Уайльд сказал: «Любовь живёт повторением, а повторение превращает её в искусство».  Предлагаю применить эту цитату к математике. Давайте попробуем превратить ранее полученное знание в искусство. Цель нашего урока: повторение, актуализация и систематизация знаний и умений по теме «Квадратные уравнения». Слайд.1,2

3. Актуализация изученного материала. БЛИЦ - ОПРОС:

По одному члену из каждой группы отвечают на вопросы. Группа может помогать.

- Какое же уравнение называется квадратным уравнением?

(ах²+ вх + с =0)

- Как называются числа а, в и с в квадратном уравнении? (старший коэффициент, второй коэффициент, свободный член)

- А как  называется уравнение, у которого старший коэффициент равен1?.(приведенным)

-Как называются квадратные  уравнения, у которых  хотя бы один из коэффициентов в или с =0  (неполное)

- Что  необходимо найти, чтобы решить  уравнение  ? (дискриминант).

-.Какие формулы для его нахождения вам известны? Молодцы! Вспомнили.

2. Самостоятельная работа.

- Я предлагаю вам поиграть, как в детстве в игру «Найди лишнее». Вам предстоит в каждой группе уравнений выбрать лишнее и объяснить свой выбор (слайд)

.

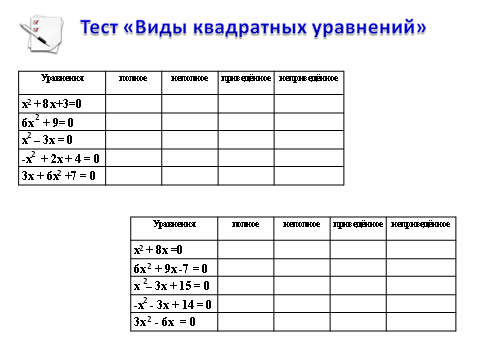
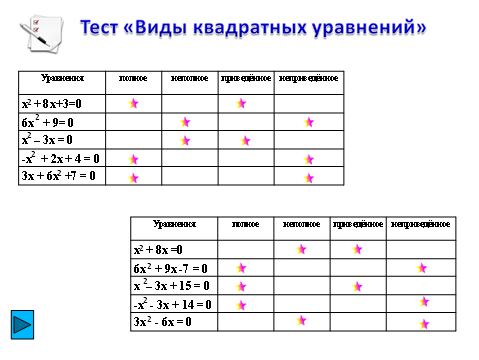
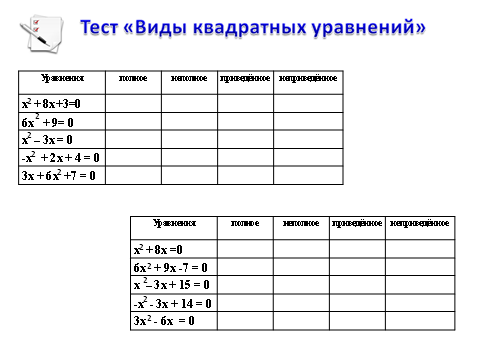
-Теперь давайте проверим, насколько хорошо вы умеете определять виды квадратных уравнений. Вашему вниманию предлагается тест,  в котором нужно определить вид пяти предлагаемых уравнений. Напротив каждого уравнения вы ставите «плюс» в той колонке, какому виду оно принадлежит (слайд)

Написать на доске теорему Виета для приведенного и неприведенного квадратного уравнения.

 слайд.

Не решая уравнение,

Найдите:

а)     Сумму корней:

б)    Произведение корней:

в) Корни данного уравнения.

Молодцы! Вспомнили. Переходим к следующему этапу урока.

3. Буквоград. Проанализируйте высказывания. Зачеркните в таблице буквы, обозначающие ложные высказывания (номер высказывания совпадает с порядковым номером буквы). Из оставшихся букв получите слово.

1. Уравнение x²+9=0 имеет два корня.

2.В уравнении x²-2x+1=0 единственный корень.

3. В уравнении x²-5x+3=0 сумма корней равна - 5.

4. В уравнении x²+3x=0 один из корней – отрицательное число.

5. В уравнении x²=0 дискриминант равен 0.

6. Уравнение x²-8x-3=0 не имеет корней.

7. Корнями уравнения x²-100x+99=0 являются числа 99 и 1.

8. Произведение корней уравнения x²-11x+9=0 равно - 9.

9. Корни уравнения x² – 0,16 = 0 равны .?

10. Уравнение x²-9x+8=0 является неполным.

11. Если дискриминант уравнения – число отрицательное, то уравнение не имеет корней.

12. Корни уравнения x²-4х =0 являются противоположными числами.

13. Уравнение x² =0 имеет один корень.

В результате вычёркивания букв должно получиться: ОТЛИЧНО

4. этап урока.

А сейчас вы все испытаете на себе роль учителя. Перед вами лежат примеры решенных уравнений нерадивым учеником (карточка № 2). Вам нужно найти ошибки (если они есть) и исправить их. Работа в парах. Взаимопроверка.

1)           2)

3)

Все проверили данные уравнения? И выставили оценку ученику? Кто он - отличник или двоечник?

каждой группе было задано четыре уравнения. Сверим ответы. Внимание на экран! (слайд)

(На экране высвечиваются три группы уравнений с ответами)

А теперь каждый возьмите индивидуальную координатную плоскость и отметьте все найденные корни, как координаты точек, последовательно их соединяя. Последнюю точку соедините с первой. Справились? Что у вас получилось?

- Да, у вас получилась «пятерка» - любимая оценка всех учеников. Я надеюсь, что каждый из вас сегодня получит эту оценку за работу на уроке.

5. Решение задач

В начале урока  мы говорили , о том что каждому человеку  без знаний  математики в жизни не обойтись. И сегодня мы убедимся, что без умения решать квадратные уравнения, невозможна жизнь современного человека.

Наверное ,вы устали. Давайте немного отдохнем.

6) Физминутка

- Ребята, пришло время немного отдохнуть.

Закройте глаза, расслабьте тело,

Представьте, вы – птицы, вы вдруг полетели!

Теперь в океане дельфином плывете,

Теперь в саду яблоки спелые рвете.

Направо, налево, вокруг посмотрели…

Ну что, дорогие, снова за дело!

Молодцы! Вспомнили. Переходим к следующему этапу урока.

7) Из истории математики (слайд)

каждой группе было задано четыре уравнения. Сверим ответы. Внимание на экран! (слайд)

(На экране высвечиваются три группы уравнений с ответами)

А теперь каждый возьмите индивидуальную координатную плоскость и отметьте все найденные корни, как координаты точек, последовательно их соединяя. Последнюю точку соедините с первой. Справились? Что у вас получилось?

- Да, у вас получилась «пятерка» - любимая оценка всех учеников. Я надеюсь, что каждый из вас сегодня получит эту оценку за работу на уроке.

Ребята! Урок наш подходит к концу. Мне хочется еще раз убедиться, что вы все умеете решать квадратные уравнения. Я предлагаю вам выполнить такую работу. Каждой группе нужно решить по 6 уравнений , т.е. каждому из вас – по 2 уравнения. Корни уравнения – это координаты точек, отметив их и последовательно соединив, кроме последней в координатной плоскости ,вы должны  получить какую – то фигуру. Приступаем выполнять.

Рефлексия

Домашнее задание: составить пять квадратных уравнений

Оценочный лист ФИ___________________________________________________

Оценочный лист ФИ___________________________________________________