
Районная научно-практическая конференция школьников
«Перекрёстки открытий»
Секция МАТЕМАТИКА
«Математика в работах художника М. Эшера»
Автор: Гусейнова Диана, 12 лет
МАОУ СОШ № 3 г. Черепаново, 6 «В» класс
Научный руководитель: Миллер Анна Александровна
Учитель математики, высшая категория Контактный телефон руководителя: 8-961-980-0961
г. Черепаново 2019
Содержание Стр.
Введение………………………………..…….…..….……………....…..3
Глава1 О Маурице Эшере…………....………………..………………..5
Глава 2 Виды работ М. Эшера………………….……………..…….....9
Глава 3 Исследование математических закономерностей в работах М.
Эшера. Этапы создания мозаики…………………………………………..10
Заключение………………………………………………......................16
Список литературы……………………………………………….……18
Использованное оборудование
Приложение 1 «Рисунки М. Эшера в современности»
Приложение 2 «Некоторые работы М. Эшера»
Приложение 3 «Виды работ М. Эшера»
Приложение 4 «Рисунок из работы по кристаллографии»
«Наука и искусство так же связаны между собой, как сердце и
лёгкие...»
/Л. Толстой/
Ярким примером и подтверждением, на мой взгляд, данного высказывания является искусство голландского художника Маурица Корнелиуса Эшера. Его творчество настолько необычайно, что мне захотелось разобраться и понять секреты некоторых его произведений. Поскольку я люблю рисовать и посещаю кружок рисования, интересно было узнать, насколько математика может помочь в изобразительном искусстве, смогу ли я нарисовать свою мозаику, подобно мозаикам Эшера…?
Рассматривая работы М. Эшера, я поняла, что они уже встречались мне: рисунок на ткани, паркеты, иллюстрации в книгах. (Приложение 1). Необыкновенные рисунки, создание которых, до сих пор привлекают внимание настоящих ценителей прекрасного. Картины М.Эшера настолько разнообразны, что в рамках одного исследования невозможно всё рассмотреть, поэтому я остановилась на мозаиках, т.к. именно их мне захотелось нарисовать. Но не разобравшись с принципом построения мозаики, её нарисовать оказалось сложной задачей. Поэтому пришлось познакомиться с некоторыми математическими понятиями.
Считаю её актуальной по нескольким причинам:
- поняв законы, по которым созданы картины, можно применять их при создании собственных изобразительных произведений;
- знакомство с творчеством выдающихся, талантливых людей побуждает к развитию собственных способностей;
-работы М. Эшера показывают привлекательность и увлекательность науки математики, а ещё точнее геометрии, которую мне предстоит изучать на следующий год.
Гипотеза:Предполагаю, что, мне удастся в работах Эшера найти математические закономерности и на их основе создать свой рисунок- мозаику.
Объект исследования: Работы Эшера.
Предмет исследования: Математика в работах Эшера.
Цель: Выявление математических основ некоторых произведений Эшера и создание собственного рисунка.
Задачи: 1. Познакомиться с творчеством Эшера
2. Изучить некоторые математические понятия, лежащие в основе его рисунков.
3. Создать собственную мозаику.
Методы: обобщение, сравнение, анализ
Мной были изучены электронные ресурсы по данной теме, а также книги в электронном варианте об этом художнике. Из учебника геометрии 7-9 класса я познакомилась с видами движения.
 Все
мои произведения – это игры.Серьезные игры.
Все
мои произведения – это игры.Серьезные игры.
М. К. Эшер
Мауриц Корнелис Эшер— голландский художник, не поддающийся классификации, любимец математиков, физиков и других людей науки за крайне нестандартное творчество. Первый из художников, кто смог хорошо изобразить бесконечность, рекурсию, перевёл математические абстрактные конструкции на язык графики.
Ни один художник не старался столь усердно, как М.К.Эшер, передать свои впечатления. Для него оболочка видимого мира была лишь кусочком ткани, которую можно самым чудесным образом резать, складывать, придавать ей любую форму. Рисовальщик, не знавший себе равных, он запечатлел эти странные преобразования пространства на листе бумаги, создав произведения, приводившие в восторг тысячи зрителей во всем мире.
[3]
Родился 17 июня 1898 года в Леевардене, административном центре голландской провинции Фрисландия. Он был третьим сыном инженера Г. А. Эшера и его второй жены, дочери министра. В доме, где родился Эшер, сейчас находится музей.
В 1903 году семья переехала в Арнем, там мальчик некоторое время учился столярному делу и музыке. В 1912-1918 годах он обучается в средней школе. Оценки по всем предметам у Маурица были плохими за исключением рисования. Учитель рисования заметил талант у мальчика и научил его делать гравюры по дереву.
В 1917 году семья Эшера переезжает в голландский город Остербек, расположенный в окрестностях Арнема. В 1918-1919 годах Эшер посещает Технический колледж в голландском городке Дельфт, но из-за слабого здоровья Мауриц не справился с учебным планом, и был отчислен. В результате, Эшер так и не смог получить высшее образование. Все еще в надежде получить диплом архитектора в 1919-1922 годах юный Эшер учится в Школе архитектуры и орнамента в городе Гаарлеме.
В начале 1920-х гг. Эшер часто путешествует в Италию. Именно там он впервые встречается с Джеттой Умикер, которая в 1924 году становится его женой. Чета жила в Риме до 1935 года, когда пребывание в Италии, под контролем режима Муссолини, стало для них невыносимым. Затем Эшеры переехали в Швейцарию. В январе 1941 года, после начала Второй мировой войны, Эшеры возвращаются в Нидерланды. С 1940-х по 1970-е они жили в голландском городе Барн (Baarn). Жена Эшера не была счастлива в Барне и в скорее в 1968 году вернулась в Швейцарию, где и провела остаток жизни. Эшер остался в Барне и погрузился в работу. И, хотя здоровье его ухудшалось, он продолжал создавать гравюры по дереву.
В 1970 году после новой серии операций Эшер переехал в новый дом в Ларене (Нидерланды), в котором была студия, но плохое здоровье не давало возможности много работать. Была издана книга о жизни и творчестве художника. Эшер прожил достаточно долго, чтобы увидеть книгу "Мир М. К. Эшера" (TheWorldof M. K. Escher) переведенную на английский язык и остался ею очень доволен. Последняя работа, законченная Эшером - "Змеи". В марте 1972 года самочувствие художника сильно ухудшилось. Вся семья собралась возле постели больного: 27 марта, в возрасте 73 лет, Мауриц Эшер - скончался.
Его литографии, гравюры на дереве можно увидеть в кабинетах математиков и других ученых во всех уголках мира. С середины прошлого века без его гравюр не обходится ни одна «иллюстрированная» книга по физике, математике, топологии, не говоря уж о популярных изданиях.
(Советский научно-популярный журнал «Квант» публиковал Эшера свыше
20 раз.) Например, учебники «Математика 10», «Математика 11» автор
Мордкович А. Г. В оформлении учебников использованы литографии Эшера, а также учебники геометрии Смирновых. Его имя можно встретить и в книгах по информатике. Можно увидеть галстуки, чашки, часы и красивые ткани, украшенные паркетами Эшера, футболки с рисунками орнаментов Эшера, фигурные элементы мощения – брусчатые камни.
В 1954 году в Амстердаме состоялась большая выставка Эшера, приуроченная и Международному математическому конгрессу. Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования. Однажды известный геометр Г.Кокстер пригласил Эшера на свою лекцию, посвященную математическому содержанию его гравюр и литографий. Ко взаимному разочарованию, Эшер не понял почти ни слова из того, о чём рассказывал Кокстер. Вот что писал об этом сам художник: "Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен".[3]
Некоторые факты о Маурице Эшере:
• Самая большая картина Маурица Эшера - "Метаморфозы-2", на которой представлена последовательность 10 трансформаций. Это полотно размером 19 см на 3,9 м. (Приложение № 2 рис 1)
• Однажды, чтобы найти средства на круиз по Средиземному морю, Эшер обратился в морскую компанию "Адрия". Он предложил гравюры кораблей и портов, которые сделает в пути, в качестве платы за путешествие. В "Адрии" с радостью согласились.
• Как и многие гении, Эшер был левшой. Он рисовал левой рукой, а писал правой.
• Знаменитую серию гравюр "Дни творения" Эшер создал после гибели брата-альпиниста. (Приложение № 2 рис 2)
• Художник был убежденным атеистом. Старинный шкаф, который остался после его смерти, был украшен фотографиями жены, сыновей, Эйнштейна и Анны Франк. А на полках шкафа стояли почитаемые им кристаллы.
• Когда Мик Джаггер обратился к Эшеру за разрешением поместить на обложку своего альбома гравюру "Вербум", Эшер ему отказал. Это, правда, не помешало другим многочисленным музыкантам без разрешения лепить рисунки Эшера на свои пластинки.
• Эшер иногда создает модели некоторых объектов для своих картин из глины, дерева, проволоки и других материалов.Создавая "Рептилий", Эшер сначала вылепил фигурку крокодила из пластилина и перемещал ее по столу. (Приложение № 2 рис 3)
• В наследии МаурицаЭшера 448 ксилографий, линогравюр и литографий и больше 2000 рисунков. Из них ровно 137 тесселляций. Тесселляция -- это мозаика из абсолютно одинаковых форм, которые прилегают друг к другу без промежутков и не перекрывая одна другую.
Все работы М. Эшера можно делить по разным признакам. Например сайт «Мауриц Корнелис Эшер» (http://mcesher.ru/) разделил работы следующим образом:
• Ранние работы (1916–1922)
• Итальянский период (1922–1935)
• Швейцария и Бельгия (1935–1941)
• Назад в Голландию (1941–1954)
• Успех и признание (1955–1972)
• Симметрия
• Магические кубики
В других источниках его картины разделены на следующие группы
• Мозаики
• Многогранники
• Форма пространства
• Логика пространства
• Геометрические парадоксы
• Самовоспроизведение и информация
• Спирали
В приложение № 3 представлены некоторые работы по каждой категории второй группы. В главе 3 я опишу математические закономерности, которые мне удалось обнаружить в работах только из раздела «Мозаики», а также некоторые приёмы, которые помогут создавать свои собственные мозаики.
М. Эшера.
Прежде чем искать математические закономерности в работах, я поговорила с учителем ИЗО школы искусств и спросила, рисовали ли учащиеся школы искусств рисунки подобные мозаикам Эшера и нужны ли знания математики, чтобы их рисовать. Она рассказала, что был опыт рисования, но рисунки были срисованы с работ Эшера, процесс был очень трудным, и теперь они не рисуют мозаики. Возможно, действительно необходимо опираться на знания математики, чтобы рисовать мозаики…?
Из толкового словаря Ожегова С.И. «мозаика – это узор из скреплённых друг с другом кусочков смальты, разноцветных камешков, эмали, дерева.», но в википедии я нашла, что «паркеты иначе называются замощениями, мозаиками (англ. tessellation, tiling), разбиениями плоскости
(англ. partition), паркетажами.» [6]
Паркет, прежде всего, это понятие математическое и связано непосредственно с геометрией на плоскости. Значит связь с математикой уже обнаружилась! Паркетом называют покрытие плоскости многоугольниками. Мозаика получается так же, как и паркет, замощением плоскости многоугольниками, но только различной, в том числе и неправильной, формы. При этом многоугольники выбираются из цветных материалов, в результате чего создаются разнообразные художественные произведения мирового уровня, ценность которых проверена веками.
Эшер интересовался всеми видами мозаик - регулярными и нерегулярными (прим. нерегулярные мозаики образуют неповторяющиеся узоры) - а также ввел собственный вид, который назвал "метаморфозами", где фигуры изменяются и взаимодействуют друг с другом, а иногда изменяют и саму плоскость. Интересоваться мозаиками Эшер начал в 1936 году во время путешествия по Испании. Он провел много времени в Альгамбре, зарисовывая арабские мозаики, и впоследствии сказал, что это было для него "богатейшим источником вдохновения". Но своим мозаикам он придавал облик животных, птиц, рыб.
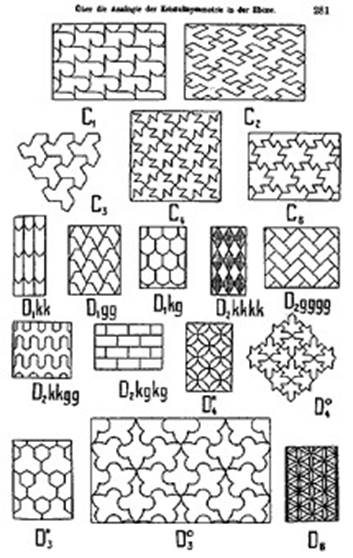
В процессе создания мозаик он черпал идеи из математических статьей, в которых рассказывалось о мозаичном разбиении плоскости. Многое он узнал, прочитав в 1937 году работу профессора Полии, посвященную кристаллографии. (рисунок из работы профессора Полии Приложение 4), в которой он неожиданно для себя нашел новый источник вдохновения. В 1958 году Эшер опубликовал свою книгу «Регулярное деление плоскости» (нидерл. Regelmatige vlakverdeling) К глубокому сожалению, эту книгу не удалось найти, но некоторые выдержки из книги представлены ниже:
"В математических работах регулярное разбиение плоскости рассматривается теоретически... Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней".

Рисунок из книги «Регулярное деление плоскости» М.Эшер.
Регулярное разбиение плоскости, называемое "мозаикой" - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Известно, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. (Нерегулярных вариантов разбиения плоскости гораздо больше.). Нет никаких других правильных плиток, потому что общие углы должны составлять в сумме 360 градусов. С правильными многоугольниками достичь этого можно тремя путями: использовать четыре квадрата, каждый с углами 90 градусов, три шестиугольника, каждый с углами 120 градусов, или шесть треугольников, каждый с углами 60 градусов. Главное требование заключается в том, что угол многоугольника составляет целое число и является делителем числа 360.
Эшер исказил базовые фигуры, превратив их в птиц, животных, ящериц и прочее, применял к ним трансформации (движения), которые в геометрии называются симметрией, поворотом, параллельным переносом
Ниже представлю некоторые работы Эшера и правильные многоугольники, которые, как я считаю, легли в основу рисунка.
 Квадрат
наполнился образом лягушки. Далее поворот на 900 относительно центра
квадрата и параллельный перенос на длину стороны квадрата.
Квадрат
наполнился образом лягушки. Далее поворот на 900 относительно центра
квадрата и параллельный перенос на длину стороны квадрата.

 «Бабочки»
Центральная симметрия, в которой перенос изображения осуществляется
относительно точки О. Следовательно, это произведение искусства Эшер создал как
раз, используя центральную симметрию.
«Бабочки»
Центральная симметрия, в которой перенос изображения осуществляется
относительно точки О. Следовательно, это произведение искусства Эшер создал как
раз, используя центральную симметрию.
 Кроме
того, Эшер стал изображать в своих мозаичных картинах фракталы (фигуры,
состоящие из собственных маленьких подобий) еще до того, как математический
термин «фрактал» был введен в употребление в 1975 году. Такое явление называют
рекурсией, при котором объект повторяет сам себя, иногда — бесконечно. Эшер много
раз использовал рекурсивный метод в разных формах.
Кроме
того, Эшер стал изображать в своих мозаичных картинах фракталы (фигуры,
состоящие из собственных маленьких подобий) еще до того, как математический
термин «фрактал» был введен в употребление в 1975 году. Такое явление называют
рекурсией, при котором объект повторяет сам себя, иногда — бесконечно. Эшер много
раз использовал рекурсивный метод в разных формах.
Ниже представлен фрагмент из книги Эшера.

Только после того, как мне удалось разобраться в этапах создания рисунков Эшера, я смогла изобразить что-то своё. Оказалось очень сложно не только математически понять как получаются эти рисунки, но и наполнить своим содержанием. Ещё один важный момент для построения мозаики: если какой-то кусочек из базовой фигуры убирается, то такой же должен появится, либо смещённый параллельно, либо поворотом относительно вершины.
Приведу пример получения мозаики:
1
 За основу взяла квадрат, несложное преобразование и
параллельный перенос. Затем придумывался образ для полученной формы.
За основу взяла квадрат, несложное преобразование и
параллельный перенос. Затем придумывался образ для полученной формы.
2 За основу взяла квадрат. Трансформация путём поворота вокруг противоположных вершин. В этом случае мозаика собирается поворотом.
 Части, которые
трансформировала закрепила скотчем.
Части, которые
трансформировала закрепила скотчем.
Обвела, путём поворота.
Придумала образ. На примере этой мозаики можно увидеть
геометрические преобразования: поворот, центральная симметрия.
Далее возникла идея собрать этот рисунок как настоящую мозаику. Я перенесла образ на лист А4. Сфотографировала и с помощью компьютера в обычном текстовом редакторе размножила, перекрасив несколько в тёмный цвет. Далее распечатала, вырезала и склеила мозаику.

Вывод: Т.о. действительно, в произведениях Эшера из раздела «Мозаики» можно читать математические закономерности. Начиная от разбиения плоскости и заканчивая наполнением взаимосвязанных изображений птиц, животных, расположенных согласно законам симметрии, параллельного переноса, поворота. Удивительно, но сам Эшер не считал себя человеком, знающим математику… Наверно он просто был гений, фантастический человек с нестандартным мышлением и видением мира. Но его работы действительно могут помочь в изучении математики. Думаю, не зря, учебник геометрии И.М. Смирнова и В.А. Смирнов наполнены его рисунками.
Творчество Эшера оказало огромное влияние на большое количество художников в разных странах мира. Работы Эшера являются наиболее излюбленными среди математиков, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов.
Чтобы сделать работы интересными, мастер часто скрывал основной геометрический образец, стыкуя различные формы и цвета. Каждый из образцов — шарада, загадка. Иногда невозможно угадать, какова форма основы рисунка.

Американский математик Дорис Шатчнейдер, исследуя записи Эшера, пришел к выводу, что тот создал собственную математическую систему для классификации изразцов. Он использовал специальные символы для описания того, как состыковать их между собой. Система позволила ему найти множество способов для скрепления самых невероятных форм, которые, казалось бы, по всем математическим канонам нельзя соединить воедино. Он пытался в своих гравюрах показать, что мы живем в прекрасном и упорядоченном мире, а не в бесформенном хаосе, как иногда кажется. Его работы – мост между наукой и искусством. Он получал удовольствие, смешивая двух- и трехмерность, плоскость и пространство, смеясь над гравитацией.
Над секретом Эшера до сих пор ломают головы дизайнеры всего мира. Однако пока еще никому не удалось до конца разгадать тайну гениального художника. Современные бизнесмены делают хорошие деньги на имени Мориса Эшера, продавая товары с использованием его мозаических рисунков. Так же можно приобрести большое количество ребусов и головоломок на основе его замысловатых узоров. Его мотивы встречаются в оформлении комнат, тканей, элементов одежды и аксессуаров. Очень многие графические находки Эшера вошли в число символов XX века и часто «цитируются» другими художниками.
Воспользовавшись советами по составлению мозаики, можно самим нарисовать свой мозаичный рисунок. У меня это получилось. Эти рисунки в дальнейшем можно использовать в оформлении интерьера. Получится отличная дизайнерская разработка.
Моя гипотеза подтвердилась. В работе я представила произведения художника разных лет, провела исследование и доказала, что в своих рисунках М.Эшер применял различные виды симметрии, параллельного переноса, поворота.
Данная работа дала мне возможность познакомиться с творчеством интересного человека, который вдохновляет мыслить. Я узнала многое о разных видах движения (симметрия, перенос, поворот и др.) На моих рисунках также можно видеть законы математики (симметрия, поворот, параллельный перенос). И самое главное я поняла, что и геометрия помогает в создании красоты и удобства, уюта т.е. того что объединяем одним словом – гармония!
Хотя Эшер не много не дожил до компьютерной революции, но своими работами он доказал, что предвидел компьютерную графику. Изучая информатику в старших классах, возможно я попробую создать мозаики с помощью компьютерных программ.
1. Дорофеев С.Н. Геометрические преобразования в примерах и задачах:
Учебное пособие. – Пенза: Информационно-издательский центр ПГУ, 2002. – 189c.
2. Левитин К.Е. Геометрическая рапсодия — 3-е изд., перераб. и доп. — М.: ИД «Камерон», 2004. — 216 с, с ил.
3. Лошер Ж. Л., Вельдхуизен В. Ф. Магия М. К. Эшера. — Арт-Родник, Taschen, 2007.
4. Новое время, №36, 1998. Зайцева Е. «Творец невозможного: художественные образы математика Мариуца Эшера.»
5. Студенческий меридиан № 05, 2008. загадка остается загадкой
«ЭШЕР: ТАЙНА НЕОКОНЧЕННОГО РИСУНКА»
6. Википедия. Паркеты. Электрон. данные.-Режим доступа:
https://ru.wikipedia.org/wiki/Замощение_(геометрия)(26.02.2019) 7. Геометрия 7-9 классы: учебник для общеобразовательных учереждений/ И.М. Смирнова, В.А. Смирнов – 7-е изд., стер. – М.:
Мнемозина, 2013. – 376с.:ил.
Использованное оборудование
Компьютер, принтер
Рисунки Эшера в современности.


 рис. 1
«Метаморфозы -2» рис. 2 из серии гравюр "Дни творения".
рис. 1
«Метаморфозы -2» рис. 2 из серии гравюр "Дни творения".

рис. 3 «Рептилии»
• Мозаики

• Многогранники

Порядок и хаос. 1950, литография Звезды. 1948, резьба по дереву
• Форма пространства

Три пересекающиеся плоскости, литографияГалерея. 1956, литография


Змеи. 1969, гравюра на деревеВсадник. 1946, гравюра на дереве
• Логика пространства

 Вверх и вниз. 1947, литография Куб
с полосками
Вверх и вниз. 1947, литография Куб
с полосками  Водопад. 1961, литография
Водопад. 1961, литография
• Геометрические парадоксы


Относительность. 1953, литография Выпуклые и вогнутые. 1955, литография
 Бельведер. 1958, литография
Бельведер. 1958, литография
• Самовоспроизведение и информация
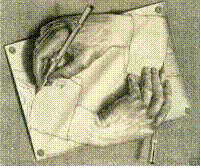
Рисующие руки. 1948, литография

Циклический предел II. 1959, гравюра на дереве
•

 Спирали
Спирали
Сферическая спираль. 1958, гравюра на дереве Кожура.
 1955, резьба по дереву и гравюра на дереве
1955, резьба по дереву и гравюра на дереве
Спирали. 1953, резьба по дереву
Рисунок из работы профессора Полии по кристаллографии.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.