Математика в жизни пчел

Содержание

Введение

Я всегда задавала себе вопросы: а зачем изучать тот или иной предмет в школе, а в частности – математику? А где  и как математические  знания применяются в жизни? Я решила расспросить своих одноклассников, которые утверждали, что эта наука им нужна для будущей профессии. Но моё мнение следующее: всё, что нас окружает,  подчиняется математическим законам. Даже насекомые в своей жизни пользуются ими.

Актуальность данной работы заключается в следующем:

использование в жизнедеятельности человека математического опыта других живых организмов (на примере пчел).

Цель работы: показать, как применяют  пчелы  в  своей  жизни      

                          математику.

Задачи:

1.     Изучить литературу.

2.     Провести опрос – анкетирование.

3.     Взять интервью у пчеловода.

4.     Сделать модели пчелиных сот.

5.     Выполнить расчеты.

6.     Сделать вывод.

Методы исследования:

ü Изучение литературы.

ü Опрос.

ü Интервью с опытными пчеловодами.

ü Расчеты.

Предыстория «Как я пришла к теме исследовательской работы»

Однажды  делая домашнюю работу по математике, я почувствовала, что у меня началась простуда. А чем её лечат? Конечно, горячим чаем с лимоном и мёдом! Тем более, что мой дядя – настоящий пчеловод, очень много мне рассказывал интересного о пчелах, показывал пчелиные соты. Тогда я задумалась: а как пчелы выбирают, с каких цветов собирать нектар, а с какой скоростью они  летают, а почему соты именно такой формы?

Глава 1. Общая информация  по теме исследования

Изучение литературы

В процессе изучения литературы  и электронных источников я узнала много интересного из жизни пчел и отметила для себя самое главное:

пчелы – уникальные медоносные насекомые, которые поражают своей выносливостью и работоспособностью, могут облететь максимум  цветов за минимум времени, найти оптимальный путь от одного к другому, рой пчел стремится принять форму шара, ячейки пчелиных сот представляют собой правильные шестиугольники.

Опрос

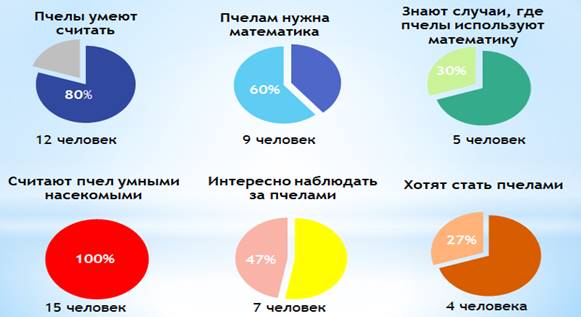
Я провела анкетирование своих родственников, задавая им следующие вопросы:

1. Умеют ли пчелы считать?

2. Нужна ли пчелам математика?

3. Знаете ли Вы, в каких случаях пчелы используют математику?

4. Считаете ли вы пчел – умными насекомыми?

5. Интересно ли было бы Вам понаблюдать за пчелами?

6. Хотели бы Вы стать пчелой?

По итогам опроса получила следующие результаты:

Интервью с опытным пчеловодом

Продолжая свою исследовательскую деятельность, я взяла интервью у опытного пчеловода.

Вопрос 1: Почему пчелы принимают часто форму шара, например,  при перелете или когда роятся около ульев или на ветвях?

Ответ: «С такой формой пчёлам теплее и меньше требуется питания. Это очень актуально зимой или ранней весной. Летом - вентиляция»

Вопрос 2: Как далеко улетает пчела от улья во время медосбора?

Ответ: «Дальность полёта пчелы - не более 2-2.5 км. Если и на этом расстоянии мало нектара, то пчела может летать и на 3.5 км. Чем дальше летает пчела, тем меньше нектара она приносит.  За день пчела пролетает около 40-80 км. За время своей жизни пчела может пролететь около 10 000 км»

Вопрос 3: На какой высоте летают пчелы?

Ответ: «Высота полета пчелы обычно 10-12 м, а при ветре - 1 м от земли. Это связано с воздушными течениями и порывами ветра, возможными на такой высоте»

Вопрос 4: Почему не выливается мед из сот?

Ответ: «Ячейки сот расположены не перпендикулярно основанию, а под углом к ним. Этот угол направлен вверх. Именно такая конструкция ячейки позволяет складировать мёд и постепенно запечатывать его, не допуская вытекания»

Вопрос 5: Всегда ли у пчел соты в виде шестиугольников?

Ответ: «Да. Пчелы строят стенки ячеек сот и утрамбовывают мед именно в шестиугольные соты. Так пчелы экономят пространство и воск»

Глава 2. Практическая часть исследования

Основной вопрос исследования:

Почему пчелы выбрали для своих сот именно шестиугольник?

ИССЛЕДОВАНИЕ

1) Пчелиные соты представляют собой прямоугольник, покрытый правильными шестиугольниками. Проведём исследование следующего вопроса: какими еще правильными многоугольниками можно покрыть плоскость прямоугольника.

У каждой фигуры выберем одну из вершин, которая будет общей.

Применим «Метод перебора».

Для треугольника. Три угла, плотно составленные, образуют 180°, а шесть углов - 360°. Плоскость покрыта без просветов.

Для квадрата. Четыре внутренних угла вместе дают 360°. Плоскость покрыта без просветов.

Для пятиугольника. Внутренний угол правильного многоугольника равен 180°, остается просвет в 36°. Плоскость без просветов не покрывается.

Для шестиугольника.  Внутренний угол правильного шестиугольника равен 120°, три шестиугольника, составленные вместе, образуют 360°. Плоскость покрывается без просветов.

   Для семиугольника. Три семиугольника не могут покрыть плоскость без просветов и не могут образовать вместе угол 360°.

Вывод: метод перебора можно продолжать и дальше, но уже понятно, что плоскость без просветов можно покрыть лишь правильными треугольниками, квадратами и  шестиугольниками.

2) Сравним периметры правильного треугольника, квадрата и  шестиугольника.

Пусть  S - площадь каждой из названных фигур равна 1 кв. ед.

Вычислим стороны и периметры многоугольников.

Для треугольника: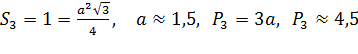  

Для квадрата:

Для шестиугольника: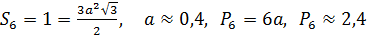

 Мы видим, что из трех правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник.

Стало быть, мудрые пчелы, экономят воск и время для построения сот.

3) Соты, в которых пчелы хранят золотистый нектар — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и как-то координируют свои попытки сделать соты одинаковыми.

Поэтому я выполнила модель пчелиной соты в трех видах, когда в основании треугольник, квадрат и шестиугольник. И проверю с помощью математических расчетов,  какая модель будет иметь наибольший объём.

Для исследования возьмем диаметр соты, равный 6 мм, тогда сторона шестиугольника будет равна 3 мм. Увеличу для построения моделей размеры в 15 раз, получу, что надо сделать модели,  в основании которых будут правильные многоугольники со стороной 4,5 см. Высотой 15 см, так как из литературы по пчеловодству – глубина соты 11-12 мм, округлю до 10 мм.

Итак, если в основании

треугольник: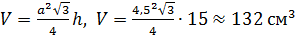  

квадрат:

шестиугольник: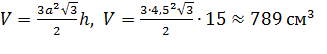

Итак, делаю вывод: пчелиная сота имеет именно такую геометрическую форму (шестиугольная правильная призма), чтобы был наибольший объём.

Глава 3. Результаты исследования

По итогам своего исследования я получила следующие результаты:

1.     Пчелы – талантливые математики.

2.     Математика присутствует во всех сферах жизни пчел.

3.     Шестиугольные соты – уникальное сооружение пчел.

4.     Математический опыт пчел используется человечеством.

Подробнее хочется еще остановиться на том, как математический опыт пчел используется человечеством:

·     в сотовой связи - мобильные вышки строят таким образом, что покрытие поверхности, то есть расстояние,  на которое передается сигнал, происходит в виде правильных шестиугольников – сот;

·     в архитектуре:

- в нью-йоркском Хадсон-Ярдс открылось общественное пространство Vessel, которое стало украшением площади на Манхэттене,  и новой визитной карточкой района;

- профессиональный учебный Центр в Эстонии, город Валга: фасад сконструирован в виде ярко-жёлтых и оранжевых «пчелиных сот» – шестиугольников правильной формы;

·      в авиастроении используются панели со структурой в виде сот. Самолеты, изготовленные из таких конструкций, обладают большей прочностью и легкостью, что снижает расход топлива;

·     в транспортной отрасли - при расчете минимального пути от одного объекта до другого.

Заключение

Еще много интересного из жизни пчел можно исследовать с помощью математики, но это уже другая исследовательская работа. Пока я понимаю, что мне не хватает знаний и математических умений (расчеты помогла сделать руководитель – учитель математики).  Но в будущем, думаю, что продолжу исследование жизни пчел – этих уникальных созданий природы, а математика в этом мне поможет.

Список используемых источников и литературы

Электронные ресурсы:

1.     Портал «Мед во благо». Статья «Почему пчелы строят шестигранные соты».

2.     URL: https://medvoblago.ru/pchelovodstvo/pochemu-soty-pchel-imeyut-shestigrannuyu-formu/

3.     Портал «Вокруг нас». Статья «Пчелы и математика: являются ли данные насекомые математически одаренными?»

4.     URL: https://vokrug-nas.ru/pchely-i-matematika-yavlyayutsya-li-dannye-nasekomye-matematicheski-odarennymi/ 

5.     Портал «У пчел» URL: https://upchel.ru/pchelovodstvo/o-pchelah

6.     Портал «Теория и практика». Статья «Пчелиная экономия: почему природа предпочитает шестиугольники?» URL: https://vokrug-nas.ru/pchely-i-matematika-yavlyayutsya-li-dannye-nasekomye-matematicheski-odarennymi/ 

7.     https://www.google.com/search?sxsrf=ACYBGNRON52Jns8RfjID9nAmEUhZGyHqVw:1576097667784&q=%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B0+%D0%BF%D1%87%D0%B5%D0%BB%D0%B8%D0%BD%D0%BE%D0%B9+%D1%81%D0%BE%D1%82%D1%8B+%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9&tbm=isch&source=univ&sa=X&ved=2ahUKEwjRhvqsva7mAhWvy6YKHRZyC3cQsAR6BAgKEAE&biw=1366&bih=657#imgrc=RRtNB214GVZ9MM&imgdii=artK6xFVo36TeM

8.     https://www.google.com/search?q=%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B0+%D0%BF%D1%80%D0%B8%D0%B7%D0%BC%D1%8B&tbm=isch&ved=2ahUKEwji7q2uva7mAhWGwcQBHfUoA9QQ2-cCegQIABAA&oq=%D0%9A%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B0+%D0%BF%D1%80%D0%B8%D0%B7%D0%BC&gs_l=img.1.0.0j0i8i30.690634.696709..699149...1.0..1.138.1678.19j3......0....1..gws-wiz-img.......35i39j0i131.ODlFnvn5byk&ei=hlfxXeKTLIaDk74P9dGMoA0&bih=657&biw=1366#imgrc=v2bVQBNKCUNxLM

9.     https://www.google.com/search?q=%D0%A1%D0%BE%D0%BE%D1%80%D1%83%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F+%D0%BA%D0%B0%D0%BA+%D0%BF%D1%87%D0%B5%D0%BB%D0%B8%D0%BD%D1%8B%D0%B5+%D1%81%D0%BE%D1%82%D1%8B&tbm=isch&ved=2ahUKEwjdo-L8v67mAhXUapoKHY3BCy8Q2-cCegQIABAA&oq=%D0%A1%D0%BE%D0%BE%D1%80%D1%83%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F+%D0%BA%D0%B0%D0%BA+%D0%BF%D1%87%D0%B5%D0%BB%D0%B8%D0%BD%D1%8B%D0%B5+%D1%81%D0%BE%D1%82%D1%8B&gs_l=img.3...406434.419188..420304...1.0..2.239.3582.31j10j1......0....1..gws-wiz-img.....10..35i39j0i8i30j35i362i39j0i131j0j0i67j0i24j0i5i30._Oh5X3_j5_Q&ei=RFrxXd3xAdTV6QSNg6_4Ag&bih=657&biw=1366#imgrc=dx3CJZ4yuQKTCM&imgdii=Rm0QyOZo1AhlxM

10. https://www.google.com/search?q=%D0%A1%D0%BE%D0%BE%D1%80%D1%83%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F+%D0%BA%D0%B0%D0%BA+%D0%BF%D1%87%D0%B5%D0%BB%D0%B8%D0%BD%D1%8B%D0%B5+%D1%81%D0%BE%D1%82%D1%8B&tbm=isch&ved=2ahUKEwjdo-L8v67mAhXUapoKHY3BCy8Q2-cCegQIABAA&oq=%D0%A1%D0%BE%D0%BE%D1%80%D1%83%D0%B6%D0%B5%D0%BD%D0%B8%D1%8F+%D0%BA%D0%B0%D0%BA+%D0%BF%D1%87%D0%B5%D0%BB%D0%B8%D0%BD%D1%8B%D0%B5+%D1%81%D0%BE%D1%82%D1%8B&gs_l=img.3...406434.419188..420304...1.0..2.239.3582.31j10j1......0....1..gws-wiz-img.....10..35i39j0i8i30j35i362i39j0i131j0j0i67j0i24j0i5i30._Oh5X3_j5_Q&ei=RFrxXd3xAdTV6QSNg6_4Ag&bih=657&biw=1366#imgrc=MU8GO_jb9tk4dM&imgdii=1XfuyIdzMwCOzM

11. https://www.arhinovosti.ru/2014/08/04/medo vye-soty-v-arkhitekture-ehstonskojj-shkoly/

Литература:

12.  Н.Н. Зарецкий Уход за пчелами / Н.Н. Зарецкий. - М.: Россельхозиздат, 1981, 882 с

Скачано с www.znanio.ru