Сложение чисел с помощью координатной прямой. Правила

Вычитание целых чисел на координатной прямой

Осталось выяснить геометрический смысл вычитания целых чисел. В этом нам поможет координатная прямая, расположим ее горизонтально и направим вправо.

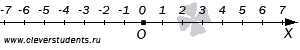
В предыдущих пунктах мы узнали, что вычитание из целого числа a целого числа b – это прибавление к числу a числа −b, то есть, a−b=a+(−b). Таким образом, геометрический смысл вычитания целых чисел a и b совпадает с геометрическим смыслом сложения целых чисел a и −b.

Отсюда следует, что при вычитании из целого числа a целого числа b нужно:

·         переместиться из точки с координатой a на b единичных отрезков влево, если b– положительное число;

·         переместиться из точки с координатой a на  ( - это модуль числа b) единичных отрезков вправо, если b – отрицательное число;

·         остаться в точке с координатой a, если b=0.

Приведем примеры и графические иллюстрации.

Вычтем на координатной прямой из целого числа −2 целое положительное число 2. Для этого из точки с координатой −2 нужно переместиться влево на 2 единичных отрезка. При этом мы попадем в точку с координатой −4, то есть, −2−2=−4.

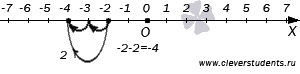
Теперь покажем на координатной прямой как проводится вычитание из целого числа 2 целого отрицательного числа −3. Мы из точки с координатой 2 перемещаемся вправо на  единичных отрезка, в результате чего попадаем в точку с координатой 5. Таким образом, мы проиллюстрировали равенство 2−(−3)=5.

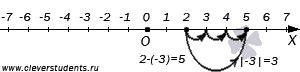
Скачано с www.znanio.ru