Математика_6кл_Понятие рационального числа_Приложение_1

Приложение 1

Теоретический материал

Числа – это ин­стру­мент, ко­то­рые че­ло­век со­зда­вал по мере необ­хо­ди­мо­сти. По­на­до­би­лось счи­тать пред­ме­ты или ну­ме­ро­вать их – по­яви­лись на­ту­раль­ные числа (Даль­ше, когда по­на­до­би­лось вести де­неж­ные рас­че­ты, перед чис­лом стали ста­вить знаки плюс или минус, по­ка­зы­вая, нужно уве­ли­чить или умень­шить ис­ход­ную ве­ли­чи­ну. Так по­яви­лись от­ри­ца­тель­ные и по­ло­жи­тель­ные числа. Новое мно­же­ство на­зва­ли мно­же­ством целых чисел ().

Счи­тать нужно не толь­ко целые ко­ли­че­ства, но и дроб­ные: на­при­мер,  литра воды По­это­му по­яв­ля­ет­ся новый ин­стру­мент, новые числа – дроби. Мы их за­пи­сы­ва­ем раз­ны­ми эк­ви­ва­лент­ны­ми спо­со­ба­ми: обык­но­вен­ны­ми и де­ся­тич­ны­ми дро­бя­ми ().

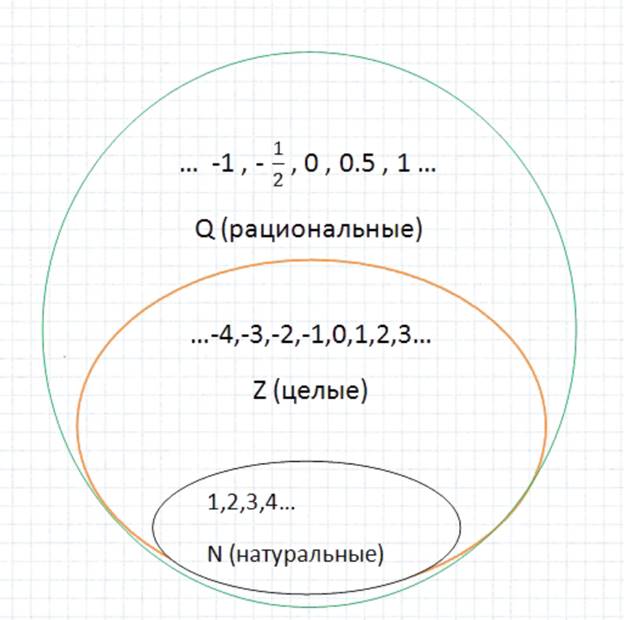
Все числа – «ста­рые» (целые) и «новые» (дроб­ные) – объ­еди­ни­ли в одно мно­же­ство и на­зва­ли его мно­же­ством ра­ци­о­наль­ных чисел ( – ра­ци­о­наль­ные числа )

Итак, ра­ци­о­наль­ное число – это число, ко­то­рое можно пред­ста­вить в виде обык­но­вен­ной дроби. Но это опре­де­ле­ние в ма­те­ма­ти­ке еще немно­го уточ­ня­ют. Любое ра­ци­о­наль­ное число можно пред­ста­вить в виде дроби с по­ло­жи­тель­ным зна­ме­на­те­лем, то есть от­но­ше­ни­ем це­ло­го числа к на­ту­раль­но­му: .

Тогда по­лу­ча­ем опре­де­ле­ние: число на­зы­ва­ет­ся ра­ци­о­наль­ным, если его можно пред­ста­вить в виде дроби с целым чис­ли­те­лем и на­ту­раль­ным зна­ме­на­те­лем ().

Итак, любое ра­ци­о­наль­ное число можно пред­ста­вить в виде обык­но­вен­ной дроби. Это его опре­де­ле­ние.

А любую обык­но­вен­ную дробь можно пред­ста­вить в виде ко­неч­ной или бес­ко­неч­ной пе­ри­о­ди­че­ской де­ся­тич­ной дроби.

Виды за­пи­си дро­бей:

за­пись де­ся­тич­ной дроби в виде обык­но­вен­ной: ; ;

за­пись обык­но­вен­ной дроби в виде де­ся­тич­ной:  (ко­неч­ная дробь);  (бес­ко­неч­ная пе­ри­о­ди­че­ская).

То есть любое ра­ци­о­наль­ное число можно за­пи­сать ко­неч­ной или пе­ри­о­ди­че­ской де­ся­тич­ной дро­бью. При этом ко­неч­ную дробь тоже можно счи­тать пе­ри­о­ди­че­ской с пе­ри­о­дом ноль.

Ино­гда ра­ци­о­наль­но­му числу дают имен­но такое опре­де­ле­ние: ра­ци­о­наль­ное число – это число, ко­то­рое можно за­пи­сать пе­ри­о­ди­че­ской де­ся­тич­ной дро­бью.