Математика в живописи Леонардо до Винчи. Доклад

Симметрия в природе

План:

I.       Введение.

II.    О сходствах и общих чертах в явлениях природы.

III.                        Учение о симметрии:

a.                  определение;

b.                 операция симметрии;

c.                  оси симметрии;

d.                 самосовмещение;

e.                  симметрии многогранников;

f.                   симметрия шара.

IV. Плоскость скользящего отражения:

a.                  О бесконечных фигурах в природе;

b.                 Трансляция как элемент симметрии;

c.                  Плоскость скользящего отражения;

d.                 Винтовая ось;

V.    Симметрия подобия;

VI. Геометрия в лесу:

a.                  «билатеральная» симметрия;

b.                 плоскость симметрии;

c.                  веер плоскостей.

VII.                     Вывод.

Литература:

a.                  И.И. Шафрановский. Симметрия в природе. Ленинград
                      «Недра», 1985 г.

b.                 Детская энциклопедия № 3

В старых учебниках географии изображались зонтикообразные итальянские сосны-пинии на фоне дымящегося Везувия. Зловещее облако после взрыва ядерной бомбы неспроста называют «атомным грибом», оно и в самом деле похоже по форме на самый обыкновенный безобидный гриб.
Струя фонтана напоминает куст или плакучую иву. Случайно ли это? И растущее дерево, и пары Везувия, и атомный простой гриб, и фонтан – все они с той или иной мощью и быстротой устремляются вверх до тех пор, пока сила земного тяготения не остановит их движения и не заставит обратиться вспять к земле. Действие силы тяготения сказывается, конечно, на всех телах, формирующихся в поле его влияния, как на безжизненных, так и живых. Совершим небольшую прогулку в чащу леса. Искривленные сучья, древние корявые стволы, тысячи разнообразных ветвей и листьев – можно ли в этом хаосе найти какие-то геометрические закономерности?

Непогрешимо строгую геометрию находим мы здесь: разве не является общим законом то, что деревья тянутся вверх, образуя вертикальные стволы. Или обыкновенный листок. Форма его не случайна. Она строго закономерна. Листок как бы склеен из двух более или менее одинаковых половинок. Одна из них расположена зеркально относительно другой.
 Плоскость, разделяющая листок на две зеркально равные части, называется плоскостью симметрии. Ботаники и зоологи называют симметрию листка «билатеральной», в переводе с латинского – дважды боковой. Только ли древесный листок обладает такой симметрией. Возьмем гусеницу. Мысленно мы ее можем разделить вдоль на две зеркально равные части. Или бабочка. Она тоже состоит из двух одинаковых половинок. Даже пятнистый узор на ее крыльях послушно подчиняется такой геометрии.

Итак, повсюду мы наталкиваемся на одно и то же. Везде упорно повторяется симметрия листка. Не удалось ли нам открыть универсальный закон, охватывающий все живое. Может быть, любое существо обладает плоскостью симметрии и подходит тем самым, под симметрию листка? Нет, с этим спешить нельзя. Возьмем хотя бы ромашку, сорвем и разглядим ее. Вокруг оранжевой середки расположены белые лепестки. Без всякого труда, можно ее разрезать на две зеркально равные половинки по линии, проходящей через центр цветка, и продолжающейся вдоль середины любого из лепестков или между ними. Однако, лепестков много, и вдоль каждого можно обнаружить плоскость симметрии. Значит, этот цветок обладает многими плоскостями симметрии, и все они пересекаются в его центре. Это уже целый веер или пучок пересекающихся плоскостей симметрии. Сходным образом можно охарактеризовать геометрию подсолнечника, василька, колокольчика.

Вернемся домой, и возьмем деревянный грибок, и на его модели попробуем разобраться с вопросами симметрии. Легко понять, что вдоль ножки и через середину шляпки можно провести бесчисленное множество плоскостей симметрии. Все они пересекаются в центре шляпки, образуя веер плоскостей. Следовательно, грибная симметрия родственна симметрии ромашки. У ботаников и зоологов такая симметрия называется лучевой или радиальной. Типичной радиально-лучевой симметрией обладают конусовидные ели, веретенообразные тополя, кипарис. Таких примеров в природе можно привести множество.

Итак, два вида симметрии с необычным упорством покоряются вокруг нас: билатеральная – симметрия листка, радиально–лучевая.  Очень важно отметить, что на не сорванных цветах и грибах, растущих деревьях, бьющем фонтане или столбе паров, плоскости симметрии ориентированны всегда вертикально. Выразим в упрощенном и схематизированном виде общий закон, ярко и повсеместно проявляющийся в природе: все, что растет или движется по вертикали, т.е. вверх или вниз относительно земной поверхности, подчиняется радиально-лучевой («ромашково-грибной») симметрии в виде веера пересекающихся плоскостей. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, подчиняется билатеральной симметрии (одна плоскость симметрии).

Наша цель – познакомиться с геометрическими законами, характеризующими формы природных тел. Для этого обратимся к основам учения о симметрии. Именно симметрия позволит охватить самые разнообразные тела с единых геометрических позиций. Слово симметрия в переводе с греческого означает «соразмерность». Своим развитием чисто геометрическое учение о симметрии обязано естествоиспытателям, углубленно изучавшим кристаллические  образования. Объясняется это тем, что формы кристаллов с древнейших времен поражали глаз своей симметричностью.

История науки показывает, что учение о симметрии развивалось крайне медленно и трудно. Поражающе правильные очертания кристаллов вызывали в древности суеверные представления. «Такое могли сотворить только ангелы или подземные духи», - утверждали наши предки, не догадываясь о том, что кристаллы растут в природе сами собой из растворов, расплавов, паров и в твердых каменных породах.

Перейдем к знакомству с научными, строго математическими понятиями, относящимися к симметрии.

1.                  Определение. Фигура называется симметричной, если она состоит из равных, закономерно повторяющихся частей. Понятие равенства фигур знакомо нам из курса геометрии: совпадение при наложении.

2.                  Плоскость симметрии – такая плоскость, которая делит (как бы рассекает или разрезает) фигуру на две зеркально равные части, расположенные друг относительно друг так, как предмет и его зеркальное отражение.

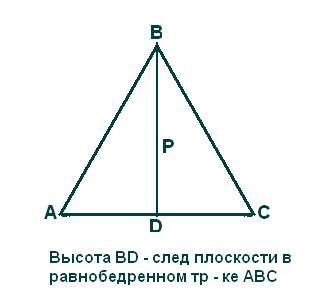Этот элемент симметрии обозначается прописной латинской буквой Р (символика Германа-Могена). Сама плоскость симметрии обозначается строчной латинской буквой m (от французского слова miroir – зеркало).

3.                 Операции симметрии называется двустороннее отражение фигуры в плоскости симметрии. К операциям симметрии относятся и повороты фигур вокруг определенных прямых (осей), и отражения в особых точках. Ко всем таким операциям предъявляется основное требование: после их проведения отраженная или повернутая фигура должна занять в пространстве то же положение, которое она занимала до этих операций. При этом фигура совмещается сама с собой или фигура самосовмещается.

4.                 Ось симметрии – прямая линия, вокруг которой несколько раз повторяются равные части симметричной фигуры. Эти равные части расположены так, что после поворота вокруг оси на некоторый угол, фигура занимает в пространстве то же положение, которое она занимала и до поворота. Только на месте одних ее частей оказались другие равные им части. В результате фигура приходит в самосовмещение. Ось симметрии обозначается буквой L (число самосовмещения фигуры при ее повороте вокруг оси на 360 градусов называется порядком оси), ее порядок n маленькой цифрой, стоящей вслед за этой буквой. Например, L₃ обозначает ось симметрии третьего порядка.

5.                 Кроме фигур, характеризующихся наличием одной неповторяющейся оси симметрии L_n  существуют тела, в которых каждое направление, а следовательно, и каждая ось повторяется несколько раз, следуя законам симметрии. Примером являются многогранники. К ним относятся знаменитые тела Платона – выпуклые многогранники, отличающиеся тем, что их грани являются правильными многоугольниками:

a.                   Тетраэдр (четырехгранник);

b.                  Куб (шестигранник);

c.                   Октаэдр (восьмигранник);

d.                  Додекаэдр (двенадцатигранник);

e.                   Икосаэдр (двадцатигранник).

Древнегреческий философ Платон (427 – 347 г. до н.э.) придавал этим телам особые значения, считая их олицетворением четырех природных стихий: огонь– тетраэдр (одна из вершин всегда обращена вверх); земля – куб (наиболее устойчивое тело), воздуха– октаэдр, вода – икосаэдр (наиболее «катучее» тело); додекаэдр представлял собой образ всей Вселенной.

Виды симметрии, выведенные из тетраэдра, куба и октаэдра, имеют множество кристаллических форм – октаэдры алмаза, кубы поваренной соли.

6.                  К фигурам, обладающим симметрично равными осями причисляется шар. В шаре любой диаметр является осью симметрии бесконечного порядка. Кроме того, любая плоскость, проходящая через центр шара, является его плоскостью симметрии. Таких плоскостей в шаре бесчисленное множество. Наконец, шар имеет ещё и центр симметрии. Итак, полная совокупность элементов симметрии шара - .

Геометрия кроме конечных фигур принимает во внимание и бесконечно протяжённые образы. Прямую можно бесконечно продолжить в длину как в одну, так и в другую сторону. Плоскость беспредельно расстилается и в длину, и  в ширину. Пространство безгранично простирается в длину, в ширину и в высоту. Существует ли на земной поверхности и в окружающем нас мире бесконечные тела?

Древесный ствол в первого взгляда напоминает колонну – цилиндрическое тело. На самом же деле он является очень сильно вытянутым острым конусом. При росте вершина уходит всё дальше вверх, а конус ствола становится всё больше похожим на цилиндрическую колонну. Если бы рост дерева продолжался безгранично, то его вершина ушла бы в бесконечность, а ствол принял бы форму беспредельно вытянутого идеального цилиндра.                                                                                       Именно с таких позиций мы и будем определять  бесконечные фигуры в природе. А раз мы условились рассматривать некоторые реальные тела как бесконечно протяжённые, нам придётся ознакомиться с бесконечной симметрией. Оказывается, все элементы симметрии конечных фигур встречаются и на бесконечных: они также могут обладать простыми и сложными осями,  плоскостями и центрами симметрии.  Но бесконечной симметрии присущи ещё три типа специфических, присущих только ей элементов симметрии.

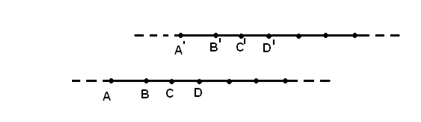·              Трансляция – бесконечная симметрия, сводящаяся к сдвигу или переносу фигуры  параллельно самой себе.

·              Плоскость скользящего отражения Р_t – совокупность плоскости симметрии и параллельного её поступания,  действующих не по отдельности, а совместно. (Рис 18)
Рассмотрим характерный узор с плоскостью скользящего отражения вдоль вертикальной линии. Этот узор часто встречается в природе. Ветви на деревьях, листья на стеблях, прожилки на листьях нередко повторяются в виде этого узора. Встречается он и на некоторых кристаллических образованьях, называемых «скелетными кристаллами» (такие «скелеты» льда образуют зимой на стеклах всем известные ледяные цветы).

·              Винтовая ось L_t – представляет собой совокупность оси симметрии и параллельного ей перемещения (трансляции), действующих не по отдельности, а совместно. Точки фигуры при действии такой симметрии вращаясь и перемещаясь вдоль оси двигаются по винтовым линиям (Рис 20).
Винтовые оси бывают правыми и левыми, в зависимости от того, в какую сторону закручена винтовая линия. По винтовым линиям располагаются ветви на древесных стволах и листья на стеблях.

Попытаемся проделать мысленное путешествие к самым истокам жизни на Земле.  По мере приближения к этим истокам будет всё труднее отличать растения от животных. Ведь отличительным признаком животных является их способность к передвижению. Однако. Морские губки, полипы, усоногие раки и другие беспозвоночные проводят всю жизнь, прикрепившись к морскому дну и не передвигаясь с места на место. Вместе с тем, блуждающие споры водорослей представляют примеры передвигающихся растений. Значит, видимая симметрия и внешняя форма отдельных растений и животных могут быть очень похожими.
Так, простейшие животные, плавающие во взвешенном состоянии в однородной среде без всякого активного поступательного движения, обладают симметрией шара. К ним относятся: радиолярии (рис.68- 69). Билатеральный тип симметрии у простейших встречается относительно редко. Такая симметрия возникает в связи с  активным поступательным движением, например, с ползанием по дну. При этом двусторонняя симметричность вызывается одинаковым воздействием среды на обе половины движущегося животного. Наблюдающееся иногда билатеральное развитие у некоторых представителей иглокожих (морские звёзды, морские ежи) связано или с действием
сильного течения, или с боковым прикреплением животного, или с односторонним притоком пищи.
           В морской среде радиально-лучевая симметрия не препятствует направленному плаванию животного. Такой симметрией обладают, например, медузы, выталкивающие из-под себя воду нижними краями тела, похожего по форме на колокол или, вернее, на абажур лампы. Однако на дне только один вид симметрии вполне согласуется с поступательным передвижением животного, не только не препятствуя, но и всемерно способствуя ему, - это билатеральная симметрия с одной-единственной плоскостью P

Итак, симметрия P играет главенствующую роль в геометрии ползающих по дну беспозвоночных, которым свойственна направленность движений. На каждом из животных, обладающих способностью к такому передвижению, мы неизменно обнаруживаем именно этот вид симметрии, более или менее ясно выраженный.  Сложнейшие формы головоногих (цефалопод), к которым принадлежат осьминоги и каракатицы с их щупальцами и присосками, явно обнаруживают свою подчинённость плоскостной симметрии. Самые примитивные членистоногие (трилобиты) также служат отличной моделью билатерального животного. О насекомых не приходится и говорить. Все они как бы вырезаны из согнутого пополам листка бумаги и имеют две одинаковые половинки – левую и правую.

  На некоторых формах беспозвоночных можно наблюдать бесконечную симметрию.  Присматриваясь к строению кишечно-полостных и в особенности червей, мы обнаруживаем кроме обычной плоскостной симметрии закономерную повторяемость одинаковых частей  вдоль длинного тела животного. Такое тело как бы совмещается само с собой при передвижении по прямой линии, совпадающей с вытянутостью фигуры . Данный случай симметрии зоологи называют «метамерией», а мы уже знаем, что это – трансляция.

У простейших наблюдается ещё один тип симметрии, связанный с тем, что их поступательное движение при плавании нередко сопровождается вращением животного вокруг своей оси – винтовая.

Симметрия  подобия реализуется также в виде винтовых осей с постоянно уменьшающимися деталями, следующими вдоль оси. Например, спиральнозавитые башенкообразные и конусовидные раковины моллюсков, принадлежащих не только к водным, но и наземным формам. К наземным относятся, например, современные улитки, которых можно охарактеризовать с помощью винтовой оси симметрии подобия. Никаких плоскостей симметрии здесь не обнаруживается. Вместе с тем, у самой улитки голова и нога (та часть тела, на которой она ползёт) имеет ясно выраженную билатеральную форму с присущей ей плоскостью симметрии.

При построении зеркально равных фигур мы привыкли опускать из каждой точки исходной фигуры перпендикуляр на зеркальную плоскость симметрии, а затем продолжать его на такое же расстояние. Почему бы не представить себе такую плоскость, в которой отражение осуществляется с помощью косых лучей. Тогда круг отобразится в эллипс (круг и эллипс – гомологичные фигуры). В результате такого образования возникают гомологичные фигуры или части фигур с соответственными точками, но без сохранения равенства между ними. Вспомним матрешек. Откроешь матрешку – а в ней сидит другая, такая же, но только уменьшенная. Во второй находится третья и так далее. Фигуры этих матрешек подобны. Это сходство проявляется и в кочане капусты, и в артишоке, и в цветах розы и водяной лилии. Так появилось понятие операции симметрии подобия. Эти операции представляют собой своеобразные технологии трансляции, отражение в плоскостях, поворотов вокруг осей с той только разницей, что они связаны с одновременным увеличением или уменьшением подобных частей фигуры и расстояний между ними. Симметрия подобия повсеместно проявляется в природе на всем, что растет. Именно к растущим формам относятся бесчисленные фигуры растений, животных, кристаллов. Ветви древесных стволов располагаются вокруг ствола по винтовой линии. Но это не простая винтовая линия: она постепенно суживается к вершине. Да и сами ветви уменьшаются по мере их приближения к вершине дерева. Это и есть пример винтовой оси симметрии подобия. Другими примерами могут служить еловые шишки и початки кукурузы. Винтовые оси симметрии подобия наблюдаются и на спирально закрученных формах раковин. Только здесь они сильно сплющены
       Природные формы с их симметрии с самых первобытных времен и до нынешних дней служили и служат образцами устойчивости, приспособленности, целесообразности. Приглядываясь к телам рыб и водоплавающих птиц, наши далекие предки долбили свои древние челны. Фигура коня послужила моделью для первой примитивной телеги. Дерево подсказало форму шатра. Природные формы, с их законами и симметрией неизменно принимались в внимание изобретателями, конструкторами, строителями. Не даром паровоз так часто сравнивался художниками слова с «огнедышащим драконом», «железным конем». На нем мы снова обнаруживаем свойственную животным билатеральную симметрию, единственная плоскость которой совпадает с направлением движения. А самолеты? Глядя на созданные человеком гигантские птицы, мы снова находим в них всю ту же «симметрию листка», общую и для птиц, и для стрекоз, и для самолетов. Недавно родившаяся на стыке биологии и техники, новая наука «бионика», беря природные объекты в качестве модели для построения тончайших приборов, широко использует  и симметрию их форм. На ту же симметрию природных форм опирается и еще одна молодая дисциплина – «промышленная или техническая эстетика», разрабатывающая наиболее целесообразные, а вместе с тем и наиболее красивые формы для машин, инструментов, мебели.

Форма спиральнозавитой раковины привлекла пристальное внимание Архимеда. В результате им было выведено уравнение спирали. В настоящее время, спираль Архимеда широко применяется в механике. Мало того, она сыграла известную роль в развитии телевидения. В литературных произведениях это описывается так: «В 200 гг. до н.э. великий Архимед вывел закон спирали, носящий его имя; в 1884 году немецкий инженер Пауль Нипков предложил использовать спираль Архимеда для развертки телевизионного изображения. А в 1929 г. советские инженеры П.В. Шмаков, Н.Н. Васильев и Н.Н. Орлов приступили к конструированию первой советской телевизионной системы, основным узлом которой стал спиральный диск Нипкова. Вот куда нас привела скромная ракушка с ее винтовой осью симметрии подобия.
            Как видим, виды симметрий, наблюдаемые нами в природе, находят широкое применение, прежде всего,  в технике. Но и живописцы использовали свойства геометрии для более правильного изображения рисунков. Архитекторы и зодчие в своих творениях также опирались на знания, полученные в области геометрии. Это и симметрии, и пропорции, и подобие, и перспектива.