Задания для подготовки к промежуточной аттестации по алгебре в 11 классе
№ 1. а) Вычислите значение функции: 𝑓(𝑥) = log3 (𝑡𝑔
𝜋
𝑥) при 𝑥 = 3.
б) Вычислите значение функции: 𝑓
при 𝑥 = 𝜋.
в) Вычислите значение функции: 𝑓
при 𝑥 = 8.
г) Вычислите значение функции: 𝑓
при 𝑥 = 𝜋.
№ 2. а) Найдите наименьшее значение функции 𝑦 = 𝑥3 − 2𝑥2 + 𝑥 + 3 на отрезке [1; 4].
б) Найдите точку максимума функции 𝑦 = 𝑥3 − 3𝑥2 + 2.
в) Найдите точку минимума функции 𝑦 = 𝑥3 + 9𝑥2 + 15.
г) Найдите наибольшее значение функции 𝑦 = 𝑥3 + 2𝑥2 + 𝑥 + 3 на отрезке [−4; −1].
№ 3. а) На рисунке изображён график производной функции 𝑓(𝑥), определённой на интервале(−7; 8). Найдите количество точек, в которых касательная к графику функции 𝑓(𝑥) параллельна прямой 𝑦 = 3,5𝑥 + 2 или совпадает с ней.
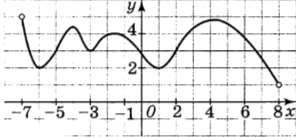
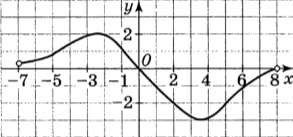
б) На рисунке изображён график производной функции 𝑓(𝑥), определённой на
интервале(−7; 8). Найдите количество точек, в которых касательная к графику функции 𝑓(𝑥) параллельна прямой 𝑦 = −𝑥 + 3 или совпадает с ней.
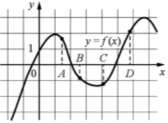
в) На рисунке изображён график функции 𝑦 = 𝑓(𝑥) и
отмечены точки А, В, С и D на оси О𝑥. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ |
|
А |
1) Значение функции в точке отрицательно, и значение производной функции в точке отрицательно |
|
B |
2) Значение функции в точке положительно, и значение производной функции в точке положительно |
|
C |
3) Значение функции в точке отрицательно, а значение производной функции в точке положительно |
|
D |
4) Значение функции в точке положительно, а значение производной функции в точке отрицательно |
|
|
|
г) На рисунке
изображён график функции 𝑦
= 𝑓(𝑥)
и отмечены точки А, В, С и D на оси О𝑥. Пользуясь графиком, поставьте в соответствие каждой точке характеристики функции и её производной.
|
ТОЧКИ |
ХАРАКТЕРИСТИКИ |
|
А |
1) Значение функции в точке положительно, и значение производной функции в точке положительно |
|
B |
2) Значение функции в точке отрицательно, и значение производной функции в точке отрицательно |
|
C |
3) Значение функции в точке положительно, а значение производной функции в точке отрицательно |
|
D |
4) Значение функции в точке отрицательно, а значение производной функции в точке положительно |
№ 4. а) Каждому из четырёх неравенств в левом столбце соответствует одно из решений в правом столбце. Установите соответствие между неравенствами и их решениями.
|
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
А) |
log23(𝑥 − 3) < 1 |
1) 3 < 𝑥 < 6 или 𝑥 > 6 |
|
Б) |
5−𝑥+2 > 0,2 |
2) 3 < 𝑥 < 6 |
|
В) |
𝑥 − 3
(𝑥 − 6)2 |
3) 𝑥 < 3 |
|
Г) |
3𝑥2−9𝑥+18 > 1 |
4) 𝑥 < 3 и 𝑥 > 6 |
б) Каждому из четырёх неравенств в левом столбце соответствует одно из решений в
правом столбце. Установите соответствие между неравенствами и их решениями.
|
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
А) |
log2 𝑥 > 0 |
1) (−∞; 0) ∪ (1; +∞) |
|
Б) |
2−𝑥 > 2 |
2) (1; +∞) |
|
В) |
𝑥
𝑥 − 1 |
3) (−∞; −1) |
|
Г) |
1
𝑥(𝑥 − 1) |
4) (0; 1) |
в) Каждому из четырёх неравенств в левом столбце соответствует одно из решений в
правом столбце. Установите соответствие между неравенствами и их решениями.
|
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
А) |
(𝑥 − 2)2
𝑥 − 1 |
1) (1; +∞) |
|
Б) |
1 2−𝑥
< 2 |
2) (1; 2) |
|
В) |
log2 𝑥 > 1 |
3) (2; +∞) |
|
Г) |
𝑥2 − 3𝑥 + 2 < 0 |
4) (−∞; 1) |
г) Каждому из четырёх неравенств в левом столбце соответствует одно из решений в
правом столбце. Установите соответствие между неравенствами и их решениями.
|
|
НЕРАВЕНСТВА |
РЕШЕНИЯ |
|
А) |
𝑥 − 5
(𝑥 − 3)2 |
1) 𝑥 < 3 или 𝑥 > 5 |
|
Б) |
5−𝑥+1
< |
2) 𝑥 > 3 |
|
В) |
5𝑥2−8𝑥+16 > 1 |
3) 3 < 𝑥 < 5 |
|
Г) |
log2(𝑥 − 3) < 1 |
4) 𝑥 < 3 или 3 < 𝑥 < 5 |
№ 5. а) Решите уравнение: 2𝑙𝑜𝑔42(4𝑠𝑖𝑛𝑥) − 5 log4(4sin 𝑥) + 2 = 0.
б) Решите уравнение: log6(2𝑠𝑖𝑛2𝑥 − 3 sin 𝑥 1) = 0.
в) Решите уравнение: 
.
г) Решите уравнение: 
𝑥.
д) Решите уравнение: 𝑐𝑜𝑠
.
е) Решите уравнение: 
.
ж) Решите уравнение: 4sin2 𝑥 + 8 sin (3𝜋 + 𝑥) + 1 = 0.
2
Задания для подготовки к промежуточной аттестации по алгебре в 11 классе № 1
А 1) Значение функции в точке отрицательно, и значение производной функции в точке отрицательно
НЕРАВЕНСТВА РЕШЕНИЯ
Решите уравнение: . ж) Решите уравнение: 4sin 2 𝑥 + 8 sin ( 3𝜋 + 𝑥) + 1 = 0
© ООО «Знанио»
С вами с 2009 года.
