
Лекция 5.
Детерминированные конечные автоматы
Основные соотношения. Рассмотрим особенности дискретно-детерминированного подхода на примере использования в качестве математического аппарата теории автоматов. Система представляется в виде автомата как некоторого устройства с входными и выходными сигналами, перерабатывающего дискретную информацию и меняющего свои внутренние состояния лишь в допустимые моменты времени. Конечным автоматом называется автомат, у которого множества внутренних состояний, входных и выходных сигналов являются конечными множествами.
Абстрактно конечный автомат (англ. finite automata) можно представить как математическую схему (F-схему), характеризующуюся шестью элементами: конечным множеством Х входных сигналов (входным алфавитом); конечным множеством Y выходных сигналов (выходным алфавитом); конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний); начальным состоянием z0, z0 Î Z; функцией переходов j(z, x); функцией выходов y(z, x). Автомат, задаваемый F-схемой: F = áZ, X, Y, y, j, z0ñ, функционирует в дискретном времени, моментами которого являются такты, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие t-му такту при t = 0, 1, 2, …, через z(t), x(t), y(t). При этом по условию z(0) = z0, а z(t)ÎZ, x(t)ÎX, y(t)ÎY.
Пример. Простейший автомат поведения льва.
Входной алфавит: "антилопа", "охотник".
Внутренние состояния: "сытый", "голодный".
Выходной алфавит: "съесть", "спать", "убежать"
Таблица переходов:
|
|
Сытый |
Голодный |
|
Антилопа |
спать, перейти в состояние «голодный» |
съесть, перейти в состояние «сытый» |
|
Охотник |
убежать, перейти в состояние «голодный» |
убежать |
Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент t = 0, 1, 2, … дискретного времени F-автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t = 0 он всегда находится в начальном состоянии z(0) = z0. В момент t, будучи в состоянии z(t), автомат способен воспринять на входном канале сигнал x(t)ÎX и выдать на выходном канале сигнал y(t) = y[z(t), x(t)], переходя в состояние z(t+1) = j[z(t), x(t)], z(t)Î Z, y(t)ÎY. Абстрактный конечный автомат реализует некоторое отображение множества слов входного алфавита X на множество слов выходного алфавита Y. Другими словами, если на вход конечного автомата, установленного в начальное состояние z0, подавать в некоторой последовательности буквы входного алфавита x(0), x(1), x(2), …, т.е. входное слово, то на выходе автомата будут последовательно появляться буквы выходного алфавита y(0), y(1), y(2), …, образуя выходное слово.
Таким образом, работа конечного автомата происходит по следующей схеме: в каждом t-м такте на вход автомата, находящегося в состоянии z(t), подается некоторый сигнал x(t), на который он реагирует переходом (t+1)-го такта в новое состояние z(t+1) и выдачей некоторого выходного сигнала. Сказанное выше можно описать следующими уравнениями: для F-автомата первого рода, называемого также автоматом Мили,
z(t+1) = j[z(t), x(t)], t = 0, 1, 2, …; (2.15)
y(t) = y[z(t), x(t)], t = 0, 1, 2, …; (2.16)
для F-автомата второго рода
z(t+1) = j[z(t), x(t)], t = 0, 1, 2, …; (2.17)
y(t) = y[z(t), x(t – 1)], t = 1, 2, 3,…. (2.18)
Автомат второго рода, для которого
y(t) = y[z(t)], t = 0, 1, 2, …, (2.19)
т.е. функция выхода не зависит от входной переменной x(t), называется автоматом Мура.
Таким образом, уравнения (2.15)-(2.19), полностью задающие
F-автомат, являются частным случаем уравнений
(2.3) и (2.4), когда
система S – детерминированная и на её
единственный вход поступает дискретный сигнал X.
По числу состояний различают конечные автоматы с памятью и без памяти. Автоматы с памятью имеют более одного состояния, а автоматы без памяти (комбинационные или логические схемы) обладают лишь одним состоянием. При этом, согласно (2.16), работа комбинационной схемы заключается в том, что она ставит в соответствие каждому входному сигналу x(t) определенный выходной сигнал y(t), т.е. реализует логическую функцию вида
y(t) = y[ x(t)], t = 0, 1, 2, … .
Эта функция называется булевой, если алфавит X и Y, которым принадлежат значения сигналов x и y, состоят из двух букв.
По характеру отсчета дискретного времени конечные автоматы делятся на синхронные и асинхронные. В синхронных F-автоматах моменты времени, в которые автомат «считывает» входные сигналы, определяются принудительно синхронизирующими сигналами. После очередного синхронизирующего сигнала с учетом «считанного» и в соответствии с уравнениями (2.15)-(2.19) происходит переход в новое состояние и выдача сигнала на выходе, после чего автомат может воспринимать следующее значение входного сигнала. Таким образом, реакция автомата на каждое значение входного сигнала заканчивается за один такт, длительность которого определяется интервалом между соседними синхронизирующими сигналами. Асинхронный F-автомат считывает входной сигнал непрерывно и поэтому, реагируя на достаточно длинный входной сигнал постоянной величины x, он может, как следует из (2.15)-(2.19), несколько раз изменять состояние, выдавая соответствующее число выходных сигналов, пока не перейдет в устойчивое, которое уже не может быть изменено данным входным сигналом.
Возможные приложения F-схемы. Чтобы задать конечный F-автомат, необходимо описать все элементы множества F = <Z, X, Y, y, j, z0>, т.е. входной, внутренний и выходной алфавиты, а также функции переходов и выходов, причем среди множества состояний необходимо выделить состояние z0, в котором автомат находится в состоянии t = 0. Существуют несколько способов задания работы F-автоматов, но наиболее часто используются табличный, графический и матричный.
В табличном способе задаются таблицы переходов и выходов, строки которых соответствуют входным сигналам автомата, а столбцы – его состояниям. Первый слева столбец соответствует начальному состоянию z0. На пересечении i-й строки и k-го столбца таблицы переходов помещается соответствующее значение j(zk, xi) функции переходов, а в таблице выходов – соответствующее значение y(zk, xi) функции выходов. Для F-автомата Мура обе таблицы можно совместить.
Описание работы F-автомата Мили таблицами переходов j и выходов y иллюстрируется табл. 2.1, а описание F-автомата Мура – таблицей переходов (табл. 2.2).
Таблица 2.1
|
Xi |
zk |
|||
|
z0 |
z1 |
… |
zk |
|
|
Переходы |
||||
|
x1 |
j(z0, x1) |
j(z1, x1) |
… |
j(zk, x1) |
|
x2 |
j(z0, x2) |
j(z1, x2) |
… |
j(zk, x2) |
|
… |
… |
… |
… |
… |
|
xi |
j(z0, xi) |
j(z1, xi) |
… |
j(zk, xi) |
|
Выходы |
||||
|
x1 |
y(z0, x1) |
y(z1, x1) |
… |
y(zk, x1) |
|
x2 |
y(z0, x2) |
y(z1, x2 ) |
… |
y(zk, x2) |
|
… |
… |
… |
… |
… |
|
xi |
y(z0, xi) |
y(z1, xi) |
… |
y(zk, xi) |
Таблица 2.2
|
xi |
y(zk) |
|||
|
y(z0) |
y(z1) |
… |
y(zk) |
|
|
z0 |
z1 |
… |
zk |
|
|
x1 |
j(z0, x1) |
j(z1, x1) |
… |
j(zk, x1) |
|
x2 |
j(z0, x2) |
j(z1, x2) |
… |
j(zk, x2) |
|
… |
… |
… |
… |
… |
|
xi |
j(z0, xi) |
j(z1, xi) |
… |
j(zk, xi) |
Примеры табличного способа задания F-автомата Мили F1 приведены в табл. 2.3, а для F-автомата Мура F2 – в табл. 2.4.
Таблица 2.3
|
xi |
zk |
||
|
z0 |
z1 |
z2 |
|
|
Переходы |
|||
|
x1 |
z2 |
z0 |
z0 |
|
x2 |
z0 |
z2 |
z1 |
|
Выходы |
|||
|
x1 |
y1 |
y1 |
y2 |
|
x2 |
y1 |
y2 |
y1 |
Таблица 2.4
|
|
Y |
||||
|
xi |
y1 |
y1 |
y3 |
y2 |
y3 |
|
|
z0 |
z1 |
z2 |
z3 |
z4 |
|
x1 |
z1 |
z4 |
z4 |
z2 |
z2 |
|
x2 |
z3 |
z1 |
z1 |
z0 |
z0 |
При графическом способе задания конечного автомата используется понятие
направленного графа. Граф автомата представляет собой набор вершин,
соответствующих различным состояниям автомата и соединяющих вершины дуг графа,
соответствующих тем или иным переходам автомата. Если входной сигнал xk вызывает
переход из состояния zi в состояние zj, то на графе автомата дуга, соединяющая
вершину zi c вершиной zj,
обозначается xk. Для того чтобы задать
функцию выходов, дуги графа необходимо отметить соответствующими выходными
сигналами. Для автоматов Мили эта разметка производится так: если входной
сигнал xk действует
на состояние zi, то получается дуга,
исходящая из zi и помеченная xk; эту дугу дополнительно отмечают выходным
сигналом y = y(zi,
xk). Для автомата Мура аналогичная
разметка графа такова: если входной сигнал xk,
действуя на некоторое состояние автомата, вызывает переход в состояние zj, то дугу, направленную в zi и помеченную xk,
дополнительно отмечают выходным
сигналом y = y(zj,
xk).
На рис. 2.4. а, б приведены заданные ранее таблицами F-автоматы Мили F1 и Мура F2 соответственно.
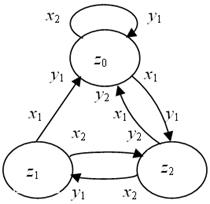
а
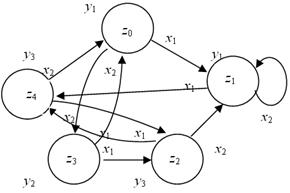
б
Рис. 2.4. Графы автоматов а – Мили и б – Мура
При матричном задании конечного автомата матрица
соединений автомата квадратная С=||сij||,
строки соответствуют исходным состояниям, а столбцы – состояния перехода.
Элемент сij = xk/ys,
стоящий на пересечении
i-й строки и j-го
столбца, в случае автомата Мили соответствует входному сигналу xk, вызывающему переход из состояния zi в состояние zj,
и выходному сигналу ys, выдаваемому
при этом переходе. Для автомата Мили F1,
рассмотренного выше, матрица соединений имеет вид:
 x2 / y1 – x1 / y1
x2 / y1 – x1 / y1
C1= x1 / y1 – x2 / y2 .
x1 / y2 x2 /y1 –
Для F-автомата Мура элемент сij равен множеству входных сигналов на переходе (zi,zj), а выход описывается вектором выходов
 y(z0)
y(z0)
y(z1)
……
![]() = y(zk)
,
= y(zk)
,
……
y(zK)
i-я компонента которого – выходной сигнал, отмечающий состояние zi.
Для рассмотренного выше F-автомата Мура F2 матрицы соединений и вектор выходов имеют вид:
 – x1 – x2 – у1
– x1 – x2 – у1
– x2 – – x1 у1
C2= – x2 – –
x1 ; ![]() = у3
= у3
x2 – x1 – – у2
x2 – x1 – – у3
Для детерминированных автоматов выполняется условие однозначности переходов: автомат, находящийся в некотором состоянии, под действием любого входного сигнала не может перейти более чем в одно состояние. Применительно к графическому способу задания F-автомата это означает, что в графе автомата из любой вершины не могут выходить два и более ребра, отмеченные одним и тем же входным сигналом. А в матрице соединений автомата С в каждой строке любой входной сигнал не должен встречаться более одного раза.
Таким образом, понятие в дискретно-детерминированном подходе к исследованию на моделях свойств объектов является математической абстракцией, удобной для описания широкого класса процессов функционирования реальных объектов в автоматизированных системах управления. С помощью F-автомата можно описать объекты, для которых характерно наличие дискретных состояний, и дискретный характер работы во времени – это элементы и узлы ЭВМ, устройства контроля, регулирования и управления, системы временной и пространственной коммутации в технике обмена информацией и т.д.
Пример моделирования с помощью конечных автоматов
Пример построения конечного автомата (процессора)
для распознавания и обработки записи вещественных чисел
На входе автомата: строка символов, представляющая вещественное число без знака.
На выходе автомата: пара целых чисел: мантисса и порядок или сообщение об ошибке, если число записано неправильно.
Пример.
1. 38.71 Е - 42 → (3871, -44);
2. .9 Е 21 → (9, 20);
3. 4.5.6 .9 → Ошибка;
4. 3. Е 4 → (3, 4);
5. 12 → (12, 0);
6. 1.2 → (12, -1).
На данном примере покажем образец для решения задачи о построении конечного распознающего автомата и обрабатывающего процессора. Разобьем этот процесс на несколько этапов.
1. Выписать один или несколько примеров характерных цепочек, на основе которых:
а) определить входной алфавит;
б) подписать под символами цепочек состояния, моделируя работу автомата;
в) выписать словесные описания состояний.
а) Входной алфавит A={ц Е . + -}; (где ц – цифра 0..9)
б) Примеры.
Входная цепочка: 3 8 . 7 1 Е – 4 2
Состояния автомата: Ø 1 1 2 3 3 4 5 6 6
Или.
Входная цепочка: . 9 Е 2 1.
Состояния автомата: Ø7 3 4 6 6.
в) Ø начальное состояние; ожидание цифры мантиссы, либо точки.
1 – прочитана цифра первой части мантиссы; ожидание еще одной цифры или точки, или символа Е.
2 – прочитана точка; ожидание цифры дробной части или символа Е.
3 – прочитана цифра дробной части мантиссы; ожидание еще одной цифры или символа Е.
4 – прочитан символ Е; ожидание знаков операций +, -, или цифры порядка.
5 – прочитан знак порядка; ожидание цифры порядка.
6 – прочитана цифра порядка; ожидание еще одной цифры.
7 – прочитана точка в качестве 1-го символа входной цепочки; ожидание обязательной цифры дробной части мантиссы.
Еr - состояние ошибки.
2. Построить схему и таблицу переходов конечного автомата.
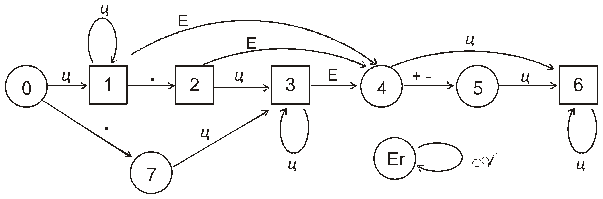
Все неотмеченные стрелками переходы ведут в состояние ошибки Er.
|
|
ц |
Е |
. |
+- |
Допустимость |
|
0 |
1 |
|
7 |
|
0 |
|
1 |
1 |
4 |
2 |
|
1 |
|
2 |
3 |
4 |
|
|
1 |
|
3 |
3 |
4 |
|
|
1 |
|
4 |
6 |
|
|
5 |
0 |
|
5 |
6 |
|
|
|
0 |
|
6 |
6 |
|
|
|
1 |
|
7 |
3 |
|
|
|
0 |
|
Еr |
|
|
|
|
0 |
Здесь все пустые клетки соответствуют переходу в состояние ошибки Er.
3. Привести полученный автомат к минимальному виду.
Существуют специальные математические методы, позволяющие оптимизировать конечные автоматы, то есть находить избыточные состояния автомата. Существуют алгоритмы по приведению автомата к минимальному виду. Из результатов применения подобного алгоритма следует эквивалентность состояний 2 ~ 3.
В достижимости всех состояний нетрудно убедиться глядя на диаграмму переходов автомата. Таким образом для получения минимального приведенного автомата следует провести факторизацию, объединив состояния 2 и 3.
Для удобства дальнейшего описания переименуем состояния следующим образом:
0 → 1
1 → 2
2, 3 → 3
4 → 4
5 → 5
6 → 6
7 → 7
Еr → Еr
Ниже приведена новая диаграмма и таблица переходов конечного автомата.
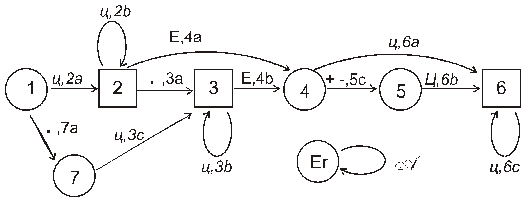
|
Новая таблица переходов: |
|||||
|
|
ц |
Е |
. |
+- |
Доп |
|
1 |
2 |
|
7 |
|
0 |
|
2 |
2 |
4 |
3 |
|
1 |
|
3 |
3 |
4 |
|
|
1 |
|
4 |
6 |
|
|
5 |
0 |
|
5 |
6 |
|
|
|
0 |
|
6 |
6 |
|
|
|
1 |
|
7 |
3 |
|
|
|
0 |
|
Еr |
|
|
|
|
0 |
|
Таблица вызова процедур процессора: |
|||||
|
|
ц |
Е |
. |
+- |
Доп |
|
1 |
2a |
|
7a |
|
|
|
2 |
2b |
4a |
3a |
|
Да1 |
|
3 |
3b |
4b |
|
|
Да2 |
|
4 |
6a |
|
|
5a |
|
|
5 |
6b |
|
|
|
|
|
6 |
6c |
|
|
|
Да3 |
|
7 |
3c |
|
|
|
|
|
Еr |
|
|
|
|
|
4. Построить процессор, обрабатывающий символ конца строки.
(В таблице все пустые клетки соответствуют вызову процедуры «НЕТ», отвергающей входную цепочку). Процедура Да заканчивает работу автомата, допуская входную цепочку и выдавая результат её обработки.
5. Дополнить переходы процессора именами процедур.
Для удобства в данном случае имя процедуры образовано из номера состояния, в которое переходит автомат, дополненное порядковой буквой латинского алфавита (см. также схему на рисунке).
Замечание: если процессор должен выдавать сообщение об ошибках, то следует ввести обозначения для процедур обработки каждого из видов ошибок, заполнив ими все пустые клетки таблицы.
6. Ввести необходимые регистры – переменные, необходимые автомату для получения результата.
Число – регистр значащей части числа (целое число).
Порядок – регистр порядка (целое число).
Счетчик – регистр счетчика цифр, стоящих после (целое число).
Знак - (±1) – знак порядка.
7. Описать процедуры, вызываемые в соответствии с таблицей и обрабатывающие значения регистров процессора.
2а: Число := ц
2в: Число := 10 * Число + ц
3а: Счетчик := 0
3в: Счетчик := Счетчик + 1
Число := 10 * Число + ц
3с: Число := ц; Счетчик =: 1
4а: Счетчик =: 0
4в: Ø
5а: Знак := {+1, если а=’+’ или -1, если a=’-‘} (здесь а – входной символ.)
6а: Знак := +1
Порядок := ц
6в: Порядок := ц
6с: Порядок := 10 * Порядок + ц
7а: Ø
Да1: Порядок := 0
Да2: Порядок := -Счетчик
Да3: Порядок := Знак * Порядок - Счетчик
Здесь символом Æ обозначено отсутствие всякого действия – пустая процедура. В тех случаях, когда целочисленному регистру присваивается символ (например: Счетчик=ц), подразумеваем неявное преобразование символа цифры в число им обозначаемое.
7.Проверить работу автомата (процедуры) на одной или нескольких цепочках так, чтобы каждый переход автомата осуществлялся хотя бы один раз.
В качестве примеров рассмотрим работу автомата по обработке следующих трёх входных цепочек. В скобках указано ожидаемое значение регистров Число и Порядок на выходе процессора.
а) 67.89E-12┤ (6789, -14)
б) 2E3┤ (2,3)
в) .89┤ (3,-1)
|
Входной символ |
Переход в сост., процедура |
Значения регистров |
|||
|
Число |
Порядок |
Счетчик |
Знак |
||
|
- |
1 (начальное) |
- |
- |
- |
- |
|
6 |
2a |
6 |
- |
- |
- |
|
7 |
2b |
67 |
- |
- |
- |
|
. |
3a |
67 |
- |
0 |
- |
|
8 |
3b |
678 |
- |
1 |
- |
|
9 |
3b |
6789 |
- |
2 |
- |
|
E |
4b |
6789 |
- |
2 |
- |
|
- |
5a |
6789 |
- |
2 |
-1 |
|
1 |
6b |
6789 |
1 |
2 |
-1 |
|
2 |
6c |
6789 |
12 |
2 |
-1 |
|
┤ |
Да3 |
6789 |
-14 |
2 |
-1 |
|
- |
1 (начальное) |
- |
- |
- |
- |
|
2 |
2a |
2 |
- |
- |
- |
|
E |
4a |
2 |
- |
0 |
- |
|
3 |
6a |
2 |
3 |
0 |
+1 |
|
┤ |
Да3 |
2 |
3 |
0 |
+1 |
|
- |
1 (начальное) |
- |
- |
- |
- |
|
. |
7a |
- |
- |
- |
- |
|
8 |
3c |
8 |
- |
1 |
- |
|
9 |
3b |
89 |
- |
2 |
- |
|
┤ |
Да2 |
89 |
-2 |
2 |
- |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.