
МБОУ «Гребенская СОШ»
Методическая разработка
«Дифференцированное обучение на уроках математики»
Подготовила методическую разработку
учитель математики:
Решедова Джамиля Мусаевна
Введение
В концепции развития математического образования в Российской Федерации указывается, что математическое образование должно обеспечивать каждого обучающегося развивающей интеллектуальной деятельностью на доступном уровне, используя присущую математике красоту и увлекательность; …»
Актуальным остается вопрос дифференциации обучения математики, позволяющей, с одной стороны, обеспечить базовую математическую подготовку, а с другой – удовлетворить потребности каждого, кто проявляет интерес и способности к предмету.
Положительного результата в учебно-воспитательном процессе можно добиться, учитывая индивидуальные способности и возможности каждого ученика. А так как уровень знаний, познавательных способностей не у всех детей одинаков, то на уроке при коллективной форме работы необходим дифференцированный подход в обучении.
Принцип дифференциации обучения – положение, согласно которому педагогический процесс становится дифференцированным. Одним из основных видов является индивидуальное обучение.
Технология дифференцированного обучения представляет собой совокупность организационных решений, средств и методов дифференцированного обучения, охватывающая определенную часть учебного процесса.
В своей деятельности я стараюсь учитывать признаки технологии дифференцированного обучения:
1. Процессуальный двусторонний характер взаимосвязанной деятельности учителя и обучающегося.
2. Наличие совокупности методов и приемов.
3. Проектирование и организация.
4. Наличие комфортных условий.
Технология дифференцированного обучения – процессуальная система совместной деятельности учителя и обучающегося по проектированию, организации, ориентированию образовательного процесса с целью достижения конкретного результата при обеспечении комфортных условий обучающихся.
Объекты изучения
Для того, чтобы использование технологии дифференцированного обучения принесло положительные результаты, необходимо провести диагностику учебной деятельности обучающихся. Что же должно стать объектом изучения?
1. Отношение обучающегося и класса к учебе.
Изучая мотивацию (цели, потребности, интересы, эмоции, мотивы), которая в значительной степени определяет отношение обучающегося к учебной деятельности, необходимо иметь разные ее источники. Для одних обучающихся источником является само знание, для других – процесс учения, для третьих – взаимоотношения с одноклассниками, учителями, для четвертых – влияние семьи.
Неслучайно психологи выделяют две большие группы мотивов:
1. познавательные мотивы, связанные с содержанием учебной деятельности и процессом ее выполнения;
2. социальные мотивы, в основе которых взаимодействие, общение, сотрудничество обучающегося с другими людьми.
Положительное, постоянное активное отношение к учебной деятельности наблюдается у тех обучающихся, для которых характерно сочетание разных мотивов.
Мотивация учебной деятельности обусловлена также индивидуальными особенностями личности обучающегося, его установками, склонностями, жизненными планами.
2. Направленность познавательного процесса.
Устойчивый познавательный процесс – важный мотив учения. Знать приоритетную направленность интересов, обучающихся крайне важно, чтобы целенаправленно развивать их, облегчить выбор того или другого профиля обучения.
3. Знания и умения.
Диагностика учебной деятельности направлена прежде всего на выявление качественности гарантированных знаний, их глубины, обобщенности, систематичности, мобильности.
Вторая не мене важная сторона – установление уровней знаний: обучающийся умеет лишь воспроизводить знания; или знания применяются в стандартных вариативных ситуациях, или обучающийся оперирует знаниями в условиях переноса, в нестандартных ситуациях.
4. Особенности процесса самостоятельной работы, учебной деятельности обучающихся.
Чтобы эффективно управлять действиями обучающихся, необходимо знать их типичные и индивидуальные затруднения при выполнении заданий, потребность в руководстве учителя. сотрудничестве.
5. Активность, организованность, ответственность, самостоятельность обучающихся.
6. Эффективность применяемых средств и стимулов учебной деятельности.
Обработка данных, в основном, показывает, что в большинстве своем обучающиеся:
Изучив учебные возможности обучающихся своего класса, учитель неоднократно убеждается в том, что достигнуть хороших результатов можно только используя технологию дифференцированного обучения.
Наряду с известными негативными сторонами технологии отмечается много положительных сторон: исключается неоправданная нецелесообразная уравниловка детей; а у учителя появляется возможность более эффективно работать со слабоуспевающими обучающимися, уделять внимание успешным. Реализуется желание успешных обучающихся быстрее и глубже продвигаться в образовании; повышается уровень концепции: сильные утверждаются в своих способностях, слабые получают возможность испытывать учебный успех, избавиться от комплекса неполноценности; повышается уровень мотивации.
Организация самостоятельной работы
На уроках дифференцированного обучения нет равнодушных: сильные работают с максимальной нагрузкой, а средние и слабые тянутся за ними, не теряя веры в свои силы и возможности. А это, по моему убеждению, является главным в обучении. Именно дифференцированная работа позволяет добиться высоких результатов в обучении и помогает научить ребенка самостоятельно работать.
Организация самостоятельной работы – это действия педагогов и обучающихся, направленные на создание педагогических условий, необходимых для своевременного и успешного выполнения задания. Установлено, что форма организации труда влияет на его результат. Форма организации – это определенная расстановка участников учебного процесса, способы взаимодействия учителя и обучающихся, самих школьников между собой.
Классно-урочная система позволяет организовать познавательную деятельность одновременно со всеми обучающимися. Это может быть и фронтальная беседа, и самостоятельная работа, выполняемая в классе под руководством и наблюдением учителя.
Особенности фронтальной формы организации самостоятельной деятельности обучающихся состоит в следующем:
1. все обучающиеся выполняют общее задание для всех;
2. учитель дает инструктаж к выполнению заданий;
3. используются общие приемы организации и руководства действиями подопечных.
Главное преимущество фронтальных работ заключается в том, что здесь возможны коллективные устремления к общей цели, решение единичных задач, побуждающих к сотрудничеству. Промежуточные и конечные результаты самостоятельной работы успешно обсуждаются всеми обучающимися, подвергаются взаимному контролю. Это оказывает существенное влияние на качество знаний и умений, стимулирует познавательный интерес и активность.
Несмотря на то, что обучающиеся получают общее задание, общий инструктаж, каждый работает самостоятельно, индивидуально, стремится достичь цели прежде всего собственными усилиями. Если же это не удается, то при анализе итогов работы в классе каждый имеет возможность послушать правильные ответы своих одноклассников. Таким образом достигается сочетание коллективной и индивидуальной работы, в которую вовлекаются все.
Фронтальная форма организации самостоятельной деятельности наиболее целесообразно тогда, когда важно создать определенный настрой, вызвать интерес к новой теме. Также полезна и важна она на начальном этапе формирования умений, когда обучающиеся овладевают способами выполнения заданий по образцу. Поэтому первыми я использую типовые задачи, общие для всего класса, чтобы, получая общий инструктаж, обучающиеся быстрее освоили механизм применения знаний, усвоили основную схему действий. На этом этапе важную роль играет коллективный анализ типичных ошибок, допускаемых в процессе выполнения заданий.
Фронтальная самостоятельная работа эффективна, если результаты ее обсуждаются в процессе общеклассной беседы, т.е. происходит включение в коллективную деятельность. Каждый получает возможность проверить свой ответ, высказать свое мнение, уточнить, обогатить его суждениями других ребят.
Под индивидуальной самостоятельной работой следует понимать такую, которая предусматривает выполнение индивидуализированных заданий и исключает сотрудничество с обучающимися. Однако она открывает огромные возможности для сотрудничества обучающегося с учителем. Обязанности учителя при этом не менее сложны и ответственны, чем подопечного. Необходим тщательный анализ содержания учебного материала, на основе которого учитель умеет выделить те же вопросы, которые доступны отдельным обучающимся для самостоятельной проработки и важны для развития познавательного интереса.
Технология опыта:
Индивидуальные самостоятельные работы имеют большое значение. Во-первых, возрастает роль самого обучающегося в определении содержания работы, в выборе способов ее выполнения. Во-вторых, возникает возможность сотрудничества учителя и ребенка, особенно при выполнении заданий творческого характера.
Самостоятельные индивидуальные задания использую не только при повторении, но и при объяснении нового материала. Здесь очень важно правильно подобрать дифференцированные задания для каждого. Дифференцированные задания – это система упражнений, выполнение которых поможет глубже и осознаннее усвоить правило и выработать вычислительный навык на его основе. Упражнения должны отличаться простотой, краткостью и точностью. начинать работу надо с более простых упражнений, постепенно продвигаясь к более сложным, требующим необходимых обобщений.
Дифференцированные задания готовлю к уроку заранее, записывая на слайде, карточках. Их делю на два вида:
обязательные задания
Они способствуют умению правильно применять изученное правило; их должно быть огромное количество; они должны быть посильны для каждого обучающегося.
дополнительные задания
Они рассчитаны для тех детей, которые справились с обязательными заданиями и у них есть время для самостоятельной работы. Эти задания повышенной трудности на применение изученного материала, требующие сравнения, анализа, определенных выводов.
Качество и количество упражнений может быть разным, но доступным для усвоения правила на данном этапе урока.
Для успешного усвоения нового материала важны подготовленные упражнения. Это и диктанты, и игры, и самостоятельная работа. Важно при их выполнения и проверке повторить то правило, которое будет необходимо при объяснении новой темы.
Примеры самостоятельных работ
Тема «Сумма внутренних углов выпуклого многоугольника», 8 класс.
1. Объяснительный текст: постройте произвольный выпуклый пятиугольник.
Пусть нам нужно найти сумму всех его внутренних углов. Такая же задача возникает и по отношению к шестиугольнику, семиугольнику и вообще выпуклому n-угольнику.
Для решения поставленной задачи выберите одну из вершин построенного пятиугольника и проведите все выходящие из нее диагонали. Пятиугольник разбивается этими диагоналями на три треугольника (5 – 2 = 3). Сумма всех внутренних углов этих треугольников будет равна сумме всех внутренних углов пятиугольника, поэтому получаем 180° • 3 = 540°.
Заполните таблицу:
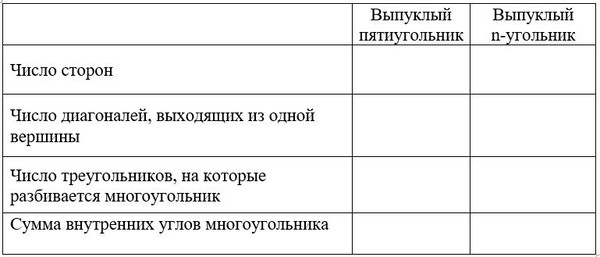
2. Упражнения для самоконтроля
а) Какую теорему мы доказали?
б) Какую мы вывели формулу для вычисления суммы всех внутренних углов выпуклого
многоугольника?
в) Вычислите сумму углов выпуклого восьмиугольника.
3. Основные упражнения
Указание. Произвольную внутреннюю точку многоугольника соедините с его вершинами.
При подготовке к этой самостоятельной работе мы повторили вопросы: какая фигура называется многоугольником, чему равна сумма углов треугольника, четырехугольника, на основании какой теоремы доказательства теорема о сумме углов выпуклого четырехугольника.
Для закрепления какой-либо темы можно проводить решение круговых упражнений. Например:
Решить уравнения:
1. 120 – 5х = 40;
2. 7 • 8 – у = 48;
3. а – 84 : 2 = 8;
4. 2х – х – 32 = 16;
5. 18 • 5 – 2х = 10;
6. 10 • (15 – х) = 50.
Решая первое уравнение, находим корень уравнение 16, это число находится в правой части уравнения № 4, значит, обучающийся должен решать его, затем переходить к уравнению № 2, от него - № 3, № 6, № 5, № 1.
Контрольные и самостоятельные работы по геометрии в восьмых классах даю в трех уровнях сложности, что позволяет осуществить дифференцированный контроль.
Первый уровень соответствует обязательным программным требованиям; второй – среднему уровню сложности; задания третьего уровня предназначены для обучающихся, проявляющих повышенный интерес к математике.
Например, контрольная работа по теме «Четырехугольники» в восьмом классе:
I уровень Вариант 1.
1) Диагонали прямоугольника ABCD пересекаются в точке О, ∠ ABO = 36°. Найдите угол AOD.
2) Найдите углы прямоугольной трапеции, если один из ее углов равен 20°.
3) Стороны параллелограмма относятся как 1 : 2, а его периметр равен 30 см. Найдите стороны параллелограмма.
4) В равнобокой трапеции сумма углов при большем основании равна 96°. Найдите углы трапеции.
5) * Высота BM, проведенная из вершины угла ромба ABCD образует со стороной AB угол 30°, AM = 4 см. Найдите длину диагонали BD ромба, если точка M лежит на стороне AD.
II уровень Вариант 1.
1) Периметр параллелограмма 50 см. Одна из сторон на 5 см больше другой. Найдите длины сторон параллелограмма.
2) Найдите угол между диагоналями прямоугольника, если каждый из них делит угол прямоугольника в отношении 4 : 5.
3) Найдите углы параллелограмма, если одна из его диагоналей является высотой и равна одной из его сторон.
4) В трапеции ABCD диагональ BD перпендикулярна боковой стороне AB, ∠ADB = ∠BDC = 30°. Найдите длину AD, если периметр трапеции 60 см.
5)* В параллелограмме ABCD биссектрисы углов ABC и BCD пересекаются в точке M1. На прямых AB и CD взяты точки K и P так, что А – В – К, D – C – P. Биссектрисы углов KBC и BPC пересекаются в точке M2, M1M2 = 8 см. Найдите AD.
III уровень Вариант 1.
1) В
равнобокой трапеции длина боковой стороны 2d, длины оснований 5d и 7d. Найдите
углы трапеции.
2) В параллелограмме ABCD известно, что Ð А = 60°, АВ =
10, AD = 16. Найдите расстояния от вершин В и D до биссектрисы Ð BCD.
3) В ромбе ABCD биссектриса угла DCA перпендикулярна стороне AD. Найдите углы
ромба.
4) Внутри квадрата ABCD выбрана точка М так, что треугольник AMD
разносторонний. Найдите угол АМВ.
5)* Биссектриса угла С параллелограмма ABCD пересекает сторону AD в точке М и
продолжение стороны АВ за точку А в точке N. Найдите периметр параллелограмма,
если AN = 4, DM = 3.
Урок одной задачи.
Урок одной задачи – это поиск разных способов решения этой задачи.
На уроке одной задачи у обучающегося появляется возможность найти свой способ решения, то есть способ, который ему понятен, в котором он может максимально выразиться.
На уроке одной задачи обучающийся услышит разные рассуждения, мнения, увидит различные приемы решения. Кроме того, у учителя уменьшается возможность навязать свой способ рассуждения, значит, уменьшается потребность учить по шаблону «делай как я», а у обучающегося, наоборот, появляется возможность действовать так, как он этого хочет.
Таким образом, учитель формирует личность, способную думать, отстаивать свое мнение, находить выход из создавшейся ситуации, а в перспективе – разбираться в жизни, в людях. Урок одной задачи не оставляет равнодушными ни одного обучающегося. Возрастает мотивация обучения математике, улучшаются результаты самостоятельных и контрольных работ.
Решение задачи разными способами помогает восполнить пробелы в ранее изученных темах, побуждает обучающихся к поиску различных приемов решения задачи. Для одних уроки одной задачи – это соломинка для спасения в трудном мире математики, которая все же помогает найти свой, понятный путь решения задачи, для других – открывается мир красоты и изящества любимого предмета, для третьих – путь к пониманию в общении с одноклассниками и учителем. Урок одной задачи помогает каждому найти свою нишу для самовыражения и понимания себя и других.
Алгебра, 8 класс. Урок одного уравнения 3x2 + 2x – 1 = 0 (десять способов).
Способ I. По общей формуле: .
Способ II. По формуле с четным коэффициентом b
Способ III. 3x2 + 2x – 1 = 0 (делим обе части уравнения на 3):
по теореме, обратной теореме Виета:
Способ IV. Из условия: если a + c = b, то
Способ V. Выделение полного квадрата:
Способ VI. Метод переброски старшего коэффициента:
Пусть 3x = y, тогда получаем: y2 + 2y – 3 = 0, но a + b + c = 0, значит, т.е. y2 = -3 (или по теореме, обратной теореме Виета). Вернемся к подстановке:
Способ VII. Приведение к виду
Способ VIII. Разложение на множители способом группировки:
Способ IX. Уменьшение степени уравнения: 3x2 + 2x – 1 = 0; подбором находим, что -1 – корень данного уравнения; разделим трехчлен 3x2 + 2x – 1 на x – x1, то есть на x + 1. В результате получим выражение 3x – 1. Данный трехчлен раскладывается на множители: 3x2 + 2x – 1 = (x + 1)(3x - 1). Уравнение принимает вид: (x + 1)(3x - 1).= 0, откуда
Способ X. С помощью графиков.
Заключение
Построение дифференцированного процесса обучения невозможно без учета индивидуальности каждого обучающегося как личности и присущим только ему личностным особенностям;
Обучение, основанное на уровневой дифференциации, не является целью, это средство развития личностных особенностей как индивидуальности.
Только раскрывая индивидуальные особенности каждого обучающегося в развитии, т.е. в дифференцированном процессе обучения, можно обеспечить осуществление личностно-ориентированного процесса обучения.
Основная задача дифференцированной организации учебной деятельности — раскрыть индивидуальность, помочь ей развиться, устояться, проявиться, обрести избирательность и устойчивость к социальным воздействиям.
Дифференцированное обучение – это:
Технология дифференцированного обучения представляет собой совокупность организационных решений, средств и методов дифференцированного обучения, охватывающих определенную часть учебного процесса.
Положительные аспекты
Отрицательные аспекты
Литература:
1. Арсланьян В. « Групповая форма работы». // Математика.-2006. - №16.
2. Бродский, Я., Павлов А. Повторим математику. Тесты разного уровня/Я. Бродский, А. Павлов. – Математика № 33, 1999.
3. Груденов, Я.И. Совершенствование методики работы учителя математики/ Я.И. Груденов. – М: Просвещение, 1990.
4. Денищева, Л.О., Кузнецова Л.В., Лурье И.А. и др. Зачеты в системе дифференцированного обучения математике/ Л.О Денищева и др.– М: Просвещение, 1993.
5. Жужгова К.А. « Дифференциация в процессе обучения математике», 2005.
6. Кочетов, К., Баранова Т. Система работы с увлеченными математикой школьниками/К. . Кочетов// Журнал Математика № 11, 2001.
7. Лернер, И.Я. Проблемное обучение/ Серия «Педагогика и психология», №7, - М, 1974
8. Лоповок, Л.М. 1000 проблемных задач по математике/ Л.М. Лоповок. – М: Просвещение, 1995
9. Матюшкин, А.М. Проблемные ситуации в мышлении и обучении/ А.М Матюшкин. – М: Педагогика, 1972.- 306 с.
10. Махмутов, М.И. Организация проблемного обучения в школе: Кн. для учителей/ М.И. Махмутов. – М: Просвещение, 1977.
11. Миракова, Т.Н. Развивающие задачи на уроках математики в 5-8 классах/Т.Н. Миракова// Квантор. -1991. -№ 3
12. Оконь В. Основы проблемного обучения. – М.: Просвещение, 1968.
13. Осмоловская,И.М. Как организовать дифференцированное обучение/Библиотека журнала «Директор школы» - 2002. – сентябрь.- 12 с.
14. Петрова, Е. Дифференцированное обучение/Е Петрова//Математика № 16, 17, 18.- 2001.
15. Пойа, Д. Математическое открытие/ Д. Пойа. – М, 1970.
16. Сойер, У.У. Прелюдия к математике/ У.У. Сойер – М: Просвещение, 1972.- 303 с.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.