Методическая разработка для учащихся 9 класса "Исполнитель Робот. Задание ОГЭ 15.1"

Методическая разработка по теме
«Исполнитель Робот. Задание ОГЭ 15.1»
для учащихся 9 класса

1.Теоретическая подготовка

Исполнитель Робот умеет перемещаться по лабиринту, начерченному на плоскости, разбитой на клетки. Между соседними (по сторонам) клетками может стоять стена, через которую Робот пройти не может.

У Робота есть девять команд. Четыре команды – это команды-приказы, они управляют перемещениями робота:

вверх, вниз, влево, вправо

При выполнении любой из этих команд Робот перемещается на одну клетку соответственно: вверх, вниз, влево, вправо. Если Робот получит команду передвижения сквозь стену, то он разрушится.

Также у Робота есть команда-приказ закрасить, при которой закрашивается клетка, в которой Робот находится в настоящий момент.

Ещё четыре команды – это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырёх возможных направлений:

сверху свободно, снизу свободно, слева свободно, справа свободно

Также существуют команды проверки наличия стены в каждом из четырёх возможных направлений:

сверху стена, снизу стена, слева стена, справа стена

Эти команды можно использовать вместе с условием «eсли», имеющим следующий вид:

если условие то
последовательность команд
все

Здесь условие – одна из команд проверки условия.

Последовательность команд – это одна или несколько любых команд-приказов.

Например, для передвижения на одну клетку вправо, если справа нет стенки и закрашивания клетки, можно использовать такой алгоритм:

если справа свободно то
вправо
закрасить
все

В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не, например:

если (справа свободно) и (не снизу свободно) то
вправо
все

Для повторения последовательности команд можно использовать цикл «пока», имеющий следующий вид:

нц пока условие
последовательность команд
кц

В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не, например:

если (справа свободно) и (не снизу свободно) то

вправо

все

Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:

нц пока справа свободно
вправо
кц

2. Как запустить среду для Робота

Пуск – Кумир – Кумир – Стандарт (или синий ярлык с буквой К на рабочем столе).

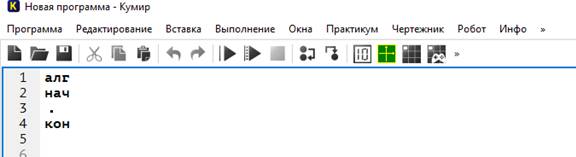
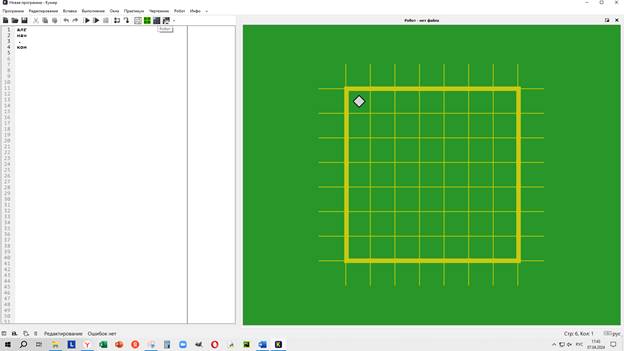
Поле Робота можно приближать и удалять вращением колесика мыши.

Прежде чем писать программу, нужно создать обстановку на поле, соответствующую условию задачи.

Для этого в главном меню выбрать Робот – Редактировать обстановку.

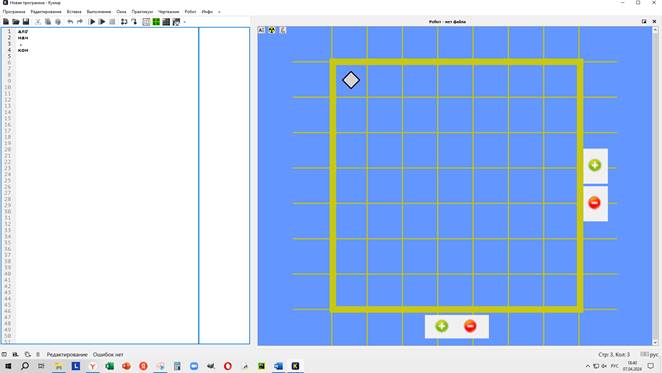
Поле меняет цвет (на голубом поле редактируется обстановка, на зеленом – выполняется программа!)

Количество клеток по горизонтали и по вертикали регулируется значками «плюс» и «минус». Приближение и удаление поля выполняется так же колесиком мыши.

Стенки устанавливаются щелчком мыши по границе клеток. Убираются так же.

Робот обозначен ромбом, он устанавливается в исходное положение перетаскиванием в нужную клетку.

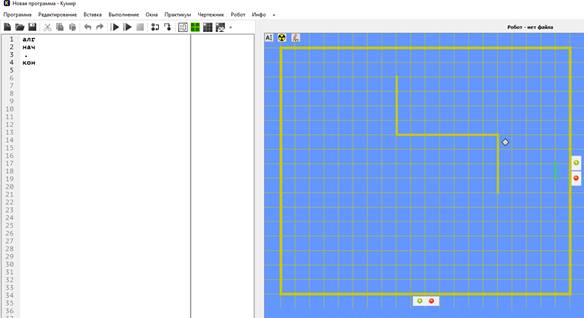
После создания обстановки опять выбрать Робот – снять галочку у «Редактировать обстановку».

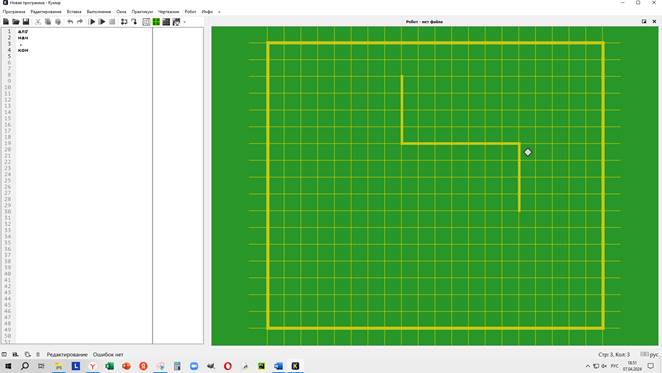
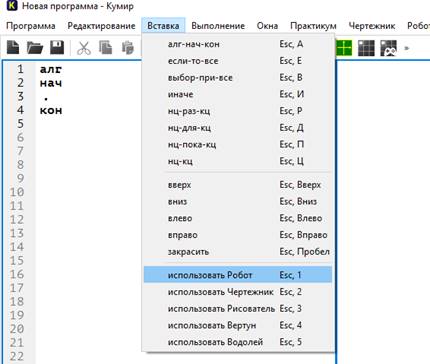
Прежде, чем писать программу, нужно ВКЛЮЧИТЬ ИСПОЛНИТЕЛЯ РОБОТ!!!

Получается вот так:

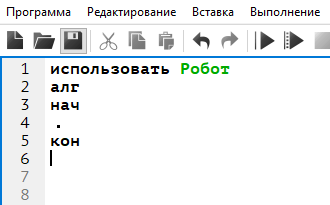
Программа пишется между служебными словами нач и кон.

Обращайте внимание на точки в начале команды – они показывают уровень вложенности команд (какая команда входит в какую конструкцию).

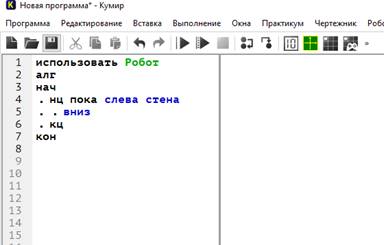
Запуск программы на выполнение – кнопки с изображением треугольника. В поле справа показываются результаты проверки условий и сообщения об ошибках.

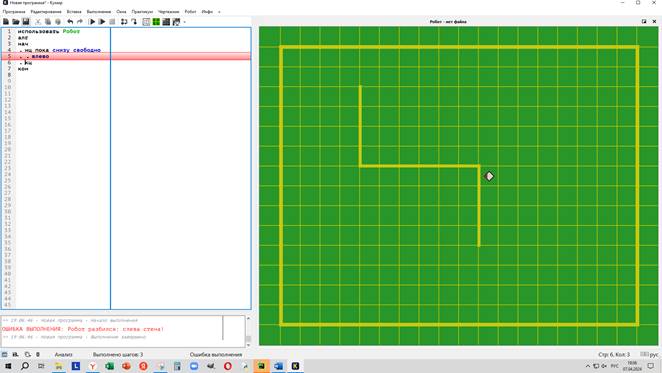
В данной ситуации Робот разбился о стену.

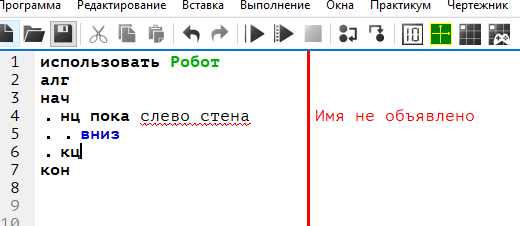
В данной ситуации неверно написана команда.

Если программа выполняется верно, рекомендуется изменить обстановку, например, увеличить или уменьшить длину стены и т.д. в соответствии с условием задачи и запустить еще раз.

В конце работы необходимо сохранить программу (см. далее).

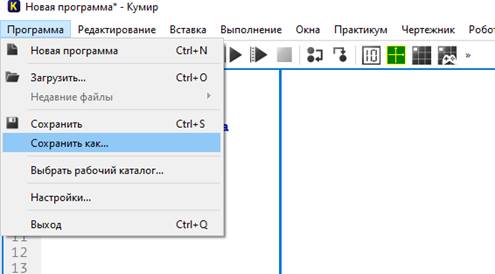
Открывается внутренняя папка Кумира. Сюда сохранять свои программы НЕ НАДО!!!

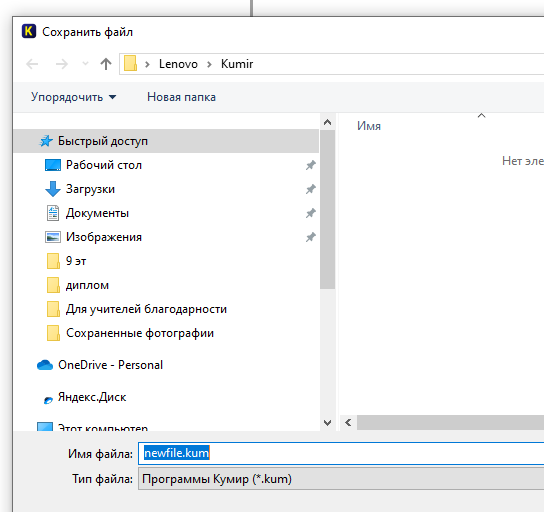
Выберите нужную папку, например, Рабочий стол – Личная папка. Введите имя файла, соответствующее задаче, которую вы решили.

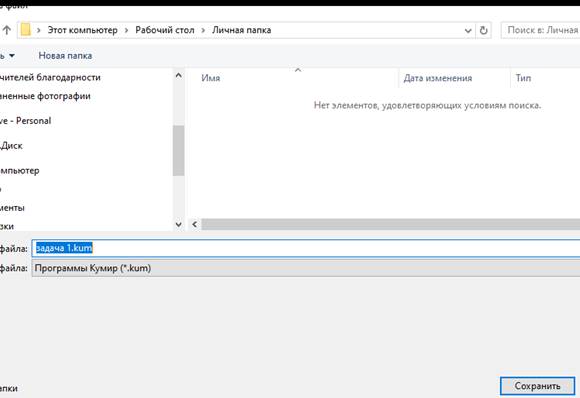
Обратите внимание на расширение файла – kum – это специальное расширение среды Кумир. По сути дела, это обычный текстовый файл, в котором содержится текст вашей программы. Чтобы его запустить его на выполнение, нужно открыть Кумир и перетащить туда файл, , а затем уже запустить программу на выполнение.

Далее находятся задачи, которые необходимо выполнить. Создайте на рабочем слоте Личную папку и сохраняйте каждую программу под соответствующим номеру задачи именем. Обстановки сохранять в Кумире тоже можно, в отдельном специальном файле, но в данных задачах это не требуется.

3. Задачи для Робота

Задача 1.

На бесконечном поле имеется вертикальная стена. Длина стены неизвестна.

От верхнего конца стены влево отходит горизонтальная стена также неизвестной длины. Робот находится в клетке, расположенной справа от нижнего края вертикальной стены.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

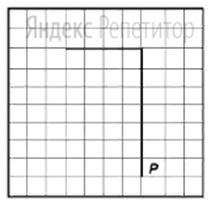
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные правее вертикальной стены, выше горизонтальной стены и угловую клетку.

Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля.

Сохраните алгоритм в формате программы Кумир.

Задача 2.

На бесконечном поле имеются две вертикальные стены и одна горизонтальная, соединяющая нижний конец правой и верхний конец левой вертикальных стен. Длины стен неизвестны. Робот находится в клетке, расположенной слева от верхнего края правой вертикальной стены, рядом со стеной.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

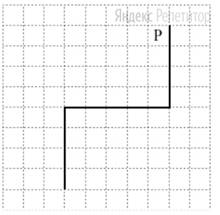
Напишите для Робота алгоритм, закрашивающий все клетки, примыкающие к вертикальным стенам справа. Робот должен закрасить только клетки, удовлетворяющие данному условию.

Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

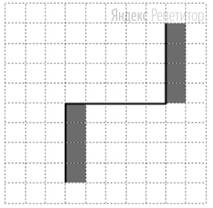
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля.

Сохраните алгоритм в формате программы Кумир.

Задача 3.

На бесконечном поле имеется стена, состоящая из трёх последовательных отрезков: вправо, вниз, влево. Все отрезки неизвестной длины. Робот находится в клетке, расположенной в нижнем углу, который образуется вторым и третьим отрезками.

На рисунке указан один из возможных способов расположения стены и Робота (Робот обозначен буквой «Р»).

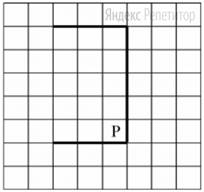
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные справа от второго отрезка. Робот должен закрасить только клетки, удовлетворяющие данному условию.

Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля.

Сохраните алгоритм в формате программы Кумир.

Задача 4.

Робот находится в нижней клетке узкого вертикального коридора. Ширина коридора – одна клетка, длина коридора может быть произвольной. Возможный вариант начального расположения Робота приведён на рисунке (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки внутри коридора и возвращающий Робота в исходную позицию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

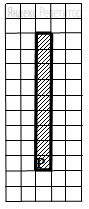
Алгоритм должен решать задачу для произвольного конечного размера коридора. При исполнении алгоритма Робот не должен разрушиться.

Сохраните алгоритм в формате программы Кумир.

Задача 5.

На бесконечном поле есть горизонтальная и вертикальная стены. Правый конец горизонтальной стены соединён с верхним концом вертикальной стены. Длины стен неизвестны. В каждой стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной непосредственно под горизонтальной стеной у её левого конца.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно ниже горизонтальной стены и левее вертикальной стены, кроме клетки, в которой находится Робот перед выполнением программы.

Проходы должны остаться не закрашенными. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведённого выше рисунка Робот должен закрасить следующие клетки.

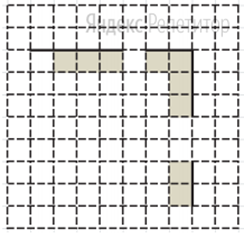
При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным.

Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен.

Сохраните алгоритм в формате программы Кумир.

Задача 6.

На бесконечном поле имеются две одинаковые вертикальные параллельные стены, расположенные на одинаковой высоте и отстоящие друг от друга более чем на одну клетку. Длины стен неизвестны. Робот находится в одной из клеток, расположенных непосредственно справа от правой стены.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

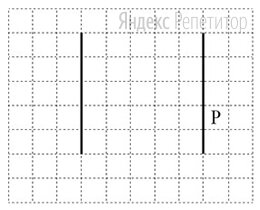
Напишите для Робота алгоритм, закрашивающий все клетки, примыкающие к вертикальным стенам справа. Робот должен закрасить только клетки, удовлетворяющие данному условию.

Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Сохраните алгоритм в формате программы Кумир.

Задача 7.

На бесконечном поле имеются четыре стены, расположенные в форме прямоугольника. Длины вертикальных и горизонтальных стен неизвестны. Робот находится в клетке, расположенной в левом верхнем углу прямоугольника.

На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

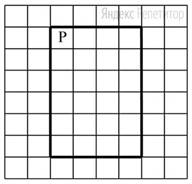
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные с внутренних сторон правой и нижней стен. Робот должен закрасить только клетки, удовлетворяющие данному условию.

Например, для приведённого выше рисунка Робот должен закрасить следующие клетки (см. рисунок).

Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться.

Сохраните алгоритм в формате программы Кумир.

Задача 8.

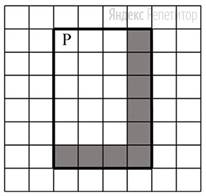
На бесконечном поле есть горизонтальная и вертикальная стены. Правый конец горизонтальной стены соединен с верхним концом вертикальной стены. Длины стен неизвестны. В горизонтальной стене есть ровно один проход, точное место прохода и его ширина неизвестны. Робот находится в клетке, расположенной рядом с вертикальной стеной слева от ее нижнего конца. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

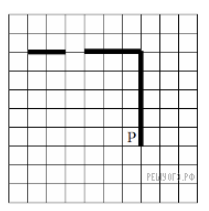
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно выше и ниже горизонтальной стены. Проход должен остаться не закрашенным. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведенного выше рисунка Робот должен закрасить следующие клетки (см. рис.).

При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться. Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для любого допустимого расположения стен и любого расположения и размера проходов внутри стен.

Задача 9.

На бесконечном поле имеется лестница. Сначала лестница спускается вниз справа налево, затем спускается вниз слева направо. Высота каждой ступени  — одна клетка, ширина  — две клетки. Робот находится справа от верхней ступени лестницы. Количество ступенек, ведущих влево, и количество ступенек, ведущих вправо, неизвестно. На рисунке указан один из возможных способов расположения лестницы и Робота (Робот обозначен буквой «Р»).

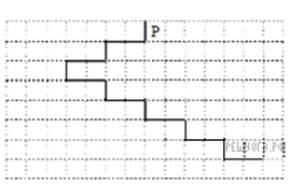
Напишите для Робота алгоритм, закрашивающий все клетки, расположенные непосредственно над ступенями лестницы, спускающейся слева направо. Требуется закрасить только клетки, удовлетворяющие данному условию. Например, для приведенного выше рисунка Робот должен закрасить следующие клетки (см. рис.).

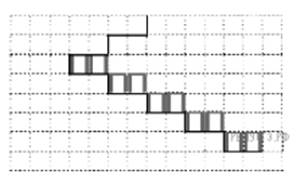
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Задача 10.

На бесконечном поле имеется прямоугольник, ограниченный стенами. Длины сторон прямоугольника неизвестны. Робот находится внутри прямоугольника. На рисунке указан один из возможных способов расположения стен и Робота (Робот обозначен буквой «Р»).

Напишите для Робота алгоритм, закрашивающий верхние угловые клетки. Робот должен закрасить только клетки, удовлетворяющие данному условию. Например, для приведенного выше рисунка Робот должен закрасить следующие клетки (см. рис.).

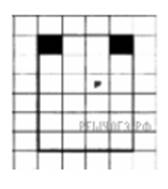
Конечное расположение Робота может быть произвольным. Алгоритм должен решать задачу для произвольного размера поля и любого допустимого расположения стен внутри прямоугольного поля. При исполнении алгоритма Робот не должен разрушиться, выполнение алгоритма должно завершиться.

Список использованных источников

1.     Сдам ГИА: решу ОГЭ. https://inf-oge.sdamgia.ru/test?theme=20

2.     Яндекс. Репетитор. https://yandex.ru/tutor/subject/?subject_id=20

Скачано с www.znanio.ru