Методическая разработка "Использование здоровьесберегающих технологий на уроках математики"

Муниципальное бюджетное общеобразовательное учреждение

 «Средняя общеобразовательная школа № 39» города Чебоксары Чувашской Республики

с углубленным изучением отдельных предметов

 

 

 

 

 

Использование здоровьесберегающих технологий

на уроках математики

 

 

 

 

 

 

 

 

                                                                 Работу выполнила:

 

                                                           учитель математики

                                                                              I квалификационной категории

                                                                                 МБОУ «СОШ № 39» г.Чебоксары

                                                                        Семенова Эльвира Фирсовна

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Чебоксары  2019

Содержание

 

 

Введение ………………………………………………………………….……..  3

Использование здоровьесберегающих технологий на уроках математики ...  4

Урок алгебры в 7 классе……………………………………………..……….... 12

Заключение ………………………………………………………………….…. 16

Приложения .…………………………………………………………………… 18

Список использованной литературы………………………………………...... 27

 

 

Введение

 

Успешность обучения в школе определяется уровнем состояния здоровья, с которым ребенок пришел в школу, что является исходным фоном на старте обучения. На этом фоне в дальнейшем не менее важна и правильная организация учебной деятельности.

Многочисленные исследования последних лет показывают, что около 25-30% детей, приходящих в 1-е классы, имеют те или иные отклонения в состоянии здоровья. За период обучения в школе число здоровых детей уменьшается в 4 раза, число близоруких детей увеличивается с 1 класса к выпускным с 3,9 до 12,3%, с нервно-психическими расстройствами – с 5,6 до 16,4%, нарушениями осанки – с 1,9 до 16,8%. Одна из частых патологий у школьников – нарушение остроты зрения, составляющее в ряде регионов России до 30-40%.

В настоящее время образовательный процесс характеризуется его интенсификацией, и именно с этим фактором  специалисты связывают 40% детско-подростковой патологии, т.к. частое следствие интенсификации учебного процесса – возникновение у учащихся состояний усталости, утомления, переутомления. В свою очередь переутомление создает предпосылки развития острых и хронических нарушений здоровья, развития нервных, психосоматических и других заболеваний.

В связи с этим проблема здоровья детей сегодня как никогда актуальна. В настоящее время можно с уверенностью утверждать, что именно учитель в состоянии сделать для здоровья современного ученика больше, чем врач. Это не значит, что педагог должен выполнять обязанности медицинского работника. Просто учитель должен работать так, чтобы обучение детей в школе не наносило ущерба здоровью школьников.   

Здоровьесберегающие образовательные технологии можно рассматривать как совокупность тех принципов, приемов, методов педагогической работы, которые дополняя традиционные технологии обучения и воспитания, наделяют их признаком здоровьесбережения, т.е. цель здоровьесберегающих  технологий обучения - обеспечить школьнику возможность сохранения здоровья за период обучения в школе.

 

Использование здоровьесберегающих технологий на уроках математики

 

Для достижения целей здоровьесберегающих  технологий обучения применяются следующие группы средств:

1)      Средства двигательной направленности;

2)      Гигиенические факторы;

3)      Психолого-педагогические факторы.

 

К средствам двигательной направленности относятся такие двигательные действия, которые направлены на реализацию задач здоровьесберегающих  образовательных технологий обучения. Это – физкультминутки (приложение 1), эмоциональные разрядки, подвижные игры с дидактической направленностью.

В течение дня концентрация внимания не одинакова – она колеблется. У каждого человека есть свои собственные циклы, длительность которых от 90 до 110 минут. В конце каждого такого цикла мозг нуждается в кратковременном отдыхе.

В среднем дети 5-8 лет могут интенсивно, без перерывов учиться в течение 5-7 минут, не более. Дети 9-13 лет – в течение 8-12 минут, юноши и девушки 14-18 лет –

в течении 12-15 минут. После этого должна обязательно следовать пауза.

Существуют и другие причины необходимости введения в процесс обучения пауз и фаз рефлексии. Эти причины следующие:

1. Многое в процессе обучения происходит неосознанно и спонтанно. Для осмысления и структуирования результатов обучения требуется специальное время.
2. Для того, чтобы найти в обучении свои личностные смыслы, человеку необходимо время, свободное от поступления новой информации и решения задач.
3. После завершения урока учебный процесс еще долго не заканчивается. Не сознавая этого, мы в течение какого-то времени перерабатываем эту информацию. На житейском языке это звучит обычно таким образом: «эта информация должна отлежаться».

Все это означает, что после интенсивной работы необходим перерыв, во время которого активизируются отделы головного мозга, не работающие ранее.

Упражнения  для физкультминуток выполняют важные функции:

1. Они снижают уровень напряжения и дают возможность ученикам расслабиться.
2. Они делают процесс обучения более эффективным, поскольку активизируют все важнейшие системы человеческого организма.
3. Они создают в группе обстановку доверия и доброжелательности.

С позиций здоровьесбережения польза от выполнения нескольких физических

упражнений будет наибольшей, если учитывать следующие условия:

1. Состав упражнений физкультминутки должен зависеть от особенностей урока ( в какой вид деятельности были включены учащиеся до этого, каково их состояние и т.д.)
2. Обязательным является эмоциональная составляющая физкультминутки. Занятие должно проводиться на положительном эмоциональном фоне.
3. Учителю необходимо выработать для каждого класса 2-3 условных вербально-поведенческих знака, позволяющих быстрее и эффективнее переключать школьников в другой режим деятельности.

 

К гигиеническим средствам достижения целей здоровьесберегающих  образовательных технологий обучения, содействующим укреплению здоровья и стимулирующим развитие адаптивных свойств организма, относятся: санитарно-гигиенических требований, регламентированных СанПиНами; личная и общественная гигиена (чистота тела, чистота мест занятия, воздуха и т.д.); проветривание и влажная уборка помещений, ограничение предельного уровня учебной нагрузки во избежание преутомления.  Несоблюдение гигиенических требований к проведению занятий снижает положительный эффект здоровьесберегающих  образовательных технологий обучения.

 

Основные гигиенические критерии рациональной организации урока ( по Н.К.Смирнову )

 

Факторы урока	Гигиенический рациональный уровень урока
Плотность урока	Не менее 60% и не более 75-80%
Число видов учебной деятельности	4 – 7
Средняя продолжительность различных видов деятельности	Не более 10 мин.
Частота чередования различных видов учебной деятельности	Смена не позже чем через 7 – 10 мин.
Число видов преподавания	Не менее 3
Чередование видов преподавания	Не позже чем через 10 – 15 мин.
Наличие эмоциональных разрядок (число)	2 – 3
Место и длительность применения ТСО	В соответствии с гигиеническими нормами
Чередование позы	Поза чередуется в соответствии с видом работы. Учитель наблюдает за посадкой учащихся
Физкультминутки	Две за урок. Состоящие из 3 легких упражнений, по 3 – 5 повторений каждого
Психологический климат	Преобладают положительные эмоции
Момент наступления утомления учащихся (по снижению учебной активности)	Не ранее чем через 40 мин.

 

Психолого-педагогические факторы

Наиболее часто встречающиеся проблемы с «энергетикой», повышенная утомляемость, истощаемость детей, вызывающая колебания, а затем и полное падение внимания. Учитель может противопоставить утомлению – повышение мотивации и дозировку заданий, обеспечение отдыха.

Обеспечение мотивации.

Если ребенок не объект, а один из субъектов обучения, если он эмоционально вовлечен в процесс учения и задания ему по силам, то возникает «аффективно-волевая подоплека» обучения, которая обеспечивает естественное повышение работоспособности, повышение эффективности работы мозга, которое не идет в ущерб здоровью.

Для обеспечения мотивации важно обучение «по единицам, а не по элементам», предпочтение значимого осмысленного материала.

Принцип целостности

Элементарные и в то же время осмысленные действия лучше осваиваются и запоминаются. Исходя из этого, следует по возможности избегать чисто технических заданий и предлагать доступные творческие задания.

Таким образом, выбор теории должен определяться познавательными возможностями и необходимостью обеспечения мотивации.

Эмоциональная вовлеченность ребенка в процесс обучения позволяет значительно упростить проблему обеспечения прочного запоминания. Эмоционально-значимый материал проходит более глубокую обработку и лучше запоминается. При этом необходимо учитывать закономерности угасания следа, в соответствии с которыми сначала необходимо частое подкрепление следа, а затем все более редкое. Система повторения является необходимым условием доступности учебного процесса и сохранения учебной мотивации.

Обеспечение адекватного восстановления сил.

Смена видов деятельности, регулярное чередование периодов напряженной активной работы и расслабления, смена произвольной и эмоциональной активации необходимы во избежание переутомления детей. При этом следует иметь в виду, что даже сидение за партой без возможности активно двигаться может утомлять детей. Особенно это существенно для детей младшего школьного возраста. Нарушение осанки, опорно-двигательного аппарата - частое следствие чрезмерных требований авторитарного учителя, не задумывающегося об организации регулярных передышек и отдыха для своих учеников.

Для сохранения мотивации и работоспособности очень важно осознание успешности обучения. Если учитель умеет показать успешность ученика в обучении, его действия вызывают психотерапевтический эффект. При этом учителю нет необходимости быть необъективным – он может выделить какой-то аспект работы, похвалить за старание в определенный период времени. Если ребенок часто неуспешен, в предлагаемых ему заданиях следует придерживаться правила «одной трудности», чтобы ребенок мог сосредоточиться на чем-то одном. Таким образом, необходим выбор адекватной для детей сложности заданий.

Индивидуальный подход к детям предполагает учет, во-первых личности ребенка и социальных факторов его развития и, во-вторых, состояния его высших психических функций, т.е. анализ индивидуально-типологических особенностей учащихся и выделение сильных и слабых сторон развития высших психических функций. Учитель должен выстраивать учебные задачи от простых к сложным относительно слабого звена и оказывать помощь (подсказку), позволяющие выполнить функции слабого звена.

Принцип активности предполагает  в учащихся высокую степень самостоятельности, инициативности и творчества, а творческий характер образовательного процесса - необходимое условие здоровьесбережения.

Творческое усвоение знаний обеспечивает проблемный урок.

Проблемные ситуации с удивлением

Пример:             Дается запись :       2 + 5 * 3 = 17                      2 + 5 * 3 = 21  

Вопрос:        Почему левые части одинаковы, а правые отличаются?

Реакция удивления школьников означает возникновение проблемной ситуации .

Эмоциональное переживание возникает у школьников при столкновении с противоречием.

Постановка учебной проблемы с мотивирующим приемом.

Ребята хотят искать ответ на вопрос, который поставили сами, стремятся изучать тему, которую они лично сформулировали или которой их заинтриговали.

Ставить проблему совершенно обязательно, т.к. она мотивирует школьников к усвоению нового материала, включая в работу весь класс, активно задействует всю познавательную сферу: внимание, память, мышление, речь. Проблемный диалог требует больше времени, но при этом обеспечивает понимание материала. Поэтому закрепление идет быстрее и легче.

Проблемный диалог сначала накрывает школьника волной интереса к новому материалу, а затем дарит ему острую радость самостоятельного открытия знаний. Для ребят «учение с увлечением», значительно снижает нервные нагрузки. Таким образом, именно проблемный диалог - здоровьесберегающая  технология.

Формулирование темы урока.

На проблемном уроке тема может быть озвучена не только до, но и после открытия знания, причем не только учителем, но и школьниками.

Художественная форма выражения мысли.

Научные знания можно выразить художественно. При этом знания оседают в памяти благодаря яркому образу. Конкретными формами могут являться метафора, загадка, стихотворение.

Например, термин «скобки» можно выразить так:

Метафора:              скобки – регулировщик, показывающий кому ехать первым.

Загадка:                   в примерах бывает, первое действие называет.

Стихотворение:     скобки найдем, остальное потом.

            Художественные задания даются на дом, потому что на уроках времени на их выполнение просто нет. Они не являются обязательными для каждого ученика и предлагаются по желанию, т.к. для одних такое задание может оказаться захватывающе интересным, а для других – запредельным и повергающим в стресс. Поэтому пусть у школьника будет право выбора.

            В процессе игры вырабатывается умение мыслить системно, продуктивно, пробуждается стремление к поиску новых идей, а это уже шаг к творчеству.

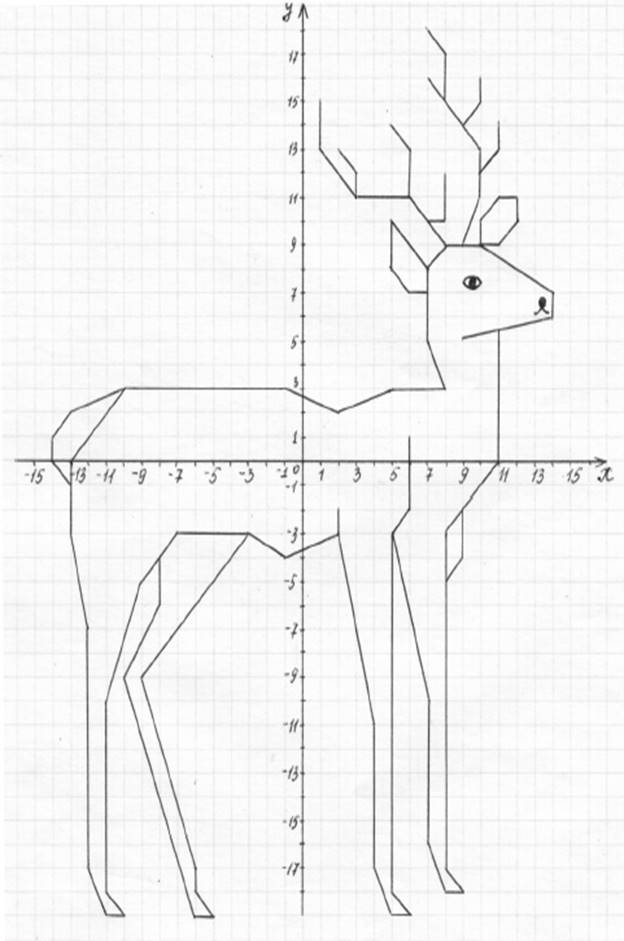
            Рисуем по координатам  (приложение 2)

Даны координаты точек. Нужно каждую из них изобразить на координатной плоскости, последовательно соединить с предыдущей отрезком, в результате получится определенный рисунок. Можно предложить обратное задание: нарисовать самим любой рисунок, имеющий конфигурацию ломанной, и записать координаты вершин.

            Игровые ситуации

Создание игровых ситуаций на уроках математики повышает интерес к математике, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность, чувство соревнования, взаимопомощь.В большинстве случаев они применяются в качестве вспомогательного средства для возбуждения познавательного интереса и создания проблемных ситуаций. Это настраивает учащихся на изучение определенного материала и не требует дополнительного времени для разъяснения правил игры.

            Игровая ситуация создается в процессе выполнения практических заданий.

Задача 1. Построить треугольники по трем сторонам.

1)      АВ = 7, АС = 2, ВС = 3

2)      АВ = 4, АС = 3, ВС = 7

3)      АВ = 3, АС = 2, ВС = 8

Выполняя задание, ребята убеждаются в невозможности такого построения. Как следствие этого, актуализируются знания об условии существования треугольника.

Задача 2. Построить треугольники по трем заданным углам

1) А = 37⁰, В = 28⁰, С = 90⁰

2) А = 72⁰, В = 50⁰, С = 110⁰

3) А = 23⁰, В = 50⁰, С = 38⁰

В данном задании не выполняется условие о сумме внутренних углов треугольника. Создается проблемная ситуация.

Задача 3. Учащимся предлагается найти сумму углов 5-угольника, 6-угольника,

7-угольника и т.д. с помощью транспортира на чертежах. Школьники убеждаются, что измерением практически невозможно найти точно сумму внутренних углов выпуклого n-угольника, Возникает потребность  в теоретическом обосновании этой проблемы, в выводе формулы, которая даст возможность найти  сумму внутренних углов любого        n-угольника,

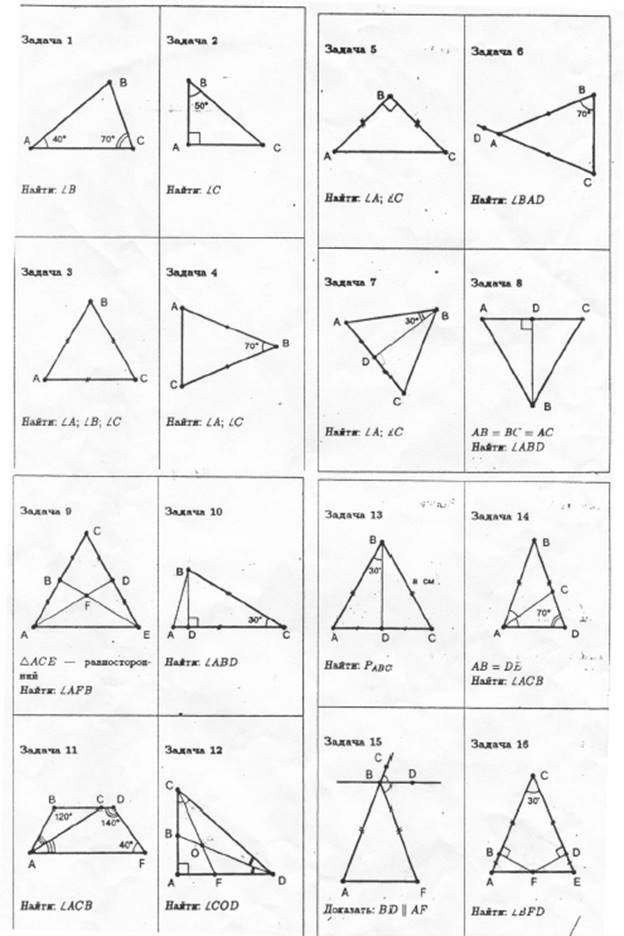
            Игровые ситуации с использованием задач-рисунков (приложение 3)

При работе с задачами-рисунками учитель легко определяет степень усвоения учащимися материала, выявляет пробелы в знаниях. Если для закрепления материала отводится весь урок, то здесь нужно соблюдать последовательность перехода от простого к сложному.

Игровая ситуация при нахождении  замаскированной ошибки

Задача 1.      Дано a > b >0    Из него следует

a ( b - a )  >  b( b - a );

ab – a²  >  b² – ab;

0 > a²  -2ab- b²

0 > ( a – b )²

( a – b )² , где а ≠ b, есть число положительное. Получили, что положительное число меньше нуля.

В этой ситуации учащиеся задумываются. Где в преобразованиях допущена ошибка, 

которая привела к неверному результату?

Задача 2.       Дано    >           Из него следует

()²  > ()³. В силу возрастания функции y = log ₁₀ x,

lg()²  > lg()³, отсюда    2 lg() > 3 lg()

После сокращения на lg(),  получаем 2 > 3

В чем ошибка доказательства?

Игровая ситуация ,содержащая жизненные факты.

При решении задачи возникает необходимость в выводе новой формулы.

Задача. Перед выводом формулы суммы n членов геометрической прогрессии школьникам предлагается такая жизненная ситуация.

            Однажды незнакомец постучал в окно к богатому купцу и предложил такую сделку: «Я буду ежедневно в течение 30 дней приносить тебе по 100 000 р. А ты мне в первый день дашь 1к., во второй день за 100 000 р – 2к. и так каждый день будешь увеличивать предыдущее число денег в два раза. Если тебе выгодна сделка, то с завтрашнего дня начнем».

            Создается проблемная ситуация, кто в этой сделке проиграл: купец или незнакомец? Учащиеся видят, что громоздкая работа по складыванию чисел требует времени и приходят к выводу, что необходима определенная формула.

            Использование занимательных задач.

Задача по рассказу Л.Н.Толстого «Много ли человеку земли надо?» при изучении темы «Решение задач на отыскание наибольшего и наименьшего значений».

В рассказе говорится о том, как крестьянин Пахом, который мечтал о собственной земле и собрал наконец желанную сумму, предстал перед требованием старшины: «Сколько за день земли обойдешь, вся твоя будет за 1000р. Но если к заходу солнца не возвратишься на место, с которого вышел, пропали твои деньги». Выбежал утром Пахом, прибежал на место и упал без чувств, обежав четырехугольник в форме прямоугольной трапеции с периметром 40 км. Наибольшую ли площадь при данном периметре получил Пахом?

Использование буквенных кодов при проверке результатов решения задач и примеров.

Задача. Предлагается 2 задания, к которым приведены 4 варианта ответа в виде буквенного кода. Необходимо выбрать верный вариант. В результате решения всех заданий получается зашифрованное слово.

 

 

 

1. Найти наибольшее значение функции                         1. Найти наименьшее значение функции  

     () =- 4  на  [0; 9]                                                   () =+    на  [1;4]                                                     

     1) ро   -        -4               3) ки   -        1                                  1) те   -       6                3) жа   -       6.25 

     2) ко   -        -3               4) се    -       0                                  2) се    -      -6                 4)  ко    -        10

 

2. Найти катеты прямоугольного треугольника,              2.Число 147 разложили на два положительных

    имеющего наибольшую площадь среди всех               слагаемых так, чтобы произведение одного

    треугольников, у которых сумма длин                             них на квадратный корень другого было

    гипотенузы и одного из катетов равна 21.                        наибольшим.

    Записать наименьший катет.                                              Записать наибольшее слагаемое.

 

     1) ло   -        5               3) ра   -        7                                   1) ма   -        49                3) мя   -         98                                        

1. Найти наименьшее значение функции                            1. Найти наибольшее значение функции

    () = 2³- 9²  на  [-1; 4]                                                 () = - + 2  на  [-2;3] 

     1) во     -           -11            3) мо    -        -27                        1) са   -           2.5            3) но   -              0 

     2) жа   -             0             4) ти    -        -16                        2) лу   -            2              4) ли    -             1

    

2.Число π представили в виде суммы двух поло-           2. Найти положительное число, после вычитания

    жительных слагаемых так, чтобы сумма куба                из которого куба этого числа получается наи-     

    первого слагаемого и утроенного второго сла-               большая разность.

    была  гаемого наименьшей. Найти наименьшее               

    слагаемое.                                                                                                                                  

     1) ра   -         √ π  -1          3) ба   -              π -1                   1) па   -                         3) жа   -                                               

 

Таким образом, системное и комплексное использование всех средств здоровьесберегающих технологий на уроках позволяет решать задачи педагогики оздоровления в условиях инноваций образования.
Урок алгебры в 7 классе

 

Тема :               Разложение многочлена на множители несколькими

способами

 

Цель:                   Обобщить и повторить способы разложения многочлена на множители

 

Задачи:               Проверить и откорректировать знания учащихся по данной теме,   

                               вызвать интерес, активность и самостоятельность учащихся, укрепить

                               дружеские отношения

 

 

План:

1. Организационный момент                                           -   1     мин
2. Проверка местности                                                      -   5     мин
3. Составление карты гонки                                             -   7     мин
4. Гонка по пересеченной местности                              -   10   мин
5. Внезапная остановка – авария                                      -   5    мин
6. Привал                                                                            -   7     мин
7. Финиш                                                                            -    7    мин
8. Итоги урока                                                                    -    2    мин
9. Домашнее задание                                                         -    1    мин

 

 

Ход урока

 

 

Урок - математическое ралли.

Класс-это экипаж машины, которому предстоит совершить пробег по местности со множеством препятствий. Преодолеть эти препятствия экипаж сможет, если он достаточно хорошо знает способы разложения многочлена.

 

1 этап   ралли – Проверка местности.

             Здесь  вспоминаем способы разложения многочлена на множители

 

Пока класс вспоминает способы разложения, по карточкам выполняют задания

 3 человека.

 

Карточка №1

Разложите на множители:

а)   3х² – 75 а²

б)   а² – 8аb + 16b²

в)   х³ + 2х² +  х

Карточка №2

Разложите на множители:

а)   ах² – 4 а

б)   -6а² + 12аb - 6b²

в)   ах² -  2аху + ау²

Карточка №3

Разложите на множители:

а)   5х² – 45

б)   ах² – 4ах + 4а

в)   -2х² -  8х - 8

 

Вопросы для проверки:

 

1. Что значит разложить многочлен на множители?
2. Какие способы разложения многочлена вы знаете?
3. Какие формулы сокращенного умножения вы знаете?
4. Каков алгоритм разложения многочлена на множители?

 

 2 этап   ралли – Составление карты гонки

 

 На каждой парте лежит по 1 экземпляру домино. Учащиеся должны его разложить, чтобы получилась «цепочка» формул. Домино считается разложенным, если все карточки использованы, причем крайние половинки первой и последней карточки должны быть пустыми. Если же использованы не все карточки, значит допущена ошибка.

Если все разложено верно, то перевернув карточки, можно прочитать зашифрованную фразу :« Знания – сила»

 

( с – 9 )2

З
 

с2 - 18с + 81

( 9 + с )2

Н

81 +18с + с2

81 – с2

А

( 9 - с )( 9 + с )

( - с + 9а )2

Н

81 а2 - 18ас + с2

( - с - 9а )2

И

с2 + 18ас + 81а2

( - с2 + 9а )2

Я

81 а2 - 18ас2 + с4

( - с2 + 3а )(  с2 + 3а )

-

9 а2  -  с4

с3 + 729а3

С

( с + 9а )( с2 - 9ас + 81а2)

729с3 -  а3

И

(9с - а )( 81с2 + 9ас + а2)

(-9а + с )( с2 + 9ас + 81а2)

Л

с3 - 729а3

А

 

???   Как Вы понимаете смысл полученной фразы?

 

Для тех, кто быстро разложил домино, на доске вывешены 4 карточки с заданием:

 

Замените знак * одночленом так, чтобы получившийся трехчлен можно было представить в виде квадрата двучлена (последнее задание попробуйте выполнить разными способами

 

16х² +   *   +  у²                                                       25  –  10а    +  *

49р² –  14р +  *                                                        *   –  36аb  +  *

 

Физкультминутка.

1) Упражнения для шеи

2) Упражнения для кистей рук

3) Упражнения для  глаз

3 этап   ралли -  Гонка по пересеченной местности

                              Выполняется задания из учебника  Алимов Ш.А., Алгебра 7 класс

                              № 414(2),  415(2, 4),  417(1, 6)

№ 414  2) Доказать, что при любых значениях х, у верно равенство:

                 ( х – 2у )( х + 2у )( х² + 4у² ) =  х⁴ -16у⁴

№ 415       Разложите на множители на многочлен:

             2)  mn – kn – m² + 2mk – k²

             4)  c² – 2c + 1 – d² -2de – e²

№ 417      Решите уравнения:

            1)  ( 3х – 1 )² – (3х – 2 )² = 0

            2)  (3х + 2)( 3х - 2) – (3х – 4 )² = 28

 

4 этап   ралли. Поскольку в ралли случаются внезапные остановки, у нас тоже небольшая

                            авария – необходимо устранить неисправность нашего автомобиля.

 

На доске приведены решения примеров, но в них допущены ошибки. Учащиеся должны их найти и объяснить, почему они допущены.

 

1) m⁶ - n¹² = (m³ - n⁶)( m³ - n⁶)

2) ( 4а⁵ + b )( 16a¹⁰ – 4a⁵b +  b² ) = 64a¹⁵ -  b³

3) ( 7c + 3d⁴ )² = 7c² + 21cd⁴ + 9d⁸

4) 16 a⁸b³ - 24a⁵b⁷ + 8a²b = 8a²b ( 2a⁴b² - 3a³b⁶ )

5) ( 5x² – 0,02y³)( 5x² + 0,02y³) = 25 x² – 0,004y⁶

6) 64 m⁹ - 8 n¹² = ( 4 m³ – 2 n⁴ )( 16 m⁶ - 8 m³ n⁴ + 4 n⁸ )

7) ( 3p – 2q )³ = 27p³ – 54p²q – 18pq² + 8q³

 

                                                Физкультминутка.

 

Мы сидели и писали,

Мышцы тела все устали.

Потянулись и зевнули,

Спинки дружно все прогнули,

Повернулись вправо, влево –

Стало гибким наше тело.

И на стуле скок, скок, скок,

Ну как будто колобок.

А теперь попляшут ножки:

Пробежали по дорожке

Быстро-быстро – топ, топ, топ.

И в ладоши - хлоп, хлоп, хлоп.

Ножки вытянем вперед,

Влево, вправо поворот.

Чтобы мышцы сильнее стали,

Поработают суставы.

Ножки выше поднимаем

И в коленочках сгибаем,

Подбородком дотянулись

И друг другу улыбнулись.

Головой все повращаем

И урок наш продолжаем.

 

5 этап   ралли.      Сделаем привал: отдохнем на поляне и нарвем цветы. Но цветы

необыкновенные. Каждый лепесток цветка – это задание на составление и разложение многочлена по формулам сокращенного умножения, используя выражения, находящиеся в центре цветка.

                       

 

 

6 этап   ралли  - Финиш

Чтобы успешно пересечь линию финиша, каждому члену экипажа необходимо выполнить самостоятельно из дидактических материалов на стр. 90      № 1 (в) , № 3 (а)

 

№ 1     Разложите на множители:

            в) 18с – 2р²с

 

№ 3     Разложите на множители:

            а) ( с + 5)с² – ( с + 5 )2с + ( с + 5 )

 

Через некоторое время один ученик зачитывает свое решение и ответ. Класс проверяет и ставит себе оценку. За все выполненные задания – «5» , за 1 задание – «4».

 

Подведение итогов урока и выставление оценок за работу в классе.

 

Домашнее задание:        № 414 (1) , 415 (1, 3) , 416

 

 

Заключение

 

В последние годы на фоне экологического и социального неблагополучия и продолжающейся интенсификации школьного образования отмечается нарастающее ухудшение здоровья детей.

В большинстве исследований отмечается четкая зависимость роста отклонений в состоянии здоровья от объема и интенсивности учебной нагрузки. Многие дети приходят в школу недостаточно готовыми к обучению с точки зрения их психофизического развития.  В условиях систематических школьных перегрузок они оказываются неуспевающими учениками или учениками, успехи которых в школе достигаются ценой здоровья. Постоянное пребывание в ситуации неуспешности или тревожного ожидания неуспеха усугубляет поведенческие и нервно-психические отклонения и нередко толкает к асоциальным формам поведения. Чтобы выйти из этого замкнутого круга, и требуются охраняющие здоровье технологии обучения.

Одной из важнейших задач по реализации здоровьесберегающих  технологий является использование активных, творческих методов обучения. Их применение снижает риск появления у школьников переутомления, способствует более гармоническому развитию личности.

Творческий характер образовательного процесса – крайне необходимое условие здоровьесбережения. Включение ребенка в творческий процесс не только природосообразно, способствует развитию личности учащегося, но и снижает вероятность наступления утомления. Обучение без творческого заряда – неинтересно, а значит, в той или иной степени, является насилием над собой и другими, насилие же разрушительно для здоровья, как через формирование усталости, так и само по себе.

Обязательным элементом здоровьесберегающей организации урока в соответствии с современными требованиями являются физкультминутки.

Усилия по внедрению даже самых передовых здоровьесберегающих  технологий останутся безрезультатными, если школьники будут перегружены большим объемом домашних заданий, если с большим напряжением будут заниматься в школе.

Таким образом, педагогические технологии должны способствовать такой организации учебного процесса, чтобы дети успешно развивались как психически, так и физически. От правильной организации урока, уровня его гигиенической рациональности во многом зависит функциональное состояние школьников в процессе учебной

деятельности, возможность длительно поддерживать умственную работоспособность на высоком уровне и предупреждать преждевременное наступление утомления.

 

 

 

Следует помнить, что содержание и формы учебной деятельности оказывают серьезнейшее влияние (положительное или негативное) на состояние и перспективы здоровья детей. Учебно-образовательный процесс осуществляется по здоровье-сберегающим  технологиям, если при реализации используемой педагогической системы решается задача сохранения здоровья учащихся.

 

 

 

 

Приложения

 

Приложение 1.         Гимнастика

 

1.      Движение глазами

Это упражнение придаст глазам больше силы.

• Вы должны двигать только глазами. Держите голову прямо, поднимите глаза максимально вверх, попытайтесь даже смотреть над головой. Потом опустите взгляд как можно ниже, как будто вы хотите рассмотреть свой подбородок. Сделайте так пару раз. Теперь быстро посмотрите вправо, попытайтесь увидеть пространство за своим правым ухом, потом также быстро переведите взгляд влево и попытайтесь заглянуть за левое ухо. Сделайте так пару раз, двигая глазами довольно быстро.
• Теперь вы должны сделать круговые движения глазами. Сделайте так три раза. Дайте глазам отдых – закройте их и пару раз глубоко вдохните. Затем вы должны снова двигать глазами по кругу, но в другую сторону. Снова дайте глазам отдохнуть, закройте их и трижды глубоко вдохните. И под конец представьте себе, что вы видите перед собой лежащую восьмерку.

 

2. Расслабление глаз

Это упражнение ослабляет напряжение, расслабляет глазные нервы, а в некоторой степени успокаивает ум.

• Разогреваем руки, потерев одну ладонь о другую. Делаем это до тех пор, пока руки не станут теплыми. Теперь нужно облокотиться на стол перед собой, сложить пальцы обеих рук в два полушария и мягко прикрыть ими глаза. Почувствуйте, как приятны для глаз тепло и темнота. Можно усилить это чувство, сделав при этом пару глубоких вдохов. Представьте себе, что при вдохе наполняются не только легкие, но и глаза свежим кислородом, что делает их более свежими и сильными.

 

3. Расслабление челюсти

      Это упражнение хорошо действует на мускулатуру челюсти. Расслабляет

      мышцы лица. Таким образом, активизируется большая часть головного мозга, т.к.

     50% моторного и сенсорного отделов коры головного мозга больших полушарий   

     руководят нашей челюстью и ртом.  Это упражнение прекрасно подходит для

     всех учебных процессов, в которых задействован вербальный интеллект.

• Быстро двигаем нижней челюстью, справа налево. Ощутите мускулы, которые помогают в этом. Затем наберите в рот воздуха и раздуйте щеки, дайте воздуху заполнить дальние уголки своего рта. При этом раздуйте сначала левую сторону, потом правую, потом переднюю часть рта.

 

4. Стимуляция ушей

Это упражнение улучшает слух, кроме того, после него начинает отчетливей восприниматься собственный голос. В некоторых случаях подобный массаж ушей даже вызывает из памяти информацию, которую мы перед этим напрасно пытались вспомнить. Это упражнение должно повторяться как можно чаще.

• Возьмите обеими руками внешнюю часть уха, и потяните туда-сюда очень бережно.
• Массируйте край уха и немного выверните его наружу, начните с верха уха, а потом, медленно массируя, перемещайтесь вниз. Теперь сложите средним указательным пальцем обеих рук букву V. Приложите оба пальца к голове, так ухо оказалось в середине. Начните двигать пальцами вверх-вниз, крепко прижимая их к голове. А затем сделайте из пальцев другой руки полушарие и прикройте им ухо. Потом кончиками пальцев другой руки пару раз постучите по этому куполу. Почувствуйте хлопки в костях черепа, таким образом, вы возбуждаете не только нервы уха, но и мозг.
• Повторите то же самое с другим ухом.

 

5. Звезды с небес

Это упражнение расслабляет руки, плечи и позвоночник и, кроме того, улучшает

дыхание.

• Встаньте, поставьте ноги врозь на ширину плеч. Поднимите руки высоко над головой и вытягивайте их все выше вверх. Сначала можно свою правую руку сделать совсем  длиной, как если бы хотелось достать с неба звездочку. Потом позволить правой стороне расслабиться и вытянуть вверх левую руку. При этом представьте себе, что хотите схватить с неба «одной левой». Почувствуйте, как удлиняется верхняя часть тела, плечи, руки, пальцы. Сделайте так еще пару раз, доставайте с неба звездочки попеременно правой и левой рукой. При этом равномерно глубоко дышите.

 

6. Сильные руки

Эти простые упражнения снимают напряжения рук и спины.

• Кисти рук сжали в кулачки, покрутили запястья, разжали. Повторите это упражнение несколько раз.
• Обхватите руками край стула, на котором сидите, обопритесь на него и теперь как можно сильнее потяните на себя стул так, как если бы вам хотелось приподняться от пола вместе со стулом. Затем расслабленно опустите руки вдоль тела. При этом сделайте глубокий вдох и мысленный выдох. Отдохните мгновенье и повторите все еще два раза.

 

7. Источник энергии

Это классическое упражнение. Оно расслабляет затылочную и плечевую мускулатуру и улучшает дыхание. В головной мозг поступает много кислорода, за счет чего улучшается еще и слух и зрение.

• Положите руки на стол перед собой. Выдохните и позвольте своей голове медленно опуститься вниз. Почувствуйте, мускулы вашего затылка растянулись, полностью расслабьте плечи. Теперь снова медленно поднимите голову и при этом сделайте вдох. Дайте голове полностью откинуться назад, пока вам не покажется, что ваша грудная клетка распахнулась и наполнилась воздухом. Когда вы снова будете выдыхать, делайте это медленно и снова опустите голову вниз, пока подбородок вновь не ляжет на грудь. Подарите себе три таких особенных освежающих вдоха.

 

8. Расслабление ног

Это упражнение активизирует кровообращение ног.

• Сядьте поудобнее, облокотитесь на спинку стула, вытяните перед собой ноги, вытяните на себя стопы. Почувствуйте, как растягиваются икроножные мышцы.
• Теперь покрутите стопами сначала в одну сторону, затем в другую.

 

9. Быстрое дыхание

Для здоровых и крепких участников это упражнение безопасно. За такой короткий промежуток времени организм автоматически выравнивает уровень кислорода в крови. Участникам же с повышенным кровяным давлением это упражнение не рекомендуется.

Если вам хочется взбодриться и иметь ясную голову, можете сделать следующее:

• Сядьте поудобнее и начните в течение 10 секунд в быстром темпе вдыхать и выдыхать через нос с закрытым ртом. Обратите внимание на то, как вы себя при этом чувствуете.
• Теперь еще раз подышите таким быстрым способом в течение 15 секунд. Может быть те ощущения, которые возникают, уже знакомы вам по занятиям спортом, танцами или йогой. При этом прибывают свежие силы.
• Эту дыхательную технику вы можете всегда выполнять в те минуты, когда надо быть сосредоточенным и полностью сконцентрированным.

 

10. Психическое расслабление через воображение и мысли образы

• Представьте себе, как вы мысленно купаетесь в солнечных лучах, вдыхаете свежий воздух. Вспомните приятные или смешные случаи и т.д.

 

В случае даже незначительных успехов целесообразно похвалить себя, мысленно говоря: «Молодец!», «Умница!», «Здорово получилось!». Надо находить возможность хвалить себя в течение дня не менее 3-5 раз.

 

 

 

 

 

 

 

 

 

Приложение 2. 

 

 

 

 

 

Приложение 3. 

 

 

 

 

Список использованной литературы

 

 

1. Ахутина Т.В. Здоровьесберегающие технологии: нейропсихологический подход.

      //Вопросы психологии, 2002 №4

2. Вайнбаум Я.С. Дозирование физических нагрузок школьников. М.,Просвещение,1991
3. Гигиенические проблемы охраны здоровья // Материалы научно-практической конференции. Самара, 2000
4. Занимательная математика. 5-11 классы. (как сделать уроки нескучными)

      / автор-составитель Гаврилова Т.Д.,  Волгоград: Учитель, 2004

5. Игры и упражнения для укрепления здоровья детей. //Педсовет, 2006, №4
6. Ильющенков В.В., Берсенева Т.А. Здоровье и образование. СПБ., 1993
7. Калинова Г.С., Мягкова А.Н. Учебная нагрузка и здоровье школьников //Человек. Культура. Здоровье. М.Генезис, 1997
8. Киколов А.И. Обучение и здоровье: Методическое пособие. М.,1988
9. Ковалько В.И. Здоровьесберегающие технологии. М.,: ВАКО, 2004
10. Коваленко В.Г. Дидактические игры на уроках математики. М., 1990
11. Коваленко Т. Творчество на уроках математики. //Народное образование, 1992, № 7
12. Кокорева З.А. Охрана и укрепление здоровья детей в современных образовательных технологиях. //Образование, 2003, №8
13. Кучма В.Р., Сердюковская Г.Н., Демин А.К. Руководство по гигиене и охране здоровья школьников. М., 2000
14. Мельникова Е.Л. Проблемный урок, или как открывать знания с учениками: пособие для учителя. М., 2002
15. Методические рекомендации: Здоровьесберегающие технологии в общеобразовательной школе: методология анализа, формы, методы, опыт применения / Под ред. М.М.Безруких, В.Д.Сонькина. М.,2002
16. Оникул П.Р. 19 игр по математике. Союз, СПБ.,1999
17. Педагогика и психология здоровья / Под ред. Н.К.Смирнова. М.: АПК и ПРО, 2003
18. Раппор И.К. Принципы и механизмы здоровьесберегающих технологий в общеобразовательной школе. //Здоровье населения и среда обитания, 2005, №1
19. Севрук А.И., Юнина Е.А. Здоровьесберегающий урок. //Школьные технологии, 2004, №2
20. Селевко Г.К. Современные образовательные технологии. М., 1998
21. Смирнов Н.К. Здоровьесберегающие образовательные технологии в работе учителя и школы. М., АРКТИ, 2003
22. Современные образовательные технологии. Основные понятия и обзор

       /автор-составитель Г.Н. Петровский. Мн,:НИО, 2000

23. Спиваковская А.С. Игра – это серьезно. М., Педагогика, 1981
24. Фопель К. Энергия паузы. М., 2001
25. Щуркова Н.Е., Питюков В.Ю., Савченко А.П., Осипова Е.А. Новые технологии воспитательного процесса. М., 1993
26. Якиманская И.С. Личностно-ориентированное обучение в современной школе. М.,1996