Методическая разработка Основные величины, характеризующие синусоидальный ток, напряжение и ЭДС

Методическая разработка

по МДК 01.01 Устройство автомобилей

на тему

 «Основные величины, характеризующие синусоидальный ток, напряжение и ЭДС»

2021

Цель занятия:

1.     Изучить тему Основные величины, характеризующие синусоидальный ток, напряжение и ЭДС

Время:  2 часа

Место: кабинет Автомобильные эксплуатационные материалы

Учебно - материальное обеспечение:

Плакаты, презентации, лабораторное оборудование.

Распределение времени занятия:

Вступительная часть                                                                      5 мин;

Проверка подготовки обучающихся к занятию                             5 мин;

Учебные вопросы занятия                                                              25 мин;

Домашнее задание                                                                         5 мин;

Заключение                                                                                    5 мин.

Содержание занятия

Вступительная часть

–        принять рапорт дежурного по группе;

–        проверить наличие студентов и их готовность к занятию;

–        ответить на вопросы, которые возникли при подготовке к занятию на самостоятельной работе;

–        провести опрос по ранее изученному материалу:

–        Опрос рекомендуется провести устно, задавая вопросы и вызывая одного-двух студентов для ответа,

Основные величины, характеризующие синусоидальные ток, напряжение и ЭДС

Этими основными величинами являются:

-     мгновенное значение;

-     амплитудное значение;

-     начальная фаза;

-     действующее значение;

-     среднее значение;

-     комплекс действующего или амплитудного значения и др.

3.1.1 Мгновенное значение. Мгновенное значение величины а показывает закон ее изменения и записывается в виде:

                                                                                            (3.1)

где – амплитуда (максимальное значение) величины;

– угловая частота, рад/с;

t – текущее значение времени, с;

 – начальная фаза.

Мгновенные значения тока i, напряжения и или ЭДС е записываются в виде:

                                                                                                 (3.2)

                                                                                                (3.3)

                                                                                                   (3.4)

Аргумент синуса называется фазой. Угол  равен фазе в начальный момент времени t = 0 и поэтому называется начальной фазой.

Угловая частота  связана с периодом T и частотой f =1/T  формулами:

                                            или                                               (3.5)

Частота f, равная числу колебаний в 1с, измеряется в герцах (Гц). При f =50 Гц имеем = 314 рад/с.

С учетом (3.5) формула (3.1) может иметь вид:

                                                                                       (3.6)

На рисунке 3.1 изображены графики синусоидальных токов одинаковой частоты, но с различными амплитудами и начальными фазами:

По оси абсцисс отложено время t и величина, пропорциональная времени и измеряемая в радианах.

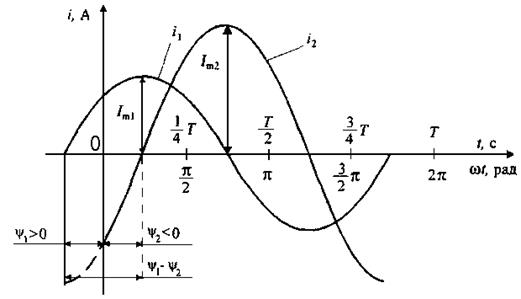
Рис. 3.1. График синусоидальных токов одинаковой частоты, но

с различными амплитудами и начальными фазами

Начальный фазный угол отсчитывается от начала синусоиды, т.е. от момента перехода синусоиды от отрицательных к положительным значениям до момента времени t = 0 (начало координат). При  начало синусоиды сдвинуто влево, а при – вправо от начала координат.

Если у нескольких синусоидальных функций, изменяющихся с одинаковой частотой, начала синусоид не совпадают, то говорят, что они сдвинуты друг относительно друга по фазе.

Сдвиг фаз измеряется их разностью, которая равна разности начальных фаз. На рисунке 3.1, т.е. ток i₁ опережает по фазе ток i₂ на угол  или, что то же самое, ток i₂ отстает по фазе от тока i₁ на угол .

Если у синусоидальных функций одной частоты одинаковые начальные фазы, то говорят, что они совпадают по фазе; если разность их фаз равна  то говорят, что они противоположны по фазе (в противофазе). И если разность их фаз равна  то говорят, что они находятся в квадратуре.

Наибольшее распространение в электротехнике получил синусоидальный ток частотой 50 Гц, которая принята за стандартную. В США, например, стандартной является частота f = 60 Гц.

Диапазон частот, применяемых на практике синусоидальных токов и напряжений, очень широк: от долей герца, например, в геологоразведке, до десятков тысяч мегагерц (МГц) в радиолокации.

Синусоидальные токи и напряжения низких частот (до нескольких килогерц) получают с помощью синхронных генераторов, в которых используется принцип получения синусоидального напряжения путем вращения витка с постоянной угловой скоростью в однородном магнитном поле. Этот принцип основан на явлении электромагнитной индукции, открытом в 1831 году М. Фарадеем. Синусоидальные токи и напряжения высоких частот (ВЧ) получают с помощью ламповых или полупроводниковых генераторов.

Источники синусоидальной ЭДС (источники синусоидального напряжения) показывают на схемах с помощью условных обозначений (рис. 3.2,а, б) или только указывают напряжение между зажимами источника (рис. 3.2,в), т.к. в большинстве случаев принимают источники идеальными и ввиду равенства нулю их внутреннего сопротивления имеем e = u, Ė = Ů и т.д.

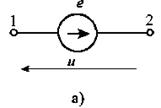
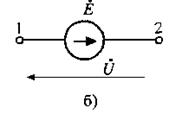
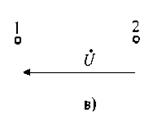
Рис. 3.2. Условные обозначения идеальных источников ЭДС

3.1.2 Действующее и среднее значения синусоидальных токов и напряжений. Согласно закону Джоуля–Ленца, тепловая энергия Q, выделяемая в резисторе с сопротивлением R при протекании по нему постоянного тока I₀ в течение промежутка времени t, равна:

                                                                                                      (3.7)

Для синусоидального тока формулу (3.7) можно применить лишь для определения тепловой энергии dQ, выделившейся в резисторе с сопротивлением R за бесконечно малый промежуток времени dt, в течение которого силу тока i можно считать не изменяющейся:

                                                                                                         (3.8)

За период времени Т выделившаяся энергия равна:

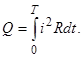                                                                                                           (3.9)

Пусть , тогда:

.

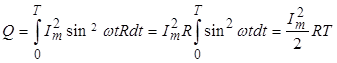Введем величину , называемую действующим значением синусоидального тока, и, подставив ее в последнее выражение, получим:

                                                                                                     (3.10)

Сопоставив формулу (3.10), полученную для синусоидального тока, с формулой (3.7), справедливой для постоянного тока, делаем вывод: Действующее значение синусоидального тока равно такому значению постоянного тока, который за один период выделяет в том же резисторе такое же количество тепла, как и синусоидальный ток.

Аналогично существуют понятия действующих значений синусоидальных напряжений и ЭДС:

                                                 и                                        (3.11)

Из формул (3.9) и (3.10) получаем:

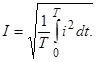                                                                                                 (3.12)

В силу (3.12) действующее значение синусоидального тока часто называют среднеквадратичным или эффективным значениями.

Действующие значения токов и напряжений показывают большинство электроизмерительных приборов (амперметров, вольтметров).

В действующих значениях указываются номинальные токи и напряжения в паспортах различных электроприборов и устройств.

Под средним значением синусоидального тока понимают его среднее значение за полупериод:

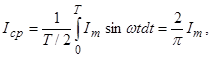                                                                        (3.13)

т.е. среднее значение синусоидального тока составляет от амплитудного значения. Аналогично,

3.1.3 Изображение синусоидальных токов, напряжений и ЭДС комплексными числами и векторами. Синусоидально изменяющийся ток i изображается комплексным числом:

                                                                     (3.14)

Принято изображение тока находить для момента времени t = 0:

                                                                                       (3.15)

Величину  называют комплексной амплитудой тока или комплексом амплитуды тока.

Под комплексом действующего значения тока или под комплексом тока  понимают частное от деления комплексной амплитуды тока на :

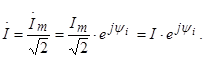                                                                         (3.16)

Под комплексами напряжения и ЭДС понимают подобные выражения

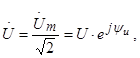
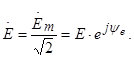
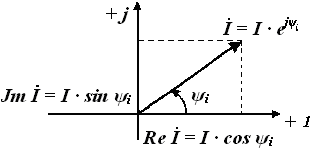
Рис. 3.3. Изображение синусоидального тока на комплексной плоскости вектором

Комплексы тока, напряжения и ЭДС изображаются также на комплексной плоскости векторами. Например, на рисунке 3.3 изображен вектор . При этом угол  отсчитывается от оси +1 против часовой стрелки, если . Из рисунка 3.3 следует, что комплекс тока  (так же, как комплекс напряжения и ЭДС) можно представить

а) вектором ;

б) комплексным числом в показательной, алгебраической и тригонометрической формах:

                                                         (3.17)

Пример 3.1 Ток . Записать выражение для комплексной амплитуды этого тока.

Решение. В данном случае  Следовательно,

Пример 3.2 Комплексная амплитуда тока . Записать выражение для мгновенного значения этого тока.

Решение. Для перехода от комплексной амплитуды к мгновенному значению надо умножить на  и взять коэффициент при мнимой части от полученного произведения:

Пример 3.3 Записать выражение комплекса действующего значения тока для примера 3.1.

Решение.                 

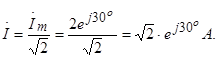
ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ

-      подвести итоги занятия;

-      напомнить тему, цели и учебные вопросы;

-      объявить оценки;

-      ответить на вопросы;

-      отметить активность и дисциплину на занятии;

-      дать задание на самоподготовку.

Список используемой литературы

Ванцов, В.И. Автомобильные эксплуатационные материалы [Электронный ресурс] : учебное пособие / В.И. Ванцов. - Рязань: ФГБОУ ВПО «Рязанский государственный агротехнологический университет имени П.А.Костычева», 2014. - 172 с.